智能网联环境下的混合动力汽车分层能量管理*

钱立军，邱利宏，2，司远，王金波

(1.合肥工业大学机械与汽车工程学院，合肥230009;2.克莱姆森大学国际汽车研究中心，美国格林维尔29607)

智能网联环境下的混合动力汽车分层能量管理*

钱立军1，邱利宏1，2，司远1，王金波1

(1.合肥工业大学机械与汽车工程学院，合肥230009;2.克莱姆森大学国际汽车研究中心，美国格林维尔29607)

为实现混合动力汽车的实时最优能量管理，提出一种基于智能网联的分层能量管理控制方法。上层控制器利用交通信号灯正时求解目标车速的范围，而采用快速模型预测控制(F-MPC)算法预测给定时间窗口内的最优目标车速序列。下层控制器根据最优目标车速序列，利用基于威兰斯线方法的等效燃油消耗最小策略(WLECMS)进行混合动力汽车能量管理。硬件在环试验结果表明，所提出的基于智能网联的上层控制器可避免混合动力汽车红灯停车，而F-MPC可实现与MPC相近的最优车速预测和燃油经济性，且每一时间步长的计算时间可缩短到MPC的7.2%;WL-ECMS可实现良好的车速跟随，百公里油耗与ECMS相当，且每一时间步长的计算时间可缩短到ECMS的1.48%。

智能网联汽车;混合动力汽车;分层控制;快速模型预测控制;能量管理

前言

混合动力汽车的能量管理控制方法直接影响整车的动力性、经济性、舒适性和排放，是混合动力汽车领域研究的重点和难点［1］。目前，已经实现产业化应用的是基于规则的控制方法，但这种控制方法依赖专家经验，不具备良好的工况适应性，因此，学者们重点研究了基于优化的控制方法。

基于优化的控制方法主要有全局优化和瞬时优化两类。在全局优化算法中，动态规划(dynamic programming，DP)、二次规划(quadratic programming，QP)和变分法(variational method，VP)等方法都需要已知循环工况，而在汽车实际行驶过程中，循环工况是未知的［2］。其中，动态规划算法基于逆向推理与正向优化相结合的贝尔曼原理，是搜索能力最好的全局优化算法，但程序结构十分复杂，且在线寻优需要采用模型预测(model predictive control，MPC)算法获取循环工况，增加了计算的时间成本，不满足实车应用的要求［3］。为节省程序运行的时间，学者们研究了基于极小值原理的瞬时优化算法，如等效燃油消耗最小策略(equivalent consumption minimization strategy，ECMS)和庞特亚金极小值原理(Pontryagin's minimum principl，PMP)等，这些算法无需已知循环工况即可获得近似的全局最优解［4］。然而，相对于汽车处理器的运算能力，这些算法依然无法实现实时控制［5］。

本文中提出一种基于智能网联［6］的混合动力汽车分层能量管理控制方法。上层控制器采用交通信号灯正时(signal phase and timing，SPAT)和快速模型预测控制(fast model predictive control，F-MPC)算法求解最优目标车速序列。下层控制器根据上层控制器的最优目标车速序列，采用基于Willans Line方法的等效燃油消耗最小策略(Willans Line equivalent consumption minimization strategy，WL-ECMS)进行混合动力汽车最优能量管理。

1 上层控制器的数学模型

本文中设计的分层控制系统中，上层控制器基于交通信号灯正时［7］计算目标车速的范围，基于快速模型预测算法，求解给定时间窗口的最优目标车速序列。

在汽车队列中，任意一辆混合动力汽车的纵向动力学模型［8－9］为

式中:vi为第i辆车的速度，m/s;ui为第i辆车的控制变量，含义为任意时刻单位质量牵引力或制动力，N/kg;Mi为第i辆车的质量，kg;CD为气动阻力系数; ρa为空气密度，kg/m3;Afi为第i辆车的迎风面积，m2;μ为滚动阻力系数;θ为坡度，(°)。假设θ很小，令cosθ=1，sinθ=θ。

本文中利用交通信号灯正时求解目标车速的范围，避免混合动力汽车红灯停车。目标车速范围的计算原理示意图如图1所示［10］。当下一路口为绿灯且满足最高行驶车速约束时，汽车可提高其行驶车速至不超过最大允许车速的最大可能值以保证在红灯到来之前经过某一交叉路口(此时得到的为车速上限);或者降低行驶车速保证经过交叉路口时该路口刚好由红灯变为下一个绿灯(此时得到的为车速下限)。当下一路口为红灯时，汽车须减速以保证在经过该路口时刚好由红灯变为绿灯(此时得到的为车速上限)或者在下一个绿灯结束之前经过该交叉路口(此时得到的为车速下限)。为了在尽可能避免红灯停车的基础上减少汽车行驶的时间，汽车目标车速的初始值一般设定为目标车速范围的上限。基于此原理，目标车速范围的下限和上限值［8］分别为

式中:vil为目标车速的下限，m/s;vih为目标车速的上限，m/s;dia(td)为第i辆车的位置si与交通信号灯a的距离，m;Kw为信号灯的循环次数，取整数;tr和tg分别为红灯和绿灯的持续时间，s;tc为一个红绿灯周期的时间，s;td为汽车行驶的时间，s;vimax为汽车行驶速度的最大值，m/s。

图1 车速范围计算原理示意图

2 基于快速模型预测的最优车速求解

本文中选取的最优车速预测目标函数为混合动力汽车单位距离油耗、前后车的相对距离、下层控制器的车速跟随和单位质量牵引力或者制动力等4个方面的加权值之和，如式(4)所示。该式输出的优化变量为混合动力汽车当前时刻的最优目标车速viobj和位置si。

式中:Sij为第i辆车和第j辆车的距离，m;viobj为目标车速，m/s;ωi(i=1，2，3，4)为权值系数;si(t)和sj(t)分别为第i辆车和第j辆车在时间t时的位置，用坐标表示;th为预先设定的前后两车的间隔时间，s;S0为预先设定的安全距离，m;vimin为汽车最低行车速度，m/s;n为车队中混合动力汽车的数量;T为给定的时间窗口，s。

在智能网联环境下，每辆车每隔时间T都发送该车的位置和目标车速信息到紧随其后的一辆车。当混合动力车当前时刻车速和位置均确定时，最优目标车速预测目标函数可采用模型预测求解。模型预测的求解算法一般采用序列二次规划(seqential quadratic programming，SQP)［6］，然而，基于序列二次规划的模型预测程序结构较为复杂，难以实现实时控制。为此，本文中针对控制算法的具体结构，设计快速模型预测［11－12］算法给定时间窗口T内的最优车速序列。

首先将式(4)所示的最优车速预测目标函数写成二次规划的形式:

式中:yi为包含目标车速和理想控制变量的状态变量;Qi为对角阵;yiobj为状态变量的目标值;Pi，qi，Ci和bi均为与状态变量相关的系数矩阵。

式(5)所示的二次规划问题，可以用式(6)所示的拉格朗日方程求解。

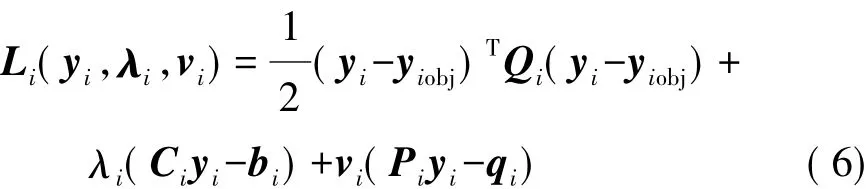
式中λi和νi为拉格朗日乘子。

拉格朗日方程的1阶库恩-塔克(KKT)最优条件为

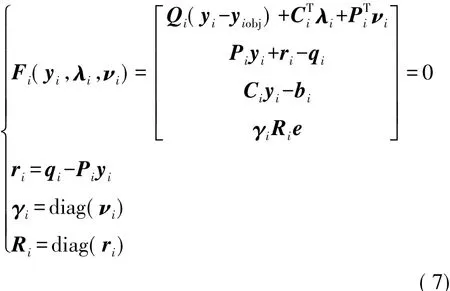
式中:ri为松弛变量;γi和Ri分别为拉格朗日乘子νi和松弛变量ri主对角线元素组成的列向量;e为单位列向量。

本文中采用牛顿迭代法求解1阶库恩－塔克最优条件方程，牛顿迭代法的迭代方程为

式中:［ΔyiΔλiΔνiΔri］T为所述牛顿迭代法优化变量的搜索方向;βi为迭代步长，该迭代步长可保证拉格朗日乘子和松弛变量为正值。

牛顿迭代法优化变量的搜索方向用式(9)求解。

式中Ryi，Rλi，Rυi和Rsi为所述库恩-塔克最优条件的残差。

由于式(9)所示方程组的线性相关性，可通过线性变化将其简化为线性无关的方程组:

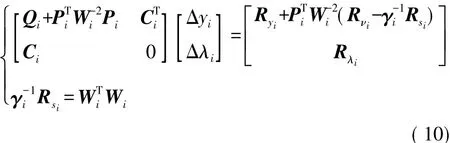
式中:［ΔyiΔλi］T为简化后的牛顿迭代法的搜索方向;Wi为与松弛变量相关的变换矩阵。

采用乔里斯基(Cholesky)因式分解法求解式(10)，因式分解后的方程组为

根据式(11)解出的最优状态变量yi和牛顿迭代法的迭代方程，即可预测给定时间窗口T内的最优目标车速序列。

理论研究表明，通过乔里斯基因式分解法求解简化后的方程组，使牛顿迭代法的计算速度由T(nx+nu)3浮点每秒提高到(1/3)T3(2nx+nu)3浮点每秒［12］。其中nx和nu分别为所述混合动力汽车的纵向动力学模型状态变量和控制变量的维数。

3 下层控制器的数学模型

本文中设计的下层控制器集成能量管理优化算法，利用接收到的驾驶员加速和制动信息，计算当前时刻动力部件的最优转矩或功率分配，然后将最优控制指令发送给动力部件控制器。各动力部件控制器根据控制指令控制动力部件执行相关操作，并将其实际输出反馈给下层控制器进行闭环修正。

为在保证实时控制的基础上实现混合动力汽车最优转矩分配，本文中采用一种基于Willans Line方法［13］的等效燃油消耗最小策略。

WL-ECMS的基本原理是在控制系统建模时，基于发动机和电机的Willans Line模型，将依赖于查表的参数近似规则化，从而将基于搜索的ECMS算法简化为与基于规则类似的算法，在保证近似最优解的前提下大大节省时间成本［14］。

发动机Willans Line模型为

式中:Pef为燃油功率，W;Pem为发动机输出的有效功率，W;ae和be为基于试验数据的回归系数。

电机的Willans Line模型为

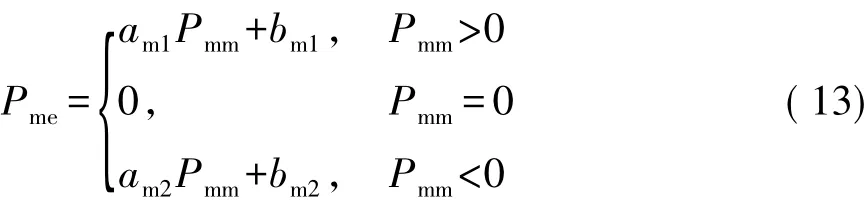
式中:Pme为电机消耗的功率，即电池功率，W;Pmm为电机输出的有效功率，W;am1和bm1为电机输出的有效功率大于零时基于试验时间的回归系数;am2和bm2为电机输出的有效功率小于零时基于试验时间的回归系数。

引入等效电压的概念，将动力电池消耗的能量用等效电压乘以电流等效为燃油的消耗。基于等效电压，ECMS策略可表示为

式中:Peq为混合动力汽车的等效功率，W;μ为决定动力电池单位电流等效功率的等效电压，V;Ibat为动力电池电流，A;λ为等效因子;Hg为燃油的热值，J/s。

本文中研究的混合动力汽车工作模式只有纯电动模式和混合动力模式。根据发动机和电机的Willans Line模型、基于动力电池内阻模型的电机功率消耗模型和混合动力汽车的功率平衡方程，可得到纯电动模式和混合动力模式混合动力汽车的等效功率的表达式。

纯电动模式下的等效功率为

式中:Peq－EV为纯电动模式的等效功率，W;Preq为混合动力汽车的需求功率，W;Uoc为动力电池的开路电压，V;Rbat为动力电池内阻，Ω;

纯电动模式下，混合动力汽车由电机单独驱动，故此时的等效功率即为电机的最优有效输出功率，此时发动机的有效输出功率为零。

混合动力模式的等效功率为

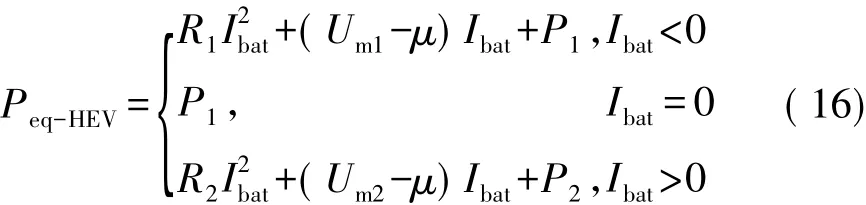
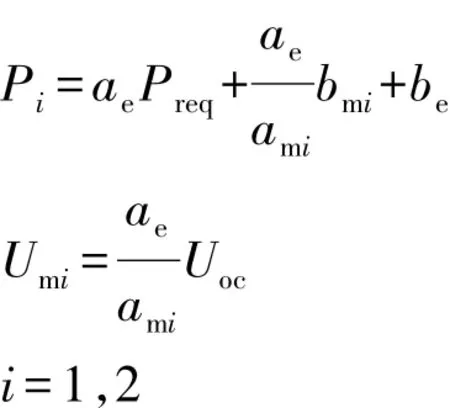
式中:Peq－HEV为混合动力模式的等效功率，W;Ri为与电池内阻相关的变量，Ω;Pi为与功率相关的变量，W;Umi为与动力电池开路电压相关的变量，V。

由式(16)可得到混合动力模式的最小等效功率的表达式:

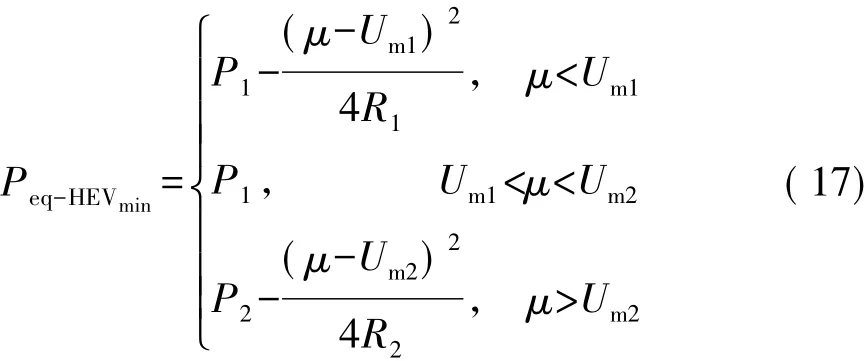
与混合动力模式最小等效功率对应的动力电池电流，即混合动力模式最优电流为

由此可知，混合动力模式最优的电机消耗功率为

因为混合动力汽车总的需求功率等于发动机和电机的有效输出功率之和，所以由式(12)、式(13)和式(19)即可得到混合动力模式下由Willans Line模型的回归参数表示的发动机和电机的最优输出功率和。

基于纯电动模式和混合动力模式下发动机和电机的最优输出功率，可将基于WL-ECMS的控制方法简化为与基于规则类似的形式:

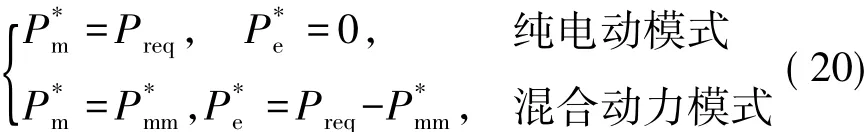
4 试验结果与分析

4.1 试验设置

采用美国克莱姆森大学的大型服务器Palmetto (本次试验采用计算模块为HP DL580，处理器为24核Intel Xeon7542，RAM为128G)计算上层控制器的最优目标车速，用于下层能量管理控制方法的硬件在环试验，试验台架如图2所示。本次硬件在环试验，发动机及与其同轴耦合的ISG电机为实物，其余部件均采用dSPACE模拟。采用dSPACE Micro-Autobox作为控制器原型，与主机连接;采用CLP1104 AD/DA板通过CAN总线连接Autobox与AVL试验台架，传输发动机和ISG电机控制指令并反馈其实际输出值至dSPACE仿真模型。将控制代码编译并下载到Autobox后，进行实时的硬件在环试验，试验时间设置为450s。

图2 硬件在环试验台架

在测试程序中，设置车队中有10辆同型号的混合动力车且都在同一条车道上运行;汽车的初始位置为［121 109 98 85 70 60 45.5666 30.2293 15.9196 0.8724］，单位为m;初始车速为［14.5 16 15 16.3 16.7 12.08 13.0047 14.1788 10.3730 12.0473］，单位为m/s;模型预测的时间窗口为6s，计算的步长为0.5s;设置信号灯数量为15，红灯持续时间为40s，绿灯持续时间为15s，两个交通信号灯的距离为500m;设置汽车的最大、最小车速分别为20m/s和0。设置每辆车的整车整备质量为1 750kg，迎风面积为2.36m2，空气阻力系数为0.32，滚动阻力系数为0.015，道路坡度为0，发动机功率为103kW，电机的额定功率为40kW，峰值功率为80kW。设置

4.2 仿真与试验结果

图3～图12分别为10辆混合动力汽车的车速曲线对比图，包含上层控制器采用F-MPC和MPC的最优车速和上层控制为F-MPC、下层控制器为WL-ECMS时的车速跟随曲线。由图可见，采用FMPC的上层控制器最优预测车速与采用MPC的最优预测车速大致相同，从而验证了本文中的上层控制方法控制效果良好。另外，对于一个时间步长，当式(4)上层控制器的MPC目标函数采用本文中提出的F-MPC求解算法时，其计算时间成本大幅度降低，仅为基于序列二次规划［6］求解时的7.2%。验证了本文中提出的F-MPC可在大幅缩短计算时间、实现实时控制的基础上实现与MPC相近的控制效果。由下层控制器的车速跟随曲线可知，基于WL-ECMS的下层控制器的跟随车速与上层控制器的最优预测车速基本一致，说明基于WL-ECMS的下层控制器可以保证良好的车速跟随，实现混合动力汽车基本的能量管理。

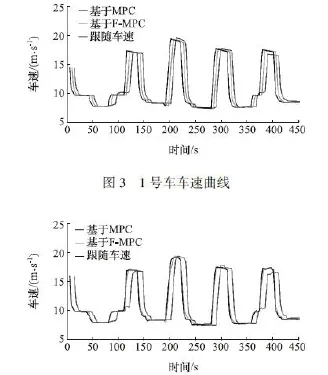
图42号车车速曲线

图13 ～图22分别为10辆混合动力汽车分别在WL-ECMS、ECMS和基于规则的下层能量管理控制方法下的SOC曲线。由图可见，在3种不同的下层控制方法下，动力电池SOC的波动范围始终保持在

图86 号车车速曲线

合理的范围内，说明3种下层能量管理控制方法均能实现混合动力汽车动力电池的均衡。对比不同的下层控制方法下的SOC曲线可知，当下层控制方法依次为基于规则、基于WL-ECMS、基于ECMS时，动力电池SOC波动范围依次减小，当下层控制方法依次为WL-ECMS和基于ECMS时，SOC的波动范围相当。说明基于WL-ECMS的下层控制方法可以实现与基于ECMS相当的能量均衡控制效果，且二者的控制效果均优于基于规则的控制方法。此外，对于一个时间步长，相对计算时间降低到基于ECMS的1.48%，计算时间成本大幅度降低。

图1210 号车车速曲线

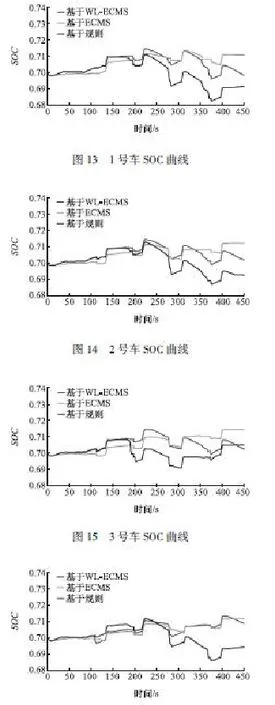
图164号车SOC曲线

图23 为本文中提出的基于智能网联的混合动力汽车的运动曲线。图中，与横轴平行的实横线表示红灯时间窗口，两个红灯时间窗口中间的空白区域表示绿灯时间窗口。由图可见，在本文中设定的试验方案下，混合动力汽车经过交通信号灯时遇到的均为绿灯。因此，本文中提出的车联网的上层控制器可有效避免混合动力汽车红灯停车。

图208 号车SOC曲线

表1为10辆混合动力汽车在不同上层和下层控制方法下的百公里油耗。由表可见:当上层控制器采用F-MPC或MPC时，下层控制器基于WL-ECMS的平均百公里油耗仅比基于ECMS的升高2.26%或3.57%;当下层控制器采用WL-ECMS或者ECMS时，上层控制器基于F-MPC的平均百公里油耗仅比基于MPC的升高0.96%或2.25%。

图23 基于智能网联的混合动力汽车曲线

5 结论

(1)上层控制器基于F-MPC与基于MPC得到的最优车速曲线基本保持一致。对于一个时间步长，程序的计算时间降低到MPC的7.2%，且上层控制器采用F-MPC与采用MPC时的百公里油耗相差较小。

(2)下层控制器采用WL-ECMS时动力电池SOC波动在合理的范围内，车速跟随误差较小，百公里油耗接近基于ECMS的百公里油耗。

(3)对于一个时间步长，基于WL-ECMS下层能量管理控制方法的计算时间降低到ECMS的1.48%。

(4)采用基于车联网的控制方法求解最优目标车速，混合动力汽车在经过交通信号灯时可以有效的避免红灯停车。

［1］钱立军，邱利宏，辛付龙，等．插电式四驱混合动力汽车能量管理与转矩协调控制策略［J］．农业工程学报，2014，30(19):55－64．

［2］LI Liang，YANG Chao，ZHANG Yahui．Correctional DP-based energy management strategy of plug-in hybrid electric bus for citybus-route［J］．IEEE Transactions on Vehicular Technology，2015，64(7):2792－2803．

［3］MOURA S J，FATHY H K，CALLAWAY D S，et al．A stochastic optimal control approach for power management in plug-in hybrid electric vehicles［J］．IEEE Transactions on Control System Technology，2011，19(3):545－555．

［4］LAURENT T，OLIVER G，CAROLE Q，et al．Energy management strategy and optimal hybridization level for a diesel HEV［J］．SAE International Journal of Alternative Powertrains，2012，1(1):260－271．

［5］ZAHER M H，CETINKUNT S．Real time energy management strategy for hybrid electric powertrains［C］．SAE Paper 2013－01－2396．

［6］LIN R，HOMCHAUDHURI B，PISU P．Fuel efficient control strategies for connected hybrid electric vehicles in urban roads［C］．ASME Dynamic Systems and Control Conference，Columbus，Ohio，USA，2015:77－83．

［7］MAHLER G，VAHIDI A．An optimal velocity-planning scheme for vehicle energy efficiency through probabilistic prediction of trafficsignal timing［J］．IEEE Transactions on Intelligent Transportation System，2014，15(6):2516－2523．

［8］HOMCHAUDHURI B，VAHIDI A，PISU P．A fuel economic model predictive control for a group of connected vehicles in urban roads［C］．American control conference，Chicago，Illinois，USA，2015:2741－2746．

［9］KAMAL M S，MUKAI M，MURATA J，et al．Model predictive control of vehicles on urban roads for improved fuel economy［J］．IEEE Transactions on Control System Technology，2013，21(3): 831－841．

［10］ASADI B，VAHIDI A．Predictive cruise control:Utilizing upcoming traffic signal information for improving fuel economy and reducing trip time［J］．IEEE Transactions on Control Systems Technology，2011，19(3):707－714．

［11］FEKRI S，ASSADIAN F．Fast model predictive control and its application to energy management of hybrid electric vehicles［M］．INTEC Open Access Publisher，2011:1－28．

［12］WANG Y，BOYD S．Fast model predictive control using online optimization［J］．IEEE Transactions on Control Systems Technolgy，2010，18(2):267－278．

［13］WEI X，GUZZELLA L，UTKIN V I，et al．Model-based fuel optimal control of hybrid electric vehicle using variable structure control systems［J］．ASME Journal of Dynamic Systems，Measurement，and Control，2007，129(1):13－19．

［14］YE X，JIN Z，HU X，et al．Design and implementation of a realtime power management strategy for a parallel hybrid electric bus［J］．Journal of Automotive Engineering，2014，228(13):1581－1598．

Hierarchical Energy Management of Hybrid Electric Vehicles Under the Environment of Intelligent and Connected Vehicles

Qian Lijun1，Qiu Lihong1，2，Si Yuan1＆Wang Jinbo1
1.School of Mechanical and Automotive Engineering，Hefei University of Technology，Hefei230009; 2.Clemson University International Center for Automotive Research，Greenville 29607，United States

In order to realize the real-time optimal energy management of hybrid electric vehicles(HEVs)，a hierarchical energy management control scheme based on intelligent and connected vehicle technology is put forward．The upper layer controller utilizes traffic signal phase and timing to obtain the target speed range，and uses fast model predictive control(F-MPC)algorithm to predict the optimal target speed sequences over a given time window．According to the optimal target speed sequences，the lower layer controller utilizes Willans-Line-based equivalent consumption minimization strategy(WL-ECMS)to fulfill the energy management of HEVs．The results of hardware-in-the-loop test show that with the intelligent and connected vehicle-based upper layer controller，HEVs can avoid red light stopping．The fuel economy with F-MPC is approximate to that of MPC and the calculation time for a single time step with F-MPC is reduced to 7.2%of that with MPC．WL-ECMS strategy can realize good speed tracking，its fuel economy is comparable with ECMS，and its calculation time for a single step is reduced to only 1.48%of that with ECMS．

intelligent and connected vehicles;HEVs;hierarchical control;fast model predictive control;energy management

10．19562/j．chinasae．qcgc．2017．06．003

*2012年国家新能源汽车技术创新工程(财建［2012］1095号)和2013年国家科技支撑计划课题专项资金(2013BAG08B01)资助。

原稿收到日期为2016年3月11日，修改稿收到日期为2016年8月11日。

邱利宏，博士，E-mail:qiulihong99@163．com。