浅谈数学解题后反思教学的几点体会

丁丁

【摘要】 数学离不开解题，但是数学学习的目的不是为了解题，而是为了学会解题。学生在解题过程中投入了大量的时间和精力，然而效果并不理想，究其主要原因是缺乏对解题活动进行反思。在新课标改革的背景下，反思作为一种能力，已经越来越被人们认识到它对学习的促进和发展带来的作用。学生通过解题后反思，能拓宽思路，优化解法，促进知识点之间的迁移，从而提高学习效率，增强分析解决问题的能力和多种思维能力。

【关键词】 反思 思维构建 能力提升

【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711（2017）05-078-01

0

中学数学课程标准中要求学生通过对解决问题过程的反思，获得解决问题的经验，从而不断地经历反思与构建思维的过程，彰显了对反思学习的重视。教师讲解后的反思是指讲解者对自身解题活动的深层次的反向思考，而作为学生，不仅是对解题的一般性的回顾或重复，更为重要的是深究解题过程中所涉及的知识、方法、思路及解题策略等，从而提高学习效率，增强多种思维能力，达到解题能力的提升。所以解题后的反思就显得尤为重要，那么解题后如何进行反思呢？我在近几年的九年级毕业班教学积累了一些经验与感悟，愿与大家共享。

一、反思解题方法，训练学生的发散思维能力

2017新课标新中考《浙江中考》第二课整式及其运算中有下面一道题目：

已知實数m，n满足m-n2=1，则代数式m2+2n2+4m-1的最小值为______。

解析：∵m-n2=1，∴n2=m-1，∴原式=m2+2m-2+4m-1=m2+6m+9-12=

（m+3）2-12≥-12，即代数式m2+2n2+4m-1的最小值为-12。明显，答案的解析过程是有偏差的。当m=-3时，代数式取到最小值-12，而在实数范围内，不存在n的值使得m=-3。换句话说，当m=-3时，n2=-4，n无实数解。

正确解法∵m-n2=1，∴n2=m-1，∵n2≥0，∴m-1≥0，m≥1.y=m2+2n2+4m-1

y=（m+3）2-12.（m≥1）由二次函数图像的性质可知，当m>-3时，y随着m的增大而增大，∴当m=1时，ymin=4.即m2+2n2+4m-1的最小值为4.

反思解题过程，其实这是一道求解代数式的最值问题，代数式本身的取值大小由变量决定，而在求解实际问题中，往往变量本身存在取值范围的限制，而函数能够很好的帮助我们研究变量之间的关系。从函数本身的性质出发，结合变量的取值范围，就能很好的避免错误的发生。

二、反思解题规律，促进学生的解题多样性

我们一起来看下面一道题：

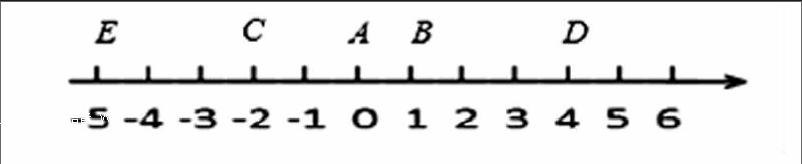
如图，点A的初始位置位于数轴上的原点，现对点A做如下移动：第1次从原点向右移动1个单位长度至点B，第2次从点B向左移动3个单位长度至点C，第3次从点C向右移动6个单位长度至点D，第4次从点D向左移动9个单位长度至点E……依次类推，这样至少移动___次后该点到原点的距离不小于41.

解析：根据坐标的变化：移动（2n-1）次后该点到原点的距离为3n-2，移动2n次后该点到原点的距离为3n-1.

（当3n-2≥4时，3n-2≥41时，n≥4313.

∵n是正整数，∴的最小值为15，此时移动了29次。

（当3n-1≥41时，n≥14.

∵n是正整数，∴n的最小值为14，此时移动了28次。

综上所述，至少移动28次后该点到原点的距离不小于41.

反思解题过程，这是有关动点变化，找规律的一道题目。按照一般的解题过程，通过表示动点的通式来确定动点的位置，从而解决移动次数是较为困难的。在课堂讲解过程中，也出现重复讲解仍然有学生不能理解的情况。其实找规律的题目不光可以从事物的变化过程入手，寻求一般的通式解决问题，更多时候可以从结果出发，观察结论而得出规律，可能会达到事半功倍的效果。

在课后的学生纠错本记录反思中，我发现了学生另外一种解法：移动1次对应数字为1，移动2次对应数字为-2，移动3次对应数字为4，移动4次对应数字为-5，移动5次对应数字为7……那么该点到原点的距离不小于41，等同于这个动点代表的数字的绝对值不小于41。从结果的绝对值来看，数字的排列中间缺3的倍数，41÷3=13……2，对应中间少了13个数字，所以只需移动28次即可。学生的题后反思给了我很多思考，用固定模式讲解题目过程确实有必要，但过分强调“套路”可能未必是最佳的应对策略。而反思解题规律，可能会对解题带来更多样性的选择。

三、反思解题差异，促进思维的深入

（2016.无锡）如图，已知OABC的顶点A，C分别在直线x=1和直线x=4上， O是坐标原点，则对角线OB长的最小值为_______。

解析：当点B在x轴上时，对角线OB的长最小，直线x=1与x轴交于点D，直线x=4与x轴交于点E.根据题意得∠ADO=∠CEB=90°，OD=1，OE=4.

∵四边形ABCD是平行四边形，

∴OA//BC，OA=BC，

∴∠AOD=∠CBE.

在ΔAOD和ΔCBE中，

∠AOD=∠CBE，

∠ADO=∠CEB，

OA=BC，

∴ΔAODΔCBE（AAS）.

∴BE=OD=1.

∴OB=OE+BE=5.

在解题过程中，参考教辅用书上的解法和网上中考解析大体相同。但在讲解过程中，学生始终对当点B在x轴上时，对角线OB的长最小有所困惑。在布置课后纠错作业时，学生提出另外的想法使我眼前一亮。

解法二：连接AC，与OB相交于点E，由平行四边形的对角线互相平分， AE=CE我们可以发现点E在直线x=512上，而OE=112OB，所求线段OB的最小值其实就可以转化成求解OE的最小值，当OE垂直于直线x=512时，线段OE最小为512，此时OB的值为5.

反观学生解题后的反思，其实我们可以发现，几何图形具有自身特有的性质，在解题过程中，我们往往会忽略这些性质。如果解题之后进行反思，感受解题的差异性，不仅提高了解题的技巧，更能够促进思维的深入。

学生在解题中运用自己的知识结构对问题进行审验，研究、寻找解决问题的思维策略，直到形成程序化的解决方案，这固然是我们教学的重点，但解题之后，如何反思知识结构的系统性，对解题过程进行纵向深入的探究，以及能否加强知识的横向联系，把问题所蕴含孤立的知识“点”扩展到系统的知识“面”将显得更为重要。学会解题后如何进行反思，就是将获得的知识通过再现、联系、整合以及在实际中的应用，以达到举一反三、触类旁通、熟练掌握、灵活应用的要求，把其意思引申一下，我们就不难理解为什么解题之后要进行反思了。

[ 参 考 文 献 ]

[1]任瑞芬.怎样进行解题后反思[J].软件：电子版，2015（1）.

[2]王天波.浅谈中学数学解题后反思的几点看法[J].东方教育，2015（4）.

[3]王芳琴.如何引导学生进行解题后反思[J].中学数学教学参考，2015（5X）.

[4]王怡.如何进行数学解题反思[J].数学学习与研究，2014（2）.