高压下P4/mmm结构Fe3Co晶态合金的磁性研究

张 辉， 成泰民， 禹国梁， 徐 策

(沈阳化工大学 材料科学与工程学院， 辽宁 沈阳 110142)

高压下P4/mmm结构Fe3Co晶态合金的磁性研究

张 辉， 成泰民， 禹国梁， 徐 策

(沈阳化工大学 材料科学与工程学院， 辽宁 沈阳 110142)

有序晶态合金Fe3Co处于一种特殊的磁临界状态，这种磁临界状态下体系的磁性对压力极为敏感.基于密度泛函理论第一性原理的投影缀加平面波方法(PAW)研究P4/mmm结构晶态合金Fe3Co的磁矩和电子结构随压力的变化规律.在压力为150 GPa附近出现了考虑电子自旋极化体系相对于不考虑电子自旋极化体系的相对焓差急剧下落后回升的现象，这与Fe2原子与Fe1原子对体系磁矩贡献发生变化的压力区间相对应，说明在150 GPa附近体系的微观磁结构对压力非常敏感，而且体系的基态结构处于不稳定状态.在压力大于700 GPa小于800 GPa区间内，体系的总磁矩线性显著减小，Fe3Co晶态合金的铁磁性坍塌临界压力为850 GPa.

铁磁性坍塌； 临界压力； 电子自旋极化； 电子比热系数； 第一性原理

1 计算方法

计算采用了基于密度泛函理论的平面波赝势方法的VASP[7-9]程序.电子间的交换关联作用选择基于广义梯度近似(GGA)的Perdew-Burke-Ernzerhof(PBE)[10]形式，离子实和价电子之间的相互作用采用投影缀加平面波[11](PAW) 方法计算，Fe 原子的价电子电子组态为3p64s13d7和Co原子的价电子电子组态为4s13p63d8.布里渊区积分采用monkhorst-pack方法对布里渊区进行采样，积分网格为9×9×13，平面波基函数的截断能量取为600 eV.对原子的弛豫采用一阶的methfessel-paxton smearing方法，smearing展宽为0.2 eV，总能的计算采用了BlÖCHL[12]修正的线性四面体方法以获得更高的精度[13].电子和离子弛豫的自洽收敛标准分别为能量小于1.0×10-6eV 和1.0×10-4eV.对空间群为P4/mmm的Fe3Co的晶态合金进行了结构优化并与文献[14]报道的结构进行了对比(见表1和图1)，结果表明我们的计算结果是可靠的.

表1 有序晶态合金Fe3Co的晶体结构、晶格常数、原子位置和磁矩

图1 有序晶态合金Fe3Co的晶体结构

2 结果与讨论

2.1 高压下有序晶态合金Fe3Co的磁矩

从图2(a)可知：在压力小于150 GPa时，Fe2原子对体系(P4/mmm结构的有序晶态合金Fe3Co)磁矩的贡献最大，其次为Fe1原子，Co原子的贡献最小，在此压力区体系的总磁矩线性减小，但在150 GPa附近体系的磁矩急剧减小；压力在大于150 GPa小于700 GPa区间内，Fe1原子的磁矩对体系磁矩的贡献最大，其次为Fe2原子的贡献，Co原子对体系的贡献最小，在此压力区体系的总磁矩缓慢减小；在压力大于700 GPa小于800 GPa区间内，体系的总磁矩线性显著减小；在800 GPa至850 GPa附近，体系的铁磁性完全坍塌，因此，P4/mmm结构的有序晶态合金Fe3Co的铁磁性坍塌临界压力处于此压力区间.由图2(b)可知：体系的磁矩主要由3d电子的贡献引起的，且3d电子对磁矩的贡献大于体系的总磁矩，这说明4s电子与3p电子对体系的磁矩贡献为抗磁性的；在小于150 GPa压力区间内，体系的磁矩线性减小，这与3d电子直接相关，且3d电子的贡献也在150 GPa附近减小，但是4s和3p电子的贡献几乎不变；体系的铁磁性坍塌与3d电子的自旋极化坍塌密切相关，体系铁磁性坍塌临界压力处于850 GPa附近.

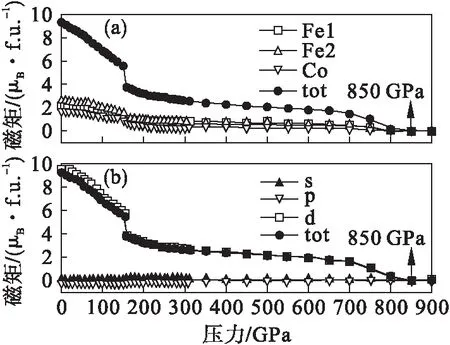
图2 不等价原子(a)、不同轨道电子(b)对体系磁矩的贡献和总磁矩

2.2 高压下有序晶态合金Fe3Co的相对焓差及电子比热系数

计算过程中所施加的压力均为等效静水压力，不改变晶态合金Fe3Co的晶格对称性.由图3可知：压力小于34 GPa时，考虑电子自旋极化(考虑磁性)时，P4/mmm结构的Fe3Co合金基态结构稳定.在压力为150 GPa附近出现了考虑电子自旋极化的体系相对于不考虑电子自旋极化的体系的相对焓差急剧下落后回升的现象，这与Fe2原子与Fe1原子对体系磁矩贡献发生变化的压力区间相对应，说明在150 GPa附近体系的磁结构对压力非常敏感，而且体系的基态结构处于不稳定状态.

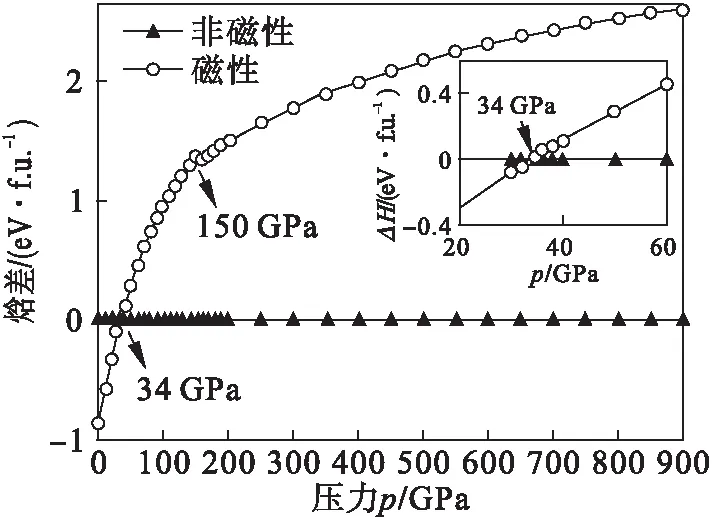
图3 有序晶态合金Fe3Co的焓差随压力的变化

由图4可知：晶态合金Fe3Co的电子比热系数也在150 GPa压力区间振荡且振幅较大.二元合金的基态结构稳定性与电子比热系数关联(参见文献[4-6]),再一次说明在此压力区间体系的基态结构不稳定.

图4 有序晶态合金Fe3Co的电子比热系数随压力的变化

2.3 高压下有序晶态合金Fe3Co的电子结构

不同压力下有序晶态合金Fe3Co的电子态密度如图5所示.

图5 0～300 GPa压力下有序晶态合金Fe3Co的电子态密度

由图5可知：在常压下，P4/mmm结构的Fe3Co晶态合金体系的电子自旋极化主要由Fe原子和Co原子的3d电子贡献的，其中，单个Fe2原子的贡献大于单个Fe1原子的贡献，这是因为在晶体场的作用下3d电子处于高自旋态，Co原子的3d电子处于低自旋态，因此,不等价的Fe1原子与Fe2原子的磁矩大于Co原子的磁矩；随着压力的增大，体系的电子自旋极化减小，特别是在150 GPa附近，体系的电子自旋极化急剧减弱，表现为自旋朝上的电子态密度与自旋朝下的电子态密度分布趋于对称;随着压力的增大，费米能级处的电子态密度N(EF)逐渐增大，在150 GPa附近N(EF)急剧增大，这说明随着压力的增大体系的3d价电子对体系比热的贡献逐渐增大，且150 GPa附近N(EF)急剧增大.

由图6可知：空间群为P4/mmm结构的Fe3Co晶态合金的铁磁性坍塌临界压力处于850 GPa附近，与图2结果相符；随着压力的增大，空穴区(高能区)Co原子对体系电子态密度的贡献逐渐增大，且在费米能级以下自旋朝上及自旋朝下的电子态密度趋于对称，Fe原子的3d价电子态密度的峰值向费米能级处移动.由图2、图5和图6可知：Fe1原子、Fe2原子、Co原子的4s电子与3p电子对体系磁矩的贡献很小，且3p电子因处于满带，其贡献表现为抗磁性显著.

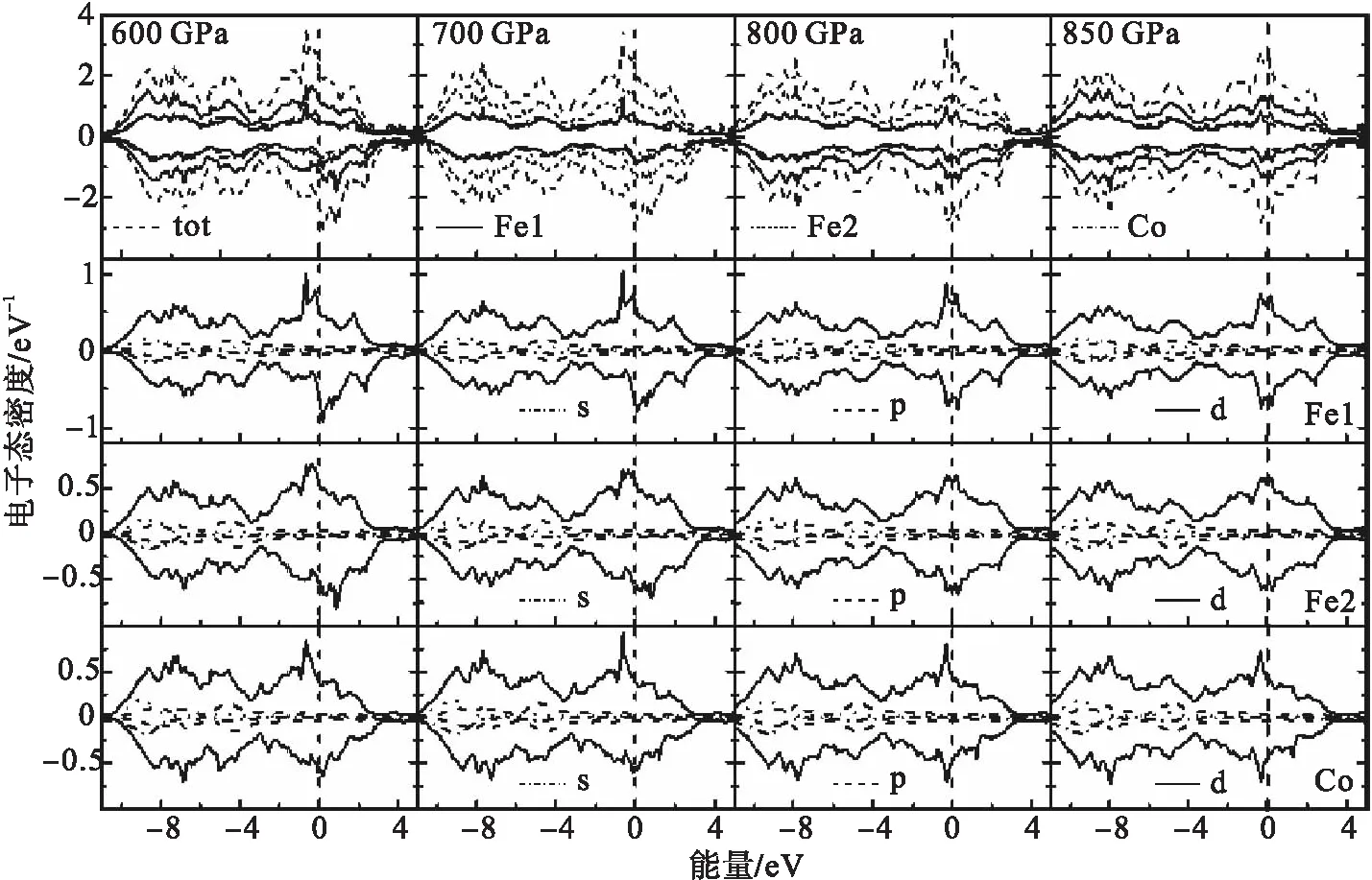
图6 600～850 GPa压力下有序晶态合金Fe3Co的电子态密度

3 结 论

利用第一性原理计算压力诱导下有序晶态合金Fe3Co的磁性及电子结构，得到如下结论：

(1) 在常压下，P4/mmm结构的Fe3Co晶态合金体系的电子自旋极化主要由Fe原子和Co原子的3d电子贡献的.随着压力的增大，体系的3d价电子对体系的电子比热的贡献逐渐增大，特别是在150 GPa附近急剧增大且出现了振荡现象，说明在150 GPa附近体系的磁结构对压力非常敏感，而且体系的基态结构处于不稳定状态.

(2) 随着压力的增大，有序晶态合金Fe3Co体系中的总磁矩不断减少，使得总的极化电子态密度不断减少，Fe原子的3d价电子态密度的峰值向费米能级处移动.在压力小于150 GPa时，Fe2原子对体系(P4/mmm结构的有序晶态合金Fe3Co)磁矩的贡献最大，其次为Fe1原子，Co原子的贡献最小.当压力在大于150 GPa小于700 GPa区间内，Fe1原子的磁矩对体系磁矩的贡献最大，其次为Fe2原子的贡献，Co原子对体系的贡献最小，在此压力区体系的总磁矩缓慢减小.在压力大于700 GPa小于800 GPa区间内，体系的总磁矩线性显著减小，Fe3Co晶态合金的铁磁性坍塌临界压力为850 GPa.Fe3Co晶态合金的铁磁性坍塌与3d电子的自旋极化坍塌密切相关.

[1] 周磊,金自力,张羊换,等.铁钴基软磁材料合金化的研究进展[J].金属功能材料,2006,13(6):37-41.

[2] 成泰民,孙腾,张龙燕,等.高压下γ′-Fe4N晶态合金的声子稳定性与磁性[J].物理学报,2015,64(15):156301-1-156301-10

[3] 成泰民,张龙燕,孙腾,等.高压下有序晶态合金Fe3Pt的低能声子不稳定性及磁性反常[J].物理学报,2015,64(14):146301-1-146301-11

[4] XU J H,OGUCHI T,FREEMAN A J.Crystal Structure,Phase Stability,and Magnetism in Ni3V[J].Physical Review B,1987,35(13):6940-6943.

[5] RAVINDRAN P,ASOKAMANI R.Electronic Structure,Phase Stability,Equation of State,and Pressure-dependent Superconducting Properties of Zr3Al[J].Physical Review B,1994,50(2):668-678.

[6] RAVINDRAN P,SUBRAMONIAM G,ASOKAMANI R.Ground-state Properties and Relative Stability Between The L12 and DoaPhases of Ni3Al By Nb Substitution[J].Physical Review B,1996,53(3):1129-1137.

[7] KRESSE G,FURTHMÜLLER J.Efficient Iterative Schemes for Ab Initio Total-energy Calculations Using A Plane-wave Basis Set[J].Physical Review B,1996,54(16):11169-11186.

[8] KRESSE G,FURTHMÜLLER J.Efficiency of Ab-initio Total Energy Calculations for Metals and Semiconductors Using A Plane-wave Basis Set[J].Computational Materials Science,1996,6(1):15-50.

[9] KRESSE G,JOUBERT D.From Ultrasoft Pseudopotentials to the Projector Augmented-wave Method[J].Physical Review B,1999,59(3):1758-1775.

[10]PERDEW J P,BURKE K,ERNZERHOF M.Generalized Gradient Approximation Made Simple[J].Physical Review Letters,1996,77(18):3865-3868.

[11]KRESSE G,HAFNER J.Ab Initio Molecular Dynamics for Liquid Metals[J].Physical Review B,1993,47(1):558-561.

[12]BLÖCHL P E.Projector Augmented-wave Method[J].Physical Review B,1994,50(24):17953-17979.

[13]禹国梁，成泰民，张辉，等.高压下L10-FePd晶态合金的物性研究[J].沈阳化工大学学报，2017，31(1)：91-96.

Study on the Magnetism of P4/mmm Fe3Co Crystalline Alloy at High Pressure

ZHANG Hui， CHENG Tai-min， YU Guo-liang， XU Ce

(Shenyang University of Chemical Technology， Shenyang 110142， China)

The ordered crystalline alloy Fe3Co is a kind of special magnetic critical state,in which the magnetism of system is extremely sensitive to pressure.Using projector-augmented wave method based on density functional theory,we calculate the dependence of magnetic moment and electronic structure of crystalline alloy P4/mmm-Fe3Co on external pressure.The enthalpy difference of system with electronic spin polarization being considered or not fluctuates dramatically near 150 GPa,which corresponds to the contribution of Fe1 and Fe2 atoms to the magnetic moment.It shows that the magnetic microstructure is extremely sensitive to pressure,as well as the ground-state structure is instable.When the pressure ranges from 700 GPa to 800 GPa,the total magnetic moment decreases linearly.The ferromagnetic collapse critical pressure of Fe3Co crystalline alloy is 850 GPa.

ferromagnetic collapse; critical pressure; electronic spin polarization; electronic specific heat coefficient; first principle

2016-11-16

国家自然科学基金面上项目(11374215)

张辉(1990-)，男，黑龙江齐齐哈尔人，硕士研究生在读，主要从事磁性物理及材料物性的研究.

成泰民(1970-)，男，辽宁沈阳人，教授，博士，主要从事磁学及磁性材料物性的研究.

2095-2198(2017)02-0188-05

10.3969/j.issn.2095-2198.2017.02.019

O521+.2

： A