基于磁致伸缩作动器的拉索主动控制时滞补偿研究

孙洪鑫， 李建强， 王修勇， 方 聪

(湖南科技大学 土木工程学院， 湖南 湘潭 411201)

基于磁致伸缩作动器的拉索主动控制时滞补偿研究

孙洪鑫， 李建强， 王修勇， 方 聪

(湖南科技大学 土木工程学院， 湖南 湘潭 411201)

拉索的大幅振动给斜拉桥安全运营带来威胁，采用磁致伸缩作动器施加轴向控制力抑制拉索横向振动是一种可行的方法，由于控制系统时滞的存在，会影响拉索控制效果和结构的稳定性。建立了磁致伸缩作动器动力学模型和拉索-磁致伸缩作动器面内控制系统方程，提出了基于移相法的拉索控制时滞补偿理论和拉索非线性控制系统的线性化方法，通过仿真分析得到了拉索振动控制时滞补偿效果。研究表明，在拉索-磁致伸缩作动器时滞控制系统中，移相法能够取得良好的时滞补偿效果，接近无时滞最优控制减振率。

拉索；磁致伸缩作动器；时滞补偿；移相法；仿真分析

斜拉索是具有初应力的柔性结构,在使用状态过程中由于环境激励(风、雨、结构振动、汽车荷载)的作用,会产生各种形式的有害振动。现有拉索振动控制的方法包括设置辅助索、改变拉索气动特性、安装阻尼器、主动与半主动控制等。针对拉索主动控制，一些学者也做了大量的研究，Yamaguchi等[1]提出了通过直接施加横向力来控制拉索振动，但在横向施力点会产生弯曲应力，会导致拉索疲劳问题；Fujino等[2-5]通过压电作动器在拉索锚固端施加沿拉索轴向控制力来控制拉索的振动，并开展了试验研究；Gattulli等[6]同样也采用压电作动器在拉索锚固端施加轴向控制力来控制拉索振动，提出了多点优化控制的方法，并进行了仿真和试验研究；周海俊等[7]采用智能材料形状记忆合金来提供轴向控制力，对斜拉索风雨振控制方面进行了仿真研究；朱保兵等[8]对不同边界条件下拉索振动的主动控制开展了研究；王修勇等[9]研究了采用磁致伸缩材料来提供轴向作动力、进行了拉索主动控制与半主动控制仿真研究。虽然振动控制技术已经应用于工程实际并取得一定成效，但主动控制过程中时滞问题研究较少。时滞是结构振动控制系统中普遍存在的现象，从信号采集处理、控制律运算、信号传输到作动器响应等都需要一定的时间。已有研究表明：时滞对控制系统的性能有很大的影响，它使控制系统的控制效果变差，稳定性降低，甚至导致控制系统失稳[10-11]。因此如何减小甚至消除时滞产生的影响成为结构振动控制不可避免的实际问题[12]。在时滞补偿控制方面，Abdel-Rohman[13]提出了Taylor级数展开法，该方法将时滞微分方程的时滞项按Taylor级数进行展开，在时滞量比较小的情况下，对结构时滞补偿情况较好；Mc Greery等[14]基于Taylor级数提出了状态预估法，但控制时滞量不能过大，且状态预估法的效率依赖于所估计状态的精度；Chung等[15]最早提出了移相法，该方法是通过补偿矩阵对增益矩阵的修正来补偿时滞对控制效果的影响，理论与试验证明都能够很好地补偿结构存在的时滞情况；周岱等[16]提出了基于神经网络的时滞补偿算法，该方法主要是利用神经网络方法结合状态预测补偿法,对大跨空间结构风振响应进行时滞补偿控制；薛晓敏等[17]提出基于遗传算法的结构振动时滞补偿算法，通过遗传算法对增益矩阵的修正来补偿时滞的影响。

磁致伸缩材料是一种智能功能材料，Reed[18]设计了磁致伸缩作动器，开展了大型设备主动隔振研究；Caraman等[19]开展了作动器的非线性研究，建立了材料的非线性耦合本构关系；Faidley等[20]对磁致伸缩作动器开展了深入的实验研究，取得了可靠的实验结果；Calkins等[21]建立了Jiles-Atherton模型和二次畴转模型组合的作动器磁滞模型；Tan等[22]提出了一种利用Preisach算子描述的磁致伸缩作动器正逆模型，并与试验进行了对比；Moon等[23]设计、制造了线性磁致伸缩作动器，研究了其动力特性，并对一个简支梁进行了振动控制试验，验证其具有良好的减振效果；Grunwald等[24]提出了磁致伸缩作动器优化设计方法。

本文针对基于磁致伸缩作动器的拉索振动控制开展研究，利用磁致伸缩作动器提供轴向控制力控制拉索横向振动，考虑拉索-磁致伸缩作动器系统的非线性特征和控制时滞，对非线性控制方法和时滞补偿算法进行了研究，并通过仿真分析验证了拉索控制效果。

1 磁致伸缩作动器模型

超磁致伸缩材料(GMM)是一种新型功能材料，其磁致伸缩系数可达到10-3量级，典型代表为TbDyFe(铽镝铁)合金。采用直径20 mm，长度120 mm的TbDyFe(铽镝铁)合金棒材，设计制造了一款磁致伸缩作动器，其内部构造及说明如图1。为了减小GMA(giant magnetostrictive actuator)迟滞现象，给磁致伸缩棒施加了3.25 MPa预压力。为了消除GMA倍频效应，在GMA中设置了偏置磁场并设置偏置电压为10 V。为了建立GMA力学模型，设计了如图2的实验装置。该实验系统采用钢丝绳连接配重施加预压力，利用了力传感器测量GMA提供控制力大小。

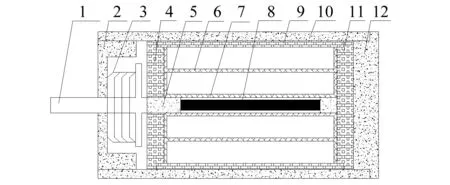
1-输出杆;2-非导磁上盖;3-预压弹簧;4-导磁上盖;5-导磁体; 6-偏置线圈骨架;7-激励线圈骨架;8-超磁致伸缩棒; 9-导磁内壁;10-非导磁外壁;11-导磁下盖;12-非导磁下盖。 其中导磁上盖和非导磁外壁上开有出线孔。图1 磁致伸缩作动器内部结构图Fig.1 The internal structure of GMA

图2 磁致伸缩作动器试验装置Fig.2 The testing apparatus of GMA

在偏置电压10 V和预压力3.25 MPa条件下，为了消除GMA的磁滞现象，在实验前要对GMA施加10 V电压进行预磁化。激励电压从-15 V开始，每次增加1 V，直至15 V，测得的GMA力与电压关系如图3(a)。进行预磁化、偏置磁场作用下，作动器施加的动态控制力情况如图3(b)所示。从图中可以看出，作动器动态情况下与静态情况下所提供的控制力相符，但存在一定范围的时滞。

根据实验数据，采用最小二乘法拟合得到磁致伸缩作动器的所提供控制力-磁关系:

U=2.232 4×V-2.134 2R2=0.99

(1)

式中:U为作动器的所提供控制力(N);V为激励电压(V);R2为回归平方和与总离差平方和的比值;R2都大于0.95;说明整体的拟合效果良好。

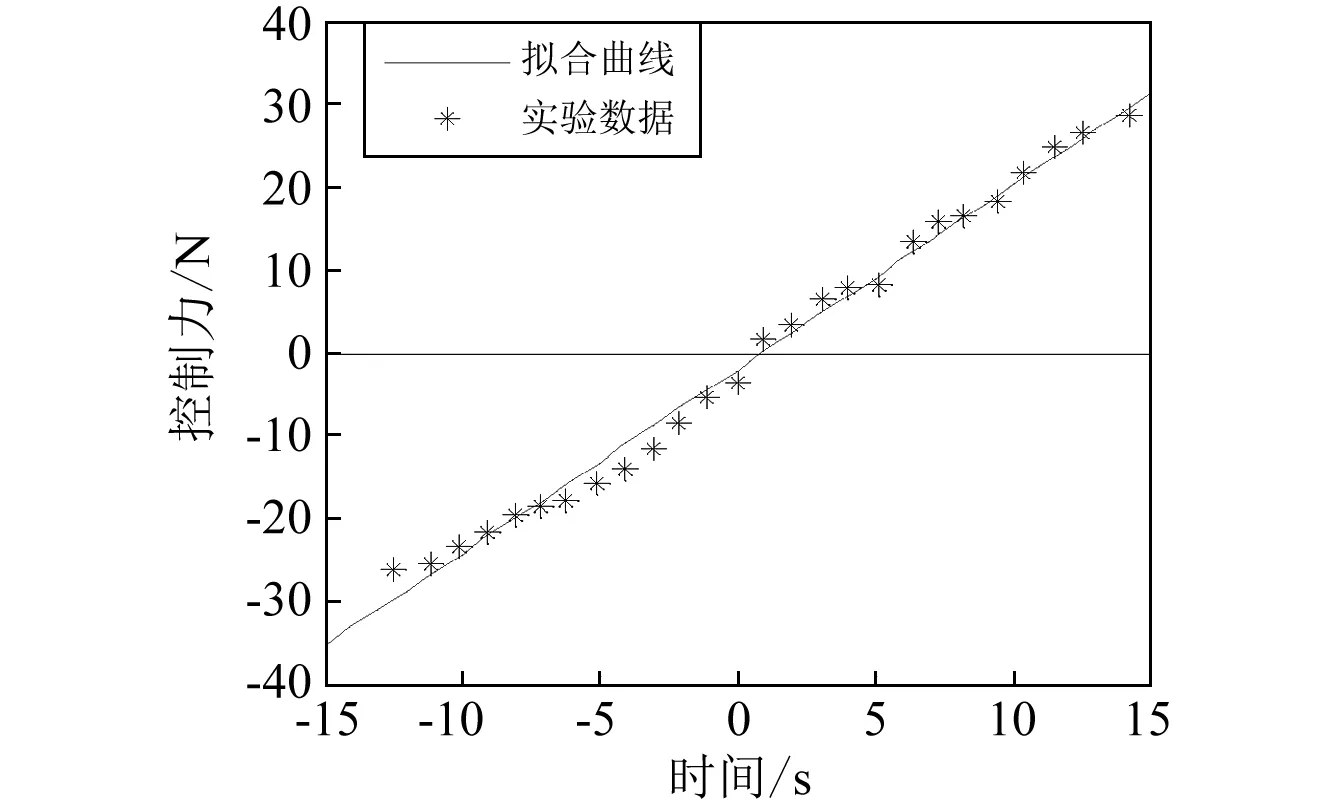
(a)静态曲线

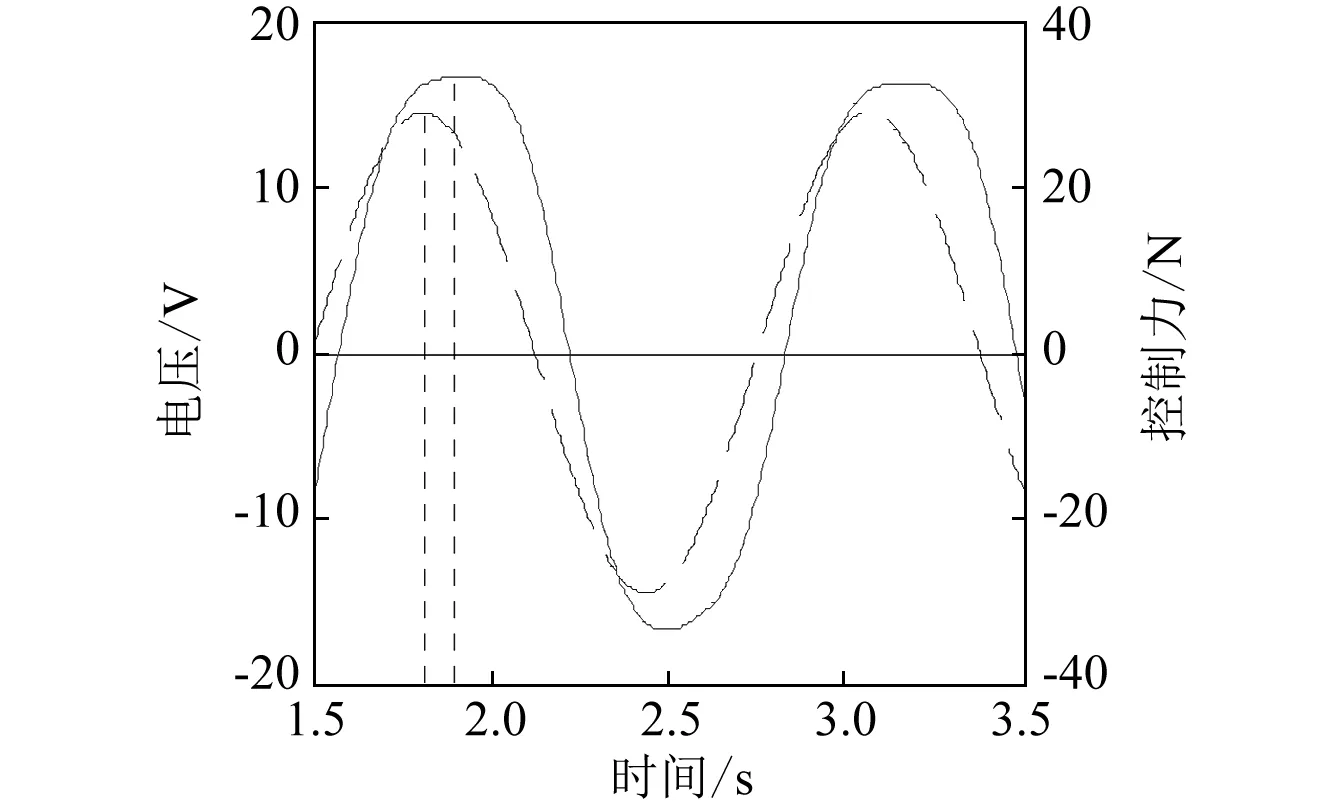
(b)动态曲线图3 控制力与激励电压的变化曲线图Fig.3 The variation graph of control force and the excitation voltage

2 考虑时滞的拉索面内轴向控制方程

采用磁致伸缩作动器施加轴向控制力，可以对拉索横向振动进行控制，拉索振动控制系统力学模型，如图4所示。设静平衡状态下初始索力为Hs，拉索沿轴向的主动控制力为U(t)，拉索单位长度质量为m，不考虑拉索抗弯刚度影响，在外部激励f(x,t)作用下的无阻尼运动方程为

图4 拉索模型与轴向主动控制力Fig.4 The stay cable model and the axial active control force

(2)

式中:v(x,t)为拉索的动位移;采用振型叠加表示为

(3)

式中:Vn(x)为第n阶振型;xn(t)为第n阶模态坐标。将式(3)代入式(2)，考虑到模态正交性可以得到n个独立的振动方程。实际工程中拉索振动通常以前几阶模态为主，考虑拉索前三阶模态和模态阻尼简化模型，可得拉索振动方程为

(4)

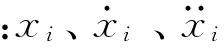
将式中(4)采用状态方程描述：

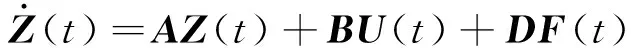
(5)

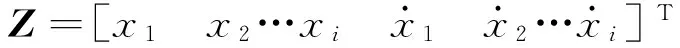
(6)

式(6)表明矩阵B为时变矩阵，因此拉索轴向振动控制系统呈现双线性特征。式(5)求解可以写成以下形式

(7)

式(7)是连续时间形式的受控方程的求解，但是实际工程运用中，信号的采集和处理都是离散时间的数据点，因而必须将连续时间系统反应响应的求解形式转换成离散时间的形式。离散化的常用手法是采用零阶保持器，例如将系统状态变量采用零阶保持器后，即变为Z(t)=Z(kΔt)，Δt为采样周期。当外激励输入、控制力输入以及振动状态变量转换为离散数据的形式后，式(5)将写成离散标准形式为

Z(k+1)=AdZ(k)+BdU(k)+DdF(k)

(8)

若控制系统存在时滞τ，则在t时刻产生的最优控制力为U(t-τ)，于是状态方程可表示为

Z(k+1)=AdZ(k)+BdU(k-nΔt)+DdF(k)

(9)

设采样周期为Δt，则在采样周期内，控制力向量U(t)，外界荷载F(t)为常量。即：

U(t)=U(kΔt)F(t)=F(kΔt)
kΔt≤t≤(k+1)Δtk=0，1，2，…

(10)

对任意时间间隔[kΔt,(k+1)Δt]状态方程式(9)的解可以写成：

(11)

3 基于移相法的时滞控制补偿方法

根据结构最优控制理论，对于多自由度系统，第i阶模态的理想控制力为

(12)

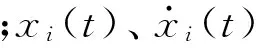
当实际控制系统存在时滞τ，第i阶模态的实际控制力为

(13)

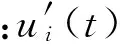
(14)

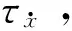
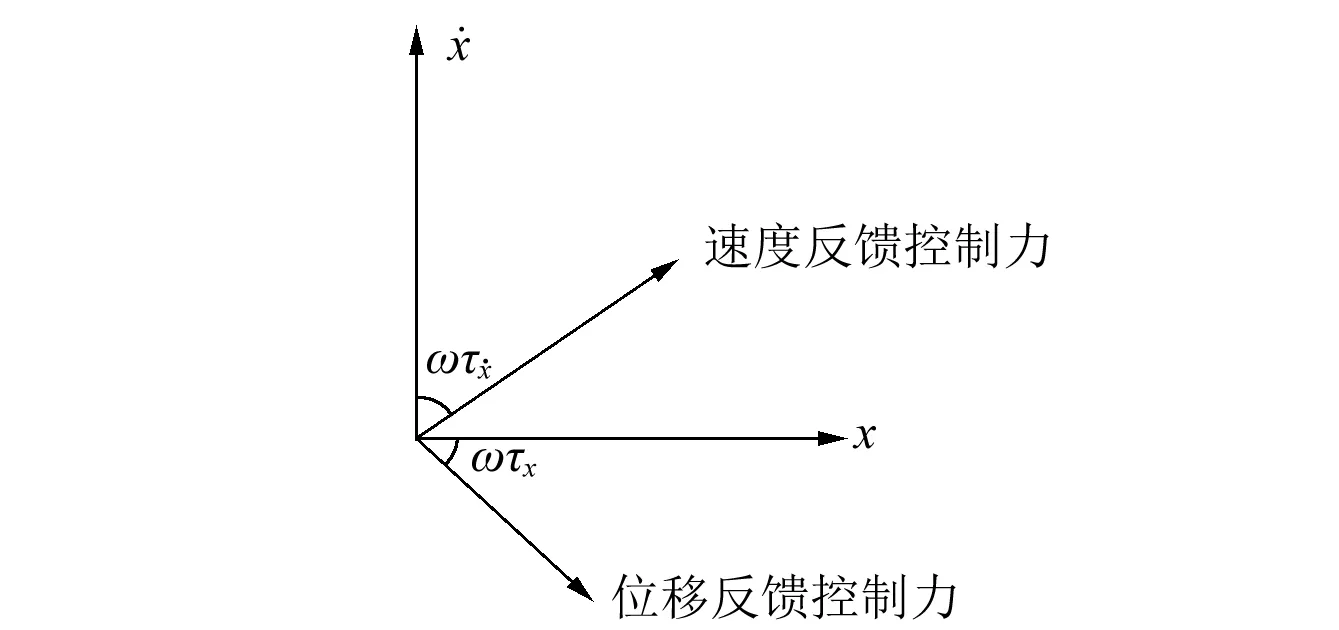
图5 反馈控制力与结构响应的相位图Fig.5 Phasor diagram of feedback forces and response for real system

(15)

式中:

对于具有n个自由度的系统，振型补偿矩阵De通过Di聚集而成，可表示为:

(16)

式中:i=1,2,…。

将振型补偿矩阵De转换为状态空间矩阵D，则可得到

(17)

式中:Ψs=[Ψ0;0Ψ];Ψ为系统的阵型矩阵。这样就可以得到时滞补偿增益矩阵G′

G′=DG

(18)

式中，G为理想状态下无时滞的状态反馈增益矩阵。

4 拉索非线性控制系统的求解方法

4.1 双线性求解方法

由式(6)可知，式(9)中矩阵Bd与状态向量相关，因此拉索-磁致伸缩作动器控制系统为双线性控制系统，采用的求解方法为逐步确定每个时刻的拉索状态量，从而逐步确定控制力，其求解流程，如图6所示。

图6 双线性计算框图Fig.6 Calculating frame of bilinear

4.2 双线性控制系统简化求解方法

采用双线性化方法求解拉索-磁致伸缩作动器控制系统需要逐步确定拉索状态向量，但在实际控制中较难实现。本文提出了二种双线性控制系统简化求解方法，其一为平均值线性化简化方法，该方法为：通过双线性法求出拉索控制系统在整个控制过程中每个时刻的状态矩阵，然后对整个控制时段的状态量求平均值，用这个值代替状态时变值，将拉索振动控制系统线性化。这样，状态矩阵B可表示为

(19)

第二种简化求解方法为初始值线性化方法，由式(6)知，状态矩阵与状态变量呈线性变化，忽略BiZ(k)项的影响，拉索非线性振动控制系统简化为线性系统，其状态矩阵简化为

(20)

4.3 线性化简化方法影响分析

为了分析上述两种线性化方法对振动控制效果的影响，定义Ψ为非线性项影响因子

(21)

式中:Bz为线性化后状态矩阵B的值，B2为矩阵B的常数项矩阵。

考虑拉索前三阶模态情况，由式(6)可知：

(22)

故矩阵B中前三项非线性影响因子为0，第五项的非线性影响因子为100%。

由拉索性质知，拉索的前三阶阻尼比ξi1，拉索振动幅值max(z(t))1，根据式(21)和式(22)知

(23)

同理知：

(24)

由式(23)和式(24)知，第四个与第六个值非线性影响因子取决于拉索本身系统以及初始索力。

5 实例仿真分析

拉索有控条件下振动控制效率定义为：

(25)

式中：XKRMS为有控条件下拉索的位移RMS值;XRMS为无控条件下拉索的位移RMS值。

5.1 拉索模型及参数

拉索模型以湖南岳阳洞庭湖大桥A10拉索为原型，按照索长缩尺20:1，建立前三阶频率基本一致的简化拉索模型并进行仿真研究[25]，具体参数见表1。

表1 模型拉索的主要参数

5.2 求解方法仿真分析

采用LQR控制算法，分别采用双线性化、平均值线性化和初始值线性化方法对拉索前三阶进行主动控制，取权重矩阵Q、R分别为

(26)

设在拉索l/8处施加RMS值1.4 N、峰值4.7 N的随机激励，采用双线性化、平均值线性化和初始值线性化控制时状态矩阵4～6项,如图7(前3项非线性影响因子为0，三种状态下的值相等)所示。双线性化求解，矩阵B中第四个值和第六个值中非线性影响因子分别为0.000 6和0.002 6，而平均值线性化情况下为0.000 3和0.001 4。四种情况下得到的拉索跨中位移分别为0.029 8 m、 0.009 1 m、0.009 3 m和0.009 5 m，减振率分别为69.46%、68.63%和68.12%，拉索跨中位移时程曲线,如图8所示。结果表明，采用平均值线性化和初始值线性化时减振率略有下降，但也取得了良好的减振效果，而两种简化方法取得的减振效果基本一致，证明简化方法是可行的。

(a)B(4) (b)B(5) (c)B(6)图7 随机激励下B矩阵变化曲线Fig.7 Change curve of matrix B under the random excitation

图8 4种控制条件下拉索跨中位移时程曲线图Fig.8 Time history of displacement at 1/2 length of cable under 4 control modes

5.3 拉索单模态时滞补偿控制仿真分析

针对拉索第一阶模态进行主动控制，采用LQR法，权重矩阵Q、R为：

(27)

在拉索l/8处施加均方根RMS值为0.5 N，峰值3.8 N的随机激励，为了能直观清晰的表达出该补偿方法的有效性，选择画出在时滞大小为0.20 s时，拉索结构在无控、理想最优控制、时滞无补偿控制和时滞补偿控制时的跨中位移时程曲线图,如图9所示。此时的跨中位移分别为0.029 8 m、0.007 4 m、0.019 9 m和0.008 1 m；减振率分别为75.22%、33.26%和72.77%。

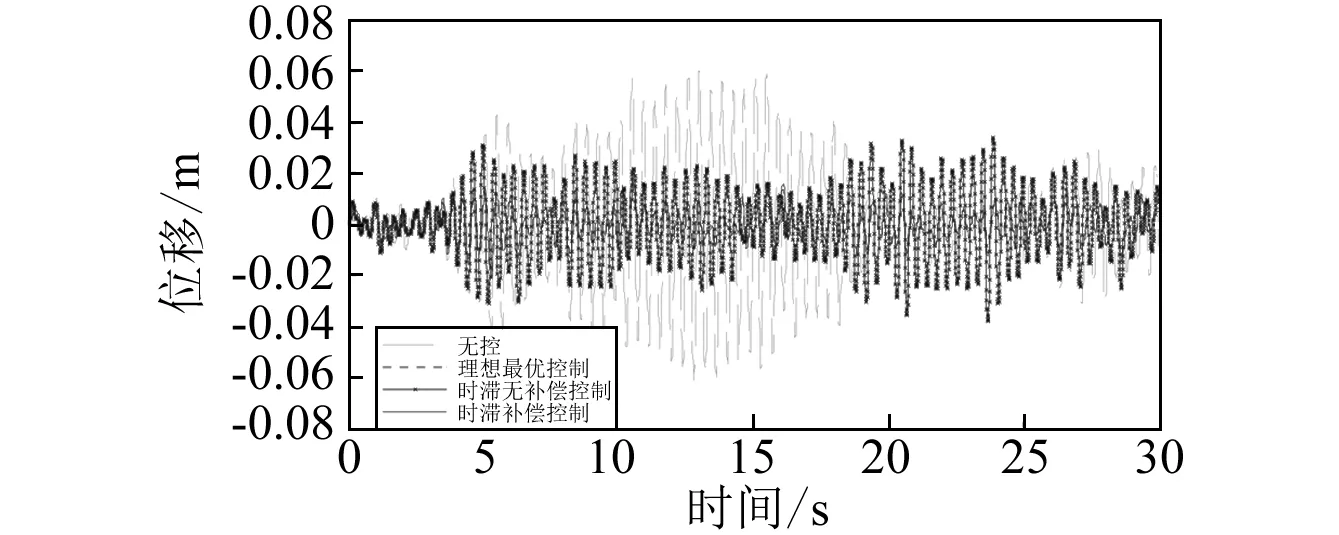
图9 时滞0.20 s时4种控制条件下拉索跨中位移时程曲线图Fig.9 Time history of displacement at 1/2 length of cable with 0.20 s time-delay under 4 control modes

不同时滞情况下的时滞补偿控制效果，如表2所示。从表2可知，随着时滞的增大，结构的控制效果在变差，进行时滞补偿后的结构的控制效果明显优于未补偿的结构的控制效果，甚至，当时滞增大到一定时，结构发散，但补偿后的结构具有一定的控制效果。

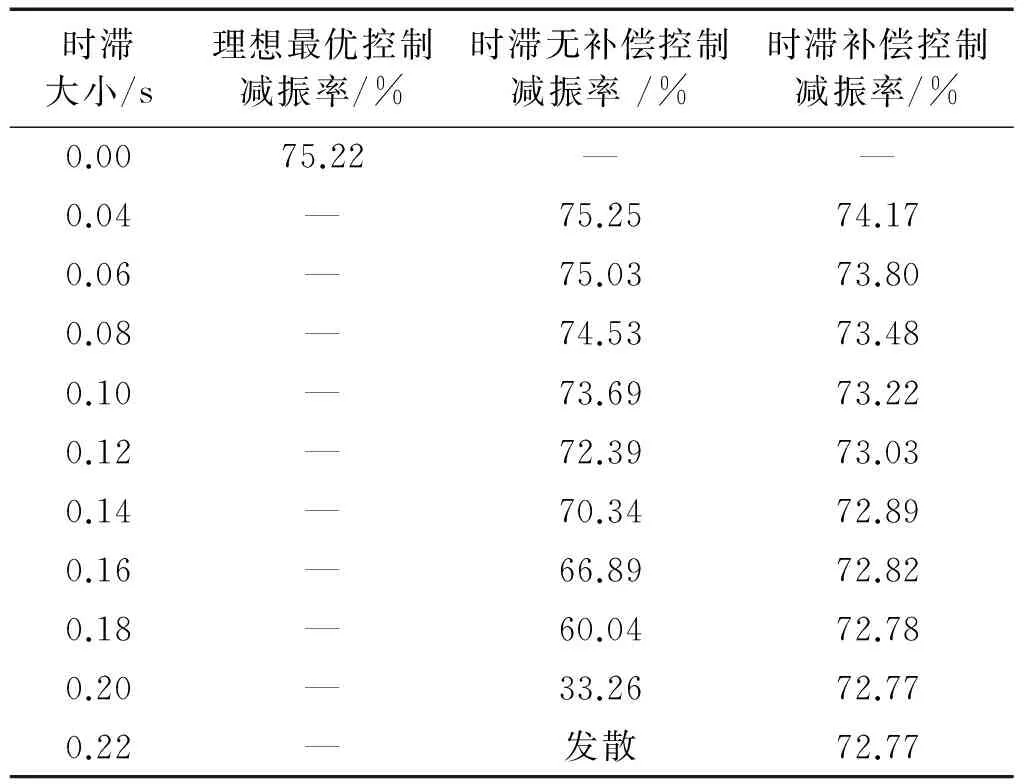
表2 单模态情况下不同时滞补偿效果

5.4 拉索多模态时滞补偿控制仿真分析

对拉索前三阶进行主动控制，采用LQR法，权重矩阵Q、R同式(27)，同样，在拉索l/8处施加与单模态情况相同随机激励，持续时间为30 s。选择时滞大小为0.10 s时，拉索结构在无控、理想最优控制、时滞无补偿控制和时滞补偿控制时跨中位移时程曲线图,如图10所示。此时的跨中位移分别为0.029 8 m、0.009 3 m、0.040 9 m和0.011 0 m；减振率分别为68.63%、-37.09%和63.22%。图11、图12分别为时滞0.10 s时拉索主动控制力时程图和磁致伸缩作动激励电压时程图。

图10 时滞0.10s时4种控制条件下拉索跨中图11 拉索主动控制力图12 激励电压时程位移时程曲线图Fig.11TheactivecontrolforceFig.12Thetime-historyofFig.10Timehistoryofdisplacementat1/2lengthofcablewith0.10stime-delayunder4controlmodesexcitationvoltage

在拉索进行前三阶模态控制情况下，不同时滞情况下的时滞补偿控制效果,如表3所示。与单模态控制情况相同的是随着时滞的增大，结构的控制效果在变差，进行时滞补偿后的结构的控制效果明显优于未补偿的结构的控制效果，不同的是考虑多模态控制更加容易发散，但移相法都能进行很好的补偿，尽管系统会随着时滞增大而发散，仍然具有较好的补偿效果。

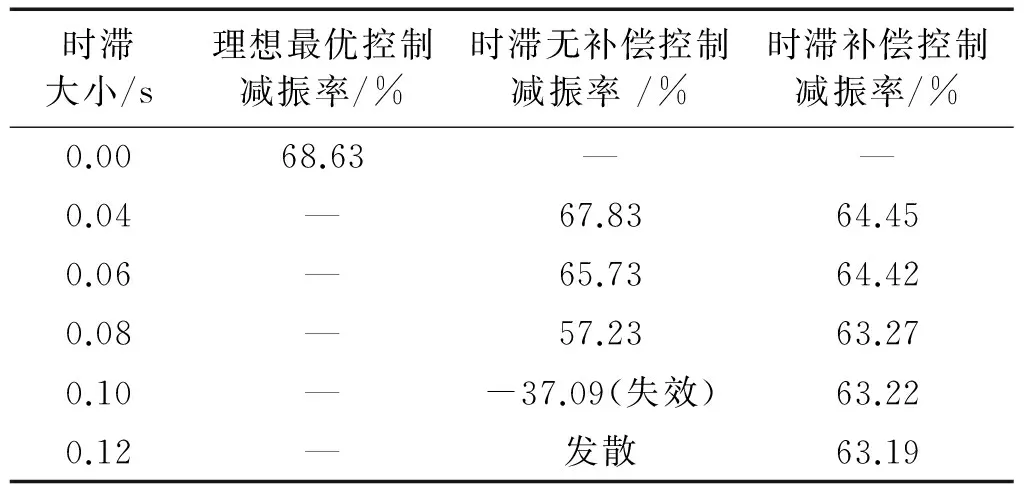
表3 多模态情况下不同时滞大小补偿效果

5.5 拉索磁致伸缩作动器减振系统实用可行性分析

仿真分析表明，采用磁致伸缩作动器进行拉索振动所需的最大控制力与拉索张力的比值<10%，减振效果>60%，如减小最大控制力，也有望达到>50%的效果，磁致伸缩作动器能提供足够的控制力，因而具有工程应用的可能，实际安装可以采用图如13所示的方式。

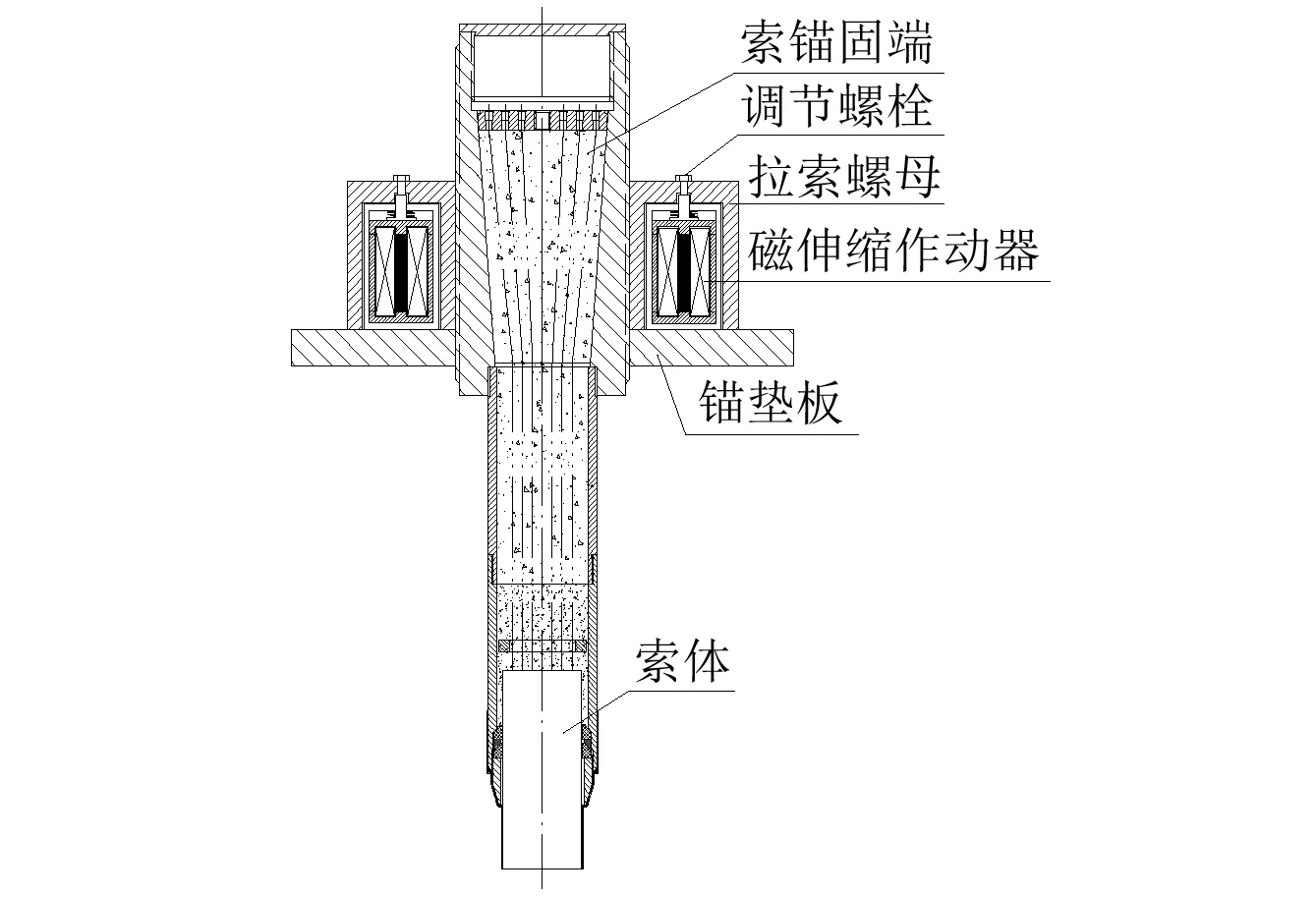
图13 磁致伸缩作动器拉索减振布置方式图Fig.13 Arrangement diagram of GMA using cable mitigation

6 结 论

本文针对拉索控制过程中产生的时滞进行时滞补偿研究，设计制造出磁致伸缩作动器，通过试验得到了磁致伸缩作动器的力-磁关系；建立了拉索面内状态方程，提出了拉索时滞补偿理论和拉索线性化方法-平均值法，通过在外部随机激励作用下开展拉索面内单、多模态控制仿真分析。得到了以下主要结论：

(1)采用超磁致伸缩材料，设计制造了磁致伸缩作动器，采用实验建立了该作动器力学模型。

(2)针对拉索-磁致伸缩作动器控制系统中的双线性振动控制问题，提出了采用B矩阵平均值线性化和初始值线性化两种简化求解方法，并对简化方法的影响进行了分析。仿真分析表明，提出的方法是可行的。

(3)考虑拉索-磁致伸缩作动器控制系统中存在的时滞，提出了移相法时滞补偿方法。仿真分析表明，针对拉索-磁致伸缩作动器系统模型，不管是单模态控制还是多模态控制，移相法都能取得良好的时滞补偿效果。当单模态时滞为0.20 s时，进行补偿后从减振率为33.26%增大到72.77%，减振率提高了39.51%；当多模态时滞为0.10 s时，系统已发散，采用移相法补偿后，减振率达到了63.22%。

[1] YAMAGUCHI H, DUNG N N．Active waves control of sagged-cable vibration[C]∥ Processing of the 1st Conference Motion and Vibration Control. Yokohama, 1992.

[2] FUJINO Y, WARNITCHAI P, PACHECO B M. Active stiffness control of cable vibration[J]. Journal of Applied Mechanics, 1993, 60(4): 948-953．

[3] SUSUMPOW T, FUJINO Y. Active control of multimodal cable vibrations by axial support motion[J]. Journal of Engineering Mechanics, 1995, 121(9):964 -972.

[4] WARNITICHAI P, FUJINO Y, SUSUMPOW T. A non-linear dynamic model for cables and its application to a cable-structure system[J]. Journal of Soundand Vibration, 1995, 187(4): 695-712.

[5] ACHKIRE Y, PREUMONT A. Active tendon control of cable-stayed bridges[J]. Earthquake Engineering and Structural Dynamics, 1996, 25: 585-597.

[6] GATTULLI V, ALAGGIO R, POTENZA F. Analytical prediction and experimental validation for longitudinal control of cable oscillations[J].International Journal of Non-Linear Mechanics, 2008, 43(1): 36-52.

[7] 周海俊，孙利民． 斜拉索风雨激振的形状记忆合金半主动控制数值模拟分析[J]. 防灾减灾工程学报，2008, 28(3): 308-312.

ZHOU Haijun, SUN Limin. Control of rain-wind-induced cable vibration by using shape memory alloy[J]. Journal of Disaster Prevention and Mitigation Engineering, 2008, 28(3): 308-312.

[8] 朱保兵，李国强. 不同边界条件下拉索振动的主动控制研究[J].力学季刊，2009，30(3):461-468.

ZHU Baobing, LI Guoqiang. Research on active vibration control of cables under different boundary conditions[J]. Chinese Quarterly of Mechanics, 2009, 30(3):461-468.

[9] 王修勇,孟庆甲,郭雪涛,等.基于磁致伸缩作动器的拉索主动控制与多级Bang-Bang控制仿真分析[J].地震工程与工程振动.2014,34(2):161-166.

WANG Xiuyong, MENG Qingjia, GUO Xuetao, et al.Research on active and multistage Bang-Bang vibration control of cables using giant magnetostrictive actuator[J].Journal of Earthquake Engineering and Engineering Vibration, 2014,34(2):161-166.

[10] YANG J N, AKBARPOUR A, ASKAR G. Effect of time delay on control of seismic-excited building [J]. Journal of Structural Engineering, 1990, 116(10): 2801-2814.

[11] 徐龙河,周云,李忠献.MRFD半主动控制系统的时滞与补偿.地震工程与工程振动,2001,21(3):127-131.

XU Longhe, ZHOU Yun, LI Zhongxian. Time-delay and compensation of MRFD semi-actiye control system[J]. Journal of Earthquake Engineering and Engineering Vibration, 2001,21(3):127-131.

[12] 王在华,胡海岩.时滞动力系统的稳定性与分岔:从理论走向应用[J].力学进展, 2013, 43(1): 3-20.

WANG Zaihua, HU Haiyan. Stability and bifurcation of delayed dynamic system: from theory to application [J]. Advances in Mechanics, 2013, 43(1): 3-20.

[13] ABDEL-ROHMAN M. Time-delay effects on active damped structures[J]. Journal of Engineering Mechanics, 1987,113( 11): 1709-1719.

[14] MCGREERY S, SOONG T T. An experiments study of time delay compensation in active structural control[C]// Proceedings of the 6th International Modal Analysis Conference. SEM, 1988.

[15] CHUNG L L, REINHORN A M, SOONG T T. Experiments on active control of seismic structures[J]. Journal of Engineering Mechanics, 1988, 114(2):241-256.

[16] 周岱, 郭军慧. 空间结构风振控制系统的神经网络时滞补偿[J]. 空间结构, 2008,14(2):8-13.

ZHOU Dai, GUO Junhui. Time delay compensation for wind-induced vibration control system of spatial latticed structure with neural network[J]. Spatial Structures, 2008,14(2):8-13.

[17] 薛晓敏，孙清，张陵，等. 基于遗传算法策略的含时滞结构振动主动控制研究[J]. 工程力学，2011，28(3)：143-149.

XUE Xiaomin, SUN Qing, ZHANG Ling,et al. Research on active control for time delayed structure using modified genetic algorithm[J]. Engineering Mechanics, 2011，28(3)：143-149.

[18] REED R S. Active vibration isolation using a magnetostrictive actuator [J].Modeling & Simulation,1988,19:73-81.

[19] CARMAN G P, MITRVIC M. Nonlinear constitutive relations for magnetostrictive materials with applications to 1D problems[J]. J Intelli Mat Syst & Stru,1995(6):673-684.

[20] FAIDLEY L E, LUND B J, FLATAU A B, et al. Tefenol-D elasto-magnetic properties under varied opening conditions using hysteresis loop analysis[C]// SPIE Symposium on Smart Structures,1998.

[21] CALKINS F T, SMITH R C, FLARAU A B. Energy-based hysteresis model for magnetostrictive transducers[J]. IEEE Trans Magn,2000,36(2):429-439.

[22] TAN X, BARAS J S. Modeling and control of hysteresis in magnetostrictive actuators[J]. Automatica, 2004, 40 (9): 1469-1480.

[23] MOON S J, LIM C W, KIM B H, et,al. Structural vibration control using linear magnetostrictive actuators[J]. Journal of Sound and Vibration, 2007, 302(4/5):875-891.

[24] GRUNWALD A, OLABI A G. Design of a magnetostrictive (MS) actuator[J]. Sensors and Actuators A, 2008, 144 (1): 161-175.

[25] 王修勇．斜拉桥拉索振动控制新技术研究[D]．长沙：中南大学，2002.

Time delay compensation for the active cable vibration control using giant magnetostrictive actuators

SUN Hongxin, LI Jianqiang, WANG Xiuyong, FANG Cong

(School of Civil Engineering, Hunan University of Science and Technology, Xiangtan 411201, China)

The large amplitude vibration of stay cables will give rise to the safe operation risk on the cable-stayed bridges. It is a kind of feasible method for the cable vibration control using the axial force provided by a giant magnetostrictive actuator(GMA). However, time delays, frequently encountered in the actual control system, can diminish the performance and stability of the stay cable vibration control system. The dynamic model of the GMA and motion equation of the stay cable coupling GMA control system were established. Focusing on the cable coupling GMA control system with time delay and nonlinearity, the time delay compensation theory was presented based on the phase shift method, and the linearization method for the control system was put forward. The delay compensation effect on the cable coupling GMA control system was revealed by simulation analysis. The results show that the phase shift method can achieve good effect of time-delay compensation in the above system, which is close to the vibration reduction rate of an optimal control without delay.

stay cable; giant magnetostrictive actuator; time delay compensation; phase shift method; simulation analysis

国家重点基础研究发展计划(973计划)项目(2015CB057702);国家自然科学基金项目(51378203)

2016-01-25 修改稿收到日期： 2016-06-01

孙洪鑫 男，博士，副教授，1980年生

王修勇 男，教授，博士生导师，1962年生

U448.27

A

10.13465/j.cnki.jvs.2017.14.033