旋转叶片-机匣碰摩振动响应分析

马 辉, 孙 祺, 太兴宇, 郝玉明， 闻邦椿

(1. 东北大学 机械工程与自动化学院，沈阳 110819；2. 机械结构强度与振动国家重点实验室，西安 710049； (3. 沈阳鼓风机集团股份有限公司,沈阳 110869)

旋转叶片-机匣碰摩振动响应分析

马 辉1,2, 孙 祺1, 太兴宇3, 郝玉明3， 闻邦椿1

(1. 东北大学 机械工程与自动化学院，沈阳 110819；2. 机械结构强度与振动国家重点实验室，西安 710049； (3. 沈阳鼓风机集团股份有限公司,沈阳 110869)

以航空发动机压气机叶片为研究对象，基于ANSYS有限元软件，考虑离心刚化、旋转软化以及科氏力对叶片的影响，采用变厚度壳单元建立了旋转叶片的有限元模型。假定圆盘与机匣存在静态不对中，叶片由于离心力的作用产生径向伸长，从而使叶尖与机匣内壁发生碰摩。根据叶尖处每个节点径向位移与间隙之间的位置关系，对不同转速下叶片-机匣碰摩过程进行数值仿真。研究结果表明：对于扭形叶片，叶尖只有部分节点与机匣发生碰摩；碰摩结束后，叶片振动响应以低阶动频形式进行衰减，连续的周期碰摩产生的倍频成分在与之接近的动频处会出现幅值放大现象。研究结果可为叶片结构设计及叶片-机匣碰摩故障诊断提供理论依据。

变厚度壳单元；叶片-机匣碰摩；高频振动；动频；幅值放大

为提高发动机的性能和效率，就要使转子叶尖与机匣的间隙尽可能小，以减少因工作介质泄漏而造成的损失。然而间隙过小，会导致高速旋转的叶片在离心载荷的作用下与机匣发生碰撞。由于叶尖处有着较大的线速度，碰撞能量大，所以碰摩一旦发生，就会造成严重的后果。据美国运输部报道：在1962—1976年间的417百万飞行小时中，10.2%的发动机转子事故是由于转静子之间碰摩引起的[1]。

Padovan等[2]将叶片简化为悬臂梁，推导了法向接触力和叶片径向变形之间的关系，分析了在单叶片和多叶片碰摩情况下，不平衡量、叶片/转子刚度、系统阻尼和摩擦对系统非线性动力学特性的影响。Sinha[3]研究了带叶片的柔性转子与刚性机匣的碰撞动力学特性，碰摩通过附加的刚度矩阵和阻尼矩阵来模拟，研究发现当叶尖与机匣发生接触时，接触力类似于Hertzian接触产生的力。Lesaffre等[4-5]基于Sinha提出的转子叶片模型，并将叶片进一步简化成具有两自由度的集中质量块模型，机匣简化成柔性环，研究了叶片转子转速大于临界转速时引起机匣-叶片系统的不稳定现象。太兴宇等[6]建立旋转叶片的连续体解析模型，采用间隙函数判定，确定碰摩是否发生，分析了科氏力对碰摩响应的耦合作用。

根据试验测试叶片-机匣接触力结果，发现对于叶片单点以及局部碰摩，其接触力类似于周期性脉冲力[7-9]，根据这一特定碰摩情况，一些学者提出了基于脉冲力模型的碰摩故障模拟。Sinha[10]提出基于旋转的Timoshenko悬臂梁模型理论，应用数值方法分析了不同的摩擦参数和接触时间对于叶片频率的影响以及叶片的非线性动力学响应特性。Turner等[11-12]将碰摩力简化为脉冲力，分析了叶片机匣连续撞击情况下的瞬态动力学特性，确定了叶尖接触力分布和叶片在不同碰摩情况下的振动形式。太兴宇等[13]采用Timoshenko梁单元建立了旋转叶片在脉冲力作用下的动力学方程，并分析了不同激振频率下叶片的振动响应。

为了更加精确地描述叶片-机匣之间的碰摩特征，一些学者采用接触动力学理论来模拟叶尖与机匣的接触特性。Legrand等[14]采用数值计算以及软件分析辅助的方法研究了内侧带有阻尼涂层的机匣与叶尖接触的特性。Roques等[15]以某核电厂汽轮发电机组的转子系统为研究对象，建立了相应的转子-静子有限元模型，基于接触动力学理论分析了转轴与静子隔板间的碰摩现象。刘书国等[16]对航空发动机叶片-机匣碰摩过程进行了数值模拟，考虑实际叶片的叶形特征，分析叶片顶部受瞬时碰撞与摩擦载荷(碰摩载荷)作用下的动力学影响特征。

通过对上述文献的分析发现，解析模型通常采用较为简单的悬臂梁和悬臂板模型，并且大多采用脉冲加载的方式来模拟碰摩过程，并不能真实的反映实际的碰摩情况；而基于接触动力学的方法，可以较为真实的模拟碰摩过程，但是需要耗费大量的计算时间，效率较低。考虑离心刚化、旋转软化和科氏力的影响，本文采用变厚度壳单元对真实叶片进行有限元建模，建立笛卡尔坐标系下的间隙函数，对叶尖各个节点进行间隙判定，确定碰摩发生的位置，并讨论了不同转速下叶片的碰摩响应。

1 旋转叶片振动的有限元动力学方程

旋转叶片振动的动力学方程可表示为

(1)

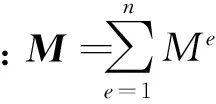
令C1=C+G,K1=K+S-Kspin，旋转叶片的动力学方程可转化为

(2)

2 叶片-机匣碰摩动力学仿真

2.1 变厚度壳叶片的有限元模型

由于真实叶片为变截面扭形叶片，本文基于ANSYS有限元软件，通过抽取叶片中面数据，根据叶片型线数据，将叶片的厚度ε拟合为随空间位置变化的变量，进而将叶片简化为变厚度壳单元。本文采用Shell181单元来模拟变厚度扭形叶片，此单元具有四个节点，每个节点有六个自由度，分别是沿X、Y、Z方向的平动自由度和绕X、Y、Z轴的转动自由度。叶尖沿宽度方向等分成20份，21个位置。图1为变厚度壳叶片有限元模型，给出了叶尖每个位置的节点号。变厚度壳叶片的有限元模型适合分析薄及中等厚度的板壳结构零件，并支持线性、大扭转和大应变，变厚度非线性等分析。将ε拟合为如下表达式[17]

ε=a0+a1x+a2y+a3z+a4xy+a5xz+a6yz+a7x2+a8y2+a9z2+a10x2y+a11x2z+a12y2x+a13y2z+a14z2y+a15z2x+a16x3+a17y3+a18z3

(3)

2.2 叶片的固有特性

叶片动频是指叶片绕盘轴旋转时的自振频率，它随转速的变化而变化，即是转速的函数。图2为叶片前5阶动频随转速的变化曲线。由图可知随着转速的增加各阶动频随之增大。

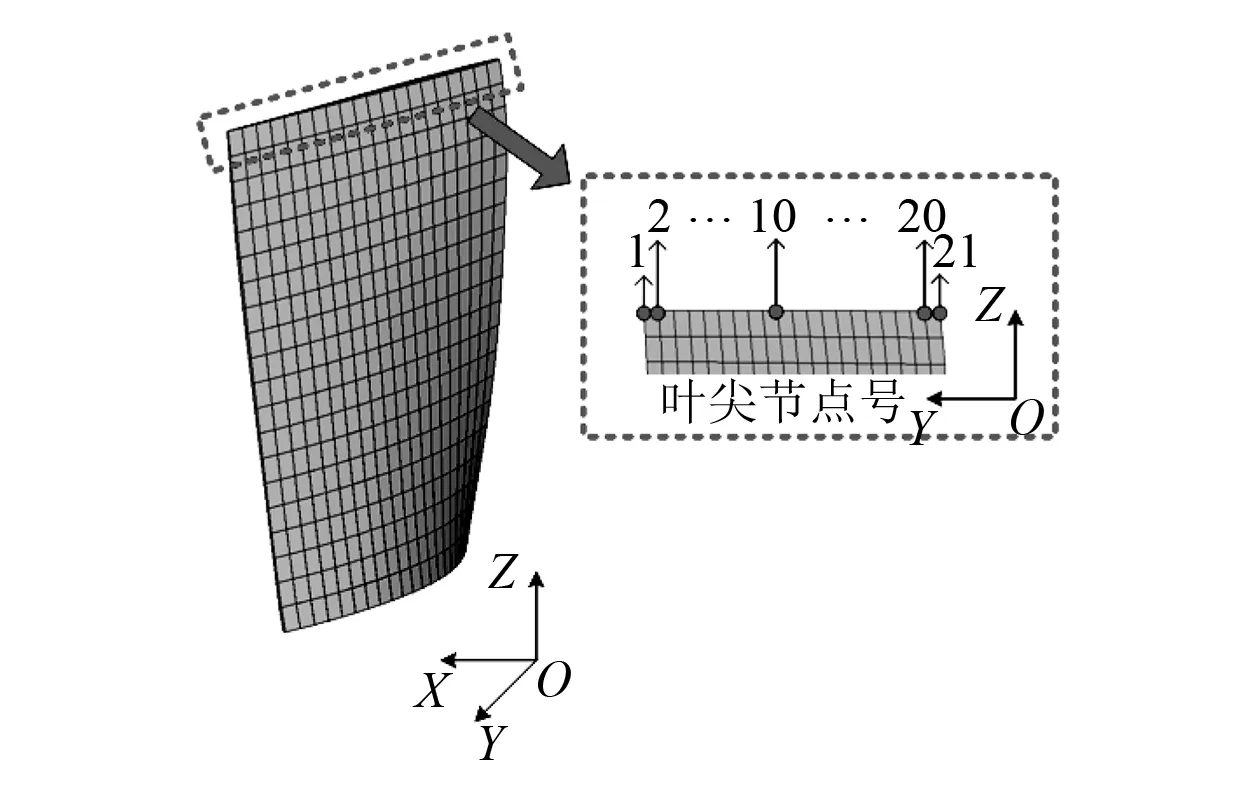
图1 变厚度壳叶片有限元模型Fig. 1 Finite element model of blade

选用的叶片参数如下：叶片弹性模量E=1.25×1011Pa，密度ρ=4 370 kg/m3，泊松比υ=0.3，圆盘半径Rd=216.52 mm。忽略叶根-圆盘榫连结构的影响，这里叶根的约束形式为完全固支。

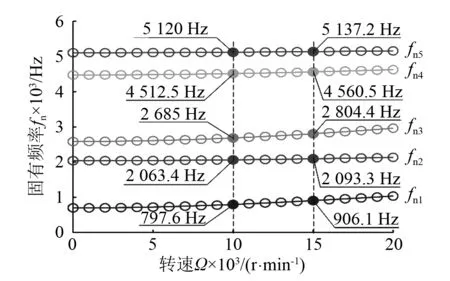
图2 叶片动频Fig. 2 Dynamic frequencies of the blade

2.3 间隙函数

假设机匣与圆盘存在静态平行不对中，并且叶片具有安装角，则叶尖与机匣内壁之间的间隙呈不均匀分布。图3为不对中叶片-机匣间隙示意图。图3(b)中O和O1分别为圆盘中心和机匣中心；L为叶片长度；Rc为机匣半径；rg为叶尖轨迹半径，rg=L+Rd;Rd为圆盘半径。

图3 叶片-机匣间隙示意图Fig. 3 Schematic diagram of the clearance between blade and casing

ANSYS在模拟叶片-机匣的碰摩过程中，在叶片上施加的是转速效应，叶片并不转动，因此在笛卡尔坐标系下，通过建立时变的间隙函数来模拟叶尖径向和机匣之间的间隙。由于叶片存在安装角，叶尖各节点在XOZ平面上的投影的位置不同，导致在叶尖各节点处存在不同的初始相位φi，从而出现不同的初始间隙ci。在图3(b)中lO1B=Rc,lOiO=Rc-cmin-rg,lOA=rg,lAB=ci,∠O1OA=π-Ωt,根据正弦定理建立笛卡尔坐标系下的叶片-机匣的初始间隙函数如下

ci=Rcsin(π/2-θi(t))/sin (π/2+φi(t))-rg

(4)

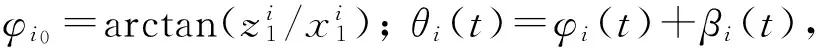
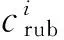
(5)

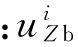
为了更加真实的反映碰摩力在叶尖上的分布情况，叶尖处的每个节点都要判定是否侵入，从而确定是否发生碰摩。叶尖节点i的侵入量δi的表达式如下

(6)

叶尖各个节点的碰摩力值需要根据对应节点位置的侵入量来分配，其表达式为

(7)

(8)

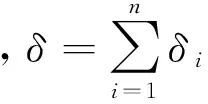
fn表达式如下

(9)

式中：Γ1=Γ0/kc,

Γ0=3EI/L3+ρAΩ2(81L/280+3Rd/8),

α=(Rd+L)/L

其中L为叶片长度；EI为叶片抗弯刚度；A为叶片横截面积；Ω为转速。由于航空发动机机匣的厚度一般为1～2 mm，所以这里设机匣的当量刚度kc=5×106N/m，摩擦因数μ=0.3。根据以上分析，得出模拟碰摩过程的流程图，如图4所示。

图4 叶片-机匣碰摩模拟过程流程图Fig. 4 Flowchart of blade-casing rubbing simulation process

2.4 稳态响应分析

在碰摩模拟过程中，先使叶片在离心力作用下运动，叶片振动响应稳定后，再施加碰摩载荷。本文对叶片在5 000 r/min，10 000 r/min和15 000 r/min三种转速下的稳态响应进行分析。

图5为不同转速下叶片节点1、节点13和节点

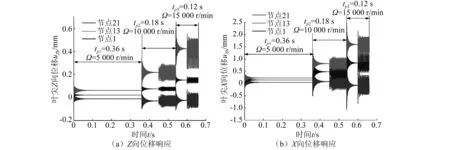
图5 不同转速下叶尖碰摩位移响应Fig. 5 Tangential rubbing-induced displacement responses under different rotational speeds

21的碰摩位移响应。从图中可以看到，转速为5 000 r/min时，叶尖各个节点的Z向位移均没有超过最小间隙值，此时只有叶片在离心力作用下产生的位移；当转速达到10 000 r/min时，节点21的Z向位移超过了最小间隙，于是在节点21处发生碰摩，而节点1和节点13的Z向位移都没有超过最小间隙值，但是依然在碰摩时产生相应的位移。表明扭形叶片在节点21处发生碰摩时，会连带叶尖其他节点处产生位移。而当转速达到15 000 r/min时，节点13的Z向位移也超过了最小间隙，故节点13处除了有碰摩位移也会出现其他节点的连带位移。图中，节点1处实际上并没有发生碰摩，并且Z向位移随着转速的增加而减小，说明扭形叶片自身的形状对节点1是否发生碰摩有很大的影响。

由图5可知，在5 000 r/min时叶尖各节点都不与机匣发生碰摩，所以下面只给出10 000 r/min和15 000 r/min下不同时刻各节点的Z向碰摩力，如图6所示。从图中可以更加清楚的分析叶尖各节点处发生碰摩的情况。在图6(a)中，叶尖处只有沿Y轴负方向的5个节点处(节点17、18、19、20和21)发生碰摩，碰摩接触时间越长，碰摩力越大。而图6(b)中发生碰摩的节点数要多于图6(a)，同样为沿叶片Y轴负方向的部分节点发生碰摩。结果表明，变厚度扭形叶片在离心力作用下，叶尖与机匣会发生局部碰摩。

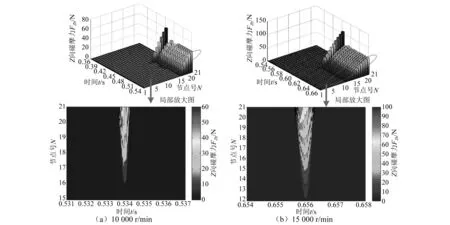
图6 不同转速下不同时刻各节点的Z向碰摩力Fig. 6 Forces of each node at different moments in Z direction under different rotational speeds

由图6可知，节点21处的碰摩最严重，因此这里分析节点21处位移响应特征。图7为10 000 r/min和15 000 r/min转速时节点21处的X向位移响应。单周期碰摩响应指仅碰摩1次后的自由振动响应，其频谱图的峰值对应的频率为叶片的动频。由图7可得以下特征：单周期碰摩时节点21的X向位移幅值随着时间逐渐衰减；在多周期碰摩发生之后，叶尖节点21逐渐稳定为周期运动；10 000 r/min下叶片碰摩的振动形式主要由1阶振型(1阶弯曲)、2阶振型(1阶扭转)、3阶振型(2阶弯曲)组成，位移响应的频率特征表现为在1阶动频处 (5×)、2阶动频处 (12×)和3阶动频处 (16×)出现幅值放大现象；15 000 r/min下碰摩发生时叶尖的振动形式主要由1阶振型(1阶弯曲)、2阶振型(1阶扭转)、3阶振型(2阶弯曲)和4阶振型(弯曲与扭转耦合)组成，其频率特征为在1阶动频处 (3×)、2阶动频处 (8×) 、3阶动频处 (11×)和4阶动频处(17×)出现幅值放大现象；10 000 r/min和15 000 r/min的单周期碰摩响应频谱图的峰值所对应的叶片动频与ANSYS中求出的叶片动频比较吻合。

3 结 论

考虑了叶片的旋转效应的影响，采用变厚度壳单元建立了叶片的有限元模型，建立了笛卡尔坐标系下的间隙函数，对叶尖各个节点进行间隙判定，从而确定碰摩发生的位置。通过对不同转速下的稳态碰摩响应分析，得到以下结论：

(1) 对于真实的叶片，由于其复杂的曲面特征，叶尖上一侧点的径向位移随着转速的增加而增加，另一侧由于弯扭运动，径向位移减小。当叶尖一侧节点的径向位移超过最小间隙时，只会在部分节点处发生局部碰摩，另一侧节点处则产生连带运动。

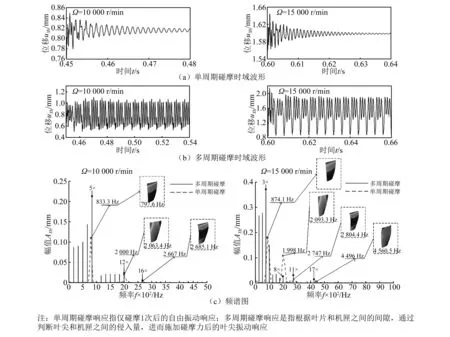
图7 10 000 r/min和15 000 r/min时节点21的X向位移响应Fig. 7 Displacement response of node 21 in X direction at 10 000 r/min and 15 000 r/min

(2) 叶片在碰摩载荷的作用下叶片振动在叶片弯曲、扭转和弯扭耦合动频处会出现较大的幅值，而叶片的弯曲振动更容易被激发。并且在高转速情况下叶片的振动形式会更为复杂，更容易激发更高阶的动频响应。

[1] IKEDA T, ISHIDA Y, YAMAMOTO T, et al. Nonlinear forced oscillations of an unsymmetrical shaft and an unsymmetrical rotor with quartic nonlinearity [J]. Bulletin of the JSME, 1988, 31(3): 530-538.

[2] PADOVAN J, CHOY F K. Nonlinear dynamics of rotor/blade/casing rub interactions[J]. Journal of Turbomachinery, 1987, 109: 527-534.

[3] SINHA S K. Dynamic characteristics of a flexible bladed-rotor with Coulomb damping due to tip-rub[J]. Journal of Sound and Vibration, 2004, 273: 875-919.

[4] LESAFFRE N, SINOU J J, THOUVEREZ F. Contact analysis of a flexible bladed-rotor[J]. European Journal of Mechanics A/Solids, 2007, 26: 541-557.

[5] LESAFFRE N, SINOU J J, THOUVEREZ F. Stability analysis of rotating beams rubbing on an elastic circular structure[J]. Journal of Sound and Vibration, 2007, 299(1): 1005-1032.

[6] 太兴宇, 马辉, 谭祯, 等. 基于连续体旋转梁模型的碰摩故障动力学特征分析[J]. 振动与冲击, 2013, 32(18): 43-48. TAI Xingyu, MA Hui, TAN Zhen, et al. Dynamic characteristics of a continuous rotating beam model with a rubbing fault[J]. Journal of Vibration and Shock, 2013, 32(18): 43-48.

[7] CHEN G. Study on the recognition of aero-engine blade-casing rubbing fault based on the casing vibration acceleration [J]. Measurement, 2015, 65: 71-80.

[8] CHEN G. Simulation of casing vibration resulting from blade-casing rubbing and its verifications [J]. Journal of Sound and Vibration, 2016, 361: 190-209.

[9] MA H, TAI X, HAN Q, et al. A revised model for rubbing between rotating blade and elastic casing [J]. Journal of Sound and Vibration, 2015, 337: 301-320.

[10] SINHA S K. Non-linear dynamic response of a rotating radial Timoshenko beam with periodic pulse loading at the free-end[J]. International Journal of Nonlinear Mechanics, 2005, 40: 113-149.

[11] TURNER K, ADAMS M, DUNN M. Simulation of engine blade tip-rub induced vibration[C]∥Proceedings of GT2005, Ren-Tahoe. Nevada, USA, 2005.

[12] TURNER K, DUNN M, PADOVA C. Airfoil deflection characteristics during rub events[J]. Journal of Turbomachinery, 2012, 134: 011018-1-7.

[13] 太兴宇, 马辉, 谭祯, 等. 脉冲力加载下的叶片-机匣动力学特性研究[J]. 东北大学学报(自然科学版), 2012, 33(12): 1759-1799. TAI Xingyu, MA Hui, TAN Zhen, et al. Research on dynamic characteristics of blade-casing with impulse loading [J]. Journal of Northeastern University (Natural Science), 2012, 33(12): 1759-1799.

[14] LEGRAND M, BATAILLY A, PIERRE C. Numerical investigation of abradable coating removal in aircraft engines through plastic constitutive law[J]. Journal of Computational and Nonlinear Dynamics, 2012, 7: 011010-1-11.

[15] ROQUES S, LEGRAND M, CARTRAUD P, et al. Modeling of a rotor speed transient response with radial rubbing [J]. Journal of Sound and Vibration, 2010, 329: 527-546.

[16] 刘书国，洪杰，陈萌. 航空发动机叶片-机匣碰摩过程的数值模拟[J]. 航空动力学报, 2011, 26(6): 1282-1288. LIU Shuguo, HONG Jie, CHEN Meng, et al. Numerical simulation of the dynamic process of aero-engine blade-to-case rub-impact [J]. Journal of Aerospace Power, 2011, 26(6): 1282-1288.

[17] 马辉，太兴宇，张志，等. 根部联接刚度对旋转叶片振动特性的影响[J]. 东北大学学报(自然科学版)，2013, 34(2): 265-270. MA Hui, TAI Xingyu, ZHANG Zhi, et al. Influence of root connecting stiffness on vibration responses of rotating blades [J]. Journal of Northeastern University (Natural Science), 2013, 34(2): 265-270.

Vibration response analysis on the rotating blade-casing rubbing

MA Hui1,2，SUN Qi1，TAI Xingyu3，HAO Yuming3，WEN Bangchun1

(1.School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819,China; 2.State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China;3.Shengu Group Compressor Co., Ltd., Shenyang 110869, China)

Taking a compressor blade as the research object and considering the influences of centrifugal stiffening, spin softening and Coriolis force, a finite element model of the rotating blade was established by using the variable thickness shell element based on ANSYS software. Assuming that there is a static misalignment between the disk and casing, the blade will generate a radial elongation under the impact of centrifugal force, moreover, the blade-casing rubbing will appear. The numerical simulation on rubbing processes under different rotational speeds was carried out according to the location relation between the radial displacements and the clearances at each top node of the blade. The results show that the rubbing only occurs on partial nodes for twisting blades, the vibration response of the blade will present a decay with a low-order dynamic frequency, the amplitude amplification phenomenon will appear when the continual periodic rubbing caused multiple frequency components are close to corresponding dynamic frequencies during rubbing. The simulation results provide a theoretical foundation to the blade structure design and the fault diagnosis on blade-casing rubbing.

variable thickness shell element; blade-casing rubbing; high-frequency vibration; dynamic frequency; amplitude amplification

国家自然科学基金委员会与中国民用航空局联合资助项目(U1433109)；中央高校基本科研业务费专项资金(N140301001； N150305001)

2016-01-19 修改稿收到日期： 2016-06-17

马辉 男，博士，教授，1978年生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.14.004