两激振器同一旋转轴线振动系统的自同步理论

陈晓哲， 窦景欣， 孔祥希， 闻邦椿

(1.东北大学 机械工程与自动化学院，沈阳 110819; 2. 东北大学 控制工程学院，秦皇岛 066004)

两激振器同一旋转轴线振动系统的自同步理论

陈晓哲1,2， 窦景欣1， 孔祥希1， 闻邦椿1

(1.东北大学 机械工程与自动化学院，沈阳 110819; 2. 东北大学 控制工程学院，秦皇岛 066004)

对两激振器同一旋转轴线振动系统的自同步理论进行了研究。采用拉格朗日方程建立振动系统的运动微分方程。应用小参数平均法获得两激振器的无量纲耦合方程，进而将该类振动系统的同步问题简化为小参数无量纲耦合方程零解的存在性与稳定性问题。由无量纲耦合方程零解存在的条件得出了两激振器实现同步运动的同步性条件，并根据Routh-Hurwitz判据得到了两激振器同步运动的稳定性条件。分析振动系统选择运动特性可知，在远共振的情况下当激振器的旋转中心距离质心的距离大于机体的当量回转半径时，振动系统实现相位差为0°的空间圆周运动；反之，振动系统实现相位差为180°的空间圆锥运动。最后通过试验验证了理论分析的正确性。

自同步；同步性；稳定性；相位差

振动磨机是一种高效、节能的新型粉磨设备，主要解决冶金、化工、非金属矿、医药、陶瓷、建筑新材料、水泥、磁性材料等诸多行业超细粉体加工难题。为满足日益增长的超细粉加工的需要，振动磨机正在向大型化方向发展。 对于大型振动磨机，由于筒体长度较大，已经不适合用一台电机驱动两个激振器，而设计制造这种多电机驱动的大型振动磨机，还有很多理论上的问题需要解决。应用自同步理论，采用两台电机分别驱动两个激振器，使振动磨机的两个激振器在较大距离下安装，这样保证其结构简单合理，降低了其制造成本，提高其工作效率。

Huygnens于1665年最早发现机械系统的自同步现象。他发现并排悬挂在同一木梁上的两个钟摆能够实现同步运动。自此之后，学者们在机械系统的自同步理论上做了大量的理论探索与试验研究，取得了丰富的成果。Blekhman[1]首次实现了机械系统的同步运动，并提出了两激振器振动机械的自同步理论。闻邦椿等[2]应用平均法求得了两激振器自同步振动机械的同步性条件和稳定性条件。在此基础上，Zhao等[3-4]将小参数摄动法引入平均法提出小参数平均法，将同步问题转化为零值解的存在性和稳定性的问题。振动系统的同步过程是电机与电机、电机与振动体之间的机电耦合过程。Dimentberg等[5]采用数值方法研究了两机驱动振动系统的瞬态同步问题。Palacios等[6]将两台直流电机带动的偏心转子安装在非线性梁上来研究非线性系统的同步运动问题。与Palacios的悬臂梁模型不同，Balthazar等[7]将两台直流电机安装在门式钢架上来研究同步运动问题。Danuta等[8]对具有非线性阻尼和刚度的两台直流电机带动偏心转子驱动振动系统的倍频和次频同步进行了研究。

前面所述的大量成果，它们都是以两个或多个激振器轴线在同一平面上的振动系统为研究对象，但是对于空间两个激振器同一旋转轴线的振动系统的同步问题，还没有得到很好地解决，这已成为该类机械发展的瓶颈。杨万东等[9]以同一轴线上两激振器驱动的振动磨为研究对象，讨论机体的运动轨迹随相位差的变化规律。Miklos等[10-12]提出两激振器的旋转轴重合布置方案用于手持类设备，应用振动系统选择运动特性来改变振幅。

综上所述，研究两激振器同一轴线振动系统的自同步理论具有重要的理论价值和实际意义。

本文以两激振器同一旋转轴线且同向旋转驱动的振动系统为研究对象，通过拉格朗日方程建立其动力学模型，得到振动系统的运动微分方程及稳态响应，并在此基础上应用小参数平均法得到了该类振动系统的同步性条件和同步运动的稳定性条件，最后通过试验来验证理论分析的正确性。

1 系统动力学模型

如图1所示，为两激振器同一旋转轴线振动系统的空间动力学模型，其由振动体m以及两个激振器m1和m2组成。两个激振器m1和m2对称地安装在振动体m左右两侧，分别由两台电机驱动并做同向旋转运动。振动体m通过弹簧支撑，同时弹簧对称地安装在固定架上。

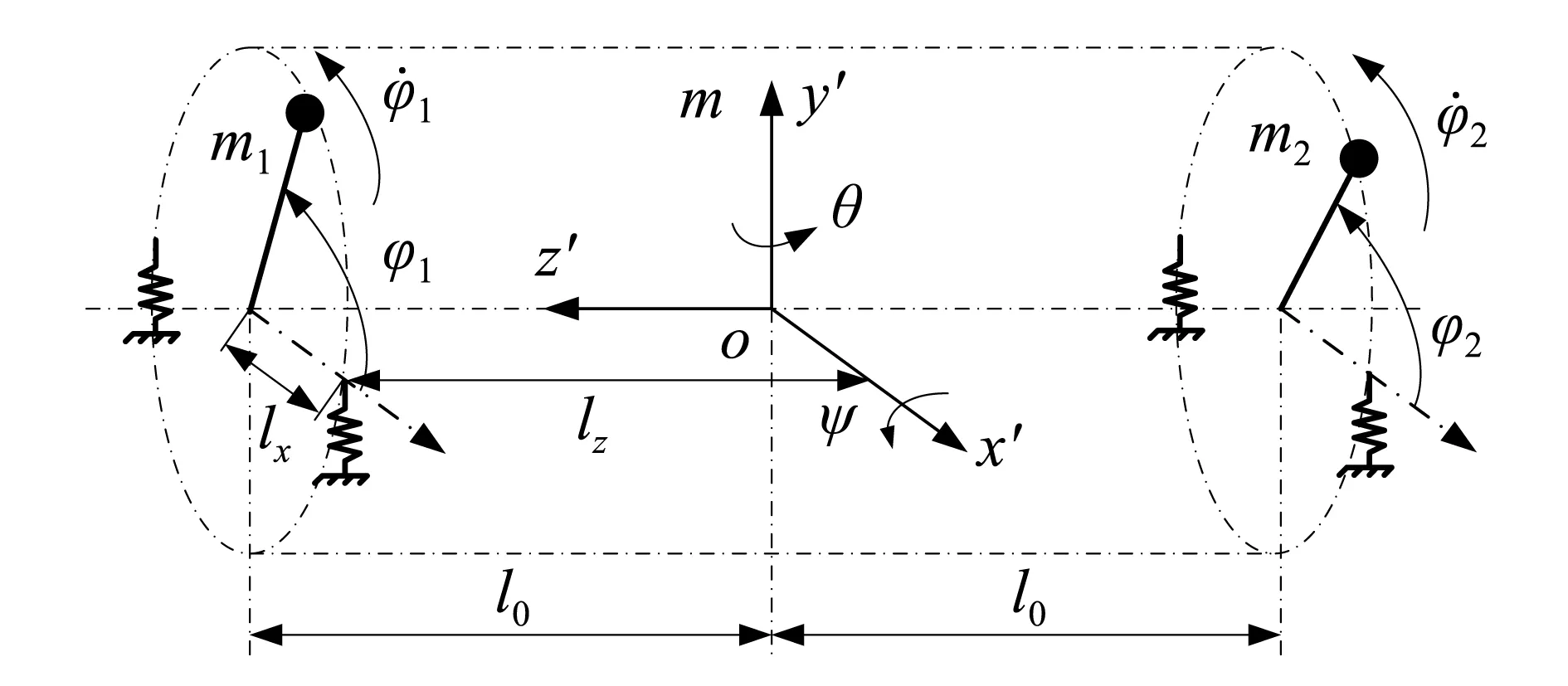
图1 两激振器同一旋转轴线振动系统的动力学模型Fig.1 Dynamic model of the vibration systemdriven by two exciters with same rotational axis

由振动系统的动力学模型可知，oxy为固定坐标系，其原点o为振动系统质心平衡点，振动体可产生4个方向的运动，分别为水平方向x的运动，竖直方向y的运动，绕x轴的ψ摇摆运动和绕轴y的θ摇摆运动。另外，两激振器分别绕电机轴旋转，由φ1和φ2来表示它们的运动。从而，振动系统共需要6个独立坐标才能确定其在空间的位置，即振动系统有6个自由度。选择x，y，ψ，θ，φ1和φ2作为广义坐标，求出振动系统的动能、势能和能量逸散函数，代入拉格朗日方程可得到振动系统的运动方程如下

(1)

2 自同步条件及其同步运动稳定性条件

2.1 振动系统的稳态响应

设两激振器的平均相位为φ，且激振器1超前激振器2的相位差为2α

φ1=φ+α,φ2=φ-α

(2)

由于振动系统的运动是周期性变化的，即两电机的外负载是周期性变化的，所以电机转子的角速度也是周期性变化的。取两激振器稳态时旋转周期的最小公倍数为T0，则在T0内两激振器的平均角速度一定为常数，可表示为

(3)

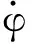
(4)

(5)

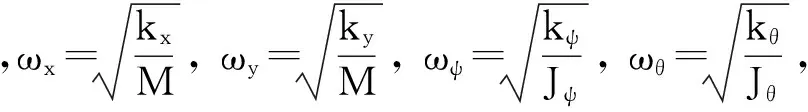
i=x,y,ψ,θ。

式中：ωi为系统i方向固有频率，ξi为系统i方向相对阻尼系数，π-γi为系统i方向响应的相位滞后角，i=x,y,ψ,θ；rm为偏心转子与机体总质量之比，η为两偏心转子之间质量比；lj为系统j方向当量回转半径，rj为系统偏心转子旋转中心距离质心的距离与系统j方向当量回转半径之比，j=ψ,θ。

2.2 两激振器的无量纲耦合方程

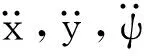
(6)

其中，

(7)

同步理论主要研究电机稳态时的自同步过程，由于本文试验机中的电机为直流电机，所以通常认为直流电机的电枢电压、励磁电流、电枢总电阻均为恒值。在此条件下根据他励直流电机的等效电路导出其电磁转矩方程，

(8)

式中：U为电源电压；R为电枢回路总电阻；Ke为电动势常数；Km为转矩常数；ω为转子转速。

设振动系统稳态时转子角速度ωm0产生慢变的微小波动量为ε，则转子实际角速度ω=(1+ε)ωm0，将其代入式(8)。电机的电磁转矩在ωm0附近进行泰勒级数展开并忽略高次项，则：

Te=Te0-ke0ε

(9)

根据式(9)，得到两电机在ωm0附近运行时的电磁转矩，

(10)

把式(7)和式(10)代入式(6)，然后将式(6)改写成矩阵形式，式(6)中的两个方程相加作为矩阵第一行，两个方程相减作为矩阵第二行，整理得：

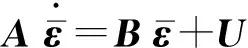
(11)

2.3 两激振器实现自同步的条件

(12)

其中，

TR1=Te01-fd1ωm0-TuWs0,
TR2=Te02-fd2ωm0-Tuη2Ws0

(13)

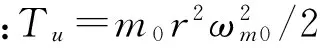
将式(12)中两项相减并整理得

(14)

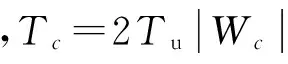
定义两激振器的同步力矩和作用在两电机上的负载力矩的比值为振动系统的同步能力系数Γ，

(15)

同步能力系数Γ表示同步力矩克服两电机电磁转矩实现同步的能力，当其值大于1时表示振动系统可实现振动同步运动，即一个电机停止电源供电，振动系统仍然可保持同步运动。

2.4 振动系统同步运动的稳定性

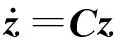
(16)

其中，C=A′-1B′，

通过C=A′-1B′求出矩阵C，进而通过det(C-λI)=0得到矩阵C的特征方程如下

λ3+c1λ2+c2λ+c3=0

(17)

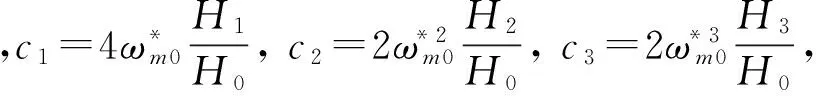
H1=ρ1κ2+ρ2κ1-WsWc,

H2=2κ1κ2+(ρ1+ρ2)Wccos 2α0+(ρ1-ρ2)Wssin 2α0+

H3=(κ1+κ2)Wccos 2α0+(κ1-κ2)Wssin 2α0+2WsWc。

在小阻尼的超远共振系统中，与Wc相比，表达式c1，c2和c3中的Ws很小甚至可以忽略。因此，忽略Ws后，H0，H1，H2和H3可以化简为，

(18)

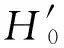
(19)

(20)

(21)

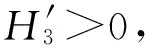
Wccos 2α0>0

(22)

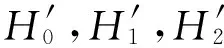
(23)

因为ρ1κ2+ρ2κ1>0，式(23)成立。

综上所述，式(19)情况满足Routh-Hurwitz判据条件，即振动系统同步运动的稳定性条件为Wccos 2α0>0。如果Wc>0，则2α∈(-90°,90°)时振动系统的同步运动状态是稳定的；同理，如果Wc<0，则2α∈(90°,270°)时振动系统的同步运动状态是稳定的。

3 数值讨论

根据第2节的讨论，本节将进一步给出一些定量的数值分析，具体参数见表1。

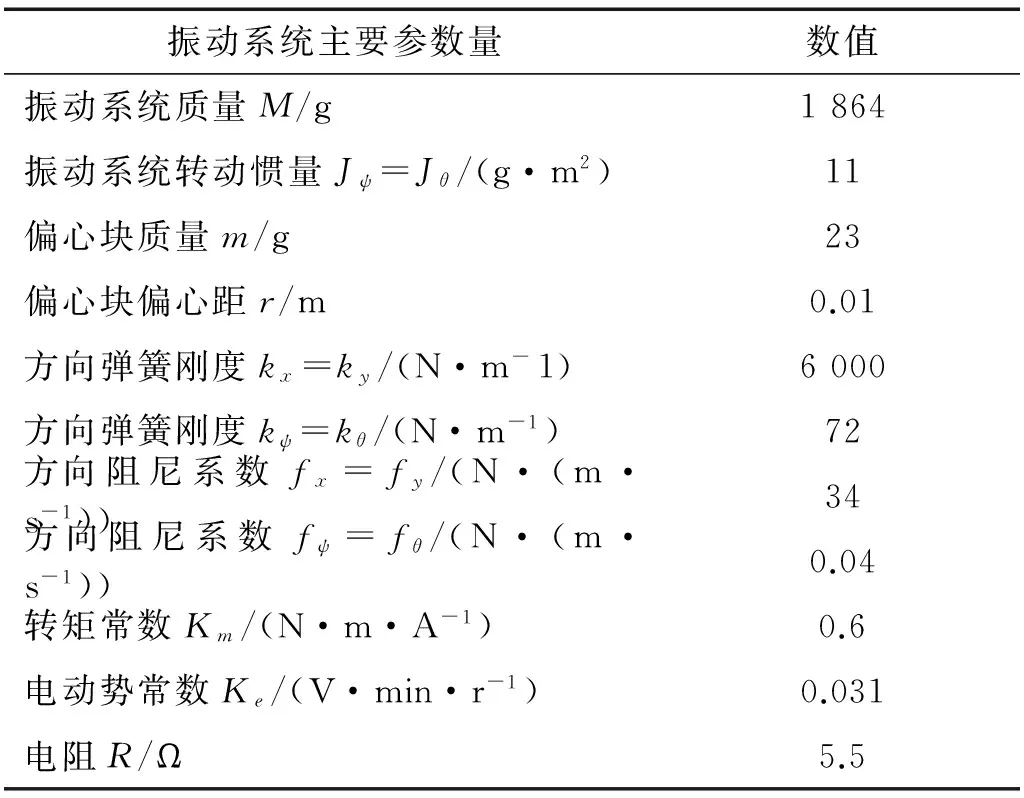
表1 振动系统仿真参数

由式(14)可知影响振动系统同步运动的主要参数包括Ws0和Wc，他们是无量参数rm，rψ，rθ，η，μx，μy，μψ和μθ的函数。由于在超远共振系统里μx，μy,μψ和μθ变化很小，接下来主要研究无量纲参数rm，rψ和η对同步运动的影响。

因为振动系统的稳定性条件为Wccos 2α>0，而且从无量纲参数Wc的表达式可以看出其随rψ的变化，Wc将出现一个零值点，所以Wc变化决定相位差2α的变化，这就是振动系统的选择运动耦合动力学特性。

图2表示η取不同值时相位差2α的比较。由图可知每种情况下相位差2α均在rψ=1附近发生值的转变。当系统结构参数完全对称时，即两激振器质径积相等时，随着rψ的增加，2α完成由180°到0°的转变。通过对比可知当系统结构参数完全对称时，2α越能更好的趋近180°和0°。可见，Wc值的正负将相位差2α分成二个区域。

图3表示η取不同值时同步力矩Tc的比较。由于同步力矩Tc是Wc和转子动能Tu的函数，如图所示每种情况下同步力矩Tc均有一个零值，而且该值均在rψ=1附近。在相位差2α趋于0°区域，随着rψ的增加同步力矩Tc逐渐变大。通过对比可知当系统结构参数完全对称时，同步力矩Tc的值最大，更容易实现两激振器间的同步运动。

图4表示η取不同值时同步能力系数Γ的比较。由于同步能力系数Γ是Wc，Ws0和Ws的函数，而Wc，Ws0和Ws又是rm的函数，所以rm并不影响同步能力系数Γ。同上，由图可知每种情况下同步能力系数Γ均有一个零值，而且该值均在rψ=1附近。随着rψ的值接近1，同步能力系数逐渐变小。通过对比可知当系统结构参数对称性越好，同步能力系数的值就越大。

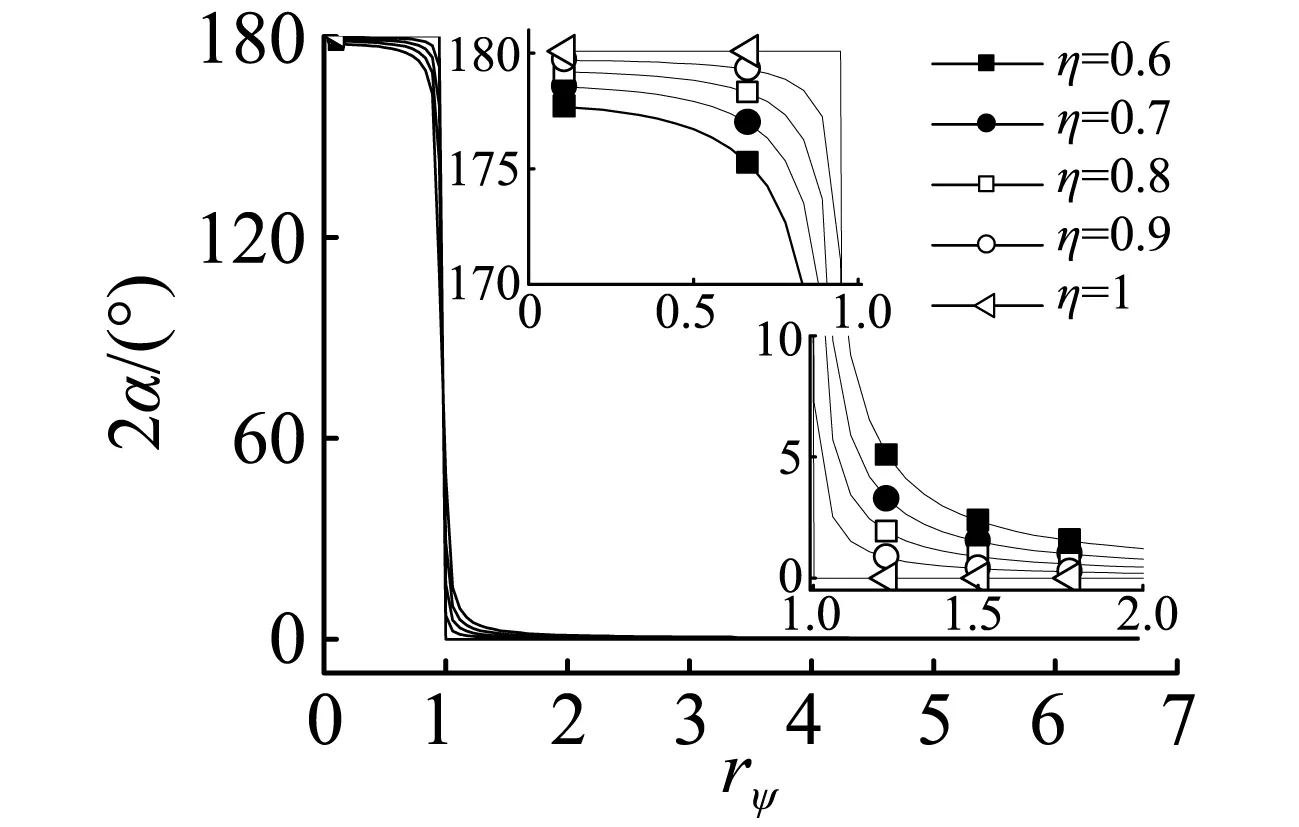
图2 相位差角与系统结构参数的关系Fig.2 Relation between the phase difference and the structural parameters

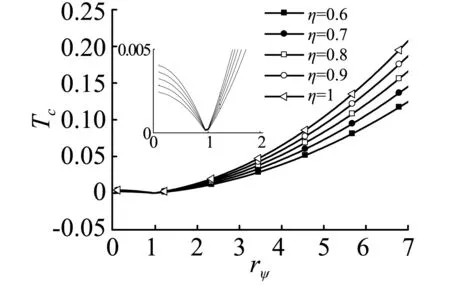
图3 同步力矩与系统结构参数的关系Fig.3 Relation between the synchronization torque and the structural parameters

图4 同步能力系数与系统结构参数的关系Fig.4 Relation between the coefficient of synchronization ability and the structural parameters

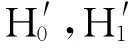
图5 同步运动稳定性参数与系统结构参数的关系Fig.5 Relation between the parameters of synchronization operation stability and the structural parameters

4 试验分析

在本节中，将通过两组试验用以对上述理论和数值结果，进而验证所用方法的合理性。振动试验台结构如图6所示，两台振动直流电机对称地安装在振动体上，振动体通过弹簧连接固定在支架上。图中数字1为电机，2为激振器，3和4为加速度传感器，5为弹簧组。信号采集使用丹麦B&K公司3650D采集前端，数据后处理应用pluse reflex软件。试验台的结构参数如表1所示。

图6 双机同向回转振动球磨机的动力学模型Fig.6 Dynamic model of the vibration mill driven by two exciters in the same direction

4.1 两激振器安装距离较近情况下试验结果

当两电机工作电压设定为7 V时，两激振器间距离为，2l0=7 cm。振动机实测数据，如图7所示。

图7(a)为两电机转速。在开始几秒后，两电机实现同步运动，在15 s附近，将电机2的电源切断，然后1 s后接通，两电机再次实现同步运动。图7(b)为两激振器间的相位差，当两电机实现同步运动后，相位差接近180°。当遇到断电干扰后，相位差发生振荡；当电机2接通电源后，相位差再一次稳定在180°附近。图7(c)和7(d)为质心处x和y两方向的振幅。同样7(e)和7(f)为振动系统最远端位置处(图6中数字4所指位置)x和y两方向的振幅。对比两位置点的振幅可知，当两激振器间的相位差处于180°附近，振动体实现空间绕z轴的圆锥运动，而且当出现干扰时，机体呈现不规则运动。

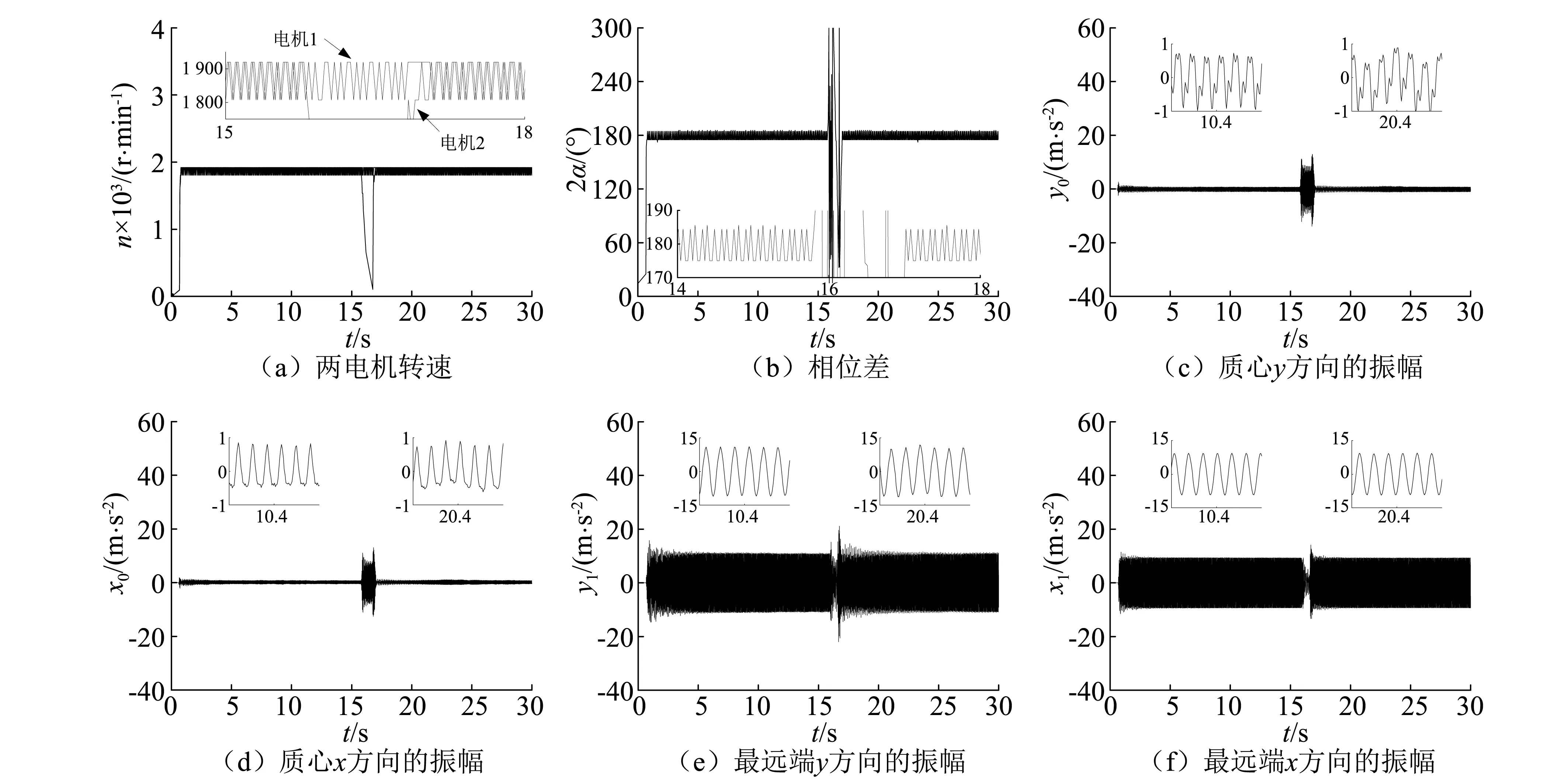
图7 两激振器安装距离较近的情况下试验结果，2l0=7 cmFig.7 Experiment results of the smaller distance between the two exciters，2l0=7 cm

4.2 两激振器安装距离较远情况下试验结果

如图8所示，两激振器间距离为，2l0=17 cm。试验方案同图7。两电机实现同步运动后，相位差接近0°， 对比两位置点的振幅可知，当相位差处于0°附近时，振动体实现空间绕z轴的圆周运动。

以上两组试验很好地验证了理论分析和数值结果的正确性，即Wc>0，振动系统选择相位差趋于0°的空间圆周运动；同理，如果Wc<0，振动系统选择相位差趋于180°的空间圆锥运动。

图8 两激振器安装距离较远的情况下试验结果，2l0=17 cmFig.8 Experiment results of the longer distance between the two exciters，2l0=17 cm

5 结 论

(1)采用拉格朗日方法建立两激振器同一旋转轴线振动系统的动力学模型。应用小参数平均法获得两激振器的无量纲耦合方程，进而将该类振动系统的同步问题简化为小参数平均微分方程零值解的存在与稳定性的问题。

(2)根据耦合方程零解存在的条件得出了振动系统实现自同步的同步性条件，即振动系统的同步力矩大于或者等于两电机剩余电磁转矩差的绝对值。应用Routh-Hurwitz判据得到了振动系统同步运动的稳定性条件，即Wccos 2α0>0，Wc值的正负决定两激振器同步运动时相位差的稳定域。

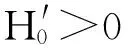
(4)通过对试验机的试验，验证了理论分析的正确性。即在远共振工作状态下，当激振器的旋转中心距离振动系统质心的距离大于机体的当量回转半径时，振动系统实现相位差为0°的空间圆周运动；反之，振动系统实现相位差为180°的空间圆锥运动。

[1] BLEKHMAN I I. Self-synchronization of vibrators in some types of vibrational machines[J]. Inzhenerny Sbornik, 1953, 16: 49-72.

[2] 闻邦椿，刘凤翘. 振动机械的理论及应用[M]. 北京：机械工业出版社，1982.

[3] ZHAO Chunyu, ZHU Hongtao,WANG Ruizi, et al. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of linear motion. Part I:Theoretical analysis[J]. Shock and Vibration, 2009, 16(5): 505-516.

[4] ZHAO Chunyu, ZHAO Qinghua, ZHANG Yiming, et al. Synchronization of two non-identical coupled exciters in a non-resonant vibrating system of plane motion[J]. Journal of Mechanical Science and Technology, 2011, 25(1):49-60.

[5]DIMENTBERG M, COBB E, MENSCHING J. Self-synchronization of transient rotations in multiple shaft systems[J]. Journal of Vibration and Control, 2001, 7(2): 221- 232.

[6] PALACIOS J L, BALTHAZAR J M , BRASIL R M L R F. A short note on a nonlinear system vibration under two non-ideal excitations[J], Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2003, 25(4):391-395.

[7] BALTHAZAR J M. Short comments on self-synchronization of two non-ideal sources supported by a flexible portal frame structure[J]. Journal of Vibration and Control, 2004, 10(2):1739-1748.

[8] DANUTA S, MACIEJ K. Nonlinear oscillations of a coupled auto parametrical system with ideal and nonideal sources of power[J]. Mathematical Problems in Engineering, 2006,834(1): 369-376.

[9] 杨万东,马建敏,刘颖，等.同一轴线上双激振器驱动的振动体同步运动状态分析[J]. 振动与冲击,2008,27(6): 7-10.

YANG Wandong, MA Jianmin, LIU Ying, et al. Synchronous movement analysis of a vibrating body driven by double vibrators in the same axis[J]. Journal of Vibration and Shock, 2008, 27(6): 7-10.

[10] MIKLOS A, SZABO Z. Vibrator with DC motor driven eccentric rotors[J]. Periodica Polytechnica Mechanical Engineering, 2012, 56: 49-53.

[11] MIKLOS A, SZABO Z. Mechanical synchronation in dual-rotor vibroactuator[J]. Proceedings in Applied Mathematics and Mechanics, 2013, 13: 41-42.

[12] MIKLOS A， SZABO Z. Simulation and experimental validation of the dynamical model of a dual-rotor vibrotactor[J]. Journal of Sound and Vibration, 2015, 334: 98-107.

Self-synchronization theory about two exciterson the same rotational axis in a vibration system

CHEN Xiaozhe1,2, DOU Jingxin1, KONG Xiangxi1, WEN Bangchun1

(1. School of Mechanical Engineering and Automation， Northeastern University， Shenyang 110819, China;2. School of Control Engineering, Northeastern University, Qinhuangdao 066004, China)

The self-synchronization theory about two exciters with the same rotational axis in a vibration system was studied. The motion equation of the vibration system was derived by applying the Lagrange equation. By introducing the average method of small parameters, a dimensionless coupling equation for the two exciters was deduced, which converts the synchronous problem of this type vibration system into the existence and stability of zero solutions of the dimensionless coupling equation. The synchronization condition of the two exciters carrying out synchronization motion was obtained from the existence of zero solutions, and the stability condition was acquired according to the principle of Routh-Hurwitz. By analyzing the selection motion characteristics of the vibration system, it is concluded that when the distance between the rotating center of the exciters and the mass center of the vibration system is greater than the equivalent radius of the vibration system, the vibration system can carry out a spatial circle motion with 0 degree phase difference, otherwise it can carry out a spatial cone motion with 180 degree phase difference. The correctness of the theoretical analysis was verified by experiment.

self-synchronization; synchronization condition; synchronization stability; phase difference

国家自然科学基金(51375080)

2015-12-17 修改稿收到日期： 2016-06-06

陈晓哲 男，博士，讲师，1986年生

闻邦椿 男，教授，博士生导师，中科院院士，1930年生

TH113

A

10.13465/j.cnki.jvs.2017.14.003