圆管柱-H型钢梁3种不同形式节点的抗震性能研究

董锦坤，仝 芳，袁少林

（辽宁工业大学 土木建筑工程学院，辽宁 锦州121001）

圆管柱-H型钢梁3种不同形式节点的抗震性能研究

董锦坤，仝 芳，袁少林

（辽宁工业大学 土木建筑工程学院，辽宁 锦州121001）

通过运用ABAQUS有限元软件对中柱、边柱、角柱3种不同形式的圆管柱-H型钢梁连接点，进行低周往复荷载的加载，研究3种不同节点抗震性能的优劣。采用应力云图、滞回曲线、骨架曲线、延性系数、耗能能力、刚度退化以及强度退化等抗震性能指标分析其抗震性能。

抗震性能；ABAQUS有限元；滞回曲线；骨架曲线

随着我国对钢管、工字钢、钢板等钢结构的大量生产和使用，钢结构在建筑中所扮演的角色愈来愈重要，钢框架结构中关于圆管柱与H型钢梁连接节点的研究必将成为国内研究的热点课题。由于地震给社会带来的的危害不能准确地预测，能做的就是房屋对地震的预防即抗震设防，所以对该类节点的抗震性能的研究是必要的。通过现有的研究总结发现圆管柱-H形钢梁连接节点的连接形式中的无拐点圆弧形外环板连接形式的节点能有效避免应力集中，提高结构的抗震性能。

日本是一个地震多发国家，在抗震方面有着较为深入的研究及雄厚的经验，许多关于抗震方面的规范值得借鉴，其中《钢结构接合部设计指针》[1]和《冷成型方钢管设计施工手册》[2]2本规范中，对圆管柱-H型钢梁节点的隔板贯通式连接构造细节做了详细规定，对于圆管柱-H型钢梁节点其他形式的连接研究并不透彻，同时我国只在《多、高层民用建筑钢结构节点构造详图》中对菱形外环板的此种类型的节点情况有一些规定[3]。相对来说，对管柱-H形钢梁连接节点的连接形式中无拐点圆弧形外环板连接形式抗震性能的研究具有重要的意义。

本文利用ABAQUS有限元分析软件对圆管柱-H型钢梁平滑过渡无拐点外环板连接式的边柱、中柱、角柱3种不同的连接形式的节点，在低周往复荷载作用下的抗震性能进行对比研究。可为3种不同的节点形式在工程设计以及工程实际应用中提供些许参考。

1 节点设计

1.1 节点模型的几何尺寸

本文建立的有限元模型已经经过有关研究者进行的实验与模拟比较分析，证明了该模型的正确性，准确性以及可行性。本文主要对圆管柱-H型钢梁刚性连接点的中柱、边柱、角柱进行循环往复荷载下的抗震性能研究，并进行对比研究分析。为了更准确地研究各个不同节点的抗震性能，首先要确定节点模型的几何尺寸，建立模型，在此基础之上进行循环往复荷载的加载及相关研究。节点模型的几何尺寸如表1。

表1 节点模型的几何尺寸 mm

D为圆柱外直径，tc为柱厚度，bsr为加劲肋长度，tsr为加劲肋厚度，ts为外环板厚度，hs为外环板宽度，r为外环板上圆弧半径，另外，剪切板宽度a=175 mm，长度l=605 mm。

1.2 节点模型的受力加载

加载方式如图1～图3，柱顶所施加的轴向压力P，本文采取面荷载加载方式，大小为100 MPa（P=αAfy，轴压比α=0.3）。本文加载制度采用15级位移振幅，依次为±0.15，±0.2，±0.25，±0.3，±0.35，±0.4，±0.45，±0.5，±0.6，±0.7，± 0.8，±0.9，±1.0，±1.1，±1.2，前两级加载循环2次，后十三级加载循环1次。本文采用在与X同方向上的梁端施加对称荷载，在与Y同方向上的梁端施加相反的对称荷载方式，具体加载方向及约束方式如图1。

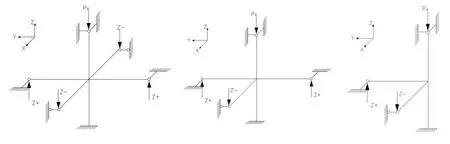
图1 外荷载加载方式

Z向位移幅值大小的确定：

《建筑抗震设计规范》(GB 50011—2010)[4]中指出：多、高层钢结构弹性层间位移角不得超过1/250；塑性层间位移角不得超过1/50；如图1，位移幅值与层间位移角的计算关系如下

式中：Δ为位移幅值；θc为层间位移角；θb为梁端转角；L为梁长，1.325 m。

由上述规范可知，则mm=26.5 mm。

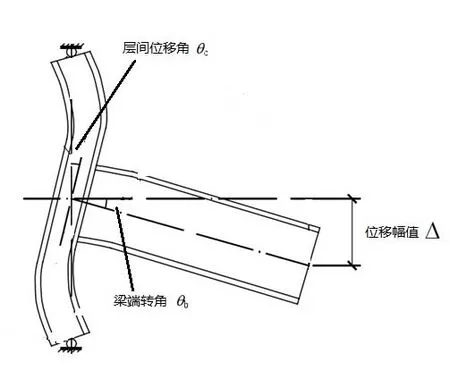
图2 节点图

那么本文的Z向位移幅值最大不得大于2.65cm，为了研究其承载能力大小，模型必须达到破坏，为使模型达到破坏状态，Z向位移幅值必须大于其限值，本文取4 cm。本文采用的是Q345钢，材料属性以及外加荷载值的大小如表2。

表2 材料属性及荷载

1.3 节点模型的建立及网格划分

本文所采用的有限元模型由梁、柱、外环板、剪切板以及加劲肋组成，采用栓焊混接刚性连接，即外环板和加劲肋与柱采用焊接连接，梁的上下翼缘与外环板采用焊接连接，腹板与加劲肋采用螺栓连接，不考虑焊缝以及残余应力产生的影响，忽略螺栓变形，通过ABAQUS有限元软件建立的中柱、边柱、角柱模型如图3。

网格的划分中，为使各个实体间的相互接触面可以相互适应，本文采用的是结构优化网络技术（Structured），统一采用以六面体单元（Hex）为主的网格，采用C3D8R3维实体单元类型，在划分梁时将梁的上翼缘、腹板以及下翼缘进行拆分后划分网格，从而使网格质量提高，更便于得到更精确的计算结果。各个节点的网格划分图如图4。

图3 中柱、边柱、角柱模型

图4 中柱、边柱、角柱网格模型

梁、柱、外环板、加劲肋以及剪切板之间的相互作用采用绑定约束用来模拟焊接连接；梁端面须设置一参考点，并与梁端采用耦合约束，将力施加在参考点上，从而控制梁端的位移。

2 能分析节点抗震性

本文将通过低周往复荷载作用下的应力云图、滞回曲线、骨架曲线、节点延性系数、承载力下降系数以及等效粘滞系数来分析中柱、边柱、角柱3种不同节点的抗震性能，为节点设计以及在工程中的应用提供些许参考。

2.1 应力云图

本节对中柱、边柱、角柱梁端的应力云图进行分析比较，如图5。

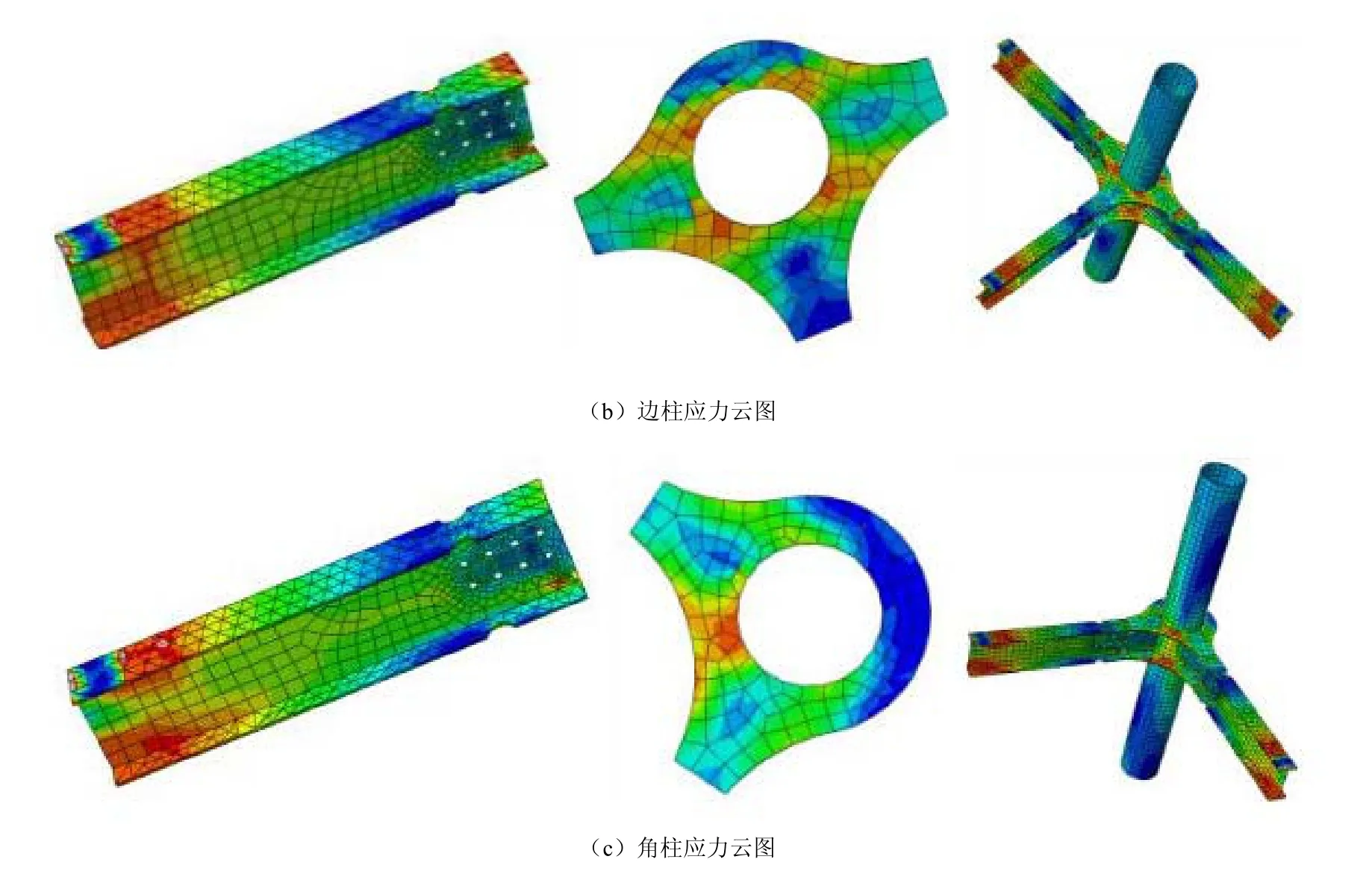
图5 应力云图

图5为3种不同节点的应力云图，由图5可知，在与X同方向上的梁端施加对称荷载，在与Y同方向上的梁端施加相反的对称荷载，使得每两相邻梁端承受相反方向的荷载，导致在3种不同节点的相邻2个梁中间的外环板上的应力值增大，产生了较为明显的塑性变形。在梁端承受往复荷载区域，上、下翼缘与腹板相交处应力值呈现较大值，此处的塑性变形最为明显，由于梁上削弱区的存在，使得梁与外环板相交处应力值相对较低，很好地将梁端塑性铰转移至梁上，从而增大了节点处的承载能力。从图上还可以看到整个圆管柱柱壁的应力值分布从节点域向两端逐渐减小，并且相对于梁端与外环板应力值要小很多。

下面通过表3具体数值进行3种不同节点的分析。

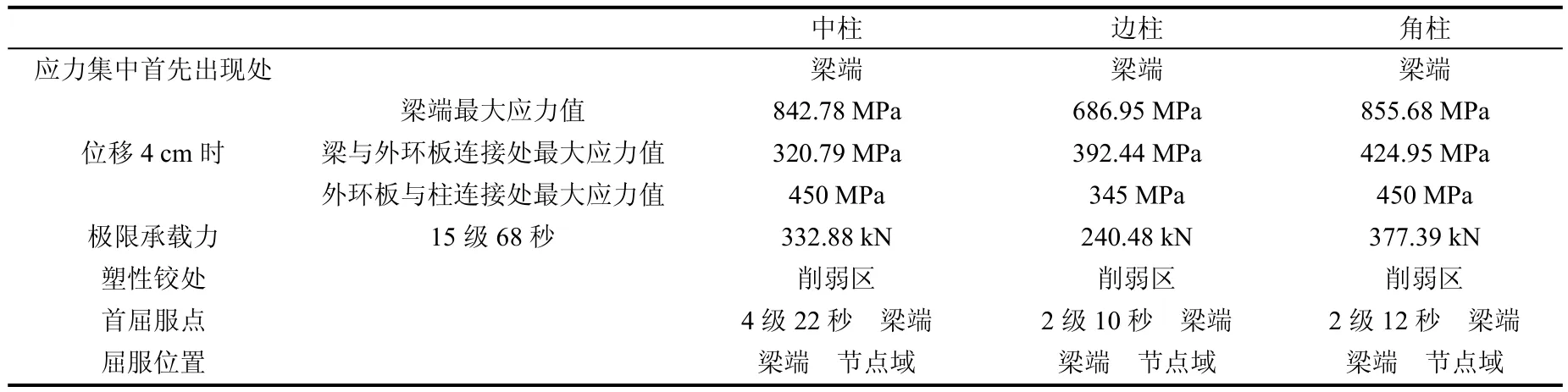
表3 加载现象

通过对表3加载现象的分析对比，得出以下几点结论。

(1)应力集中首先出现处均在梁端。

(2)当加载循环往复荷载到最大位移时，3种节点中梁端应力均最大，节点域最大应力在梁端最大应力的49.7%～57.1%范围内。另外，中柱梁端最大应力大于边柱，小于角柱；节点域的最大应力中柱大于边柱，小于角柱。

(3)3种不同节点的塑性铰均出现在梁端削弱区，表明削弱区的存在符合理论，成功将梁端塑性铰转移至梁上，提高了节点处的承载力。

(4)3种节点的首屈服点均发生在梁端，屈服位置均为梁端与节点域。而首屈服点出现的时间边柱最早，角柱次之，中柱最晚。

综合以上对比分析，在进行中柱、边柱、角柱设计时，可采取有效措施加强边柱的承载能力。

2.2 滞回曲线

本节对中柱、边柱、角柱梁端的位移-力滞回曲线进行分析比较，讨论3种不同节点的抗震性能的不同，图6为滞回曲线。

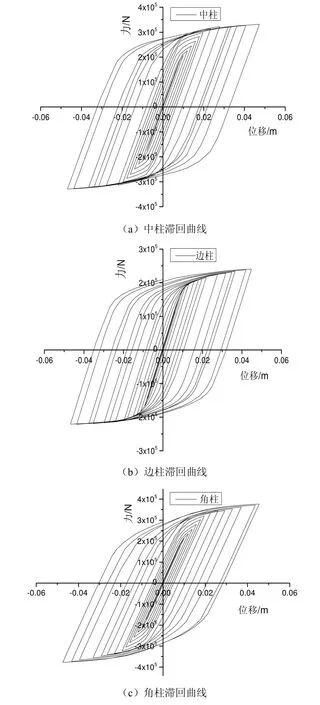
图6 滞回曲线

由图6滞回曲线可以看出：3种节点的滞回曲线形状均饱满圆滑，成梭形，说明3种节点在短时间内吸收的能力均较强，均具有较好的耗能能力。通过对比3种不同节点的极限荷载可知，中柱的极限荷载大于边柱的极限荷载，而小于角柱的极限荷载。

在加载初期1～5个循环内，加载时的位移-力曲线呈直线上升，当卸载时又呈直线下降趋势，当荷载回到零点时，位移值基本为零，没有产生残余应力，说明构件处于弹性阶段，且构件的刚度基本不变。随着位移值的进一步加大，在第6～10个循环内，位移-力曲线不再呈直线形式，而是开始向位移轴方向倾斜，滞回环的面积也随之增大，当位移再次回到零点时，力的值却不再为零，而是具有一定的值，表明构件开始进入弹塑性阶段，构件发生了一部分不可逆转的塑性变形。随着位移的不断增大，在11～17个循环内，滞回环的面积进一步加大，位移回到零点时，反力的值同样在逐渐变大，表明构件进入了塑性阶段，构件的整体刚度在逐渐降低，且每次卸载后的残余应变在不断增加，当构件达到极限荷载后，构件的塑性变形越来越大，导致节点承载能力迅速降低。

2.3 骨架曲线

对中柱、边柱、角柱梁端的位移-力滞回曲线进行分析比较，图7即为骨架曲线。

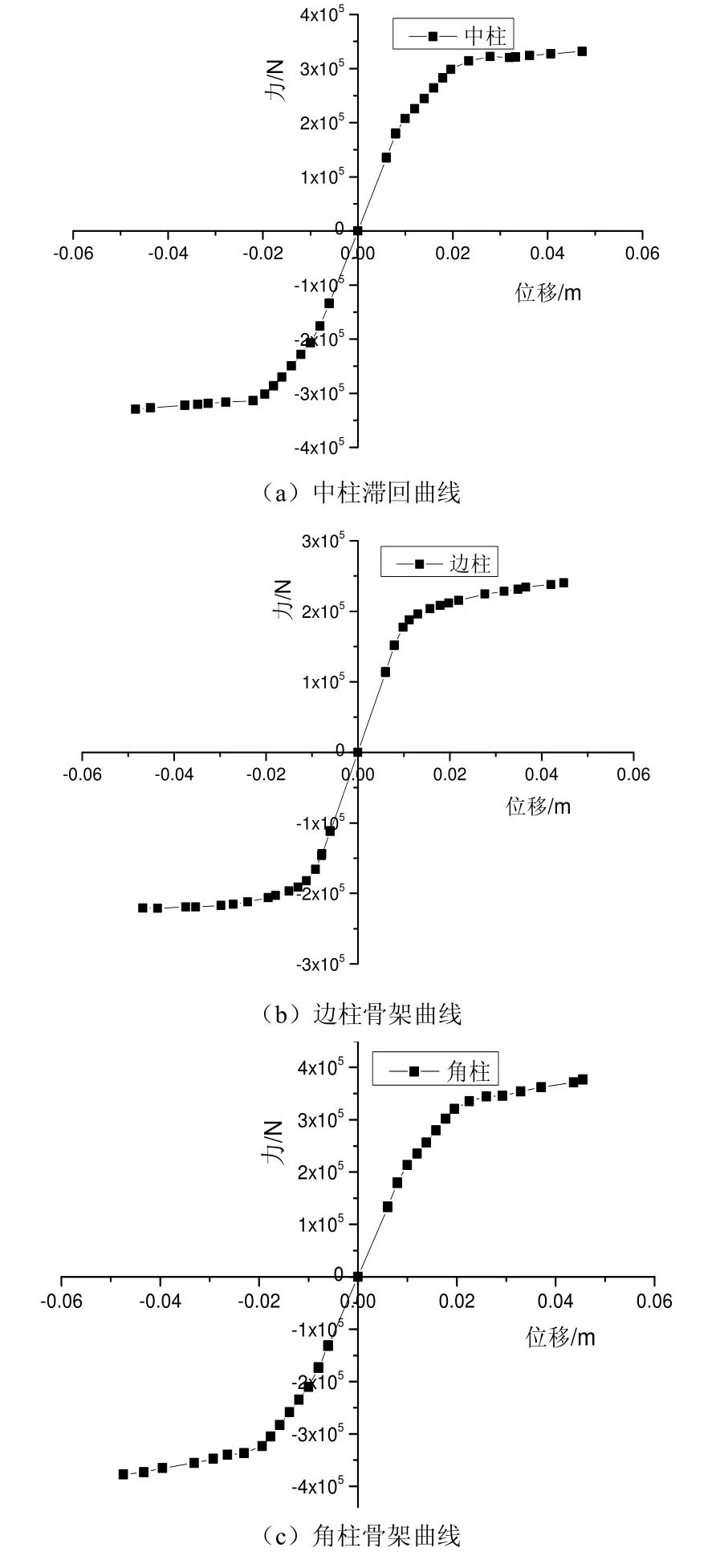
图7 骨架曲线

通过3种不同的节点的骨架曲线可知，在整个荷载的加载过程中，3种节点均经历了直线弹性阶段，在此阶段材料的刚度值恒定不变，没有出现残余应变，且边柱的弹性阶段时间要明显小于中柱和角柱的弹性阶段时间。在弹性阶段之后的非线性弹塑性阶段中，随着往复荷载逐渐增加，节点的塑性变形也在不断加大，其中，边柱节点的塑性变形要大于边柱和角柱。

通过骨架曲线的对比，很明显的可以看出，边柱的极限承载力最低，角柱的极限承载力最好，中柱的极限承载力仅次于角柱。另外，边柱的屈服极限最低，角柱的屈服极限最高，中柱的屈服极限仅次于角柱。再者，边柱的屈服位移最小，角柱的屈服位移最大，中柱的屈服位移仅次于角柱。

2.4 延性性能

通常用延性系数μΔ来评判结构或构件的延性的好坏，延性系数μΔ越大，表示节点的延性性能越好，表明其抗震性能越好。延性系数公式：

式中：μΔ为延性系数；Δu为极限位移（采用结构达到极限荷载后的0.85倍的极限荷载值所对应的位移值）；Δy为屈服位移。

对于确定屈服位移Δy，本文采用以下方法取得，参照图8，具体如下：用直线连接坐标原点O和0.6倍的极限荷载所对应的点A（极限荷载出现以前），并延长使之与uP对应的直线相交于B点，过B点向X轴做垂线，垂足即为屈服位移Δy[5]。

根据以上方法求得延性位移系数，见表4。

表4 延性位移系数求解结果

图8 屈服位移求解示意图

从表4中的数据明显可以看出，边柱的延性位移系数最大，中柱次之，角柱延性位移系数最小。总的来说，3种节点的延性性能均较好，相比之下，边柱的延性性能最好，中柱次之，角柱的延性性能最差。

2.5 耗能能力

节点耗能能力可以采用等效粘滞阻尼系数he来评价，等效粘滞阻尼系数he越大，节点耗能能力越强。等效粘滞阻尼系数确定的公式[6](3)以及示意图9。

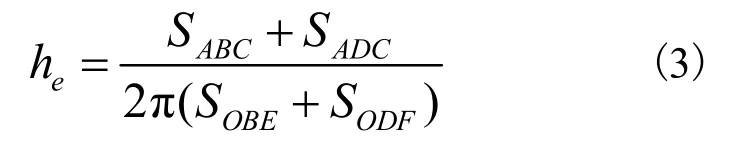
图9 等效粘滞阻尼系数公式计算图

其中，SABC+SADC表示滞回环的面积，SOBE+SODF表示三角形OBE和三角形ODE的面积之和。根据上述方法求得3种不同节点的等效粘滞阻尼系数列于表5中。

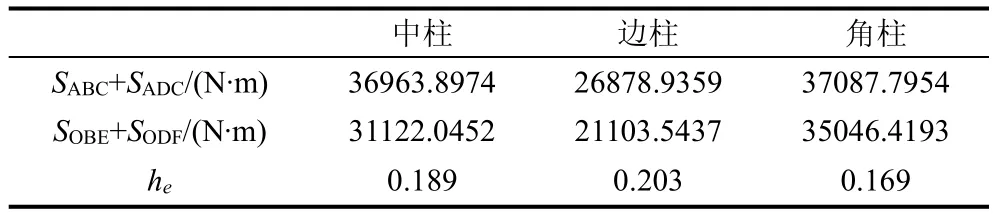
表5 等效粘滞阻尼系数求解结果

根据表5中的数据，可以明显看出边柱的等效粘滞阻尼系数最大，中柱次之，角柱最小，表明边柱的耗能能力最好，中柱次之，角柱的耗能能力是3种节点中最差的。

2.6 强度退化

强度退化通俗来讲就是随着循环往复荷载的加载，构件的承载力不断降低的现象，通常用承载力降低系数来评价构件的强度退化标准。承载力降低系数的计算公式[7]如下：

根据上述方法求得3种不同节点的承载能力下降系数列于表6中。

表6 承载能力下降系数求解结果

强度的退化以承载能力的下降系数为评价标准，承载能力下降系数越大，强度的退化就越快。由表6可以看出，角柱的承载能力的下降系数最大，中柱次之，边柱的承载能力的下降系数最小，故而，角柱的强度退化速度最快，中柱次之，边柱的强度退化速度相对来讲是最慢的。

3 结论

通过对3种不同节点的抗震性能指标分析可得如下结论。

(1)节点的设计基本上达到了“强柱弱梁，强节点弱构件”的抗震设计理念，而且梁端削弱区的存在提高了节点域的抗震性能。

(2)角柱梁端最大应力最大，中柱次之，边柱的梁端最大应力还要小于中柱；节点域的最大应力中柱大于边柱，小于角柱。

(3)3种节点在短时间内吸收的能力均较强，均具有较好的抗震性能和较好的耗能能力。角柱的极限荷载和极限承载力最大，边柱次之，中柱的极限荷载和极限承载力要略小于角柱。

(4)3种节点的延性性能均较好，相比之下，边柱的延性性能、耗能能力最好，强度退化速度最慢，中柱次之，角柱的延性性能、耗能能力最差，强度退化速度也最快。

总的来讲，该设计节点的3种不同形式的节点抗震性能均较强，相比之下，角柱的极限承载力最大，在短时间内吸收的能力最强，而其延性、耗能能力是最弱的，强度退化最快。边柱则与角柱相反，其延性、耗能能力是最强的，强度退化也是最慢的，但是也存在一定的不足，其极限承载力确是3者中最小的，短时间内吸收的能力最弱。中柱的各项指标则介于两者之间且偏于安全。在实际工程应用中，可针对各个不同节点形式的不足之处予以加强，以达到有效加强节点抗震性能的效果。

[1]日本建筑学会.钢结构接合部设计指针[M].东京:日本建筑学会出版社丸善株式会社,2001.

[2]日本建筑中心.冷成型方钢管设计施工手册[M].东京:日本建筑学会出版社丸善株式会社,2003.

[3]中国建筑标准设计研究所.多、高层民用建筑钢结构节点构造详图[M].北京:中国建筑工业出版社,2007.

[4]中华人民共和国住房和城乡建设部.GB 50011—2010.建筑抗震设计规范[S].北京:中国建筑工业出版社, 2010.

[5]徐绩青.延性系数确定方法讨论[J].水运工程,2004, 368(9):14-17.

[6]王燕.钢结构新型延性节点的抗震设计理论及其应用[M].北京:科学出版社,2012.

[7]朱伯龙.结构抗震实验[M].北京:地震出版社,1989.

责任编校：孙 林

Seismic Performance Research in Three Different Forms of Round The String-H Steel Beam Node

DONG Jin-kun,TONG Fang,YUAN Shao-lin

（Civil Construction Engineering College,Liaoning University of Technology,Jinzhou 121001,China）

The different seismic performance of three different nodes is studied by using the finite element softwareABAQUS in three different forms(middle column,side column and corner column)of round pipe string-H type steel beam connection point,for loading of low cycle loading.The seismic performance is analyzed through several seismic performance index such as the stress nephogram, hysteresis curves,skeleton curves,ductility,energy dissipation,stiffness degradation and strength degradation.

seismicperformance;ABAQUSfinite elementsoftware;hysteresis curve;skeletoncurve

TP35；TP38

A

1674-3261(2017)01-0052-07

2015-10-19

董锦坤(1969-)，男，辽宁锦州人，教授，博士。

10.15916/j.issn1674-3261.2017.01.014