拉胀三明治梁在爆炸载荷作用下的动态力学性能研究

崔世堂, 倪小军, 张 科

(1.中国科学院材料力学行为和设计重点实验室 中国科学技术大学， 合肥 230026;2.中国科学院等离子体物理研究所， 合肥 230031)

拉胀三明治梁在爆炸载荷作用下的动态力学性能研究

崔世堂1, 倪小军2, 张 科1

(1.中国科学院材料力学行为和设计重点实验室 中国科学技术大学， 合肥 230026;2.中国科学院等离子体物理研究所， 合肥 230031)

通过数值方法考察了芯层采用负泊松比蜂窝的三明治梁在爆炸载荷作用下的动态力学响应和能量吸收能力。采用在三明治梁面层施加均匀载荷的方式代替爆炸载荷，在相同面密度的前提下，就背板的最大位移和复合梁的能量耗散问题和实体梁进行了对比，并对复合梁的面板和芯层进行了参数化设计。设计参数包括胞壁厚度、前面板的厚度、胞元扩张角。在爆炸载荷作用下，和实体梁相比，复合梁可以降低背板最大位移，延迟背部面板到达最大速度时的时间，吸收更多的能量。

拉胀；负泊松比；三明治梁；有限元仿真

现代工程技术的发展不断需要具有特殊力学性能的新材料，这类材料通常具有独特或与直观现象相反的行为。具有负泊松比效应的“拉胀”材料，在受到单轴拉伸时会发生侧向膨胀，伴随着这种独特的拉伸和膨胀现象，具有负泊松比效应的材料展示出更强的物理和力学特性[1-2]。Lakes等[3]对拉胀铜泡沫和传统的铜泡沫进行了实验后发现，和传统泡沫相比，拉胀泡沫具有更高的屈服强度，更低的刚度，冲击时能吸收更多的能量。Bezazi等[4]用试验方法对负泊松比泡沫和传统泡沫进行了静态和疲劳测试，拉伸测试结果表明，负泊松比泡沫失效时的应力和应变分别为为正泊松比泡沫的1.7倍和2.6倍。张新春等[5]研究了具有负泊松比效应蜂窝材料的面内冲击问题，发现在名义应变一定的条件下提高冲击速度，材料表现出更强的能量吸收能力。正是由于拉胀多孔材料具有更高的冲击阻抗及较好的能量吸收能力等优点，在作为三明治结构的夹芯材料方面具有很大的应用潜力。

三明治夹芯结构在强冲击载荷作用下，芯层可呈现一应力几乎恒定不变的大的塑性变形过程, 大量的能量被转变为塑性变形能，有效的降低了透射到背板上冲击波的强度，提高了结构的能量吸收效率。有关多孔金属夹芯梁、板在准静态压力和低速撞击作用下的研究成果较多[6-8]。芯层的选择也从起初的泡沫铝发展到波纹板、蜂窝结构、Y型框架等其他样式[9-13]。研究表明，在同等面密度下，经过优化设计的轻质夹芯结构能够承受更强的爆炸冲击波，有较好的吸能效果。

目前，对于具有负泊松比蜂窝材料的研究已经展开，但主要集中于静态和准静态力学特性的讨论[14-16]，而对于负泊松比材料在极端加载条件下的研究并不多。卢子兴等[17]研究了四边手性蜂窝面内的动态压溃行为。Ma等[18]提出了一种采用功能梯度拉胀芯层的三明治抗爆结构。Schenk等[19]研究了芯层采用多层折叠的拉胀材料的三明治梁在准静态和脉冲加载条件下的的力学行为。Imbalzano[20]采用数值方法研究了爆炸载荷作用下拉胀复合板的吸能效率，与相同面密度的实体板相比，拉胀复合板可以减低背板的挠度，吸能效率更高。

本文中采用数值模拟方法，对爆炸载荷作用下芯层采用负泊松比蜂窝的三明治梁背板最大位移及能量吸收等动力学响应特性展开研究，考察面板厚度、胞元扩张角、胞元厚度等参数对吸能特性的影响，并与实体梁的冲击力学行为进行了对比，为进一步研究拉胀芯层的三明治梁、板的动态力学行为奠定基础。

1 计算模型

1.1 有限元模型

拉胀复合梁的芯层由具有相同壁长和壁厚的内凹六边形胞元组成，如图1(a)所示。胞元的扩张角θ控制在0°～30°，需要说明的是，当胞元扩张角为30°时，变为规则的三角形结构，不属于本文的研究范畴。

有限元模型如图1(b)所示，拉胀复合梁两端均为固定约束，梁的跨度2L=200 mm，宽度为B=10 mm，上下面层的厚度h=2 mm。面层和芯层材料的杨氏模量Es=200 GPa，泊松比μ=0.3，屈服应力σys=300 MPa，材料的密度ρs=8 000 kg/m3，采用有限元软件ABAQUS/Explicit进行数值模拟，不考虑材料的应变率效应[21]。计算中采用1/2对称模型，面层采用solid单元，芯层采用shell单元，为保证收敛，沿厚度方向取5个积分点。计算中可能的接触，均采用自动接触算法，所有的摩擦均不计。为了获得胞元每个棱边合适的单元数量，对每个棱边划分不同的单元数，得到相同载荷跨中挠度随时间变化曲线，如图2所示。综合计算所需时间和结果来看，对胞元棱边进行四等分，既可以保证足够的精度，还可以节约计算时间，下面的计算对胞元棱边均划分为四个单元。

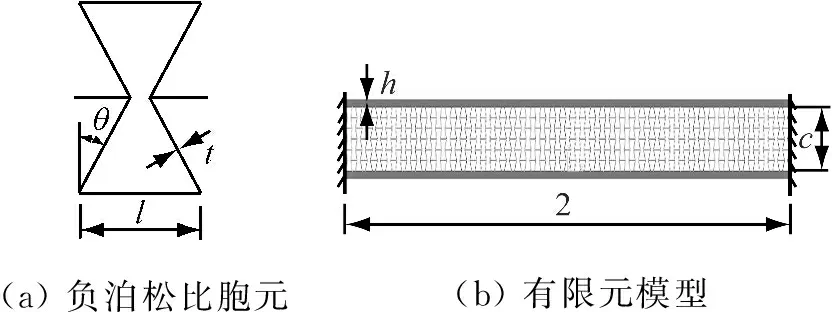
(a)负泊松比胞元(b)有限元模型

图1 梁的有限元模型

Fig.1 Schematic of sandwich beam

图2 底部面板跨中挠度随时间变化曲线

Fig.2 The relationship between the displacement of mid-span of the facet at the bottom and time

1.2 复合梁芯层的密度

负泊松比蜂窝芯层的相对密度可以表示为

(1)

式中：ρ*为负泊松比蜂窝的密度；c为芯层的厚度；li为胞壁长度，均为3 mm。

2 数值计算结果

2.1 加载方式

炸药在空气中或水中爆炸产生的冲击波的强度随指数衰减[22]，假设在t=0时刻冲击波作用到三明治梁面层上，其压力为P=P0e(-t/t0)，其中P0为峰值压力，t0为衰减时间(量级为0.1 ms)，在整个时间历程对爆炸载荷P积分得到单位面积的冲量为I

(2)

由于爆炸产生的冲击波的峰值压力P0远大于复合梁的准静态失效载荷Pc。Norman[23]认为当η=P0/Pc>10时，作用在梁上具有有限冲量的压力载荷可视为脉冲载荷，而对其挠度的影响可以忽略。

对于典型的三明治复合梁，胞元扩张角为15°，拉胀芯层的厚度c=17.4 mm，胞元壁厚t15=0.094 mm，相对密度0.051 6，复合梁面密度为38.96 kg/m2。考察均匀分布在三明治梁面层上有限压力p(t)对梁跨中挠度的影响。压力表达式为

(3)

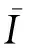
(4)

从图3上可以看出，对于η≥10，均匀分布的压力载荷与脉冲载荷的结果非常接近。基于实用的目的，三明治梁在空气或水中的冲击载荷可以近似的视为脉冲载荷[24]，在下面的计算中也采用同样的方法。

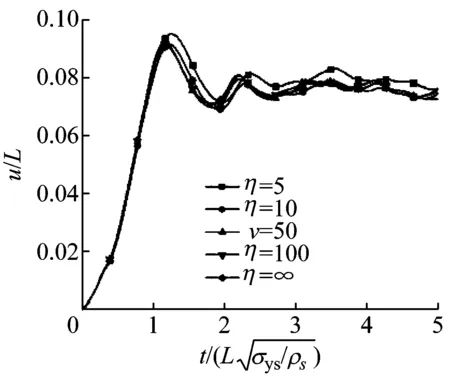
图3 三明治梁的跨中挠度

2.2 拉胀三明治梁的抗爆特性

拉胀三明治梁由拉胀芯层和两块面板组成作用在复合梁上的无量纲化冲量为0.008，图4给出了不同时刻的梁的变形。

(a) 0.05 ms

(b) 0.20 ms

(c) 0.50 ms

由于爆炸载荷的峰值压力比较高，载荷作用的时间τ远小于结构响应的时间，爆炸产生的脉冲传递到面板上，前面板获得一个初速度v0，在两端形成向中间移动的塑性铰，如图4(a)所示。在前面层塑性铰中间的部分，几乎以恒定的速度压缩芯层，如图4(b)所示。图4(c)揭示了前面板和芯层的变形，从而导致背部面板的挠度进一步增大。

图5给出了拉胀三明治梁和实体梁跨中位移随时间的变化关系，相同面密度下实体梁的等效厚度为4.897 mm。复合梁背部面板的跨中最大位移为15.90 mm，实体梁为18.20 mm。从响应时间上看，三明治梁背部面板达到最大位移时的时间比实体梁延迟约0.12 ms。可见，在冲击过程中由于拉胀芯层被压溃，不仅可以明显降低复合梁的跨中最大位移，还能延迟背板达到最大位移的时间。在吸收能量方面，如图6所示，复合梁中芯层和前面板耗散了了大部分的能量，背部面板吸收的能量仅占12%，复合梁吸收的总能量约为实体梁的2.8倍。

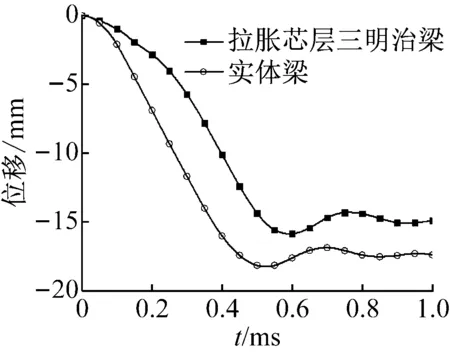
图5 背部面板跨中位移比较

图6 塑性耗散能量比较

3 参数设计与讨论

3.1 面层厚度的影响

如前所述，复合梁中的面层尤其是前面层，不仅自身可以耗散能量，还可以保护芯层，将爆炸载荷分散至整个梁上，使复合梁吸收更多的能量。改变前面层的厚度，复合梁的刚度和面密度都会有相应的提高，为了得到面层厚度对复合梁抗暴性能的影响，寻求复合梁的最佳尺寸，通过改变面层的厚度，考察复合梁的能量吸收能力和背部面板的挠度。芯层的壁厚为0.05 mm，其他计算参数如表1所示。无特殊说明，文中无量纲化脉冲均为8.0×10-2。

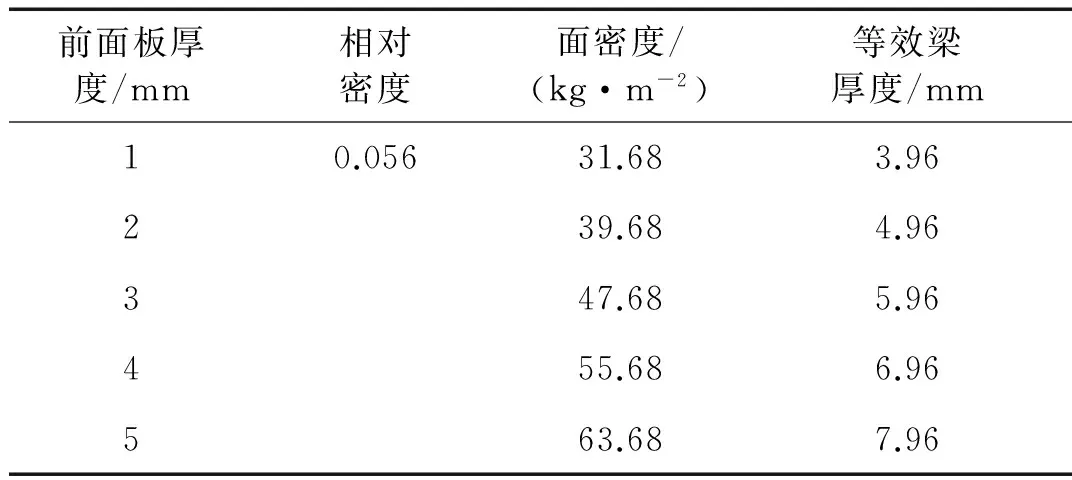
表1 不同厚度前面板的数值计算参数

如图7所示，随着复合梁前面板厚度的增大，复合梁的抗弯刚度增大，背部面板跨中挠度与实体钢梁的挠度差距变小。前面板厚度为5 mm时，背部面板最大位移和实体梁的挠度相当。从吸收能量的角度来看，前面板厚度增加，复合梁的塑性变形降低，芯层吸收的能量减少，面板厚度超过3.5 mm时，前面板吸收的能量超过芯层，前面层厚度增加，复合梁吸收的能量趋向于实体梁。

(a) 背部最大位移

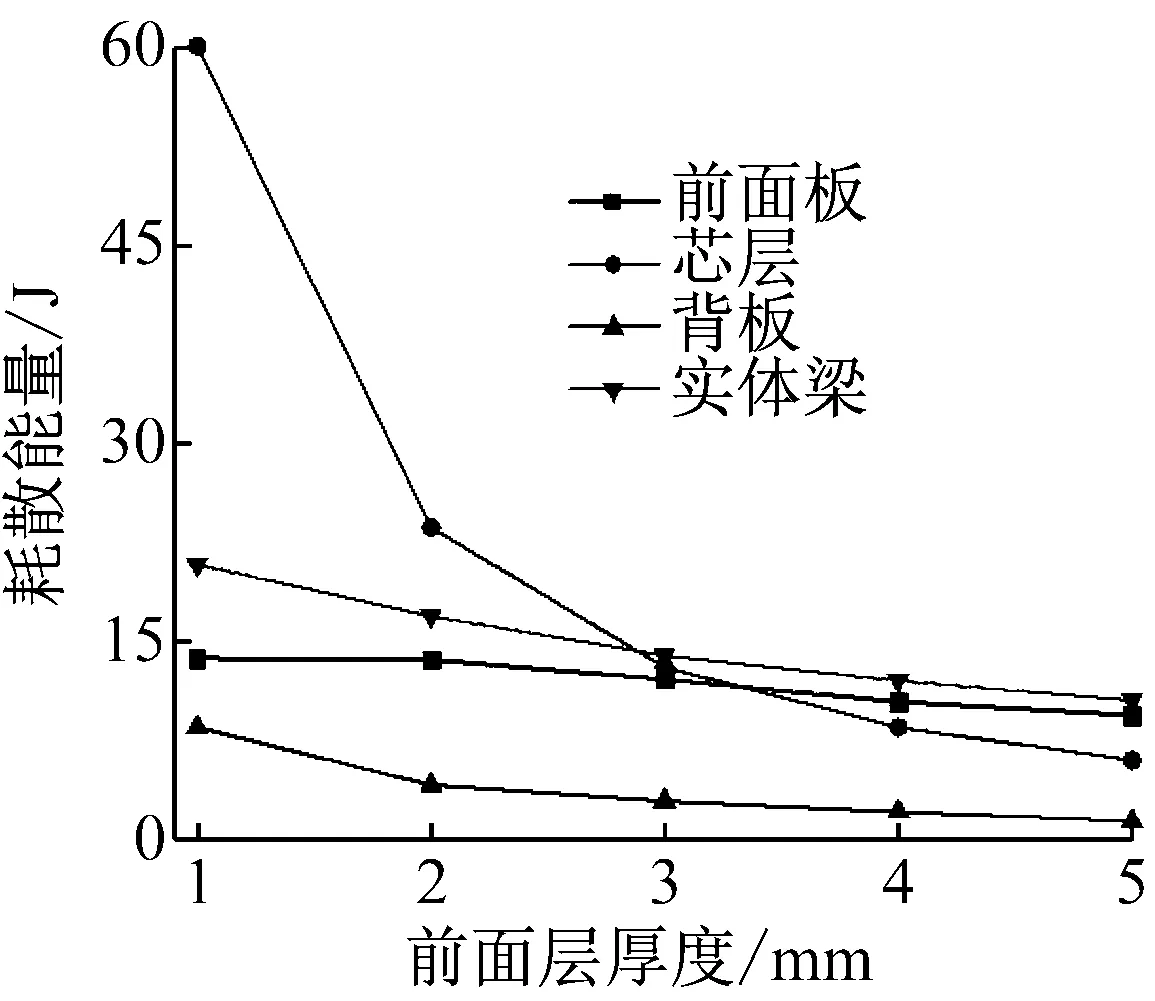
(b) 能量吸收

Fig.7 Comparison of maximum back facet displacements and plastic dissipation energies, for the auxetic sandwich beam and an equivalent beam

3.2 胞元壁厚的影响

在强冲击载荷作用下，拉胀芯层胞元的壁厚会直接影响复合梁背部面板的挠度、能量吸收效率等抗爆特性。前后面层的厚度仍为2 mm，改变胞元壁厚，在相同面密度条件下实体钢梁的厚度也将发生变化，具体参数如表2所示。

图8给出了在相同载荷下，芯层胞元壁厚变化对背部面板挠度的影响。在给定的载荷作用下，拉胀芯层胞壁的厚度小于0.12 mm时，拉胀芯层的背部面板跨中的挠度低于相应的实体钢梁。当壁厚超过0.12 mm，复合梁背板的跨中挠度比实体钢梁大，原因可能在于增大胞元壁厚，复合梁抗弯刚度变化不大，而实体梁的厚度由4.48 mm增至7.84 mm，抗弯刚度为起初的5.36倍，从而导致跨中最大挠度降低。从图8(b)上可以看出，随着拉胀芯层胞壁厚度增加，与相应的实体梁相比，复合梁吸收了更多的能量。复合梁耗散的能量仍然主要由芯层和前面板来承担，但随芯层壁厚的增加，面板吸收的能量的比重降低，而背部面板吸收的能量受芯层壁厚的影响并不大。

表2 不同壁厚的数值计算参数

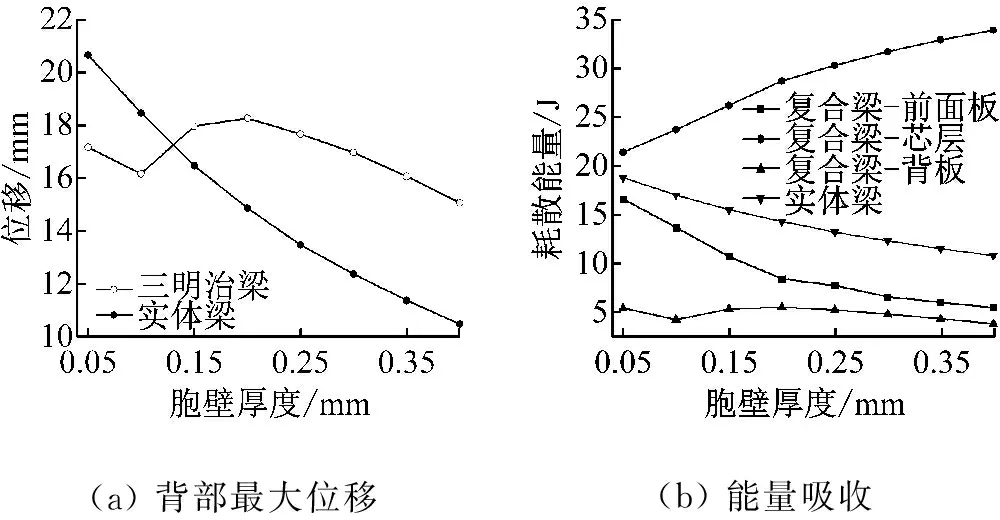
(a)背部最大位移(b)能量吸收

图8 背部最大位移和能量吸收比较

Fig.8 Comparisons of maximum back facet displacements and plastic dissipation energies, for the auxetic sandwich beam and an equivalent beam

3.3 胞元扩张角的影响

改变胞元扩张角θ，可以得到不同的拉胀胞元，其力学性能和几何参数也随之变化。本文中讨论的复合梁面层厚度不变，芯层采用三种具有代表性的胞元，相应的胞元扩张角为5°，15°，25°。拉胀芯层由于角度的变化，芯层的高度会随胞元扩张角的增大而减小。为了获得相同的面密度，不同扩张角的胞元的壁厚不同，具体参数如表3所示。

表3 三种胞元的设计参数

所有的面板承受相同的载荷，背部跨中位置的速度及位移随时间变化曲线如图9所示。从图9(a)上可以看出，扩张角不同的三种复合梁和实体梁的最大速度差别很小，但达到最大速度所需的时间存在明显差异，三种芯层的拉胀三明治梁(θ=5°,15°,25°)背部跨中达到最大速度所需的时间分别为0.43 ms，0.35 ms和0.25 ms，实体梁达到最大速度的时间仅为0.13 ms。从复合梁和实体梁的背部跨中位移来看，三种三明治梁的背部跨中最大位移依次为15.84 mm、15.85 mm和17.10 mm，实体梁的背部最大位移为18.30 mm。图10为拉胀复合梁与实体梁的耗能时间曲线，对于三明治梁，芯层胞元扩张角为25°时，芯层吸收的能量最多，而其他两种扩张角的三明治梁，由于芯层壁厚的差别比较小，吸收的能量几乎没有差别。

(a)背部面板跨中速度(b)最大位移

图9 相同载荷下复合梁和钢梁的比较

Fig.9 Comparisons of Composite beams and equivalent monolithic beam velocities of back facet center,maximum displacement

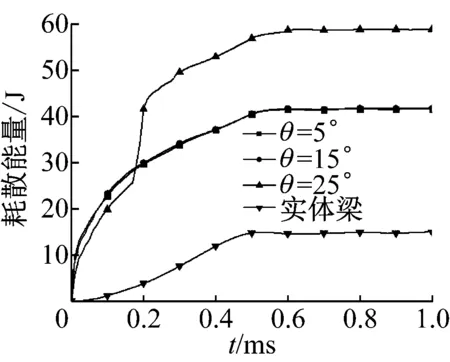
图10 耗散能量曲线

图11为复合梁跨中名义应变的时间历程曲线，其名义应变定义为

(5)

式中：ub为背部面板的位移，uf为前面板的位移。从图11上可以看出，三种芯层跨中最大名义应变约为0.8，均已达到密实状态。胞元扩张角为25°的三明治梁芯层达到密实状态的时间为0.20 ms，而其他两种三明治梁芯层达到密实状态的推迟至0.30 ms。可能的原因在于，芯层胞元扩张角为25°时，胞壁的厚度最小，芯层的刚度低，冲击过程中被压溃的胞元比例大，从而吸收了更多的能量。可见，采用不同芯层的复合梁，会改变其背部面板的位移，但与实体梁相比，从背板的最大位移和吸收能量方面来看，仍具有明显的优势。

图11 跨中芯层名义应变时间曲线

3.4 冲击载荷强度的影响

复合梁的动态力学响应不仅和自身的几何尺寸有关，还严重依赖于冲击载荷的强度。仍以胞元扩张角为15°、相对密度为0.05的复合梁与同面密度的实体梁为例。图12(a)给出了在不同载荷作用下拉胀复合梁背板和实体梁的最大位移随冲击载荷强度的变化关系式。对于实体梁，最大位移随载荷强度几乎成线性，而复合梁则具有明显的非线性。就背部最大位移而言，当无量纲脉冲载荷强度低于0.085时，实体梁的最大位移比复合梁小，当梁受到的载荷比较大时前面层得到较大的初速度，迅速压溃芯层，吸收了大量的能量，传递到背部面板上的能量低，从而导致背部面板的最大位移低于实体梁。图12(b)比较了复合梁各组成部分以及实体梁通过塑性变形的耗能情况。实体梁吸收的能量约为复合梁的35%。对复合梁而言，各部分耗散的能量均随载荷的增大而增多，但在吸收的总能量中的比例基本没有变化。

(a)背部最大位移(b)能量吸收

图12 背部最大位移和能量吸收比较

Fig.12 Comparison of maximum back facet displacements and plastic dissipation energies, for the auxetic sandwich beam and an equivalent beam

4 结 论

运用数值方法对两端固支的拉胀复合梁在强冲击载荷作用下的动态响应和能量吸收能力进行了讨论，三明治梁由多层典型的拉胀胞元和面层组成，并和同面密度的实体梁进行了对比。通过对以上内容的研究可得出如下结论：

(1) 前面板厚度增大，芯层吸收的能量降低，背部面板的最大位移及复合梁吸收的能量趋向于相应的实体梁。

(2)在相同面密度的情况下，变化胞元扩张角，背板的最大位移变化并不大，但胞元扩张角大，胞壁厚度小，吸收的能量多。

(3)对于文中给定的复合梁及相应的实体梁，其跨中最大位移取决于载荷的强度。无量纲脉冲载荷强度低于0.085时，实体梁的最大位移比复合梁小；无量纲脉冲强度超过0.085时，芯层胞元压溃数目增大，耗散的能量多，与实体梁相比，复合梁的跨中最大挠度小。

(4)从吸收能量的角度来看，拉胀三明治梁优于实体梁。

[1] EVANS K, ALDERSON A. Auxetic materials: functional materials and structures from lateral thinking[J]. Advanced Materials, 2000, 12(9): 617-628.

[2] 杨智春, 邓庆田. 负泊松比材料与结构的力学性能研究及应用[J]. 力学进展, 2011, 41(3): 335-350.

YANG Zhichun, DENG Qingtian. Mechanical property and application of materials and structures with negative poisson’s ratio[J]. Advances Mechanics, 2011, 41(3): 335-350.

[3] LAKES R, ELMS K. Indentability of conventional and negative Poisson’s ratio foams[J]. Journal of Composite Materials, 1993, 27(12): 1193-1202.

[4] BEZAZI A, SCARPA F. Tensile fatigue of conventional and negative Poission’s ratio open cell PU foams[J]. International Journal of Fatigue, 2009, 31: 488-494.

[5] 张新春, 刘颖,李娜. 具有负泊松比效应蜂窝材料的面内冲击动力学性能[J]. 爆炸与冲击, 2012, 32(5): 475-482.

ZHANG Xinchun, LIU Ying, LI Na. In-plane dynamic crushing of honeycombs with negative Poisson’s ratio effects[J]. Explosion and Shock Waves, 2012, 32(5): 475-482.

[6] QIU X, DESHPANDE V S, FLECK N A. Impulisive loading of clamped monolithic and sandwich beams over a central patch[J]. Journal of the Mechanics and Physics of Solids, 2005, 53: 1015-1046.

[7] XUE Z, HUTCHINSON J W. Preliminary assessment of sandwich plates subject to blast loads[J]. International Journal of Mechanical Sciences, 2003, 45(4): 687-705.

[8] YU Jinlin, WANG Erheng, LI Jianrong, et al. Static and low-velocity impact behavior of sandwich beams with closed-cell aluminum-foam core in three-point bending[J]. International Journal of Impact Engineering, 2008, 35: 885-894.

[9] RADFORD D D, FLECK N A, DESHPANDE V S. The response of clamped sandwich beams subjected to shock loading[J]. International Journal of Impact Engineering, 2006, 32: 968-987.

[10] QIAO Pizhong, YANG Mijia. Impact analysis of fiber reinforced polymer honeycomb composite sandwich beams[J]. Composites Part B Engineering, 2007，38(5/6): 739-750.

[11] RUSSELL B P, LIU T, FLECK N A, et al. The soft impact of composite sandwich beams with a square-honeycomb core[J]. International Journal of Impact Engineering, 2012, 48: 65-81.

[12] ST-PIERRE L, DESHPANDE V S, FLECK N A. The low velocity impact response of sandwich beams with a corrugated core or a Y-frame core[J]. International Journal of Mechanical Sciences, 2015, 91: 71-80.

[13] XU Guodong, YANG Fan, ZENG Tao, et al. Bending behavior of graded corrugated truss core composite sandwich beams[J]. Composite Structures, 2016, 138: 342-351.

[14] HINE P J, DUCKETT R A, WARD I M. Negative Poisson’s ratios in angle-ply laminates[J]. Journal of Materials Science Letters, 1997, 16: 541-544.

[15] JAYANTY S, CROWE J, BERHAN L. Auxetic fibre networks and their composites[J]. Physica Status Solidi B, 2011, 248(1): 73-81.

[16] HARKATI E H, BEZAZI A, SCARPA F, et al. Modelling the influence of the orientation and fiber reinforcement on the negative Poisson’s ration in composite laminates[J]. Physica Status Solidi B, 2007, 244(3): 883-892.

[17] 卢子兴,李康. 四边手性蜂窝动态压溃行为的数值模拟[J]. 爆炸与冲击, 2014, 34(2): 181-187.

LU Zixing, LI Kang. Numerical simulation on dynamic crushing behaviors of tetrachiral honeycombs[J]. Explosion and Shock Waves, 2014, 34(2): 181-187.

[18] MA Z D, BIAN H, SUN C, et al. Functionally graded NPR (negative Poisson’s ratio) material for a blast-protective deflector[C]//NDIA ground vehicle systems engineering and technology symposium. Dearborn: [s.n.], 2010.

[19] SCHENK M, GUEST S, MCSHANE G. Novel stacked folded cores for blast-resistant sandwich beams[J]. International Journal of Solid and Structures, 2014, 51(25):4196-4214.

[20] IMBALZANO G, TRAN P, NGO T D, et al. A numerical study of auxetic composite panels under blast loadings[J]. Composite Structures, 2016, 135: 339-352.

[21] RUAN D, LU G, WANG B, et al. In-plane dynamic crushing of honeycombs-a finite element study[J]. International Journal of Impact Engineering, 2003, 28(2): 161-182.

[22] SWISDAK M M. Explosion effects and properties: Part II-explosion effects in water[R]. Naval Surface Weapons Center. Dahlgren:[s.n.].

[23] NORMAN J. Structural impact[M]. Cambridge: Cambridge University Press, 1989.

[24] FLECK N A, DESHPANDE V S. The resistance of clamped sandwich beams to shock loading[J]. Journal of Applied Mechanics, 2004, 71: 386-401.

Dynamic analysis of auxetic sandwich beams under blast loading

CUI Shitang1, NI Xiaojun2, ZHANG Ke1

(1. CAS Key Laboratory of Mechanical Behavior and Design of Materials, University of Science and Technology of China, Hefei 230026, China; 2. Institute of Plasma Physics, Chinese Academy of Science, Hefei 230031, China)

The numerical method was employed to investigate the dynamic response and the ability of energy absorption of a sandwich beam with auxetic cellular cores under blast loading. Pressure time histories replacing blast loading were applied uniformly on the front facet of the sandwich beam. The back facet’ maximum displacement and energy-dissipating of the sandwich beam were compared with those of the corresponding monolithic one in the premise of the same surface load density. The facets and cores of the sandwich beam were designed parametrically with design parameters of cell thickness, thickness of front panel and expanding angle of cell elements. Under blast loading, it was shown that compared with the corresponding monolithic beam, the sandwich beam can reduce its back facet’s maximum displacement, delay the time of back facet’s reaching the maximum velocity and absorb more energy via plastic deformation of auxetic cores.

auxetic; negative Poisson’s ratio; sandwich beam; finite-element (FE) simulation

安徽省自然科学基金资助项目(1408085ME84)

2016-02-23 修改稿收到日期：2016-05-01

崔世堂 男，博士，副研究员，1978年生

张科 男，博士，1986年生

TH113

A

10.13465/j.cnki.jvs.2017.13.027