带弹性支撑的颗粒碰撞阻尼的减振机理研究

杜妍辰， 张 虹

(上海理工大学 医疗器械与食品学院， 上海 200093)

带弹性支撑的颗粒碰撞阻尼的减振机理研究

杜妍辰， 张 虹

(上海理工大学 医疗器械与食品学院， 上海 200093)

具有双重减振结构的带弹性支撑的颗粒碰撞阻尼具有优秀的减振性能。为了探索带弹性支撑的颗粒碰撞阻尼的减振机理，建立了带弹性支撑的颗粒碰撞阻尼系统的动力学模型，在Matlab环境下编制了仿真计算程序，模拟计算了在带弹性支撑的颗粒碰撞阻尼作用下的悬臂梁的减振性能。理论计算结果与实验结果进行比较，验证了提出的动力学模型。运用该动力学模型讨论了阻尼器腔体间隙比、冲击器质量比、刚度比的基本规律。得到了以下结论：① 带弹性支撑的颗粒碰撞阻尼系统的动力学模型是可靠的；② 带弹性支撑的颗粒碰撞阻尼具有优秀的减振性能，远远超过单体碰撞阻尼；③ 带弹性支撑的颗粒碰撞阻尼最优的结构参数组合(间隙比为0.15，刚度比为0.007)。

碰撞阻尼； 颗粒； 弹性支撑； 动力学模型

碰撞阻尼属于振动的被动控制技术，它利用振动过程中自由质量(冲击器)与主系统的碰撞来控制主系统的响应。碰撞阻尼器构造简单、成本低廉、易于实施、无需外电源、适合在恶劣环境下使用并且减振效果良好。关于碰撞阻尼的研究在最近得到了迅猛的发展，目前有代表性的碰撞阻尼包括：单体碰撞阻尼[1-2]、豆包碰撞阻尼[3-4]、多体碰撞阻尼[5]、颗粒碰撞阻尼[6-12]、非阻塞性颗粒碰撞阻尼(Non-Obstructive Particle Damping)[13-14]、带颗粒减振剂的碰撞阻尼[15-20]等。

很多文献都指出，在碰撞耗能过程中，碰撞恢复系数是个重要的参数，碰撞恢复系数的变化直接影响了碰撞阻尼减振的效果。但对于二者是正相关还是负相关，却存在着不同的看法。Dokainish等[21-22]的研究认为随着碰撞恢复系数增大，碰撞减振的等效阻尼也增大；Pinotti等[23]的研究却认为随着碰撞恢复系数增大，碰撞减振的等效阻尼在减小，这导致了碰撞阻尼的两种完全不同的发展方向：① 利用接近弹性的碰撞，尽可能增大碰撞恢复系数，典型的例子是Li等[24]设计了带缓冲的弹性碰撞阻尼器，有效地降低了碰撞过程中的加速度，同时也取得了更好的减振效果；② 利用接近塑性的碰撞，尽可能减小碰撞恢复系数，典型的例子是带颗粒减振剂的碰撞阻尼[25]，实验结果表明，带颗粒减振剂的碰撞阻尼器在低频振动(<50 Hz)中具有优秀的减振效果，在共振频率点处可使悬臂梁的末端最大振幅下降幅度超过65%，远远超过单体碰撞阻尼器和颗粒阻尼器。

本文提出一种具有双重减振结构的碰撞阻尼，称为带弹性支承的颗粒碰撞阻尼，结构见图1。它采用在塑性碰撞阻尼器的基础上增加弹性支承的方法实现两级减振：外层的弹性支撑采用具有较大恢复系数的弹簧，使得阻尼器与主系统之间产生充分的动量交换，同时弹簧的放大作用使得阻尼器能够充分吸收主系统的动能；内层的塑性碰撞阻尼器具有较小的恢复系数，可充分消耗阻尼器通过动量交换而吸收的动能，使其不再返回主系统。其优点很明显：结构上采用内外分离的两层减振形式，外层用弹簧实现了较大的恢复系数，内层用塑性碰撞阻尼器实现较小的恢复系数；原理上外层实现动量交换，使得碰撞主要以对碰的形式产生，以充分降低主结构的振幅，内层实现充分耗能，使得附加质量上的动能不再返回主系统。两层结构可以使得两种减振机理的特点都能充分发挥出来，减振效果达到最大化，这是传统的碰撞阻尼器无法实现的。对悬臂梁减振实验如图2所示，带弹性支撑的颗粒碰撞阻尼具有优秀的减振性能，可使悬臂梁自由端的最大振幅下降80%，远远超过单体碰撞阻尼。

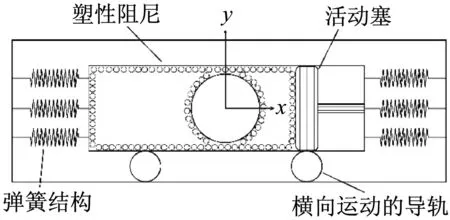
图1 带弹性支承的颗粒碰撞阻尼器结构示意图

图2 悬臂梁自由端在共振点区域的最大振幅

带弹性支承的颗粒碰撞阻尼器不是简单的弹性碰撞阻尼器和塑性碰撞阻尼器的组合，弹簧的放大作用不仅使阻尼器能与主系统交换更多的动量，还可以使得塑性碰撞阻尼器中的撞击更猛烈，耗能也更多；同时两层减振结构将会带来丰富的动力学特性，在学术上也非常值得进行深入研究。为此本文首先根据带弹性支承的颗粒碰撞阻尼器的结构特点，建立了带有两层减振结构的动力学模型。通过实验检验所建模型的正确性，最后运用该动力学模型，分析阻尼器腔体间隙比、冲击器质量比、刚度比的基本规律。

1 带弹性支撑的颗粒碰撞阻尼器的动力学建模

1.1 建立系统微分方程

本文建立了一个两自由度的模型表示带弹性支撑的颗粒碰撞阻尼器的振动模型，如图3所示。该系统由三个质量体m1、m2、m3，两个刚度k1、k2和两个阻尼c1、c2构成。主质量m1在外部正弦激振力F(t)的作用下将产生振动。

为方便计算，采取下面几个假设：

(1) 在此过程中，相对于摩擦耗能来说，碰撞耗能占主导地位。首先是碰撞间隙很小，所以忽略m3和m2之间的摩擦力；其次由于导轨设计合理且滑道间有润滑，因此m2和m1之间的摩擦也予以忽略。

(2) 该碰撞是非弹性碰撞，碰撞前后的关系用恢复系数e进行模拟。

(3) 只考虑水平方向的振动。

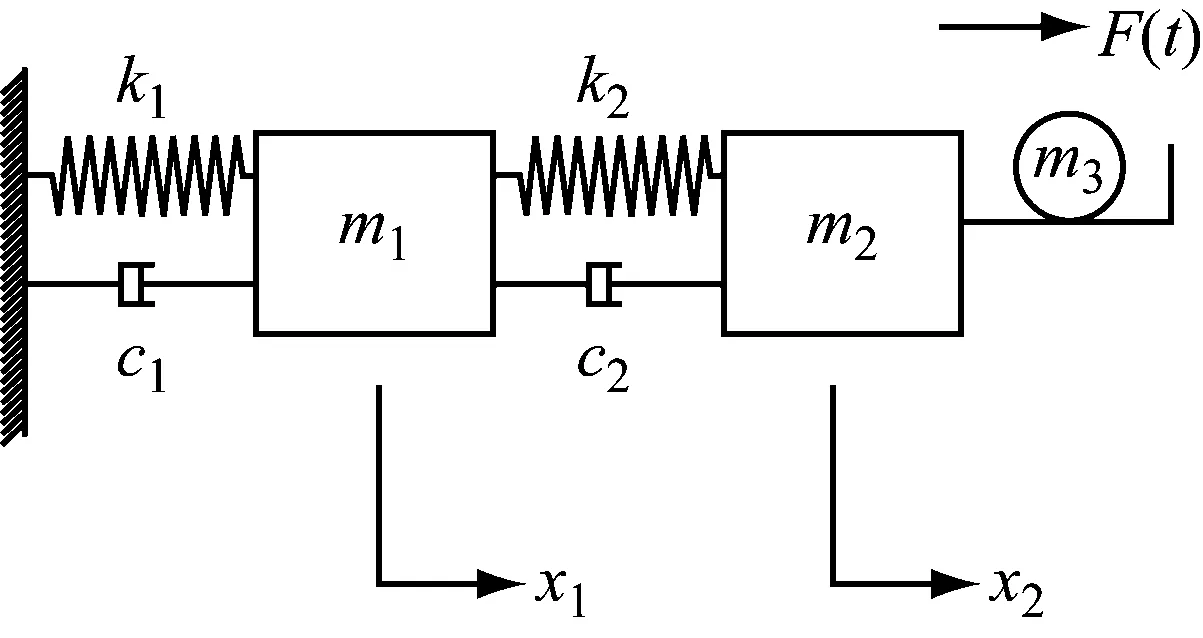
图3 带弹性支承的颗粒碰撞阻尼器的动力学模型

m3对m2的碰撞每周期消耗一定值的能量，为了便于分析，我们用能量法来将其简化成等效阻尼的方式，使得其一周期内消耗的能量等于球和腔体碰撞产生的能量。此等效阻尼作用于腔体即m2，可通过能量法来近似估算该等效阻尼大小。

(1)

因此系统的运动微分方程可表示为

(2)

系统的动能为

(3)

系统的势能为

(4)

系统的能量耗散函数为

(5)

1.2 模态分析

首先对该系统的无阻尼系统作振动分析，以求得一阶和二阶的固有频率及对应的主振型。

设主振动为

x=φ(sinωt+φ)

(6)

式中，φ=[φ1,φ2]为特征向量，在振动中，称φi为第i阶主振型。系统的特征方程为

|K-λ2M|=0

(7)

通过式(7)解出系统的2个特征值λ1、λ2，特征值取决于系统的刚度质量等参数。2个特征值的平方根依次称为系统的第i阶固有频率，各个坐标都以第i阶固有频率来振动称为第i阶主振动。2个主振动叠加为系统的固有振动。

1.2.1 求该2自由度系统的模态矩阵

(K-λ2M)是系统的特征矩阵，标记为B，可通过将特征值带入B的伴随矩阵adj(B)来求得对应的主振型φi。主振型具有正交性，当主振型的固有频率不同时，质量矩阵和刚度矩阵都与其正交。

当固有频率相同的主振型之间，则有

φi=Mpi

(8)

(9)

式中：Mpi为第i阶主质量;Kpi为第i阶主刚度。

计算该系统的动力矩阵

H=M-1K

(10)

将式(10)代入式(11)

|λI-H|=0

(11)

解出特征值λ，然后令[λI-H]=[f(λ)]，求得[f(λ)]的伴随矩阵[F(λ)]。

将λ值带入伴随矩阵[F(λ)]，重组成[F(λr)]。对应3个特征值，均选取[F(λr)]一个非零列，然后组成一个新的矩阵。就是我们要求的模态矩阵。

1.2.2 坐标变换

利用它的振型矩阵Φ和谱矩阵来进行坐标变换，已经求得的振型矩阵或是模态矩阵表示为

Φ=[φ1,φ2]

(12)

对系统坐标进行如下的变换

x=Φη

(13)

则原来的振动方程变为

(14)

即

(15)

式中，Q(t)为主坐标下的激振力，表示为

(16)

其中,

ΦTMΦ=Mp

(17)

ΦTKΦ=Kp

(18)

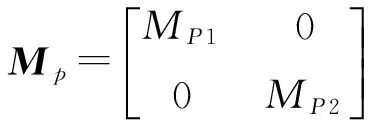
同样地，将阻尼矩阵变换得

ΦTCΦ=Cp

(19)

变换后的Cp不是对角阵，因此系统中耦合仍然存在。为了仍能使用主坐标法来进行计算，本文中采用将Cp的非对角元素忽略的方式，使得Cp成为下面的对角阵

(20)

式中，Cpi为第i阶主振型的阻尼系数。

1.3 稳态响应

如此，式(15)得到解耦，其中第i个方程为

(21)

或写为

(22)

式中，ξi为第i阶振型阻尼比。易得该主振型的稳态响应

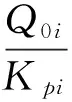
(23)

式中：φi为第i阶相位差；βi为第i阶的放大因子。定义如下

(24)

(25)

式中，λi为激励频率与系统第i阶固有频率之比，称为第i阶频率比，表达为

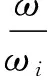
(26)

系统方程可以表示为

(27)

将式(27)进行拉普拉斯变换并认为初始条件是0

(s2M+sC+K)x(s)=F(s)

(28)

式中：x(s)和F(s)为对应的拉普拉斯变换；s为复变量。令

G(s)=(s2M+sC+K)-1

(29)

把它叫做传递函数矩阵，那么

x(s)=G(s)F(s)

(30)

将G(s)变形可以得到其模态展开式

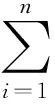
(31)

将式(31)做s=iω变换，得到的是复频响应函数矩阵H(ω)，所以式(30)可写为

x(ω)=H(ω)F(ω)

(32)

式中，x(ω)和F(ω)分别为稳态响应和激振力向量的傅里叶变换，所以H(ω)的模态展开式为

(33)

代入式(24)和式(25)得

(34)

将该振动系统的稳态响应表示为如下的复数形式

(35)

同样的，也将式(2)中的Fsinωt变为复数形式Feiωt，再将式(34)代入，便可以得出

(36)

由式(34)及式(36)得到

(37)

本系统是2自由度，所以n=2，所以得到系统的稳态响应表示为

φi)

(38)

1.4 参数计算

1.4.1 质量和刚度

主系统质量m1为1.531 kg，阻尼器质量m2为0.359 kg，冲击小球质量m3为0.024 kg。

悬臂梁的截面惯性矩：I=bh3/12=153.6 mm4

悬臂梁的刚度：k1=3EI/l3=7.8 N/mm

1.4.2 阻尼

由阻尼器产生的阻尼比容为

(39)

式中：ΔT为一个循环中动能转化为热能的大小；T为一个循环中的最大动能。

ΔT可表示如下

(40)

循环中最大动能在主系统速度达到最大时其动能最大，由于m1质量相对较大，因此系统的最大动能可近似于m1的最大动能，计算如下

(41)

作用于m2上的碰撞近似为阻尼

(42)

1.5 计算流程

本文利用Matlab将以上解答流程编程。Matlab编写计算程序的流程图如图4所示。

图4 Matlab仿真程序流程图

2 模型计算结果与实验结果的比较

取阻尼器腔体间隙为36 mm，填充颗粒为铜粉，填充率为20%。悬臂梁刚度为7.8 N/mm，单个弹簧的刚度为0.34 N/mm，则对应的腔体两端弹簧数量分别为8组，6组，4组，2组时的弹簧刚度分别为：1.36 N/mm，1.02 N/mm，0.68 N/mm，0.34 N/mm。模型计算结果与实验结果的比较如图5所示，Matlab模拟的结果与实验结果有着较好的一致性，验证了所建立的系统动力学模型是正确的。

(a) 2组弹簧

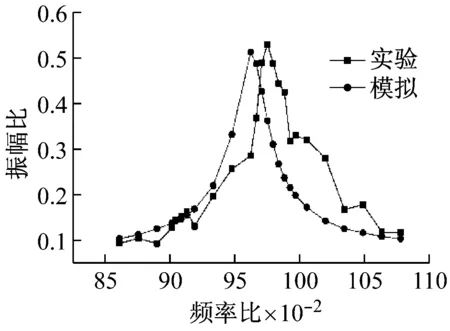
(b) 4组弹簧

(c) 6组弹簧

(d) 8组弹簧

3 模型计算结果分析(参数优化)

运用建立的动力学模型对带弹性支承的颗粒碰撞阻尼器进行数值模拟，探索各结构参数对阻尼器减振效果影响的基本规律，找出优化参数。

首先定义几个无量纲值：① 振幅比，系统稳态振幅/无附加阻尼振幅；② 间隙比，间隙/无附加阻尼振幅；③ 频率比，激振频率/无阻尼自振频率；④ 刚度比，附加弹簧刚度/主梁刚度；⑤ 冲击质量比，小球质量/阻尼器质量；⑥ 功率比，输入功率/系统额定功率；⑦ 振幅衰减率。

振幅衰减率

σ=(AR-XR)/AR×100%

(43)

式中：AR为主系统在无阻尼时的最大振幅；XR为主系统在带弹性支撑的颗粒碰撞阻尼器作用下的最大振幅。

3.1 间隙比的影响

计算不同刚度值条件下间隙比(见表1)对系统振幅比的影响(见图6)，以确定系统的最佳腔体间隙值。

由图6可以看出：① 存在最佳的间隙比1.5；② 随着间隙比的增加，系统的振幅比呈现先减小后增大的趋势。

3.2 冲击器质量比的影响

阻尼器腔体直径为20 mm，冲击质量比见表2。取间隙比1.5，刚度比0.174，计算得到的冲击器质量比的影响如图7所示。

表1 间隙比

图6 间隙比对振幅比的影响

表2 冲击质量比

图7 冲击质量比对振幅比的影响

由图7可以看出，随着冲击质量比的增大，即冲击质量的增加，振幅比逐渐下降，当冲击质量比增至0.067附近时，振幅比大约降至0.57，之后下降趋于平缓，继续增大冲击质量比，振幅比变化不大。

3.3 刚度比的影响

取表3所示的一组13个不同的刚度比，计算得到不同的刚度比对应的系统振幅比如图8所示。间隙比1.5，冲击器质量比0.067。

表3 刚度比

图8 共振点处振幅比与刚度比的关系

由图8可以看出：① 存在最佳刚度比，最佳刚度比0.007；② 随着刚度比的增大，即附加刚度值的增加，系统的振幅缓慢增加，在刚度比为0.044以下时表现良好，但是刚度值大于0.044后会快速上升；③ 刚度比小于0.044时系统的振幅先减小后增大，但增幅不大。

4 结 论

本文通过对带弹性支撑的颗粒碰撞阻尼减振机理的理论建模和实验研究，得到以下结论：

(1) 本文建立的带弹性支撑的颗粒碰撞阻尼系统的动力学模型是可靠的。

(2) 带弹性支撑的颗粒碰撞阻尼具有优秀的减振性能，振幅衰减率可达80%。

(3) 带弹性支撑的颗粒碰撞阻尼存在最优的参数组合(间隙比为0.15，刚度比为0.007)。

[1] CHENG C C, WANG J Y. Free vibration analysis of a resilient impact damper[J]. International Journal of Mechanical Sciences, 2003,45(4):589-604.

[2] CHENG J, XU H. Inner mass impact damper for attenuating structure vibration[J]. International Journal of Solids and Structures, 2006,43(17):5355-5369.

[3] POPPLEWELL N, SEMERCIGIL S E. Performance of the bean bag impact damper for a sinusoidal external force[J]. Journal of Sound and Vibration, 1989,133(2):193-223.

[4] 李伟，胡选利，黄协清，等.柔性约束颗粒阻尼耗能特性研究[J].西安交通大学学报,1997,31(7): 23-28.

LI Wei, HU Xuanli, HUANG Xieqing, et al. Study on energy dissipation characteristics of granular damping with flexible boundary[J]. Journal of Xi’an Jiaotong University,1997,31(7): 23-28.

[5] SAEKI M. Analytical study of multi-particle damping[J]. Journal of Sound and Vibration,2005,281(3/4/5):1133-1144.

[6] WONG C X, DANIEL M C, RONGONG J A. Energy dissipation prediction of particle dampers[J]. Journal of Sound and Vibration,2009,319(1/2):91-118.

[7] SHAH B M, NUDELL J J, KAO K R,et al. Semi-active particle-based damping systems controlled by magnetic fields[J]. Journal of Sound and Vibration, 2011,330(2):182-193.

[8] 鲁正，吕西林，闫维明.颗粒阻尼技术研究综述[J].振动与冲击,2013,32(7):1-7.

LU Zheng, LÜ Xilin, YAN Weiming. A survey of particle damping technology[J]. Journal of Vibration and Shock, 2013,32(7):1-7.

[9] 马崇武，慕青松.颗粒阻尼器对悬臂梁自由振动的被动减振作用[J].兰州理工大学学报,2014,40(3): 165-168.

MA Chongwu, MU Qingsong. Passive damping effect of particle damper on free vibration of a cantilever beam[J]. Journal of Lanzhou University of Technology, 2014,40(3): 165-168.

[10] 胡溧，唐喆，徐贤，等. 颗粒阻尼器损耗因子外特性研究[J].中国机械工程,2015,26(15):2005-2009.

HU Li, TANG Zhe, XU Xian, et al. Study on external features of particle damping loss factor[J]. China Mechanical Engineering, 2015,26(15):2005-2009.

[11] TRIGUI M, FOLTETE E,BOUHADDI N. Prediction of the dynamic response of aplate treated by particle impact damper[J]. Mechanical Engineering Science, 2014,228(5): 799-814.

[12] GHARIB M, KARKOUB M. Shock-based experimental investigation of the linear particle chain impact damper[J]. Journal of Vibration and Acoustics, 2015,137(6):061012.

[13] PANOSSIAN H. Non-obstructive particle damping experience and capabilities[C]∥The International Society for Optical Engineering.[S.l.]: SPIE, 2002: 936-941.

[14] 周宏伟，陈前.阻尼颗粒动态特性研究[J].南京航空航天大学学报,2008,40(6):742-746.

ZHOU Hongwei, CHEN Qian. Experimental investigation on damping particle dynamic characters[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008,40(6):742-746.

[15] 杜妍辰，王树林.等代参数法预测颗粒夹击过程中的能量损耗[J].振动与冲击,2011,30(12):160-163.

DU Yanchen, WANG Shulin. Equivalent parameter method for predicting energy dissipation in particle clamping[J]. Journal of Vibration and Shock, 2011,30(12):160-163.

[16] 杜妍辰，张铭命.带颗粒减振剂的碰撞阻尼的理论与实验[J].航空动力学报,2012,27(4):789-794.

DU Yanchen, ZHANG Mingming. Theoretical and experimental research on impact damping with fine particles as damping agent[J]. Journal of Aerospace Power, 2012,27(4):789-794.

[17] 李海超，王树林，杜妍辰，等. 颗粒碰撞阻尼的时效性研究[J].振动与冲击,2013,32(15):156-160.

LI Haichao, WANG Shulin, DU Yanchen, et al. Durability of particle impact dampers[J]. Journal of Vibration and Shock,2013,32(15):156-160.

[18] 杜妍辰，刘喆，李海超.带弹性支承的颗粒-钢球碰撞阻尼的实验研究[J].振动与冲击,2013,32(24):56-60.

DU Yanchen, LIU Zhe, LI Haichao. Tests for a particle-ball impact damper with elastic support[J]. Journal of Vibration and Shock,2013,32(24): 56-60.

[19] 杜妍辰，葛静静.带颗粒减振剂的碰撞阻尼器实验[J].机械设计与研究,2015,31(1):51-54.

DU Yanchen, GE Jingjing. Experimental research on impact damping with the shock absorbent[J]. Machine Design and Research,2015,31(1):51-54.

[20] 杜妍辰，张虹.组合式颗粒阻尼器的减振实验研究[J].中国机械工程,2015,26(14):1953-1958.

DU Yanchen, ZHANG Hong. Experimental research on combined particle impact damper[J]. China Mechanical Engineering,2015,26(14):1953-1958.

[21] DOKAINISH M A, ELMARAGHY H. Optimum design parameters for impact dampers[C]∥The ASME Publications Design Engineering and Technical Conference. Cincinnati: ASME, 1973:1-7.

[22] POPPLEWELL N, LIAO M. A simple design procedure for optimum impact dampers[J]. Journal of Sound and Vibration, 1991,146(3):519-526.

[23] PINOTTI P C, SADEK M M. Design procedure and charts for the impact damper[C]∥Proceedings of the 11th International Machine Tool Design and Research Conference. Birmingham:[s.n.], 1970:181-195.

[24] LI K, DARBY A P. An experimental investigation into the use of a buffered impact damper[J]. Journal of Sound and Vibration,2006,291(3/4/5): 844-860.

[25] 杜妍辰, 王树林, 朱岩,等. 带颗粒减振剂碰撞阻尼的减振特性[J]. 机械工程学报,2008,44(7):186-189.

DU Yanchen, WANG Shulin, ZHU Yan,et al. Vibration characteristics of a new fine particle impact damping[J]. Journal of Mechanical Engineering, 2008,44(7): 186-189.

Damping mechanism of an elastically supported particle impact damper

DU Yanchen， ZHANG Hong

(School of Medical Instrumentation and Food Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

An elastically supported particle impact damper (ESPID) with double damping structures has excellent damping performances. Here, in order to study the damping mechanism of the damper, the dynamic model of the damper was built. A simulation procedure was programmed in Matlab, the damping performance of a cantilever beam with the damper was simulated using the program. The dynamic model was verified by comparing the results of numerical simulation with test ones. Then using the dynamic model, the laws of the damper’s chamber clearance ratio, impactor mass ratio, stiffness ratio, were discussed. The results showed that ① the dynamic model of the ESPID is reliable; ② the performance of the ESPID is much more excellent than that of a single impact damper; ③ the optimal structure parameters of the ESPID are clearance ratio of 0.15 and stiffness ratio of 0.007.

impact damper; particle; elastic support; dynamic model

国家自然科学基金资助项目(51475308)

2015-10-27 修改稿收到日期：2016-01-28

杜妍辰 女，博士，副教授，1976年生

O328; TB53

A

10.13465/j.cnki.jvs.2017.13.010