一种冲击波压力传感器的准静态校准神经网络模型

赵传荣， 孔德仁， 王胜强， 商 飞

(1.安徽工业大学 电气与信息工程学院，安徽 马鞍山 243032； 2.南京理工大学 机械工程学院，南京 210094； 3.西安近代化学研究所，西安 710065)

一种冲击波压力传感器的准静态校准神经网络模型

赵传荣1， 孔德仁2， 王胜强3， 商 飞2

(1.安徽工业大学 电气与信息工程学院，安徽 马鞍山 243032； 2.南京理工大学 机械工程学院，南京 210094； 3.西安近代化学研究所，西安 710065)

由冲击波压力传感器准静态校准原理，间接比对式校准的精度取决于重锤的落高与压力拟合模型的精度，本文采用RBF神经网络建立了以落高为输入量、冲击波压力峰值为输出量的神经网络模型。选用典型标准压力传感器，在7～30 MPa量程范围开展校准实验；通过对测试样本进行分析，结果表明：该神经网络模型预测的最大相对误差不超过0.04%，比多项式拟合模型和指数拟合模型高一个数量级。落高与压力拟合模型引入的不确定度是构成冲击波压力传感器动态测量不确定度的一个重要分量，通过建立高精度的重锤落高与冲击波压力峰值神经网络拟合模型，为进一步提高冲击波压力传感器的测量精度奠定了基础。

冲击波压力传感器；RBF神经网络；准静态校准；拟合模型

冲击波压力的大小是评价武器威力的一个重要指标，为定量地评定各类武器或爆炸器材的威力及计算爆炸释放能量与燃烧率，准确测量冲击波压力具有十分重要的意义。

目前常用的压电式冲击波压力测量传感器，无论是ICP(Integrated Circuit Piezoelectric)型还是高阻抗输出型，在实际使用中存在以下几个问题：

(1) ICP型和压电式高阻输出的冲击波压力传感器的灵敏度一般都是依靠生产厂家提供的，用户难以通过标定的手段获取灵敏度、静态特性，尤其在使用一段时间后，其灵敏度状态变化用户或使用者不甚清楚；

(2) ICP型、高阻抗输出压电式传感器的低频特性尤其是零频特性比较差[1]，这是由其工作原理决定的；

(3) 毁伤工况下，其工作环境伴随着寄生效应，如热效应、机械冲击、振动等效应，为准确测量冲击波压力，传感器在工作时必须采取隔热、防振等技术措施，而采取了这些技术措施后，必然会引起传感器的等效质量、等效刚度发生变化，导致传感器的灵敏度发生变化，而由厂家提供的裸传感器的灵敏度不再适用这种工况下的传感器组件使用[2-3]。

因此，冲击波压力传感器在使用前，必须对其进行校准。由于压电式压力传感器存在上述诸多问题，采用静态标定方法会产生静态漂移等现象，获得的灵敏度精度不高；基于激波管装置的动态校准方法，激波管的阶跃平台时间不可能做到无穷大[4-5]，无法反映传感器测量系统的零频和低频特性(一般情况下0～800 Hz或0～1 kHz)，更谈不上对冲击波压力传感器实现可溯源的低频校准。故，目前国内外常用基于落锤式液压动标装置的准静态校准方法[6]对压电式冲击波压力传感器进行校准。所谓准静态校准是指用落锤液压动标装置产生类似于半正弦型的压力脉冲对传感器进行动态校准，压力脉冲的有效频带一般在1 kHz以下，而被校冲击波压力传感器的固有频率比较高，可达到100 kHz以上，测量系统的可用频带比较宽，这对于0～1 kHz低频段校准来讲，相当于准静态校准。

准静态校准方法有比对式校准和间接比对式校准两种[7]，其中比对式校准是直接采用“标准传感器”与被校传感器对称地安装在基于落锤液压标定装置的油缸四周的传感器安装孔上，同时监测油缸中的压力，采用“标准传感器”直接对被标定的传感器进行校准。间接比对式校准是当油缸初始容积、活塞有效面积及重锤质量固定不变情况下，对校准用的油缸-重锤组件先用“标准传感器”进行标定，以获得冲击波压力峰值与重锤落高之间的函数关系，然后拆除“标准传感器”，利用上述函数关系，由油缸-重锤组件对被标定的传感器进行校准，实质上是被标传感器与标准传感器进行间接比对，这种标定方法对保护寿命较短而价格昂贵的高压传感器(“标准传感器”)是十分有利的，因此它在测试界被广泛使用。

1 校准方法及试验设计

落锤液压动标装置的工作原理如图1所示。重锤自由下落撞击精密活塞组件，活塞组件压缩造压油缸内的传压介质，产生一个类似于半正弦型压力脉冲。压力Pm可通过调节重锤质量m、落高h、活塞杆有效面积S、造压油缸的初始容积V0等加以改变。

(a)

(b)

考虑到落锤装置产生压力脉冲的影响因素，针对不同的压力校准范围，所对应的油缸初始容积、重锤质量及活塞杆有效面积不同。此外，为消除各落高点的压力随机误差，在每点落高处每次安装都进行n(n≥5)次重复实验，用这些数据的平均值进行建模。

2 冲击波压力传感器间接比对式准静态校准神经网络模型

2.1 RBF神经网络拟合模型设计

RBF神经网络具有很强的非线性逼近能力，通过训练RBF神经网络能够以任意精度近似任意非线性函数[11]。与BP神经网络相比，RBF神经网络不存在局部最优问题。典型的RBF网络结构包括输入层、隐含层和输出层三层。层与层之间采用全互连方式，同一层单元之间不存在相互连接。隐层节点的基函数对输入激励产生一个局部化的响应，输出节点是隐节点基函数的线性组合。

基于RBF神经网络建立的冲击波压力传感器间接比对式准静态校准拟合模型的网络结构如图2所示。

逾越节本是游牧民族一年一度的避祸祈福仪式，意思是降灾的毁灭者越过了困在埃及的以色列子民的房屋，使各家获救。逾越节因此有“拯救”之意。见《摩西五经》，冯象译注，三联书店，2013年版，第134页.

第一层为输入层，只有一个神经元-重锤的落高h。

第二层为隐含层，隐含层节点通过径向基函数将输入空间映射到一个新的空间。目前RBF神经网络常用的基函数为高斯函数。因此，RBF神经网络隐含层第i个节点的输出为

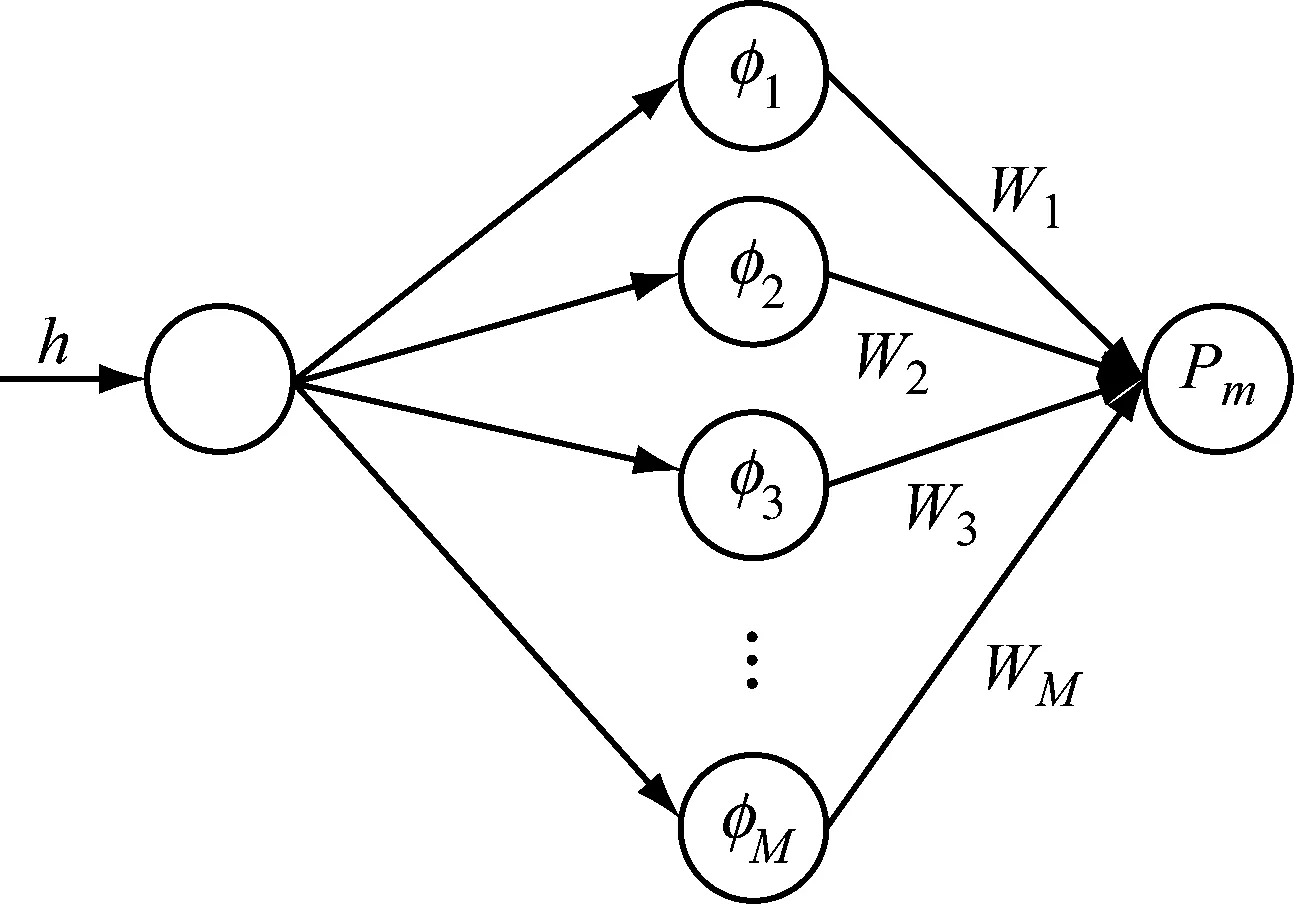
图2 RBF神经网络结构

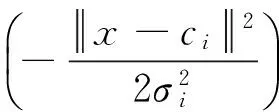
(1)

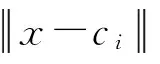
第三层为输出层，也只有一个神经元-冲击波压力峰值Pm，它对隐含层基函数的输出进行线性加权组合，网络输出可表示为

Pm=θ+∑Wiφi

(2)

式中：Wi为隐含层第i个节点与输出层的连接权值；θ为输出节点的偏移。

2.2 网络训练与验证

神经网络结构设计之后，需通过训练样本对神经网络进行学习，网络中待确定参数有两类：①基函数中心ci和宽度σi；②输出层与隐含层之间的连接权值Wi。目前常采用K-均值聚类算法和迭代LMS算法分别学习并确定基函数的中心和宽度，以及输出层与隐含层之间的连接权值。

3 实验分析

某落锤液压动标装置如图3所示，“标准传感器”选用的是四只完全相同的Kistler7005型传感器，量程0～600 bar。在7～30 MPa压力范围的校准实验数据(即神经网络学习的训练样本)如表1所列，给出的压力值Pm均是：单个落高独立重复试验5次，四只“标准传感器”监测结果的平均值。为了进一步检验模型的精度，给出了表2所示的测试样本。

图3 落锤液压动标装置

表1 用于7～30 MPa压力绝对校准建模数据

表2 测试样本

为了提高网络的训练效率，对训练样本进行归一化处理，利用式(3)将表1中数据映射到[0,1]中。

(3)

训练完后，还需利用式(4)将数据进行还原。

(4)

选择落高h作为神经网络的输入层节点，压力Pm作为网络的期望输出，依据2.1节确定的模型，采用Matlab神经网络工具箱编制算法程序进行网络设计、训练和对训练后的网络进行测试。将网络训练目标(Goal)(误差平方和)设置为10-31，在训练过程中调整扩展因子以趋于正确值，做到误差最小。网络训练结果见图4。

由图4可见，实际训练的误差平方和为1.265 34×10-32，实际最终使用了9个神经元节点就已经逼近了训练目标。

最终得出预测效果最好的RBF神经网络预测模型的参数如表3所列。

图4 网络训练结果

表3 RBF神经网络参数设置

(5)

其中，剩余标准差为0.087 9 MPa，线性相关系数为0.999 9。

由于表1的实验数据是在保持重锤质量、造压油液(传压介质)、活塞杆的有效面积以及油缸的初始容积不变的前提下，仅通过改变重锤落高获得的。根据参考文献[6]，Pm与h之间的指数拟合关系如式(6)所示。

Pm=2.325 4h0.515 7

(6)

为了验证构造的神经网络泛化能力，选取了2个测试样本来检验训练精度，测试样本值分别与相应的神经网络拟合值、多项式拟合值及指数拟合值之间的相对误差如表4所示。

由表3的对比结果可见，神经网络模型预测的最大相对误差不超过0.04%，表明文中所建神经网络拟合模型的合理与正确。此外，RBF神经网络拟合值与试验样本值更加接近，RBF神经网络拟合模型的精度比传统的经验公式拟合模型精度高一个数量级。

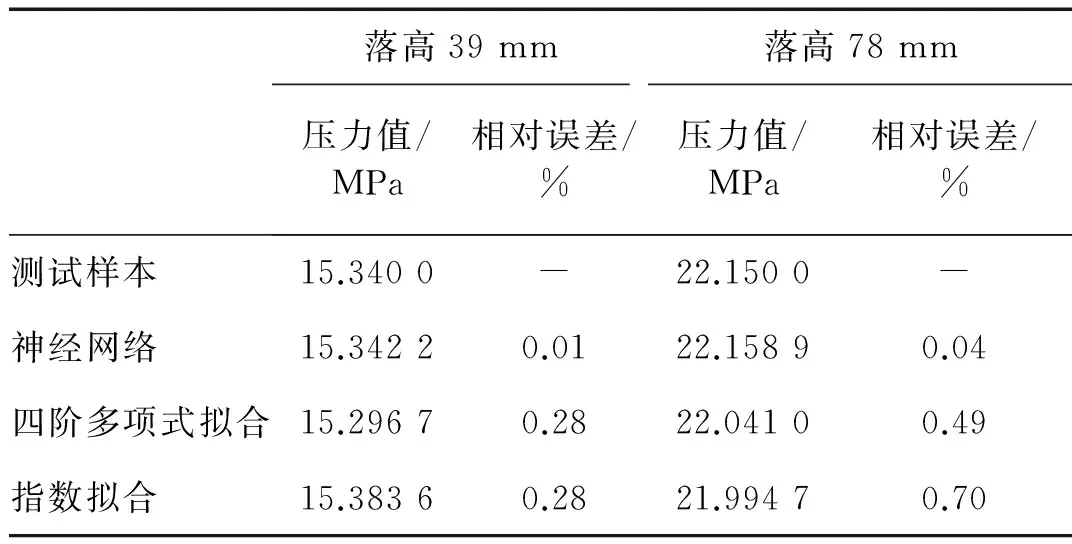
表4 不同方法的计算值

4 结 论

(1) 利用RBF神经网络能够以任意精度近似任意非线性函数的特点，建立了以落高为输入量、压力峰值为输出量的神经网络拟合模型。

(2) 采用测试样本对建立的重锤落高与冲击波压力峰值拟合模型进行检验，结果表明，该神经网络模型预测的最大相对偏差不超过0.04%，四阶多项式拟合模型预测的最大相对偏差不超过0.49%，指数拟合模型预测的最大相对偏差不超过0.70%。可见，神经网络模型的预测精度比传统经验拟合公式的精度高一个数量级。

此外，实验分析神经网络预测模型的训练样本是7～30 MPa压力范围的校准实验数据，因此该神经网络预测模型的动态压力校准范围是7～30 MPa。

[1] XING Qin, ZHANG Jun, QIAN Min. Design, calibration and error analysis of a piezoelectric thrust dynamometer for small thrust liquid pulsed rocket engines[J].Measurement, 2011,44(2):338-344.

[2] 孔德仁, 朱明武, 李永新, 等. 压力传感器准静态“绝对校准”[J]. 传感器技术，2001, 20(12): 32-34.

KONG Deren, ZHU Mingwu, LI Yongxin, et al. Quasi-static absolute calibration on pressure-measuring sensors[J]. Journal of Transducer Technology, 2001, 20(12): 32-34.

[3] 张玉山, 元虎堂. 压电式传感器的准静态校准[J]. 计量与测试技术, 2009,36(1): 33-34.

ZHANG Yushan, YUAN Hutang. Quasi-static calibration method of piezoelectric transducers[J]. Metrology & Measurement Technique, 2009,36(1): 33-34.

[4] 杜红棉,祖静,马铁华,等.自由场传感器外形结构对冲击波测试的影响研究[J].振动与冲击,2011,30(11):85-89.

DU Hongmian, ZU Jing, MA Tiehua,et al. Effect of mount configuration of free-field transducers on shock wave measurement[J]. Journal of Vibration ans Shock, 2011, 30(11): 85-89.

[5] 李强, 王中宇, 王卓然, 等. 压力传感器激波管校准条件下的动态参数估计[J].北京航空航天大学学报, 2015,41(7):1223-1230.

LI Qiang, WANG Zhongyu, WANG Zhuoran, et al. Dynamic parameter estimation of pressure transducer in shock tube calibration test[J].Journal of Beijing University of Aeronautics and Astronautics,2015, 41(7): 1223-1230.

[6] 孔德仁, 朱明武, 李永新, 等. 量纲分析在传感器绝对校准建模中的应用[J]. 弹道学报，2002,14(1):93-96.

KONG Deren, ZHU Mingwu, LI Yongxin, et al. The application of dimension analysis on making absolute calibration model of transducers[J]. Journal of Ballistics, 2002,14(1):93-96.

[7] 孔德仁, 朱明武, 李永新, 等. 基于落锤动标装置的传感器准静态绝对校准方法[J]. 南京理工大学学报, 2002, 26(1): 48-51.

KONG Deren, ZHU Mingwu, LI Yongxin, et al. Means of quasi-static absolute calibration of pressure-measuring transducers based on the drop-hammer dynamic pressure calibration system[J]. Journal of Nanjing University of Science and Technology, 2002, 26(1): 48-51.

[8] 朱明武.压力准静态校准技术[J].宇航计测技术,2004, 24(2): 19-22.

ZHU Mingwu. Pressure quasi-static calibration technology[J].Journal of Astronautic Metrology and Measurement, 2004, 24(2): 19-22.

[9] 狄长安, 孟祥明, 边鹏, 等. 高压压电传感器静态与准静态校准方法研究[J]. 弹道学报, 2014,26(2): 86-89.

DI Changan, MENG Xiangming, BIAN Peng, et al. Analysis on static and quasi-static sensitivity characteristics of high-pressure piezoelectric sensors[J]. Journal of Ballistics, 2014, 26(2): 86-89.

[10] 王丽, 刘训涛. 基于神经网络的压力传感器标定技术[J]. 煤炭技术, 2006,25(7): 109-110.

WANG Li, LIU Xuntao. Calibration of pressure sensor based on neural network[J]. Coal Technology, 2006,25(7): 109-110.

[11] 陈明. MATLAB神经网络原理与实例精解[M]. 北京: 清华大学出版社, 2014.

A neural network model of quasi-static calibration for shock wave pressure sensors

ZHAO Chuanrong1, KONG Deren2, WANG Shengqiang3, SHANG Fei2

1. School of Electrical and Information Engineering, Anhui University of Technology, Ma’anshan 243032, China;2. School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;3. Xi’an Modern Chemistry Research Institute, Xi’an 710065, China)

According to the principle of quasi-static calibration of shock wave pressure sensors, the indirect comparative calibration accuracy depends on the accuracy of the fitting model for pressure versus height of drop-hammer. Here, the RBF neural network was used to set up a neural network model taking height of drop-hammer as input and shock wave pressure peak as output. Choosing a typical standard pressure sensor, the calibration test was performed in the range of 7-30 MPa. Through analyzing test samples, the results indicated that the maximum relative error of the neural network model’s prediction is not more than 0.04%, the accuracy of this model is one order of magnitude higher than those of the polynomial fitting model and the exponential fitting model; the uncertainty induced by the fitting model for pressure versus height of drop-hammer is an important component of the dynamic measurement uncertainty of shock wave pressure sensors; to build a neural network fitting model for shock wave pressure peak versus height of drop-hammer with a higher accuracy can lay a foundation for improving the measurement accuracy of shock wave pressure sensors.

shock wave pressure sensor; RBF neural network; quasi-static calibration; fitting model

国家自然科学基金(11372143)

2015-11-30 修改稿收到日期：2016-05-11

赵传荣 男，博士生,1989年生

孔德仁 男，博士，教授，博士生导师，1964年生 E-mail: derenkongnj@sina.com

O385

A

10.13465/j.cnki.jvs.2017.13.014