基于CDEM的钻地弹侵彻爆炸全过程数值模拟研究

冯 春， 李世海， 郝卫红， 葛 伟

(1. 中国科学院 力学研究所 流固耦合系统力学重点实验室， 北京 100190；2. 晋西工业集团有限责任公司， 太原 030027)

基于CDEM的钻地弹侵彻爆炸全过程数值模拟研究

冯 春1， 李世海1， 郝卫红2， 葛 伟2

(1. 中国科学院 力学研究所 流固耦合系统力学重点实验室， 北京 100190；2. 晋西工业集团有限责任公司， 太原 030027)

提出了一种用于描述岩土介质在冲击载荷下渐进破坏过程的显式数值分析方法(CDEM)。该方法将有限元及块体离散元进行有机结合，利用块体表征材料的弹性、塑性、损伤等连续特征，利用块体间的界面表征裂纹的萌生、扩展及贯通过程。利用CDEM分析了钻地弹的侵彻过程，提出了一种基于破裂度的岩土介质破碎程度评价方法，给出了侵彻面上破碎坑的基本形态及径向裂缝的分布，获得了冲击速度与侵彻深度的正相关关系。数值计算获得的破裂形态及侵彻深度与相关文献的实验及理论分析结果基本一致，证明了所述数值计算方法的正确性。基于一虚拟工况，借助CDEM，分析了钻地弹侵彻及爆炸的双重效应对周边岩体及地下构筑物的影响规律。

钻地弹； 侵彻； 爆炸； 数值模拟； 裂纹扩展； 破裂度

钻地弹是打击敌方重要地下坚固军事目标，如地下掩体、地下指挥所、弹药库、地下发射基地等的有效武器。国内外的专家学者对钻地弹的侵彻能力进行了深入的研究。

在深层侵彻的理论研究中，Sandia国家实验室Forrestal等[1-3]的研究得到国际冲击工程界的公认，Forrestal等通过大量的实验，先后提出了以靶标单轴抗压强度为基础的钻地弹侵彻深度经验预测模型，及基于Mohr-Coulomb准则和最大拉应力准则的球形空腔膨胀模型。陈小伟[4]以Forrestal等的研究为基础，提出了撞击函数I和弹头形状函数N两个无量纲参数，给出了更简便的无量纲刚性弹侵彻/穿甲的终点弹道公式。王明洋等[5]根据短波与岩体的内摩擦模型，利用波阵面上的动量守恒关系和弹体表面的连续运动规律，得到了岩体对弹体的侵彻阻抗，并推导出了侵彻深度的计算公式。Xu等[6]提出了一种基于Hoek-Brown强度准则的弹性-脆性-塑性球形空腔膨胀模型，该模型可以考虑混凝土的应变软化及压力硬化特征。

数值模拟是研究钻地弹侵彻能力的有效手段。目前常用于此类问题模拟的数值方法包括FEM(Finite Element Method)、SPH(Smoothed Particle Hydrod-ynamics)、DDA(Discontinuous Deformation Analysis)及DEM(Discrete Element Method)等，其中，显式动力有限元法(FEM)是进行钻地弹侵彻过程模拟的主流。唐献述等[7]利用LS-DYNA3D对美军GBU-28型钻地弹的侵彻能力进行了模拟，探讨了冲击速度与侵彻深度的对应关系。郑振华等[8]利用LS-DYNA3D研究了钻地弹着速对侵彻深度的影响，并分析了侵彻过程中战斗部装药的过载变化规律。范少博等[9]同样利用LS-DYNA3D探讨了三种不同结构的弹丸和混凝土相互作用的规律,得到了作用过程中三种不同结构弹丸的破坏效能。邓国强等[10]采用TCK(Taylor-Chen-Kuszmaul)模型及JHR(Johnson-Holmquist-Rock)模型分别表述岩体在拉伸及压缩状态下的应力应变关系，并利用有限元软件探讨了非均质岩体中钻地弹重复打击的效果。Tham[11]利用AUTODYN 2D，探讨了纯拉格朗日法(FEM)、拉格朗日欧拉耦合法(钻地弹用FEM描述，靶标用欧拉网格描述)及SPH法(钻地弹用FEM描述，靶标用SPH粒子描述)在模拟钻地弹侵彻深度方面的计算精度；计算结果表明，三种方法均能准确预测出最大侵彻深度，但SPH计算获得的径向应力与实验更为接近。甯尤军等[12]利用2D-DDA对钻地弹侵彻地下岩石隧道的过程进行了模拟，得到了几种不同入侵条件下隧道的稳定性和破坏情况，初步证明了DDA模拟钻地弹侵彻过程的可行性。刘志林等[13]从混凝土的细观结构出发，利用颗粒离散元软件(Particle Flow Code, PFC)进行细观模拟，重点探讨了弹丸受到介质的阻应力与侵彻速度的关系。

本文首先提出了一种FEM/DEM耦合的数值模拟方法CDEM(Continuum Discontinuum Element Method)，而后利用CDEM方法探讨了钻地弹侵彻过程中靶体上的裂纹发展规律及侵彻速度对最终侵彻深度的影响，最后基于一虚拟工况，分析了钻地弹侵彻爆炸的双重效应对地下构筑物的影响。

1 数值方法及计算模型

1.1 CDEM概述

CDEM是连续非连续单元方法[14-15]的英文简称，是一种有限元与离散元耦合的显式数值分析方法，主要用于岩土等材料渐进破坏过程的模拟。该方法的特点是，在模拟材料弹塑性变形的同时，可以模拟显式裂缝在材料中的萌生、扩展及贯通过程。

CDEM中的数值模型由块体及界面两部分构成。块体由一个或多个有限元单元组成，用于表征材料的弹性、塑性、损伤等连续特征；两个块体间的公共边界即为界面，用于表征材料的断裂、滑移、碰撞等非连续特征。CDEM中的界面包含真实界面及虚拟界面两个概念，真实界面用于表征材料的交界面、断层、节理等真实的不连续面，其强度参数与真实界面的参数一致。虚拟界面主要有两个作用：① 连接两个块体，用于传递力学信息；② 为显式裂纹的扩展提供潜在的通道(即裂纹可沿着任意一个虚拟界面进行扩展)。

CDEM中数值模型的示意图如图1所示，该示意模型共包含8个块体，其中有2个块体由2个三角形单元组成，其余的6个块体均由1个三角形单元组成；此外，图1(c)中的虚线为真实界面，实线为虚拟界面。

图1 CDEM中的数值模型构成

CDEM采用基于增量方式的显式欧拉前差法进行动力问题的求解，主要包含节点合力计算及节点运动计算两个部分。节点合力计算如式(1)所示，为

F=FE+Fe+Fc+Fd

(1)

式中：F为节点合力；FE为节点外力；Fe为有限元单元变形贡献的节点力；Fc为接触界面贡献的节点力；Fd为节点阻尼力。

节点运动计算如式(2)所示，为

(2)

式中：a为节点加速度；v为节点速度；Δu为节点位移增量；u为节点位移全量；m为节点质量；Δt为计算时步。基于式(1)、式(2)的交替计算，即可实现显式求解过程。

1.2 有限元部分的求解

采用增量法进行有限元单元应力及节点变形力的计算，为

(3)

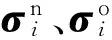
外载荷作用下有限元单元会发生较大的平动及转动，本文通过实时更新应变矩阵(B矩阵)实现单元大变形及大运动的模拟。

1.3 离散元部分的求解

离散元中最重要的两个步骤是接触检测及接触力的计算，本文采用半弹簧-半棱联合接触模型[16-17]进行接触对的快速标记及接触力的精确求解。

半弹簧由单元顶点缩进至各棱(二维)或各面(三维)内形成；半棱仅在三维情况下起作用，由各面面内相邻的半弹簧连接而成。半弹簧形成时，缩进距离一般取顶点到各棱或各面中心距离的1%～5%(本文取5%)。由于半弹簧及半棱找到对应的目标面及目标棱后，方能构建出完整的接触，因此称之为“半”弹簧及“半”棱。

接触对建立后，即可采用增量法进行界面上接触力的计算，为

(4)

式中:Fn、Fs分别为法向、切向接触力；Kn、Ks分别为法向、切向接触刚度；Δdun、Δdus分别为法向、切向相对位移增量。

当进行界面损伤断裂计算时，采用式(5)进行拉伸破坏的判断及法向接触力的修正，为

(5)

式中：T0、T(t0)、T(t1)分别为初始时刻、本时刻及下一时刻界面上的抗拉强度；Ac为界面的面积；εlim为界面的拉伸断裂应变；εp为本时刻界面的拉伸塑性应变，为

(6)

采用式(7)进行界面剪切破坏的判断及切向接触力的修正，为

(7)

式中：φc为界面的内摩擦角;c0、c(t0)、c(t1)分别为初始时刻、本时刻及下一时刻界面上的黏聚力；γlim为界面的剪切断裂应变；γp为本时刻界面上的剪切塑性应变，为

(8)

由式(5)、式(7)可以看出，界面的抗拉强度及黏聚力将随着拉伸塑性应变及剪切塑性应变的增加而线性减小，如图2所示。

(a)(b)

图2 界面上抗拉强度及黏聚力的线性软化效应

Fig.2 Linear softening effect of tensile strength and cohesion in interfaces

当界面上的抗拉强度及黏聚力中的任意一个减小至0时，材料即在界面处发生断裂。

2 钻地弹侵彻过程模拟

2.1 数值模型及参数

对文献[18]中尖卵型实验弹侵彻圆柱形混凝土靶的实验进行模拟。一共进行了两种实验弹(Earth Penetrating Weapon, EPW)的模拟，以下简称实验弹A#(EPW A#)及实验弹B#(EPW B#)。实验弹A#的直径d=25 mm，壁厚ht=3.75 mm(ht/d=0.15)，长度L=150 mm(L/d=6)；实验弹B#的直径及壁厚均与实验弹A#一致，但长度L=250 mm(L/d=10)。为了简化模拟，混凝土靶的尺寸与文献[18]中的略有差异，为φ400 mm×765 mm。考虑到对称性，取1/4模型进行模拟，计算模型如图3所示。其中，实验弹A#共剖分四面体网格41 080个，实验弹B#共剖分四面体网格41 359个。

图3 钻地弹侵彻混凝土靶1/4模型

实验用战斗部的壳体材料为D6A高强度合金钢，参考文献[8]中的本构模型及力学参数，本数值模拟采用Von-Mises理想弹塑性模型进行描述，力学参数如表1所示。

表1 战斗部壳体参数

战斗部壳体内高分子惰性材料采用线弹性模型进行描述，密度为1 650 kg/m3，弹性模量为1.27 GPa，泊松比为0.35。

实验用混凝土靶的单轴抗压强度为45 MPa，采用Mohr-Coulomb模型及最大拉应力模型进行描述。设混凝土的内摩擦角为40°，则根据式(9)，可得该混凝土的黏聚力为10.5 MPa。

(9)

式中：c为黏聚力；σc为单轴抗压强度；φ为内摩擦角。

混凝土实体单元的计算参数如表2所示。侵彻过程中，混凝土实体单元采用溶蚀算法，通过前期试算，取溶蚀应变为4%。

表2 混凝土靶参数

混凝土中各单元间的虚拟界面采用考虑应变软化的Mohr-Coulomb模型及最大拉应力模型，虚拟界面的单位面积法向及切向接触刚度为1014Pa/m，黏聚力、抗拉强度及内摩擦角与实体单元一致(见表2)，拉伸断裂应变为1%，剪切断裂应变为3%。

数值计算时，模型底部法向约束，模型顶部及四周自由，计算时步为0.05 μs，临界阻尼比为3%。实验弹A#的初始侵彻速度为765 m/s，实验弹B#的初始侵彻速度为615 m/s。

2.2 计算结果分析

侵彻深度随侵彻时间的变化规律如图4所示。由图4可得：随着侵彻时间的增大，侵彻深度逐渐增大；当时间为1.2 ms时，实验弹A#基本达到最大侵深(约为38.7 cm)；当时间为2.0 ms时，实验弹B#基本达到最大侵深(约为49.2 cm)。

最大侵彻深度的对比如表3所示。由表3可得，本文数值计算给出的最大侵彻深度与文献[18]中的实验及理论分析的结果基本一致，最大误差小于10%。

图4 侵彻深度随时间的变化

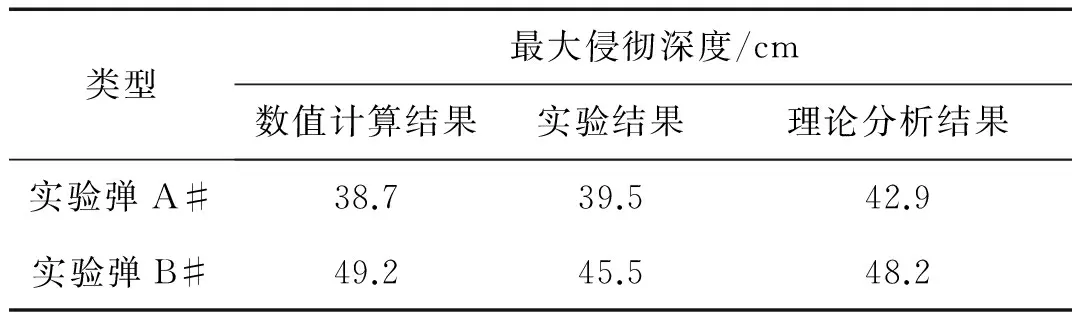
表3 最大侵彻深度的对比

侵彻后混凝土靶标的裂纹发展状态如图5所示。由图5可得，在侵入通道附近出现了密集破碎带，在侵入点附近形成了一定范围的破碎坑，在靶标上表面出现了若干条径向裂缝，在最大倾深所在位置的外侧圆周面附近也出现了若干条裂缝，数值计算所得裂缝发展状况与实验结果(见图6)基本一致。

(a)实验弹A#(b)实验弹B#

图5 靶标裂纹发展状态

图6 实验结果

Fig.6 Experimental result

对裂缝出现的位置及原因进行分析。由于数值模型的底部为法向约束，顶部及四周为自由边界条件。因此，侵入通道附近的密集破碎带主要由钻地弹侵入过程中的强烈挤压作用导致，所产生的裂缝类型为压剪型裂缝；靶标上表面的径向裂缝及外侧壁的缝网主要由钻地弹侵入过程中产生的压应力在自由表面反射生成拉应力导致，所产生的裂缝类型为拉张裂缝。

利用破裂度[19]来表征混凝土的总体破裂情况，定义破裂度为当前时刻破裂的界面数量与数值模型中总界面数量的比值。侵彻过程中，数值模型的破裂度随侵彻时间的变化如图7所示。由图7可得:随着侵彻时间的增加，破裂度逐渐增大；当达到最大侵深后，实验弹处于静止状态，破裂度保持不变；其中，实验弹A#的最终破裂度为6.7%，实验弹B#的最终破裂度为9.4%。

图7 破裂度随时间的变化

3 侵彻速度对最大侵彻深度的影响

3.1 数值模型及参数

模拟文献[3]中CRH 3.0 型钻地弹侵彻混凝土的过程，探讨侵彻速度对最大侵彻深度的影响规律。该型钻地弹的几何尺寸如图8所示。

图8 CRH 3.0 型钻地弹的几何尺寸

该型号钻地弹的总质量为13 kg，混凝土靶标的单轴抗压强度为23 MPa。共进行了6组不同冲击速度的侵彻实验，冲击速度分别为139.3 m/s，200.0 m/s，250.0 m/s，283.7 m/s，336.6 m/s，378.6 m/s。

考虑到对称性，建立1/4数值模型，并剖分22 076个四面体单元。混凝土靶标的直径为0.8 m，高度为1.6 m。数值模型如图9所示。

战斗部采用Von-Mises理想弹塑性模型进行描述，取密度为5 458 kg/m3，弹性模量为80 GPa，泊松比为0.3，抗拉及抗剪强度均为1.7 GPa。

图9 CRH 3.0 型钻地弹侵彻过程数值模型

混凝土单元采用Mohr-Coulomb理想弹塑性模型及最大拉应力模型进行描述，密度为2 520 kg/m3，弹性模量为26.8 GPa，泊松比为0.2，抗拉强度为4.5 MPa，取内摩擦角为40°，黏聚力根据式(9)为5.36 MPa。

混凝土中各单元间的虚拟界面采用考虑应变软化的Mohr-Coulomb模型及最大拉应力模型，虚拟界面的单位面积法向及切向接触刚度为1014Pa/m，黏聚力、抗拉强度及内摩擦角与实体单元一致，拉伸断裂应变为2%，剪切断裂应变为4%。

数值计算时，模型底部法向约束，模型周边全约束，模型顶部自由，计算时步为0.1 μs，临界阻尼比为3%。侵彻过程中，混凝土单元采用溶蚀算法，经过试算，取溶蚀应变为5.6%。

3.2 计算结果分析

最终侵彻深度随侵彻速度的变化曲线如图10所示。由图可得，随着侵彻速度的增大，侵彻深度基本呈线性增大趋势；数值计算获得的侵彻深度变化规律与文献[3]中通过实验获得的规律基本一致(仅在低速及高速段有所差别)，证明了本文所述数值模拟方法的可靠性及计算精度。

图10 侵彻深度随侵彻速度的变化规律

混凝土靶的破裂度随着侵彻速度的变化规律如图11所示。由图11可得:随着侵彻速度的增大，混凝土靶的破裂度逐渐增大，两者基本呈线性关系；当侵彻速度为139.3 m/s时，破裂度约为3.1%；当侵彻速度为378.6 m/s时，破裂度已达8.4%。

不同侵彻速度下，混凝土靶标的裂缝发展情况如图12所示。由图12可得:随着侵彻速度的增大，弹头的侵彻深度逐渐加深；在弹头侵彻路径周边的局部区域，出现了密集的破碎带；在侵入面(上表面)上呈现出了径向裂缝与环向裂缝交错的破裂现象；在剖面上出现了指向侵入面的斜向裂缝，并与侵入面的裂缝带一起构成了具有一定尺寸的破碎坑。

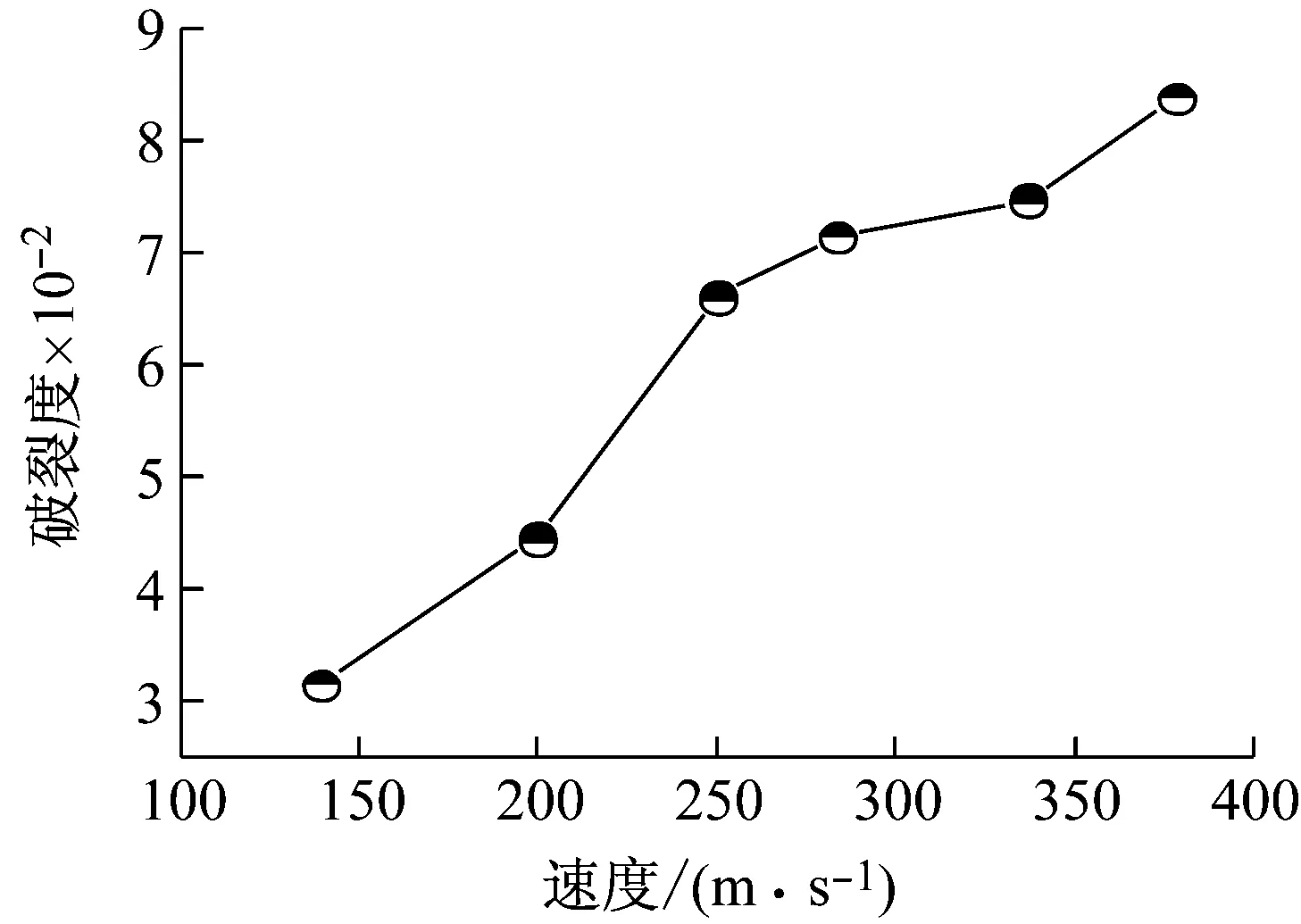
图11 混凝土靶的破裂度随侵彻速度的变化规律

(a)139.3m/s(b)200.0m/s(c)250.0m/s

(d)283.7m/s(e)336.6m/s(f)378.6m/s

图12 混凝土靶上的裂缝

Fig.12 Fractures on concrete target

4 钻地弹的侵彻爆炸过程模拟

4.1 数值模型及参数

设计一钻地弹侵彻爆炸过程的虚拟工况，考察弹头的侵彻爆炸效应对地下构筑物的影响。钻地弹由文献[18]中的A型实验弹放大10倍获得，弹头直径为25 cm，长度为150 cm。为了简化计算，采用二维模型进行定性模拟，共剖分三角形网格71 333个，数值计算模型如图13所示。

图13中，地下构筑物位于地表以下6.25 m，由壁厚30 cm的高强度混凝土(单轴抗压强度138 MPa)封闭而成，构筑物内部空间宽4 m、高3 m。钻地弹的入射速度为700 m/s，入射角度为60°，瞄准点为地下构筑物的左上角(A点)。

图13 钻地弹侵彻爆炸过程的数值模型

该数值模型中的地下构筑物及周边岩体用Mohr-Coulomb准则及最大拉应力准则进行描述，其实体单元的力学参数如表4所示。上述实体单元间的虚拟界面采用考虑应变软化的Mohr-Coulomb模型及最大拉应力模型，虚拟界面的单位面积法向及切向接触刚度为1013Pa/m，黏聚力、抗拉强度及内摩擦角与实体单元一致，拉伸断裂应变为1%，剪切断裂应变为3%。

表4 地下构筑物及岩体的参数

该数值模型中钻地弹的力学模型及力学参数与“2.1”节中的参数一致，此处不再赘述。采用JWL(Jones-Wilkins-Lee)方程描述钻地弹内部炸药的爆炸及爆生气体的膨胀过程，JWL方程可表述为

(10)

式中：P为爆轰产物瞬时压力；V′为爆轰产物相对体积(V/V0)；A1、B1、R1、R2、ω为圆筒试验拟合得出的参数；E0为爆炸产物初始时刻的比内能，J/m3。

本节数值计算采用的炸药参数为，装药密度1 630 kg/m3，炸药比内能7 GJ/m3，实验参数A1为371.2 GPa，B1为3.2 GPa，R1为4.2，R2为0.95，ω为0.3，CJ(Chapman-Jouguet)面上的压力为21 GPa，爆速为7 980 m/s，点火位置为弹头后部，点火时间为触地后16.5 ms。

整个数值模拟共分三个阶段：第一阶段将模型的下边界及左右边界进行法向约束，将钻地弹钝化，进行自重应力场的计算；第二阶段将模型底部及左右两侧的法向约束解除，替换为无反射边界条件，将钻地弹激活，施加700 m/s的冲击速度，进行侵彻过程的计算；当侵彻时间达到16.5 ms时，进行第三阶段的计算，此时钻地弹内部的炸药发生点火起爆，爆生气体对周边岩体及地下构筑物产生冲击破坏。

数值计算时，计算时步设定为0.5 μs，临界阻尼比为3%。侵彻过程中，混凝土单元采用溶蚀算法，溶蚀应变为3%。

4.2 计算结果分析

钻地弹侵彻过程引起的岩体破裂如图14(a)～图14(b)所示。由图14(a)～图14(b)可得：钻地弹在700 m/s的入射速度下快速向岩体内推进，并诱发周边岩体出现多道贯穿地表的裂缝，破裂角(裂缝与水平面的夹角)约为27°，地表破裂半径约为5 m；同时，侵彻产生的冲击应力在地下构筑物的自由面发生了反射，并导致构筑物左侧及上侧附近区域的岩体出现了数条反射拉伸裂缝；由于构筑物采用高强度混凝土建造，反射拉应力并未引起构筑物本身的破坏，但构筑物与围岩的接触面已经发生了脱离。从图中还可以看出，侵彻过程中战斗部发生了逆时针的偏转，偏转角约为12°。

当侵彻16.5 ms(此时侵彻深度约为3.9 m)后，对战斗部进行点火起爆，爆生气体诱发岩体出现了大面积的破坏。战斗部附近的岩体首先出现大量密集的压剪裂缝带；地表附近的岩体在反射拉伸波的作用下出现大量的拉伸裂缝，部分岩体被高速抛起；构筑物左侧及上侧的岩体也出现了大量的反射拉伸裂缝，构筑物左侧及上侧的高强度混凝土在反射拉伸波的作用下出现了明显的拉裂垮塌，具体如图14(c)～图14(e)所示。

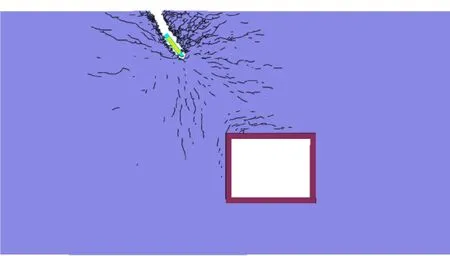
(a) t = 5.47 ms

(b) t =9.47 ms

(c) t = 17.47 ms

(d) t = 21.47 ms

(e) t = 37.47 ms

钻地弹侵彻爆炸过程中，岩体破裂度的演化规律如图15所示。由图15可得，侵彻过程引起的破裂度约为4.5%，而爆炸过程引起的破裂度在18.7%以上。由此表明，钻地弹侵彻后的爆炸效应是诱发岩体破裂及地下构筑物失效的主要原因。

钻地弹侵彻爆炸过程中诱发的构筑物A点、B点(点的位置如图13所示)的振动合速度时程曲线如图16所示。由图16可得:A点的振动幅值明显高于B点，爆炸引起的振动幅值明显高于侵彻引起的幅值；侵彻引起的A点的振动速度幅值为5.4 m/s，B点的振动速度幅值为1.9 m/s；爆炸引起的A点的振动速度幅值为71 m/s，B点的振动速度幅值为20 m/s。

图15 侵彻爆炸过程中的破裂度演化

图16 A点及B点的振动速度时程曲线

5 结 论

(1) 提出了一种有限元与离散元有机结合的显式数值模拟方法CDEM；该方法通过在块体上引入弹塑性本构，实现材料连续介质特性的表达；通过在界面上引入损伤、断裂及接触碰撞模型，实现材料渐进破坏过程的刻画。

(2) 将CDEM应用于钻地弹侵彻爆炸过程的分析，并利用破裂度刻画岩体的毁伤程度。数值计算获得的混凝土破裂形态及侵彻深度与实验结果基本一致，证明了本文所述方法的正确性。

(3) 利用CDEM模拟了钻地弹打击一虚拟地下构筑物的过程。数值结果表明，钻地弹侵彻后的爆炸效应是诱发岩体破裂及地下构筑物失效的主要原因；构筑物的左侧及上侧在爆炸反射拉伸波的作用下出现了明显的拉裂垮塌，并诱发附近的岩体出现了大量的反射拉裂缝。

[1] FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994, 15(4): 395-405.

[2] FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International Journal of Solids and Structures, 1997, 34(31): 4127-4146.

[3] FORRESTAL M J, FREW D J, HICKERSON J P, et al. Penetration of concrete targets with deceleration-time measurements[J]. International Journal of Impact Engineering, 2003, 28(5): 479-497.

[4] 陈小伟. 动能深侵彻弹的力学设计(I)：侵彻/穿甲理论和弹体壁厚分析[J]. 爆炸与冲击, 2005, 25(6):499-505.

CHEN Xiaowei. Mechanics of structural design of EPW(I):the penetration /perforation theory and the analysis on the cartridge of projectile[J]. Explosion and Shock Waves, 2005, 25(6):499-505.

[5] 王明洋, 谭可可, 吴华杰,等. 钻地弹侵彻岩石深度计算新原理与方法[J]. 岩石力学与工程学报, 2009, 28(9):1863-1869.

WANG Mingyang, TAN Keke, WU Huajie, et al. New method of calculation of projectile penetration into rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(9):1863-1869.

[6] XU H, WEN H M. A spherical cavity expansion penetration model for concrete based on Hoek-Brown strength criterion[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2012, 13(2): 145-152.

[7] 唐献述, 周翔. 美军某型钻地弹侵彻能力数值模拟研究[J]. 弹箭与制导学报, 2004, 24(2):311-313.

TANG Xianshu, ZHOU Xiang. Research on a type of earth penetration weapon of US army by numerical simulation[J]. Journal of Projectiles Rockets Missiles and Guidance, 2004, 24(2):311-313.

[8] 郑振华, 余文力, 王涛. 钻地弹侵彻高强度混凝土靶的数值模拟[J]. 弹箭与制导学报, 2008, 28(3):143-146.

ZHENG Zhenhua, YU Wenli, WANG Tao. Numerical analysis of the EPW penetration into high strength concrete target[J]. Journal of Projectiles Rockets Missiles and Guidance, 2008, 28(3):143-146.

[9] 范少博, 陈智刚, 郭光全,等.新型旋进侵彻钻地弹数值模拟[J]. 中北大学学报(自然科学版), 2013, 34(2): 128-133.

FAN Shaobo, CHEN Zhigang, GUO Guangquan, et al. Simulation on a novel rotated penetrating projectile[J]. Journal of North University of China(Natural Science), 2013, 34(2): 128-133.

[10] 邓国强, 杨秀敏. 工程岩体中多弹重复打击效应的数值模拟分析[J]. 爆炸与冲击, 2014, 34(3):361-366.

DENG Guoqiang, YANG Xiumin. Numerical simulation of the effect of multiply EPW into engineering rock[J]. Explosion and Shock Waves, 2014, 34(3):361-366.

[11] THAM C Y. Numerical and empirical approach in predicting the penetration of a concrete target by an ogive-nosed projectile[J]. Finite Elements in Analysis and Design, 2006, 42(14): 1258-1268.

[12] 甯尤军, 杨军. 钻地弹侵彻地下结构的2D-DDA模拟研究[J]. 战术导弹技术, 2006(5):39-43.

NING Youjun, YANG Jun. Smiulation study of earth penetrator penetrating underground structures with the Method of 2D-DDA[J]. Tactical Missile Technology, 2006(5):39-43.

[13] 刘志林, 孙巍巍, 王晓鸣. 基于颗粒流离散元模型的弹丸侵彻细观混凝土数值模拟方法研究[J]. 振动与冲击,2016, 35(4): 162-169.

LIU Zhilin, SUN Weiwei, WANG Xiaoming. Numerical simulation for projectile penerating meso-scale concrete based on particle flow discrete elment model[J]. Journal of Vibration and Shock, 2016, 35(4): 162-169.

[14] LI S H, WANG J G, LIU B S, et al. Analysis of critical excavation depth for a jointed rock slope using a face-to-face discrete element method[J]. Rock Mechanics and Rock Engineering, 2007, 40(4): 331-348.

[15] WANG Y N, ZHAO M H, LI S H, et al. Stochastic structural model of rock and soil aggregates by continumm-based discrete element method[J]. Scinece in China Series E-Engineering & Materials Science, 2005, 48 (Supl):95-106.

[16] 冯春,李世海,刘晓宇.半弹簧接触模型及其在边坡破坏计算中的应用[J]. 力学学报, 2011, 43(1): 184-192.

FENG Chun, LI Shihai, LIU Xiaoyu. Semi-spring contact model and its application to failure simulation of slope[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 184-192.

[17] FENG C, LI S H, LIU X Y, et al. A semi-spring and semi-edge combined contact model in CDEM and its application to analysis of Jiweishan landslide[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2014, 6(1): 26-35.

[18] 陈小伟, 张方举, 杨世全,等.动能深侵彻弹的力学设计(III):缩比实验分析[J]. 爆炸与冲击, 2006, 26(2): 105-114.

CHEN Xiaowei, ZHANG Fangju, YANG Shiquan, et al. Mechanics of structural design of EPW(III): investigations on the reduced scale tests[J]. Explosion and Shock Waves, 2006, 26(2): 105-114.

[19] 李世海, 周东, 刘天苹. 基于破裂度的堆积层滑坡危险性分析方法[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3909-3917.

LI Shihai, ZHOU Dong, LIU Tianping. Risk analysis method of accumulated landslide based on fracture degree[J]. Chinese Journal of Rock Mechanics and Engineering， 2013, 32(Sup2): 3909-3917.

Numerical simulation for penetrating and blasting process of EPW based on CDEM

FENG Chun1, LI Shihai1, HAO Weihong2, GE Wei2

(1. Key Laboratory for Mechanics in Fluid Solid Coupling Systems, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China； 2. Jinxi Industries Group Co., Ltd., Taiyuan 030027, China)

To simulate a progressive failure process of rock and soil under impact loads, an explicit numerical analysis method named CDEM was proposed. In this method, FE and block DE were well combined. Blocks were used to characterize elastic, plastic and damage features of materials. Interfaces among blocks were adopted to characterize processes of crack initiation, propagation and penetration. With CDEM, the penetrating process of an EPW was analyzed, and an evaluation method for rock and soil crushing degree based on the fracture degree was proposed. The basic pattern of crushing pits and the distribution of radial cracks on a penetrating surface were deduced, and the positive correlation between impact velocity and penetrating depth was gained. It was shown that the numerical results of crushing pattern and penetrating depth agree well with those of tests and theoretical analysis in references to verify the correctness of CDEM. Finally, based on a virtual case, the penetrating and blasting effects of an EPW on the surrounding rocks and underground structures were analyzed using CDEM.

earth penetrating weapon (EPW); penetrating; blasting; numerical simulation; crack propagation; fracture degree

中国科学院战略性先导科技专项 (XDB10030303)；国家自然科学基金青年基金(11302230)

2016-01-25 修改稿收到日期：2016-05-15

冯春 男，硕士，高级工程师，1982年生

李世海 男，博士，研究员，博士生导师，1958年生

O389

A

10.13465/j.cnki.jvs.2017.13.002