化归思想在初中数学教学中的实践研究

谢守君

摘 要：随着数学教学改革进程的不断推进，数学化归思想在初中数学教育中的地位不断上升，这其中的原因多在于化归思想的作用。化归思想可以使学生理解抽象地、复杂地问题，并运用一定的思想工具将问题具体归类，进行一定程度上的处理。站在数学教学发展的角度上来说，数学化归思想的初步建立，有助于帮助学生建立数学逻辑思维与学习架构，从而提升学生的数学学习能力与学习兴趣，推进初中数学课堂教学效率的提升。因此，本文将就化归思想在初中数学教学中的实践，作为本文的立足点，结合本人多年地教学实际，对化归思想在教学的实际应用进行一个初步地探索与分析。

关键词：化归思想；初中数学；教学发展

现在初中数学教学走到了一个瓶颈期，原因在于原有的解题技法性教学不再适用于教学实际，不适用于追求学生综合素质教育的当下。因此，初中数学教学为了提高教学效率与教学质量就必须要进行教学目标上的优化发展，数学思想教学也就因此得以渗透进教学中。作为教师，运用数学思想进行教学有助于提高教学质量；而作为学生，接受数学思想的教学，有助于自身理解数学理论在实际运用中的变化，从而将复杂地问题简单化。下文将就数学思想中的化归思想做以展开，讲解探究如何在初中数学课堂教学中，渗透进化归思想教学。

一、数学教学中运用化归思想将陌生问题熟悉化

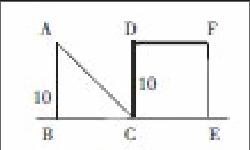
初中数学作为数学学习的基础期，其中的知识涉及了大量地数学原理与内涵，这就使得数学问题有着大量地变化可能。也正是因此，数学知识的学习是一个熟悉化的过程。对于初中学生而言，一道题型如果是自己所熟悉的，那么解题不会遇到障碍，但如果内涵一致，题型有变，就会对解题造成困扰。例如：在教学“三角形的三边关系”这一知识点时，有一道题，如图1所示，等腰三角形ABC以2m/s的速度沿着直线方向移动，直至AB与CD重合，如果运动x秒，三角形与正方形的重叠部分为面积ym2，最后求X与Y的关系。

在这一问题中，学生掌握了三角形三边关系的知识点，但这是一种静态的掌握，仅能依靠图形、已知条件来解决问题，对具有动点的问题就显得无能为力。而教师引导学生运用化归思想，引导着学生将动点相关地线段标注出来，并代入公式，就可以将这一动态化的问题，转化为学生已经掌握的静态题型。从此处就可以发现，化归思想是有助于学生掌握数学问题转化方法的，从这一角度讲，化归思想有助于提高学生将陌生问题熟悉化的能力。

二、数学教学中运用化归思想将抽象问题具体化

化归思想作为数学逻辑思维中的一种，其具体表现为使用者可以借助这一思想工具，将抽象化地数学问题进行一个具体化的处理。换言之，这一数学思想在数学教学中，是帮助学生对复杂地逻辑问题进行整理的思想工具。例如：在教学“一次函数”这一知识点时，由于学生是首次接触这种具有变量的数学问题，会感觉此类型问题过于抽象，而感到无从下手。此时，作为教师就应当以生活中所具有地情景，结合数学化归思想，为学生提供一个前置地教学情景。如：“手机套餐资费收费情况”。这一问题是学生日常生活中经常接触的一个问题，此问题可以调动学生的学习积极性，且由于资费变化的形式与一次函数较为相像，可以借此进入教学环节，与学生共同探讨。一般地，教师可以从以下问题入手：①每月资费受哪些因素影响；②影响资费的通话时间有哪些？

在教师对学生进行了化归思想教学的情况下，学生会优先考虑套餐资费与内容间的函数表达式，并试着去解释，所得函数的表达式中的一次项系数和常数项的实际意义。在这一问题情境中，生活中常见地问题被转化为了函数问题，这是得益于化归思想的运用。也正是因为化归思想，使得学生可以依靠数学知识来解决实际问题，并对抽象化地问题进行一个归纳总结，并转化为一个较为可靠及可理解的具体问题。从这一角度上来说，数学思想工具的学习对于学生逻辑思维能力的构建是极有帮助的。

三、数学教学中运用化归思想将公理化为已知条件

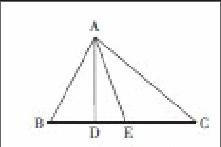
在我国数学教学中，数学问题的解决依赖于数学公式与公理，这二者的学习与运用为学生在实际问题中，有效率地解决问题提供了方法与便利。例如：教师应当在教学中渗透化归思想，帮助学生在掌握公理后，面对实际数学问题可以将公理条件化。如图2所示，在三角形ABC中，AD是BC边上的高，AE平分∠BAC，∠B、∠C分别为75°、45°，求角∠DAE与∠AEC的度数。

以此题为例，题目中并未提及外角定理，但这并不意味着学生不能使用定理，学生通过运用定理，可以迅速地转化为已知条件，从而应用到解题中去。在这一案例中，学生掌握了外角定理与数学化归思想，就获得了较为快速地解题方法。在这一角度上来说，化归思想可以帮助学生在掌握数学定理的基础上，加快解题进度。因此，学生在掌握化归思想的基础上，必然地对数学定理的学习与掌握有一个学习欲望，这有助于学生自主学习能力与欲望的提高。

四、结语

化归思想在数学逻辑思想工具中是极为基础，却又极为重要地一个数学工具。学生在掌握化归思想后，就具有了运用数学思想发现问题本质的能力，从而使自身可以运用数学知识来解决实际问题，做到知行合一。也因为培养学生综合素质的需要，教师就必须在教学中合理、科学地渗透进化归思想，并在教学实践过程中，结合教学内容与学生学习特点的实际，将化归思想渗透进学生思维中，并引导着学生建立以化归思想为基础的数学逻辑框架，并运用这一框架将数学问题简单化、具体化，从学生学习能力培养这一角度，降低數学问题的难度，以培养学生数学科目的学习兴趣。为了达成这一教学目的，教师在教学中就不应拘泥于形式，并将自己定位成一个教学引导者，而非开拓者。在教学过程中锻炼学生的数学研究能力，只有这样才能在数学教学中培养学生数学学习能力与思想的良性发展，并借助数学教学推动学生综合素质的全面发展。

参考文献：

[1]谢德荣.论化归思想在初中数学教学过程中的应用研究[J].中学生数理化：学研版，2012（5）：88-88.

[2]荀炳义.化归思想在初中数学课堂教学中的实践研究[J].理科考试研究：初中版，2015，22（8）：20-20.endprint