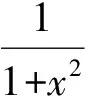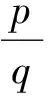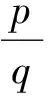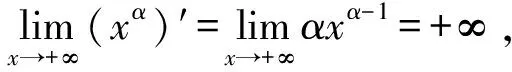基本初等函数的一致连续性

王金花,樊永艳,李志晓

(沧州师范学院数学与统计学院，河北沧州061001)

基本初等函数的一致连续性

王金花,樊永艳,李志晓

(沧州师范学院数学与统计学院，河北沧州061001)

基本初等函数：常值函数y=c，幂函数y=xa，对数函数y=logax(0

连续；一致连续；基本初等函数；函数可导

函数的一致连续性是数学分析课程的重要理论，数学分析课程中的很多重要结论的证明都要用到函数的一致连续性.目前很多数学工作者对函数的一致连续性进行研究，并得到重要结论.数学分析的研究对象是函数，初等函数的分析性质是数学分析的重要研究内容，而初等函数是由基本初等函数经过有限次四则运算与有限次复合所得到的函数[1](P14-15)，所以研究基本初等函数的分析性质尤为重要，下面探讨基本初等函数的一致连续性．

1 预备知识

定义1 设函数f(x)在区间I上有定义，若任意ε>0，存在δ=δ(ε)>0，使得对任意的x1,x2∈I，只要|x1-x2|<δ时，就有|f(x1)-f(x2)|<ε，则称函数f(x)在区间I上一致连续[1](P79)．

定理1 设f(x)在区间I上可导，且f′(x)有界,则f(x)在I上一致连续[2][3]．

定理2 若f(x)在有限闭区间[a,b]上连续，则f(x)在[a,b]上一致连续[1](P80)．

所以f(x)在(a,+∞)上不一致连续．

类似可证下面的定理4：

证明从略．

利用函数一致连续的定义，容易推得下面的定理5成立．

定理5 若f(x)在区间I上一致连续，区间I1⊂I，则f(x)在I1上一致连续．

证明从略．

定理7 一切基本初等函数都是其定义域上的连续函数[1](P84)．

定理8 若函数f(x)在区间I1和I2上一致连续，且I1与I2有公共点，则f(x)在I1∪I2上一致连续[1](P80)．

2 主要结论

下面讨论基本初等函数的一致连续性．

2.1 常值函数y=c

由于y′=0在(-∞,+∞)上有界，由定理1知道，常值函数y=c在(-∞,+∞)上一致连续．

2.2 反三角函数

函数y=arcsinx与y=arccosx是[-1，1]上的连续函数．由定理2知道，y=arcsinx与y=arccosx在[-1,1]上一致连续．

2.3 三角函数

对于正弦和余弦函数y=sinx、y=cosx，由于|(sinx)′|=|cosx|≤1，|(cosx)′|=|-sinx|≤1．由定理1知道，y=sinx与y=cosx在(-∞,+∞)上一致连续．

2.4 幂函数

随着实数α的不同，幂函数y=xα的定义域不同．

当α为正无理数时，y=xα的定义域是[0,+∞)；当α为负无理数时，y=xα的定义域是(0,+∞)．

(1)当0<α≤1时，y=xα的定义域为(-∞,+∞)或[0,+∞)．由于(xα)′=αxα-1在[1,+∞)上有界，由定理1知道，y=xα在[1,+∞)上一致连续，又由定理2、定理7和定理8知道，y=xα在[0,+∞)上一致连续．当y=xα的定义域为(-∞,+∞)时，α为有理数，y=xα为奇函数或偶函数，在(-∞,1]∪[1,+∞)上，(xα)′=αxα-1有界，由定理1知道，y=xα在(-∞,1]和[1,+∞)上一致连续，又由定理2、定理7和定理8知道，y=xα在(-∞,+∞)上一致连续．

(2)当α=0时，y=xα=1为常值函数，在(-∞,+∞)上一致连续．

2.5 指数函数

2.6 对数函数

综上所述，对于六类基本初等函数，其中常值函数、反三角函数、正弦函数、余弦函数、幂函数y=xα(0≤α≤1)在其定义域上一致连续，其它的基本初等函数在其定义域区间上非一致连续．

[1] 华东师范大学数学系.数学分析(第四版)[M].北京：高等教育出版社，2001．

[2] 甘宗怀，李秋林．关于可导函数一致连续性的判定定理[J]．高师理科学刊，2009，29(5)：38-39．

[3] 王文华，曹怀信．一元函数一致连续性的性质[J]．榆林学院学报，2016,26(4)：31-34．

[4] 钱吉林.数学分析题解精粹(第二版)[M]．武汉：湖北长江出版集团崇文书局，2011．

[责任编辑：刘秀敏]

Uniform Continuity of Basic Elementary Functions

WANG Jin-hua, FAN Yong-yan, LI Zhi-xiao

(College of Mathematics and Statistics, Cangzhou Normal University, Cangzhou, Hebei 061001, China)

The concept of uniformly continuous function, some sufficient conditions and necessary conditions are introduced. Sequentially, the uniform continuity of basic elementary functions is discussed.

continuity; uniform continuity; basic elementary functions; derived function

2016-11-28

王金花(1963-)，女，河北河间人，沧州师范学院数学与统计学院副教授，研究方向：非线性泛函分析； 樊永艳(1982-)，女，河北孟村人，沧州师范学院数学与统计学院讲师，研究方向：微分方程及边值问题； 李志晓(1990-)，女，山东乐陵人，沧州师范学院数学与统计学院助教，研究方向：统计分析.

O171

A

2095-2910(2017)02-0001-03