一类超幂幺半群的结构

王春茹,邹佩,狄明

(西安建筑科技大学华清学院,陕西 西安 710043)

王春茹,邹佩,狄明

(西安建筑科技大学华清学院,陕西 西安 710043)

U-半富足半群和 U-富足半群是富足半群的推广,作为富足半群的一种推广,超幂幺半群是超富足半群的子类,文章引入本原 U超富足半群的定义,得到了幂幺半群的结构定理.

U-超富足半群;完全单半群;强半格

1 引言和准备

假设S是一个半群,E(S)是半群S的幂等元集.U是E(S)的非空子集.在半群S上定义Green关系如下:

2 定义和引理

定义 2.1设S为半群,称S为带,如果S中每个元素均为幂等元,即对于任意a∈S,有a2=a,那么称S为带.

定义 2.2设 Y为半格,{Sα:α∈Y}为用 Y加标的互不相交的半群族.对于任意 α,β ∈Y 使得 α>β,存在同态 ϕα,β:Sα→Sβ,使得

(i)(∀α ∈ Y)ϕα,α=1Sα.

(ii)任取 α,β,γ ∈Y 使得 α ≥ β ≥ γ,

那么(S,∗)将成为半群.把这个半群称为半群Sα的强半格,ϕα,β称为结构同态,记为

定义 2.3半群S称为单半群,如果为S上的泛关系.U-富足半群S称为完全单半群,如果S为U-超富足的，且为单.

推论 2.1如果半群S是富足半群,当且仅当对于任意a∈S,存在幂等元e,f∈S,使得

成立.

推论 2.2如果e是半群S的幂等元,对于任意a∈S,下面几款等价:

引理 2.1如果S中的每一个L∗-类和每一个R∗-类都含有幂等元,半群S称为富足半群.

定义 2.4若S中的每一个类和每一个类都含有幂等元,(S,U)称为U-半富足半群.

定义 2.5若(S,U)是半富足的且是右同余,是左同余,(S,U)称为U-富足半群.

定义 2.6如果每一个类中含U中的元素,U-富足半群S称为U-超富足半群.

引理 2.2幂等元e∈S是本原的,如果存在幂等元f∈S有f 6 e,则

否则f=e.若S中的每个幂等元都是本原的,则称半群S是本原的.

定义 2.7[3-4]半群 (S,U)是本原的,在类中,如果 (S,U)中的每一个非零投射元e是本原的.

引理 2.3[5-6]S是一个半群,E(S)是S中的幂等元集,U⊆E(S).对于任意a∈(S,U),e∈U,有

引理 2.4本原U-富足半群,e是(S,U)中的非零投射元,则当且仅当a∈Se(a∈eS).

证明必要性假设则

3 主要结果

定理 3.1在半群(S,U)上,下面几个是等价的:

证明(i)⇒(ii)显然.

(ii)⇒(iii)易知,(S,U)是U-超富足半群.对于任意a,b∈(S,U),如果则

有

因此eS⊆Se,所以,对于任意

是从S1到eS1的半群同态.

(iv)⇒(v) 首先证明(S,U)是U-超富足半群.任意

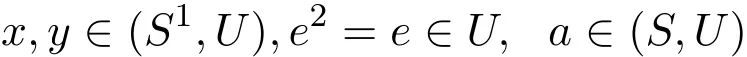
有

因此eS⊆Se因为(S,U)是U-富足半群,对于任意a∈(S,U),存在一个投射元e∈(S,U),使得根据引理 2.3和(S,U)是本原的,可得

参考文献

[1]Fountain J B.Abundant semigroups[J].London Math.Soc.,1982,44(3):103-129.

[2]Howie J M.An Introduction to Semigroup Theory[J].Amercia:Academic Press,1976.

[3]Ren X M,Shum K P.Guo Y Q.On Super R∗-Unipotent Semigroups[M].Southeast Asian Bulletin of Mathematics,1998,22:199-208.

[4]Ren X M,Shum K P.The structure of superabundant semigroups[J].Science China Series A Mathematics,2004,47(5):756-771.

[5]Ren X M,Shum K P.Structure theorems for right pp semigroups with left central idempotents[J].General Algebra and Applications,2000,20:63-75.

[6]Shum K P,Ren X M.Abundant semigroups with left central idempotents[J].Pure Math.Appl.,1999,10(1):109-113.

The structure of super-unipotent semigroups

Wang Chunru,Zou Pei,Di Ming
(Huaqing College,Xi′an University of Architecture and Technology,Xi′an 710043,China;)

The U-half abundant semigroups and U-abundant semigroup is the promotion of the abundant semigroup.As a generalization of the abundance semigroup,superunipotent semigroups is the subclass of abundant semigroups.we introduce the de fi nition ofprimitive U-abundant semigroups.And later on,we obtain some characterizations of superunipotent semigroups.

U-superabundant semigroups,completelysimple semigroups,primitive

O152.7

A

1008-5513(2017)03-0326-05

10.3969/j.issn.1008-5513.2017.03.012

2017-03-13.

国家自然科学基金(11471255);陕西省教育厅基金(15JK1411);校级基金(17KY02).

王春茹(1983-),硕士,讲师,研究方向:半群代数理论.

2010 MSC:08A05