G-度量空间中次相容映象对的公共不动点定理

张倩雯,谷峰

(杭州师范大学数学系,浙江 杭州 310036)

G-度量空间中次相容映象对的公共不动点定理

张倩雯,谷峰

(杭州师范大学数学系,浙江 杭州 310036)

在G-度量空间中,引入了映象对次相容和相对连续的概念,并使用这些概念,证明了几个新的公共不动点定理.本文结果拓展和改进了之前文献中一些相关结果.

G-度量空间;相容;次相容;相对连续;次序列连续;公共不动点.

1 引言

文献[1]引入广义度量空间的概念,简称G-度量空间,它是度量空间的推广.文献[2]首次在G-度量空间中研究公共不动点问题.后来,文献[3]在G-度量空间中引入了映象对弱交换和R-弱交换的概念,并得到了一些公共不动点结果.文献[4]在G-度量空间中引入了相容映象和(A)型相容映象的概念,证明了几个公共不动点定理.文献[5-6]研究了G-度量空间中弱相容映象的一些公共不动点问题.

文献[7]在度量空间中证明了几个有关次相容映象和次序列连续映象的公共不动点定理.文献[8]修正了文献[7]中的一些错误,证明了几个新结果.受文献[7]和[8]的启发,我们在G-度量空间中引入了映象对次相容和相对连续的概念,证明了几个新的公共不动点定理,将文献[8]中的结果推广到G-度量空间中,从而拓展了他们的成果.

在介绍主要结果之前,先给出有关G-度量空间中的一些基本概念.

定义 1.1[1]设X是一个非空集合,X×X×X→R+为一函数,且满足以下条件:

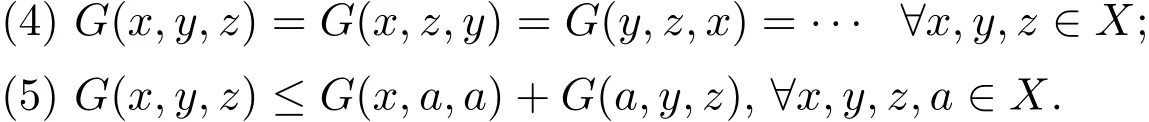
则称函数G是X上的一个广义度量,或简称为X上的一个G-度量,并称(X,G)是一个广义度量空间,简称为G-度量空间.

定义 1.2[1]设(X,G)为一G-度量空间,{xn}为X中的一个序列,X中的点x称为序列{xn}的极限或称序列{xn}G-收敛到x,如果

定义 1.3[1]设 (X,G)和 (X′,G′)是两个 G-度量空间,函数 f:(X,G)→(X′,G′).称 f在点a∈X 处是 G-连续的,如果对于任意的 ε>0,存在 δ>0使得对任意的 x,y∈X,G(a,x,y)<δ,有G′(f(a),f(x),f(y))<ε.如果 f在 X 上每一点处都是 G-连续的，则称f在X上是G-连续的.

命题 1.1[1]设(X,G)为一G-度量空间,则函数G(x,y,z)关于这三个变量连续.

命题 1.2[1]设 (X,G)和 (X′,G′)是两个 G-度量空间,则 f:X → X′在点 x∈X处G-连续当且仅当f在x处是G-序列连续的,即若{xn}G-收敛到x,那么{f(xn)}G-收敛到f(x).

定义 1.4[4]G-度量空间(X,G)中的自映象对f与g称为是相容的,若对任意的{xn}⊂X,只要

就有

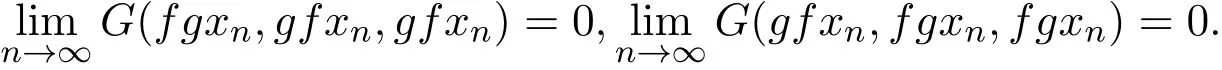
文献[9]在度量空间中提出了映象对相对连续的概念.文献[8]提出了度量空间中映象对次相容和次序列连续的概念.下面把这些概念引入到G-度量空间中.

定义 1.5G-度量空间 (X,G)中的自映象对 f与 g称为是相对连续的,若对任意的 {xn}⊂X,只要

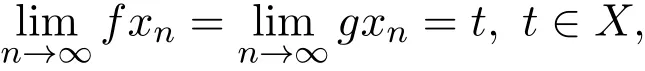
就有

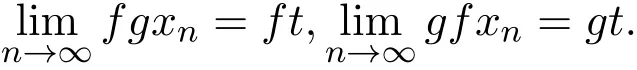
定义 1.6G-度量空间 (X,G)中的自映象对 f与 g称为是次序列连续的,若存在 {xn}⊂X,使得

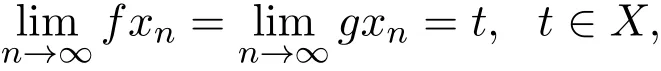
则有

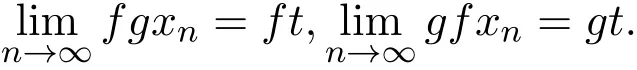
注 1.1易知,连续的映象对一定是相对连续的,反之不真.连续或者相对连续的映象对一定是次序列连续的,但是存在次序列连续的映象对既不是相对连续的也不是连续的.反例如下:

例 1.1设X=[0,∞),(X,G)是一个G-度量空间.定义映象f,g:X→X 如下:

由此可见映象对f与g是次序列连续的,但不是相对连续的,也不是连续的.

定义 1.7G-度量空间(X,G)中的自映象对f与g称为是次相容的,若存在X中的序列 {xn},使得

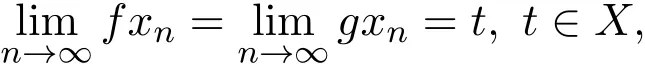
有

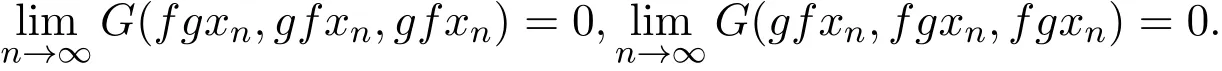
注 1.2易知,相容的映象对一定是次相容的,反之不真.反例如下:

例1.2令X=R,G是X上的任意一个G-度量.定义映象f,g:X→X如下:

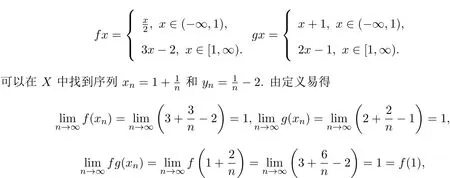
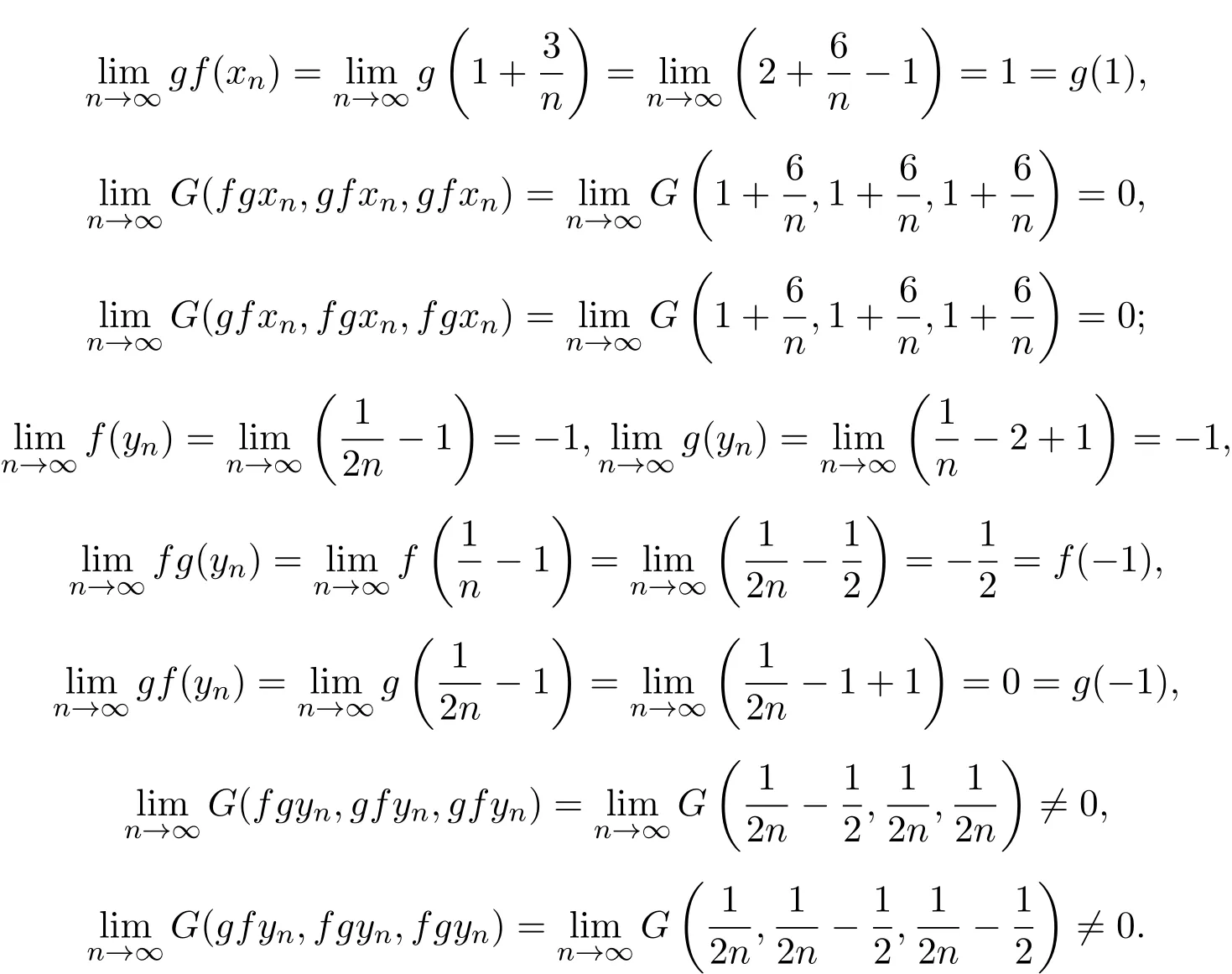
这说明映象对f与g是次相容的,且是相对连续的,但不是相容的,也不是连续的.

2 主要结果

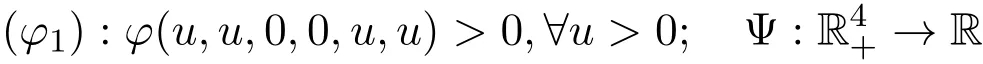
是一个下半连续函数,满足(Ψ1):Ψ(u,u,u,u)>0,∀u>0.本文中提及的φ和Ψ都如上所述.

定理 2.1设f,g,h和k是G-度量空间(X,G)中的四个自映象,若映象对(f,h)和(g,k)都是次相容和相对连续的,则

(a)f和h有重合点; (b)g和k有重合点.

此外,如果∀x,y∈X,有以下不等式成立

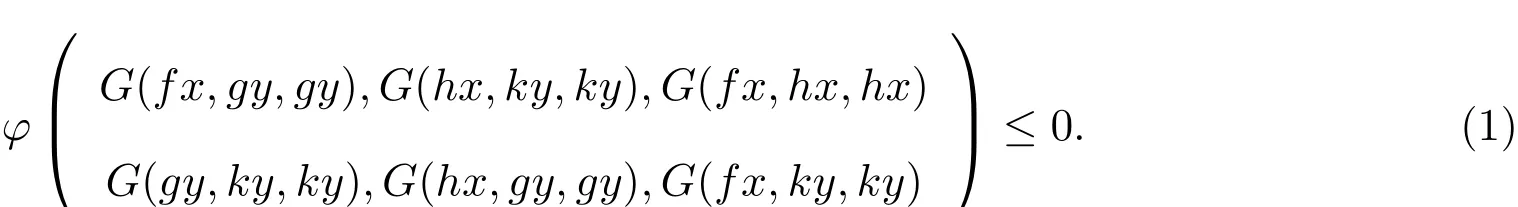
则f,g,h和k有唯一公共不动点.

证明先证f和h有重合点,g和k有重合点.事实上,因映象对(f,h)和(g,k)都是次相容和相对连续的,所以存在{xn},{yn}⊂X,t,t′∈X,使得

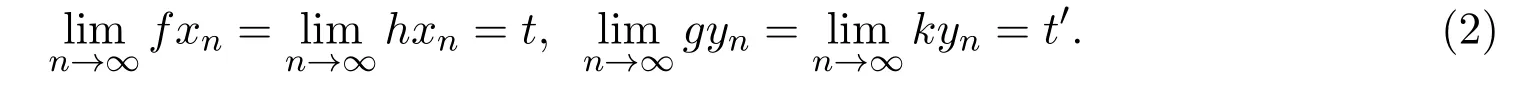
且

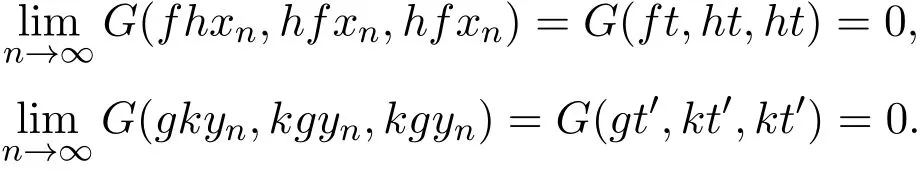
因此

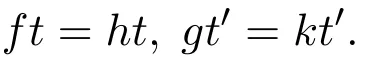
即t是f和h的重合点,t′是g和k的重合点.

现在证 t=t′.由 (1)式可得

在上式中令n→∞,并使用φ的下半连续性,可得

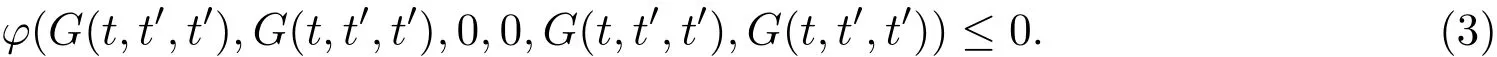
若 G(t,t′,t′)>0 则式 (3) 式与 (φ1) 矛盾,因此 G(t,t′,t′)=0,即 t=t′.

再证ft=t.由(1)式可得

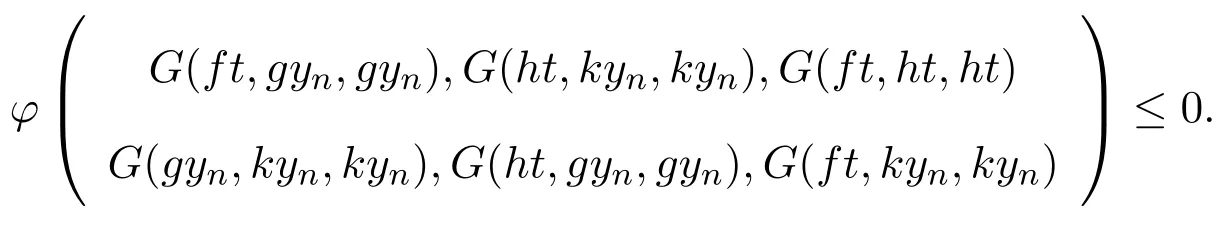
在上式中令n→∞,并使用φ的下半连续性,ft=ht以及t=t′,可得

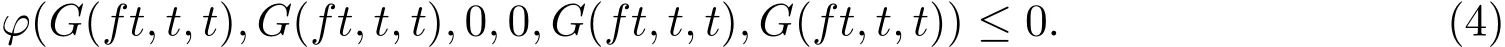
若 G(ft,t,t)>0,则式 (4)与 (φ1)矛盾,因此 G(ft,t,t)=0,即 ft=t.

同理可证gt=t.所以有

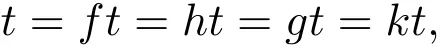
即t是映象f,g,h和k的公共不动点.

下证唯一性.假设z是映象f,g,h和k的另一个公共不动点,则由(1)可得

若 G(t,z,z)>0,则 (5)与 (φ1)矛盾,因此 G(t,z,z)=0,即 t=z.

综上可得，f,g,h和k有唯一的公共不动点.

定理 2.2设 h,k和 {fn}n∈Z+是 G-度量空间 (X,G)中的自映象,若映象对 (fn,h)和(fn+1,k)(∀n∈Z+)都是次相容的和相对连续的,则

(a)fn和h有重合点; (b)fn+1和k有重合点.

此外,如果∀x,y∈X,有以下不等式成立

则h,k和{fn}n∈Z+有唯一的公共不动点.

证明当n=1时,由定理2.1可得h,k,f1和f2有唯一的公共不动点,设为t.则t是h,k和f1的公共不动点,也是h,k和f2的公共不动点.下证唯一性,

假设h,k和f1有另外一个公共不动点z,且 t≠z,则由 (6)式有

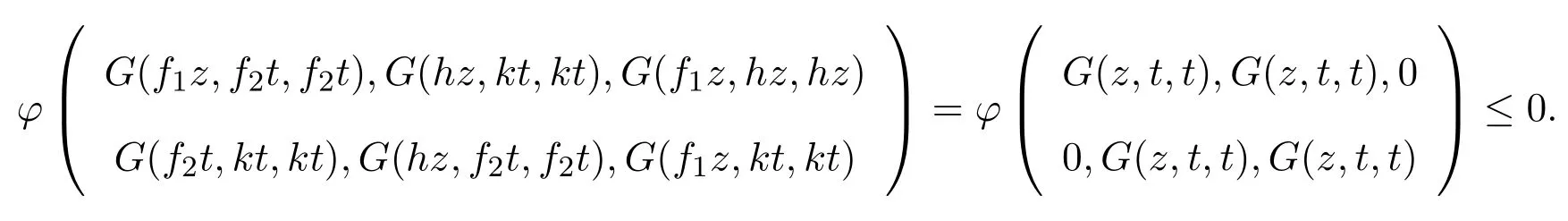
此结论与(φ1)矛盾,所以G(z,t,t)=0,即t=z.因此假设不成立,h,k和f1有唯一公共不动点.

同理可证h,k和f2有唯一公共不动点.

当n=2时,由定理2.1可得h,k,f2和f3有唯一的公共不动点,重复上面的方法可证得h,k和f3有唯一公共不动点.以此重复下去可证得h,k和{fn}n∈Z+有唯一的公共不动点.

定理 2.3令f,g,h和k是G-度量空间(X,G)中的四个自映象,若映象对(f,h)和(g,k)是次相容的和相对连续的,则

(a)f和h有重合点; (b)g和k有重合点.

此外,如果∀x,y∈X,有以下不等式成立

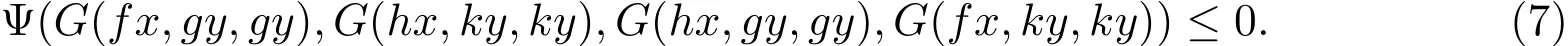
则f,g,h和k有唯一的公共不动点.

证明首先(a),(b)的证明与定理2.1相同,即存在{xn},{yn}⊂X,t,t′∈X,使得(2)式成立,并且 ft=ht,gt′=kt′. 现在证 t=t′. 使用 (7) 式可得

在上式中令n→∞,并注意到Ψ的下半连续性,可得

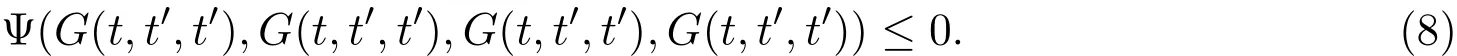
若 G(t,t′,t′)>0 则 (8) 式与 (Ψ1) 矛盾,因此 G(t,t′,t′)=0,即 t=t′.

再证ft=t.事实上,由(7)式可得

在上式中令n→∞,并注意到Ψ的下半连续性,ft=ht和t=t′,可得

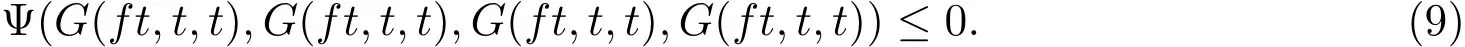
若 G(ft,t,t)>0,则 (9)式与 (Ψ1)矛盾,因此 G(ft,t,t)=0,即 ft=t.

同理可证gt=t.所以有

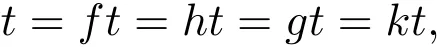
即t是映象f,g,h和k的公共不动点.

下证唯一性.假设f,g,h和k有另一个有公共不动点z,则由(7)式可得

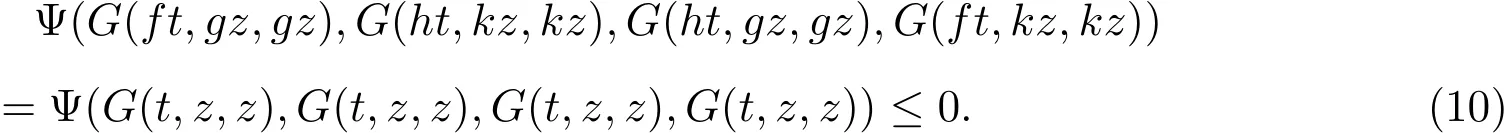
若 G(t,z,z)>0,则 (10)式与 (Ψ1)矛盾,因此 G(t,z,z)=0,即 t=z.

综上可得,f,g,h和k有唯一公共不动点.

定理 2.4令f,g,h和k是G-度量空间(X,G)中的四个自映象,若映象对(f,h)和(g,k)是次相容的和相对连续的,则

(a)f和h有重合点; (b)g和k有重合点.

此外,如果存在下半连续函数 Φ:[0,∞)→ [0,∞),满足 Φ(t)=0当且仅当 t=0,且∀x,y∈X,有

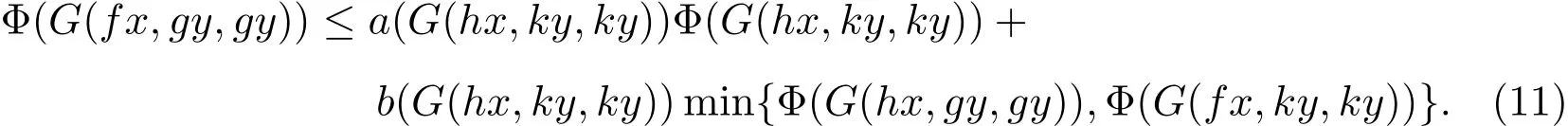
其中a,b:[0,∞)→[0,1)是两个下半连续函数,且满足条件

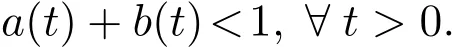
则f,g,h和k有唯一的公共不动点.

证明首先,与定理2.1相应部分的证明完全相同,可证存在{xn},{yn}⊂X,t,t′∈X,使得(2)式成立，并且

现在证 t=t′.否则,使用 (11)式可得

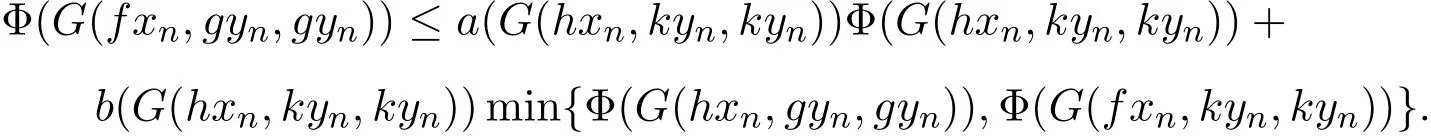
在上式中令n→∞,并使用函数Φ,a,和b的性质可得,

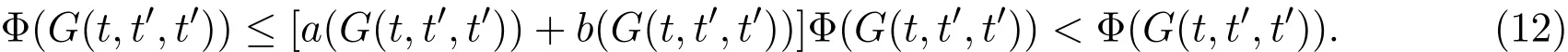
此为矛盾,所以 t=t′.

再证 ft=t,假设 ft≠t,则由 (11)式可得

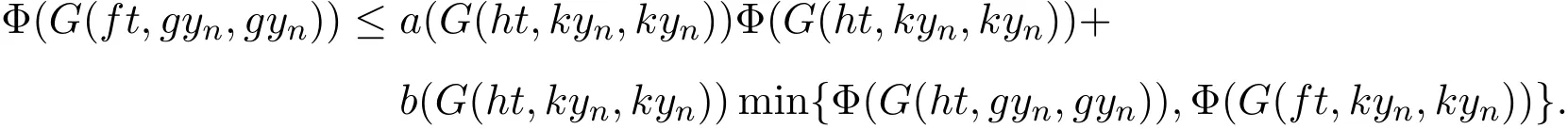
在上式中令n→∞,并考虑到函数Φ,a,和b的性质以及ft=ht,可得

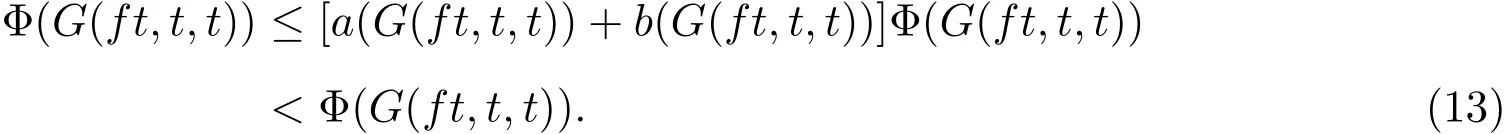
矛盾,故ft=t.

同理可证gt=t.所以有

即t是映象f,g,h和k的公共不动点.

下证唯一性.假设f,g,h和k有另一个公共不动点z,且t≠z,则G(t,z,z)>0.由(11)式可得

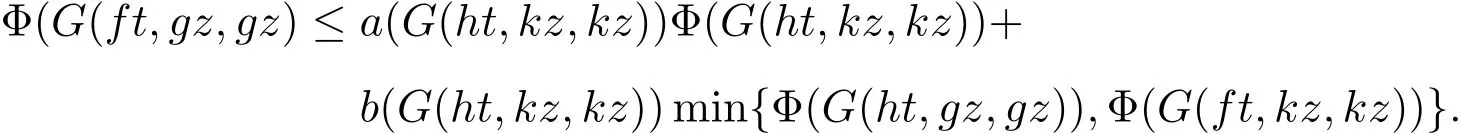
由t和z都是f,g,h和k的公共不动点,可得

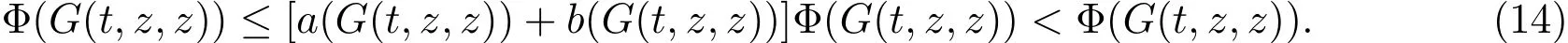
矛盾,所以t=z.

综上可得f,g,h和k有唯一的公共不动点.

注 2.1将定理2.4中的(11)式换成以下不等式,结论也是成立的.

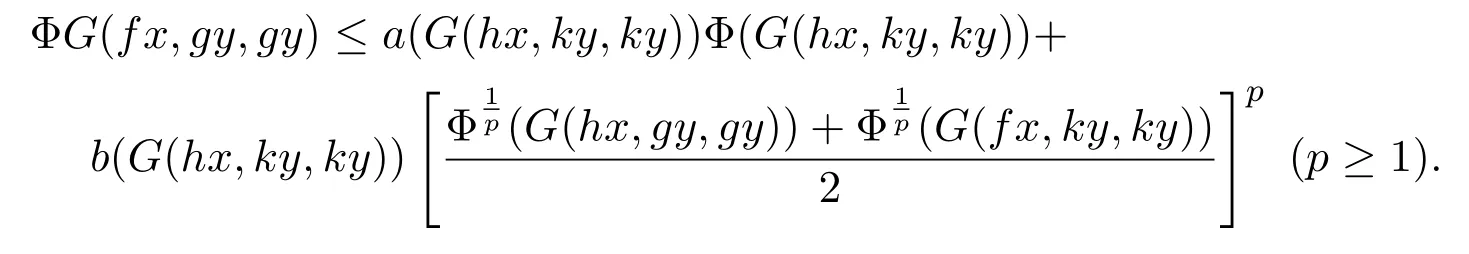
注 2.2在本文的所有定理和推论中,将条件中的次相容和相对连续分别换为相容和次序列连续,结论依然成立.

注 2.3在定理2.1、定理2.3和定理2.4中,如果取:

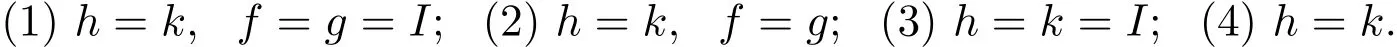
可以得到一些新的不动点和公共不动点定理,此处略去.

参考文献

[1]Mustafa Z,Sims B.A new approach to a generalized metric spaces[J].J.Nonlinear Convex Anal.,2006,7(2):289-297.

[2]Abbas M,Rhoades B E.Common fi xed point results for noncommuting mappings without continuity in generalized metric spaces[J].Appl.Mathe.Comput.,2009,215(1):262-269.

[3]Manro S,Bhatia S,Kumar S.Expansion mapping theorems in G-metric spaces[J].Int.J.Contemp.Math.Sciences,2010,5(51):2529-2535.

[4]Vats R K,Kumar S,Sihag V.Some common fi xed point theorems for compatible mappings of type(A)in complete G-metric spaces[J].Advances in Fuzzy Mathematics,2011,6(1):27-28.

[5]Popa V,Patricin A M.A general fi xed point theorem for pairs of weakly compatible mappings in G-metric spaces[J].J.Nonlinear Sci.Appl.,2012,5(2):151-160.

[6]Mustafa Z.Common fi xed points of weakly compatible mappings in G-metric spaces[J].Appl.Math.Sci.(Ruse),2012,6(89-92):4589-4600.

[7]Bouhadjera H,Godet-Thobie C.Common fi xed point theorems for pairs of subcompatible maps[J].17 June 2009.arXiv:0906.3159v1[math.FA].

[8]Imdad M,Ali J,Tanveer M.Remarks on some recent metrical common fi xed point theorems[J].Appl.Math.Lett.,2011,24(7):1165-1169.

[9]Pant P.A common fi xed point theorem under a new condition[J].Indian J.Pure Appl.Math.,1999,30(2):147-152.

Common fi xed point theorems for pairs of subcompatible maps in G-metric spaces

Zhang Qianwen,Gu Feng
(Department of Mathematics,Hangzhou Normal University,Hangzhou 310036,China)

In the framework of a G-metric spaces,we introduce notion of subcompatibility and reciprocally continuous,we prove some new fi xed point theorems using subcompatible and reciprocally continuous The results obtained in this paper extend and improve some well-known comparable results in the literature.

G-metric space,compatible,subcompatible,reciprocally continuous,subsequentially continuous,common fi xed point.

O177.91

A

1008-5513(2017)03-0298-09

10.3969/j.issn.1008-5513.2017.03.009

2017-03-31.

国家自然科学基金(11071169);浙江省自然科学基金(Y6110287).

张倩雯(1993-),硕士生,研究方向：应用非线性分析.

谷峰(1960-),教授,研究方向：应用非线性分析.

2010 MSC:47H10,54H25,55M20