线性模型中广义最小二乘参数估计误差分布的稳健性研究

熊琴

(广西大学数学与信息科学学院,广西 南宁 530004)

线性模型中广义最小二乘参数估计误差分布的稳健性研究

熊琴

(广西大学数学与信息科学学院,广西 南宁 530004)

研究了线性模型中广义最小二乘参数估计的误差分布稳健性问题.首先讨论了在线性统计模型里,设计矩阵为列降秩矩阵时,模型中给出了误差最大分布类,当误差向量的分布在此范围内变动时,LS估计和GLS估计在均方误差矩阵准则下是最优估计.然后进一步探讨广义最小二乘估计GLSE关于误差分布的稳健性,求出误差项所对应的最大分布族,进而证明了在该区间波动情况下,误差向量对应的始终为一致最优解.

线性模型;广义均方误差;稳健性;广义最小二乘估计;最佳线性无偏估计

1 引言

考虑线性模型Σ=y:

上式中y表示n×1阶观测向量,β表示p×1阶未知参数向量的具体数值,X 表示n×p阶矩阵情形,ε在上式中表示n×1随机误差向量,并且有rankX=r≤p.

在这里 φ(n)表示 n阶正定阵集合,n阶非负定阵集合用 φ(n)加以表示;A′表示 A的转置所生成向量空间,而R(A)则表示A的列向量生成的向量;N(A)w=为R(A)的正交补空间;Z在这里代表一个符合X′Z=0条件下的n×(n−r)阶列满秩矩阵.A+表示A的Moore-penrose逆,误差项ε的分布记为 P=h(ε),γ(u,V)表示期望u、协方差阵为δ2V 的分布族.其中

模型(1.1)中,当前已经有很多专家学者讨论了函数c′β的LS估计误差分布稳健性问题以及GLS估计误差分布稳健性问题[1-2].目前已经很多研究,在X 符合列满秩定义的情况下,文献[3-4]重点讨论了β最小二乘估计在实际应用中所具有积极意义,并对Gauss-Markov定理加以发展[5-7],从误差分布最大类角度对其进行创新.

随后,研究了当rank(X)=r≤p时,在均方误差矩阵准则下Xβ的LS估计

定义 1.1给定Xβ的估计类χ及误差项ε的一类分布γ(u,V),若δ∗∈χ,并且

对所有 δ∗∈ χ 及 P ∈ γ(u,V)都成立,则称 Xβ 的估计 δ∗是 [χ,γ(u,V)]最优.其中(δ,Xβ)为Xβ在γ上估计的广义均方误差数值,即:

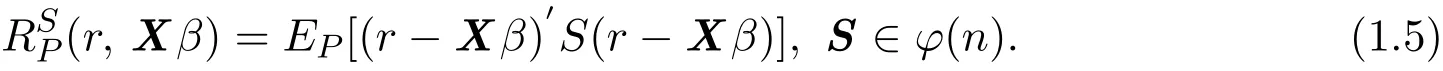
2 广义最小二乘估计的稳健性

本文中,对所构建模型 (1.1),在广义均方误差准则下研究函数 Xβ的广义最小二乘估计X(Σ)=X(X′Σ−1X)′X′Σ−1y的优良性.

给定的估计类:

当 P=h(ε)∈γ(0,Σ)时,χ为可估函数 Xβ的无偏估计类.在 P=h(ε)∈γ(u,Σ)条件满足情况下,可估函数Xβ的更广泛估计类这里我们用χ表示,其中涵盖有偏估计和无偏估计两大部分的内容.研究明确了误差项ε所对应的最大分布族γ(Σ),从而保证了在γ(Σ)区间波动情况下,ε对应的X(Σ)始终为[χ,γ(Σ)]最优.

引理 2.1设X 为n×p阶矩阵,Z满足X′Z=0且具有最大秩的矩阵,Σ∈φ(n),则有

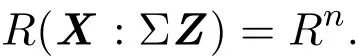
证明设任意 t∈R(X)∩R(ΣZ),存在 t1,t2,使得 t=Xt1= ΣZt2,利用 Z′X=0,Xt1=ΣZt2两边同时左乘Z′,得

由t的任意性,即得所要结论.

引理 2.3设 Eε=u,Cov(ε)=V,A 为 n 阶方阵,则有 E(ε′Aε)=u′Au+tr(AV).

3 主要结果

定理3.1若有P=h(ε)∈γ(u,V),那么常数Σ∈φ(n),X(Σ)对[χ,γ(Σ)]最优,其充分必要条件应有:

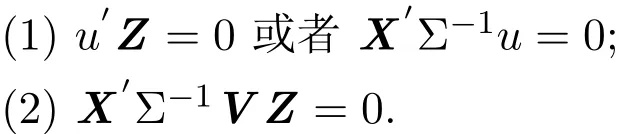
证明充分性.对任意P=h(ε)∈γ(u,V),当条件(1),(2)成立时,有Gu=0或Hu=0且 HVG′,其中

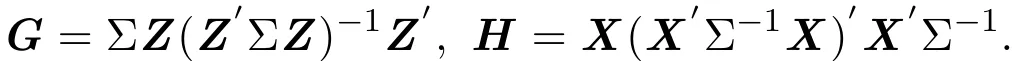
对任意 Ay∈χ,有AX=X,利用引理2.2,得

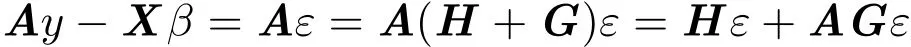
于是δ=Ay的广义均方误差:

由

从而

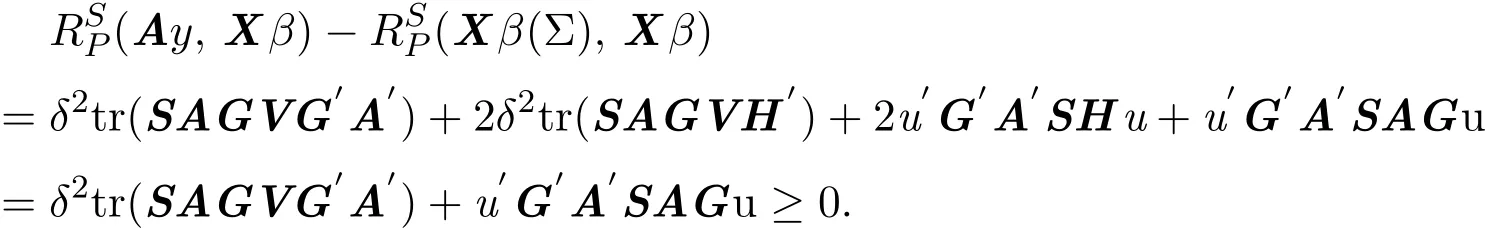
任意的δ2>0等价于

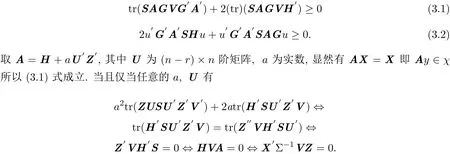
(3.2)式成立,当且仅当任意的a,U 有

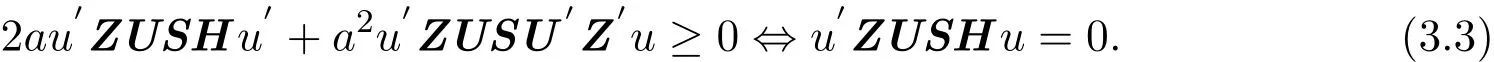
取 U=Z′uu′H′S−1,代入 (3.3)式,得:

定理 3.2给定估计类χ,令

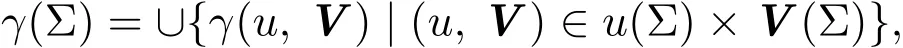
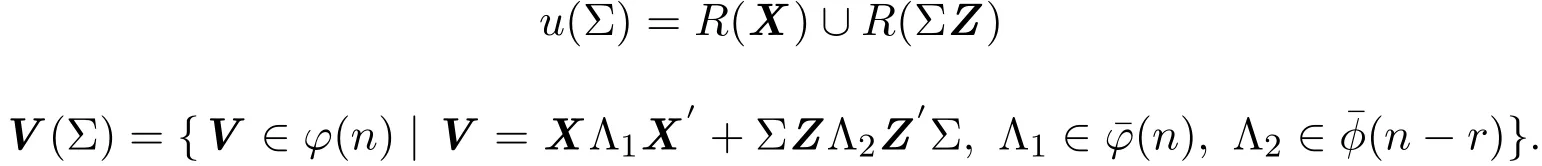
证明给定估计类χ,设X(Σ)是[χ,γ(Σ)]最优,则由定理3.1,有

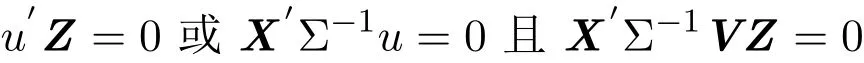
而 u′Z=0等价于 u∈R(X),X′Σ−1u等价于 u∈R(ΣZ),从而

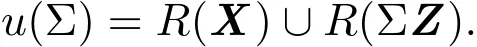
因 V ∈φ(n),则存在 n阶可逆矩阵Q,使得V=QQ′,不妨设Q=(X:ΣZ)M,记

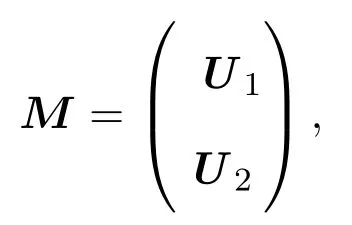
其中U1为p×n阶矩阵,U2为(n−r)×n阶矩阵,则

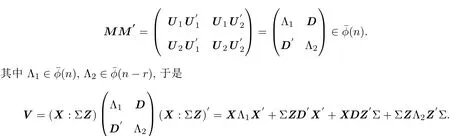
注意到 X′Z=0,有

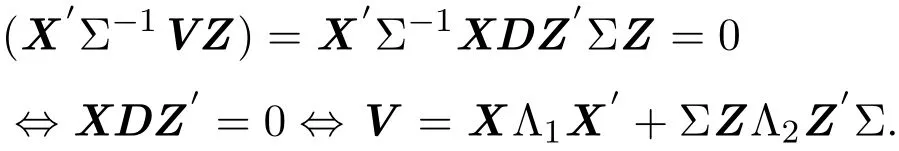
则γ(I)是使得Xβ的最小二乘估计

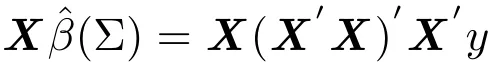
为χ,γ(I)最优的误差项ε的最大分布类,其中

参考文献

[1]邱红兵,罗季,孙旭.奇异线性模型下最小范数二次无偏估计关于误差分布的稳健性[J].华侨大学学报:自然版,2012,33(1):112-116.

[2]邱红兵.Bayes线性无偏估计关于误差协方差及先验分布的稳健性[J].广东工业大学学报,2016,33(5):5-8.

[3]Werner H J,Yapar C.A BLUE decomposition in the general linear regression model[J].Linear Algebra&Its Applications,1995,237-238:395-404.

[4]Kariya T,Kurata H.A Maximal Extension of the Gauss–Markov Theorem and Its Nonlinear Versions[M]//Generalized Least Squares.New York:John Wiley,2004:37-55.

[5]Jansen B J,Mullen T.Sponsored search:an overview of the concept,history,and technology[J].International Journal of Electronic Business,2008,6(2):114-131.

[6]邱红兵,罗季.Gauss-Markov估计关于误差分布的稳健性[J].应用概率统计,2010,26(6):615-622.

[7]胡桂开,彭萍.平衡损失下一般Gauss-Markov模型中回归系数的最优估计[J].应用概率统计,2015,31(2):113-124.

[8]朱万闯,林俊岐.基于格点搜索的随机效应的GLS估计[J].统计与信息论坛,2011,26(5):21-25.

[9]王松桂.线性模型的理论及其应用[M].合肥:安徽教育出版社,1987.

On robustness of GLSE in terms of error distributions in linear model

Xiong Qin
(Guangxi University,Academy of Mathematics and Information Sciences,Nanning 530004,China)

In this paper,we study the problem of robustness error distribution of generalized least squares estimation in linear model.First of all,we discuss LS estimation and GLS estimation in the mean square error matrix criterion is the optimal estimation.When the designed matrix is for the column rank matrix,the model gives the maximum error distribution,and the error vector distribution changes in the range.Then we conclude robustness of generalized estimation in term of error distribution in linear model.Calculate the error item corresponding to the maximum distribution,which proves that in the interval fl uctuations,the error vector corresponding to the optimal solution is always consistent.

linear model,the generalized mean square error,robustness,generalized linear estimation,the best linear unbiased estimation

O212.1

A

1008-5513(2017)03-0307-07

10.3969/j.issn.1008-5513.2017.03.0010

2017-03-27.

国家自然科学基金(71462002);广西自然科学基金(2013GXNSFAA019340).

熊琴(1982-),硕士生,研究方向:统计学.

2010 MSC:05A17