巧用平移求坐标

陈国玉

同学们若能灵活地运用点的平移规律。可以巧妙地求出点的坐标。

一、用点的平移规律

例1 已知点P的坐标为（3，-6），将点P先向左平移1个单位长度，再向上平移2个单位长度，得到点p，其坐标为____。

解析：点的坐标平移规律为“右加左减，上加下减”，即向右（或左）平移，横坐标要加（或减）平移的距离，纵坐标不变；向上（或下）平移，横坐标不变，纵坐标要加（或减）平移的距离。根据点的平移规律可知，向左平移1个单位长度，横坐标要减l，向上平移2个单位长度，纵坐标要加2。即3-1=2。-6+2=-4，所以点p的坐标为（2，-4）。

例2 在平面直角坐标系中，已知线段AB的两个端点分别是A（-4，-1），B（1，1）。将线段4B平移后得到线段AB，若点A的坐標为（-2，2），求点B的坐标。

解析：点A（-2，2）是由点A（-4，-1）先向右平移2个单位长度，再向上平移3个单位长度得到的，所以点B的平移方式为：先向右平移2个单位长度，再向上平移3个单位长度。根据点的平移规律可得，点B的坐标为（3，4）。

二、逆用点的平移规律

例3 将点M先向左平移2个单位长度，再向上平移1个单位长度得到M（-1，3）。求点M的坐标。

解析：将点M先向左平移2个单位长度，再向上平移1个单位长度得到M，反过来，将点M先向右平移2个单位长度，再向下平移1个单位长度得到点M，所以点M的坐标为（1，2）。

三、探究规律

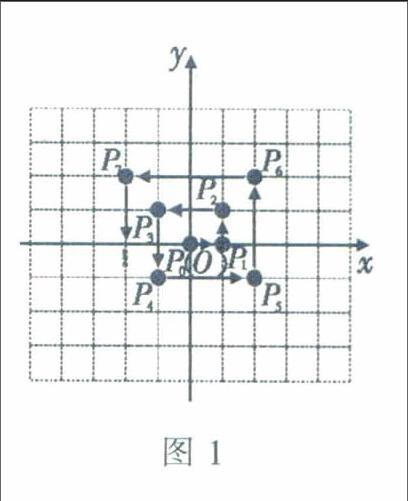
例4 一个点在平面直角坐标系中按下面的规律移动。如图1，从原点P₀（0，0）开始，先向右平移1个单位长度到点P₁，再向上平移1个单位长度到点P₂，再向左平移2个单位长度到点P₃，再向下平移2个单位长度到点P₄……按这个规律，点P₂₀₁₂的坐标为多少？

解析：根据图形可知：P₀（0，0）→P₁（1，0）→P₂（1，1）→P₃（-1，1）→P₄（-1，-1）→…，每移动四次为一组，横坐标和纵坐标都减少1。

点P₂₀₁₂是移动2 012次得到的，可以分为503组，所以横坐标减少503，纵坐标减少503，即点P₂₀₁₂的坐标为（-503，-503）。

责任编辑：胡云志