蜘蛛网诱发的数学革命

2017-07-08孔凡哲祖丹

中学生数理化·七年级数学人教版 2017年4期

孔凡哲　祖丹

在人类发展史上相当长的时间内，代数问题只能通过代数方法加以解决。而几何问题也只能通过几何工具加以解决。正是由于一位伟大数学家笛卡儿一次偶然的发明。开启了人类数学的新天地——这就是建立坐标系、形成解析法。有了解析法这个非常重要的数学工具。代数学与几何学之间的壁垒被彻底打破。一门新的学科——解析几何诞生了。

一、偶然中的必然

据说，正服兵役的法国哲学家、数学家笛卡儿。在一次战斗中被俘，被关进牢房。每天孤独的时光无法打发，只有墙角上的那个蜘蛛网能给他带来一丝快乐。他惊奇地发现。蹲在蜘蛛网中心的蜘蛛，总能准确无误地捕捉到撞到蜘蛛网上的蚊子、苍蝇等猎物（如图1所示）。为什么呢？

笛卡儿发现，埋伏在蜘蛛网中心的蜘蛛，能通过究竟是哪根蜘蛛网线震动，以及震动的强度。判断猎物在哪个方位和距离中心有多远。

这意味着。在蜘蛛网上。确定一个点的位置。需要而且仅仅需要两个量即可。

受蜘蛛捕捉猎物的启发，笛卡儿发明了一种确定位置的有效工具——平面直角坐标系。他的方法是：

在平面内，画两条原点重合、相互垂直而且具有相同单位长度的数轴。这样就建立了平面直角坐标系。

有了这个伟大的发明，人们就可用一对有序实数表示平面内的点的位置。为了纪念笛卡儿这个重大贡献。人们通常将平面直角坐标系称为笛卡儿坐标系，将这种方法称为解析法。

二、感受确定位置的多种方法。培养空间观念

生活中经常需要确定物体的位置。比如，确定学校的位置，对弈时确定棋子的位置。海战中确定舰艇的位置等。在平面内确定物体的位置，一个数据肯定是不够的。比如。在电影院找座位。不仅需要知道第几排。还需要知道第几个座位。

利用方位角和距离，可以确定物体的位置。蜘蛛就是如此。一只蜘蛛想要抓住粘在蜘蛛网上的猎物，在实施抓捕前，它必须确定两个数据：一个是猎物到自己的距离，另一个是猎物相对于自己的方位角。

与蜘蛛相似。炮兵对目标进行射击时。需要确定方位角和距离。如下页图2所示。此时，炮兵就是凭借距离和方位角两个数据对敌方阵地进行精准射击的。

同样地，我们可以用经度和纬度确定位置。例如，2016年11月18日下午。总飞行时间长达33天的神舟十一号载人飞船顺利返回着陆。人们利用“全球定位系统”——GPS，在茫茫草原上，很快找到了着陆的返回舱（如图3所示）。这是因为全球任何一个地方都存在唯一的经度和纬度，可以通过目标物（如神舟十一号飞船的返回舱）发出的信号，利用GPS测得它所在位置的经度和纬度，就能顺利找到返回舱。

虽然用来确定平面位置的方法多种多样，但是，它们都有一个共同的特征，这就是需要两个基本数据。亦即，在平面内，确定点的位置需要两个（彼此独立的）数据。

三、积累几何经验，进一步发展数形结合意识

在生活中。平面直角坐标系最重要的作用就是利用有序数对定位。

在象棋中，马3进4（第三列的马进到第四列）和马4进3（第四列的马进到第三列）中的3代表的含义是完全不同的。

在平面直角坐标系中，对于平面上的任意一点P，都有唯一的一个有序数对（a，b）与它对应；反过来，对于任意一个有序数对（a，b），都有平面上唯一的一点P与它对应。

下面是一道密码题。如图4。有两组有序数对（2，5）（1，3）（4，6）（1，6）和（5，2）（3，1）（6，4）（6，1），你能根據这两组有序数对分别找到所对应的成语吗？[注：（2，5）对应的汉字是“天”]

那么，成语“破釜沉舟”对应的密码是什么？你还能找到哪些成语？请写出它们的密码。

四、中考通关

例题（2016年呼和浩特）已知平行四边形ABCD的顶点A在第三象限。对角线AC的中点为坐标原点，一边AB与戈轴平行且AB=2。若点A的坐标为（a，b），则点D的坐标为____。

分析：这道题考查的是平行四边形的性质，用有序数对表示点的位置，坐标图形变换（对称）等知识，难度较大。根据平行四边形的性质得到CD=AB=2。由已知条件得到点B的坐标为（2+a，b）或（a-2，6），再根据点D与点B关于原点对称。即可得到结论。

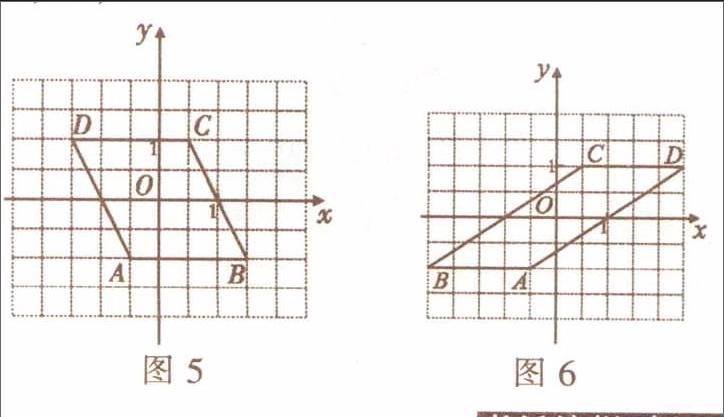
解：如图5所示。

∵四边形ABCD是平行四边形。