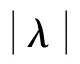高压下一维双原子链中杂质引起的反对称局域振动模

吕岿，毛杰键，刘云霞

(上饶师范学院 物理与电子信息学院，江西 上饶 334001)



高压下一维双原子链中杂质引起的反对称局域振动模

吕岿，毛杰键，刘云霞

(上饶师范学院 物理与电子信息学院，江西 上饶 334001)

考虑了原子间次近邻相互作用，讨论了高压下一维双原子链中杂质引起的局域振动，得到次近邻作用常数对反对称局域模的振动频率及局域程度的影响的基本特征。

杂质；次近邻作用；局域模

对于一维双原子链中杂质引起的局域振动，人们已做了大量的研究工作[1-4]，然而这些工作一般采用最近邻近似，未涉及原子间次近邻互作用力的影响。在高压条件下, 由于原子间距的缩小，每一原子与其近邻原子的电子云将发生重叠变化，不仅两个原子间，更多个原子间将同时存在相互作用[5-6]。那么，高压下考虑原子间次近邻相互作用，对杂质引起的局域振动有没有影响，如果有，影响如何? 本文将对这一问题进行讨论。

1 理论模型

设一维双原子链中基质原子质量分别为m1与m2，相邻原子间的平衡距离为a，原胞大小为2a。质量为M的杂质替代链中质量为m2的原子。取杂质所在位置为坐标原点，以u2n表示第n个原胞内质量为m2的原子离开平衡位置的位移, 以u2n-1表示第n个原胞内质量为m1的原子离开平衡位置的位移,其中n=±1，±2，…，±N.

在简谐近似下,考虑最近邻及次近邻作用的一维双原子链晶格振动的拉格朗日函数为:

(1)

式中α、β分别是基质原子间的最近邻、次近邻力常数，α′、β′分别是杂质与基质原子间的最近邻、次近邻力常数。应用拉格朗日方程，可得到相应的晶格振动运动方程组为：

(2)

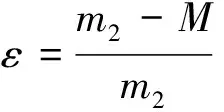
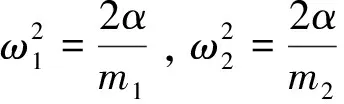
(3)

2 振动方程组的反对称局域模

由于杂质左右两端的半无限链对杂质具有反演对称性，符合这一要求的解具有反对称和对称两种可能的性质，本文仅对其中反对称局域振动情况进行讨论。

(4)

3 结果与讨论

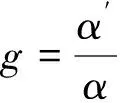
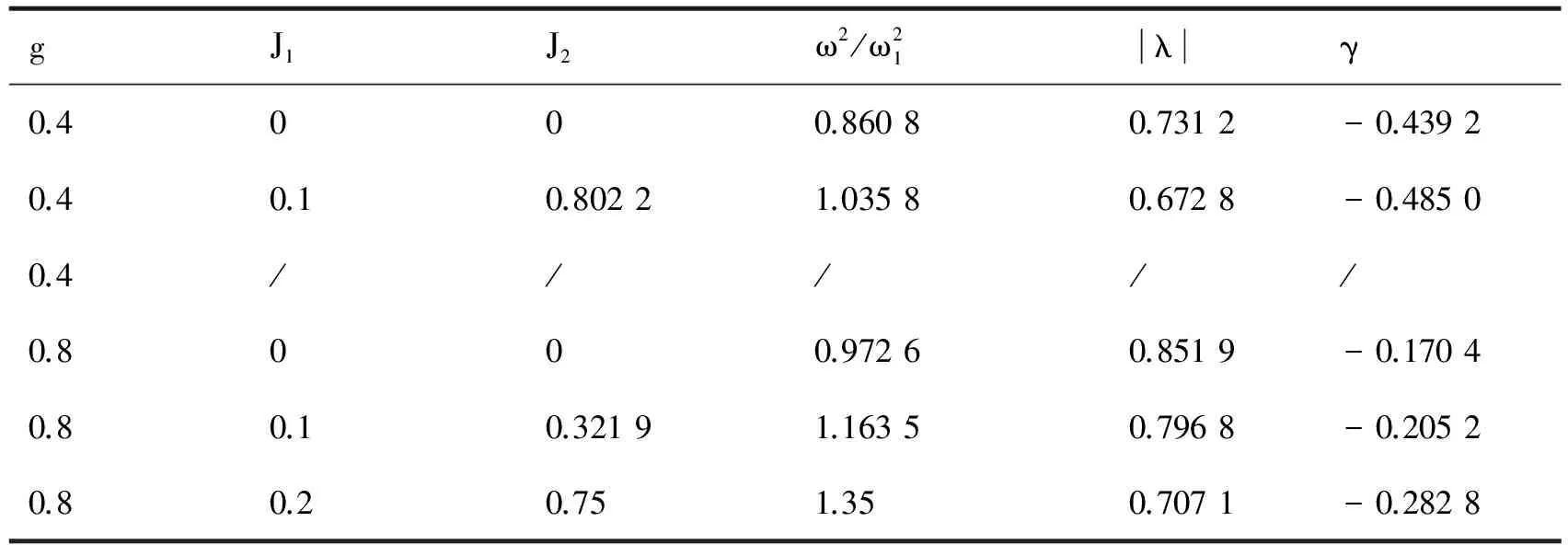
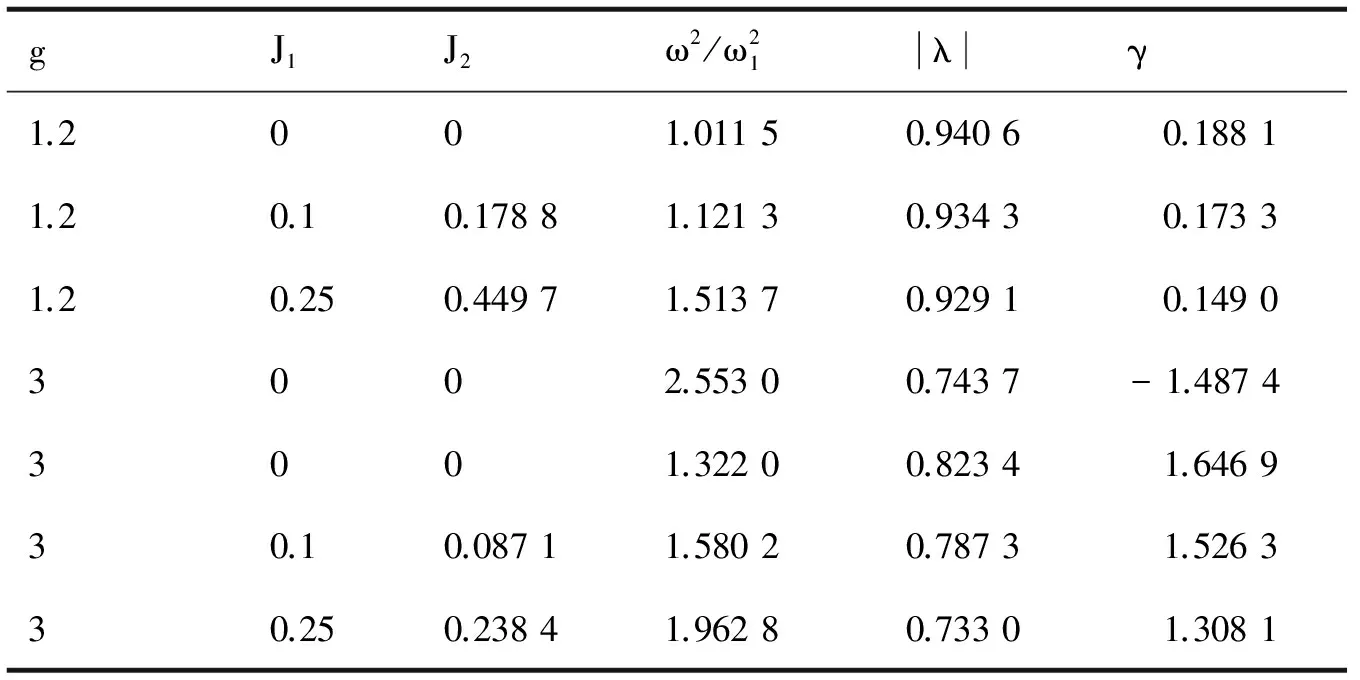
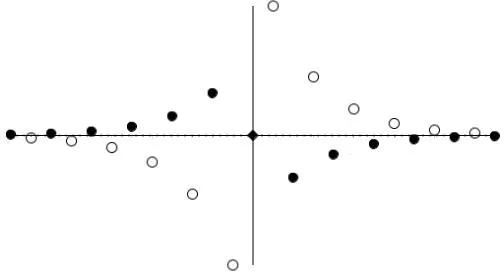
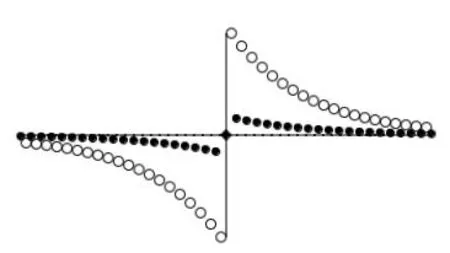
对于杂质原子取代小原子即k>1的情况，若不考虑次近邻作用，则g>1时产生局域模[4]；若次近邻作用不等于零(J1≠0，J2≠0)，则g>1且较小时,J2>J1才产生局域模，而g>1且较大时,J2

图1、图2则分别给出了杂质替代链中基质大原子、小原子时的实空间图像。

表1 杂质原子取代基质大原子(k=0.5)时的反对称局域模

表2 杂质原子取代基质小原子(k=1.5)时的反对称局域模

图1 杂质替代大原子时(k=0.5,g=0.4,J1=0.1)反对称局域模的实空间图像，具光学支模特征

图2 杂质替代小原子时(k=1.5,g=1.2,J1=0.1)反对称局域模的实空间图像，具声学支模特征

k，g，J1，J2取其它值时，情况与上述分析类似。

综上所述，在高压条件下，考虑到一维双原子链原子间的次近邻作用，杂质引起的反对称局域模频率升高，局域性变好，但产生局域模的条件比只考虑最近邻作用时更为严格，即只有J1，J2的大小关系恰当时才能产生反对称局域振动。如同时考虑第三、第四近邻等多原子间互作用力的影响，情况会更为复杂，对此我们将另文讨论。

[1] 高英俊.杂质引起的双原子链晶格振动频率的变化[J].广西大学学报(自然科学版),1994,19(3):327-331.

[2] 许小亮,施朝淑.GaN中的缺陷与杂质[J].物理学进展,2001,21(1):1-11.

[3] 张启义,祝亚,田强.一维双原子链中杂质引起的局域振动模[J].大学物理,2004,23(11):12-14,16.

[4] 吕岿,童国平,毛杰键．具有在位势的一维双原子链中杂质引起的局域振动[J]．原子与分子物理学报,2012,39(1):157-162.

[5] 田春玲,刘福生,蔡灵仓,等.多体相互作用对高压固氦状态方程的影响[J].物理学报,2006,55(2):754-769.

[6] 李金星,张道华,朱国良,等.考虑次近邻作用原子链的热传导研究[J].湖北师范学院学报(自然科学版),2014,34(4):7-11.

The Local Anti-symmetric Vibration Mode Induced by An Impurity Atom in A Diatomic Linear Chain under the High-pressure Condition

LV Kui, MAO Jiejian, LIU Yunxia

(School of Physics and Electronic Information,Shangrao Normal University, Shangrao Jiangxi 334001,China)

Considering the next- nearest- neighbor interaction between the atoms under the high-pressure condition, the lattice vibration equation of a diatomic chain with an impurity are solved, and the basic feature of the effect of the next-nearest-neighbor interaction on the anti-symmetric vibration are given.

impurity; next-nearest-neighbor interaction; local vibration

2017-03-30

吕岿(1970-),男,江西横峰人,副教授,硕士,主要从事理论物理教学与研究。E-mail: 363036787@qq.com

O481

A

1004-2237(2017)03-0054-04

10.3969/j.issn.1004-2237.2017.03.011