与热库耦合的光学腔内三原子间的纠缠动力学∗

邢贵超 夏云杰

(曲阜师范大学物理工程学院,山东省激光偏光与信息技术重点实验室,曲阜 273165)

1 引 言

量子纠缠[1,2]是量子力学最显著的特征之一,是量子信息理论[3]的重要课题.它在量子隐形传态、量子密集编码、量子纠错、量子密钥分配和量子计算等[4−10]方面发挥着重要作用.近几年,量子纠缠在量子信息处理中发挥着越来越重要的作用,从而引起了人们更加广泛的关注.然而,由于实际系统不可避免地会与周围环境发生相互作用,进而导致纠缠随时间不断衰减,甚至在有限时间内完全消失,即出现纠缠突然死亡(ESD)[11,12].近年来,人们开始从不同的角度探讨如何来保护纠缠.例如,宗晓岚等[13]利用弱测量和反转测量的方法来保护多粒子的纠缠.因此,了解开放量子系统在各种环境下的动力学性质,并通过优化耦合参量来对系统进行调控具有重要意义.

对开放量子系统动力学,特别是针对零温环境的研究有了较为成熟的方法[14].到目前为止,人们从独立环境和共同环境两个角度分别研究了原子间的纠缠演化特性.例如,Yu和Eberly[15]研究了两个相互纠缠的二能级原子分别与不同的腔作用出现了纠缠死亡的现象;Wu和Zhang[16]研究了分别囚禁在被Kerr介质填充的腔中的两个二能级原子间的纠缠特性.但是,由于多体纠缠度本身的复杂性和不完善性,多体纠缠的研究在某些方面受到了限制.最近,Bai等[17,18]研究了多个量子比特分别与各自独立的腔作用的纠缠动力学.对于共同环境,Maniscalco等[19]研究了两个原子与同一环境作用的纠缠动力学以及通过量子芝诺效应保护纠缠.Bellomo等[20]研究发现纠缠在有限时间内死亡后会出现纠缠复苏的现象,这是因为非马尔科夫热库具有记忆效应.贺志和李龙武[21]通过精确求解带有偶极-偶极相互作用的两个二能级原子与一个共同热库相互作用模型,得到了两原子间量子纠缠和量子失谐的解析表达式.相对于二体系统,三体或多体系统的纠缠更加复杂.例如,Ma等[22−24]研究了对于不同的共同环境中的三原子的纠缠动力学.封玲娟和夏云杰[25]研究了三个二能级原子与共同热库发生相互作用的系统纠缠动力学演化.

最近,文献[26,27]分别研究了有热库耦合的光学腔内两个相互作用的二能级原子间的纠缠动力学以及系统马尔科夫和非马尔科夫动力学的转换,但是对于更复杂体系的研究尚未完善.基于此,本文研究了有热库耦合的光学腔内三个相互作用的二能级原子间的纠缠动力学和系统的纠缠转移.

2 理论模型

考虑三个全同的相互作用的二能级原子A,B,C(为了处理的方便,我们假设三原子两两相互作用强度均为D,实验上可以由三个原子在光学腔中形成等腰三角形结构来实现)与一个同零温玻色库耦合的光学腔相互作用,假设原子间距离小于腔场波长,使得原子间偶极-偶极相互作用不可忽略.系统的总哈密顿量可以写成:

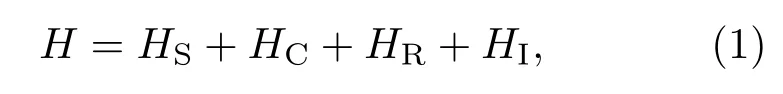
其中,ω0, ωc和ωk分别为原子的跃迁频率、腔场的本征频率和热库的第k个模式的频率;和分别为第i(i=1,2,3)个原子的赝自旋算符分别为原子的激发态和基态);a和a+分别为光子的淹没和产生算符,bk和分别为热库第k个模式的淹没和产生算符;D,κ和gk分别为原子间偶极-偶极相互作用强度、原子与腔场耦合强度和腔与热库第k个模式的耦合强度.为方便,令ω0=ωc.

假设三原子A,B,C初始处于W型纠缠态,初始时刻腔场和热库均处于真空态,则整个体系的初态可表示如下:

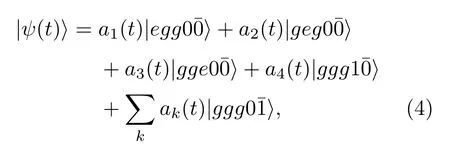
将(4)式代入相互作用绘景中的薛定谔方程

可以得到关于演化系数的微分方程组:

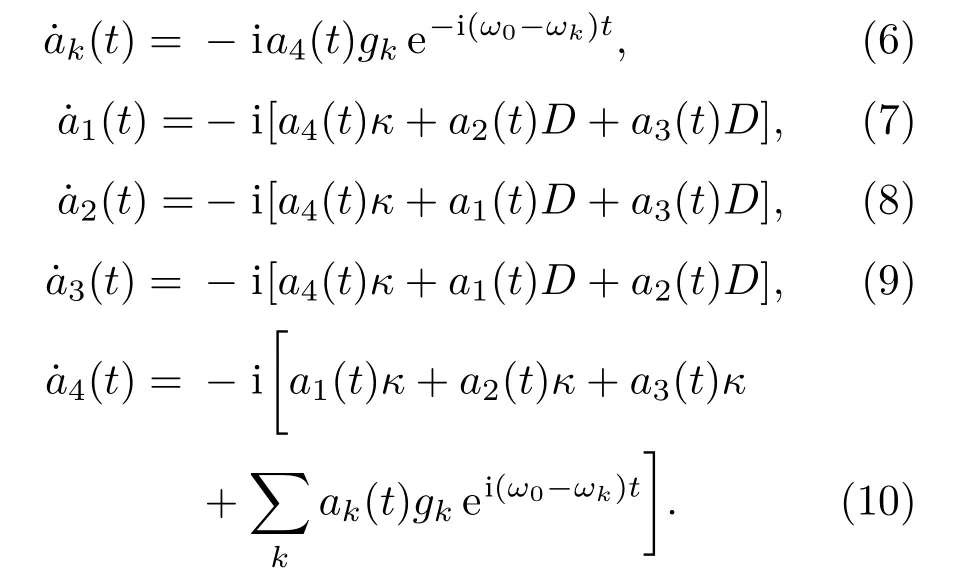
考虑ak(0)=0对(6)式进行积分得:

将(11)式代入(10)式得:

其中,参数γ ,λ ,∆分别代表腔场与热库的耦合强度、热库的谱宽度和腔场与热库的失谐量.当λ>2γ时,腔场与热库之间为弱耦合,反之,为强耦合.通过引入关联函数f(t−t′)来定义下面关于热库谱密度J(ω)的傅里叶变换:

(12)式可以重新写为

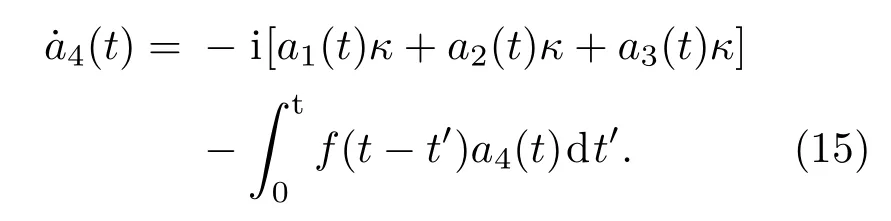
对(7),(8),(9)式以及(15)式进行拉普拉斯变换,得:

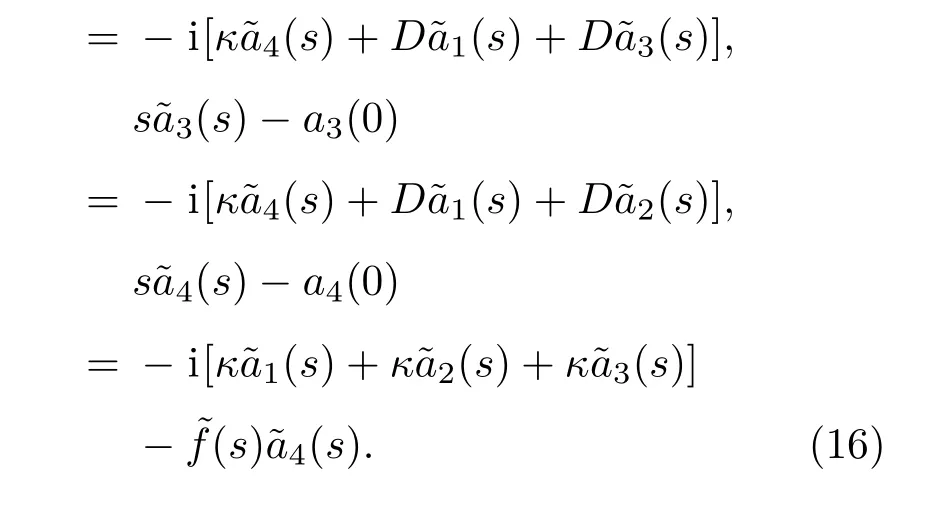
3 数值计算与理论分析

利用下限共生(LBC)和共生纠缠(concurrence)方法分别度量三原子间纠缠以及腔场和热库间的纠缠.

利用(4)式对三原子求迹得腔场与热库的约化密度矩阵在基矢下表示为

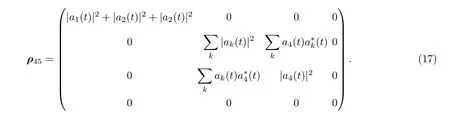
对于两体纠缠度量, 基矢空间为{|00〉,|01〉,|10〉,|11〉}的X型量子态密度矩阵为

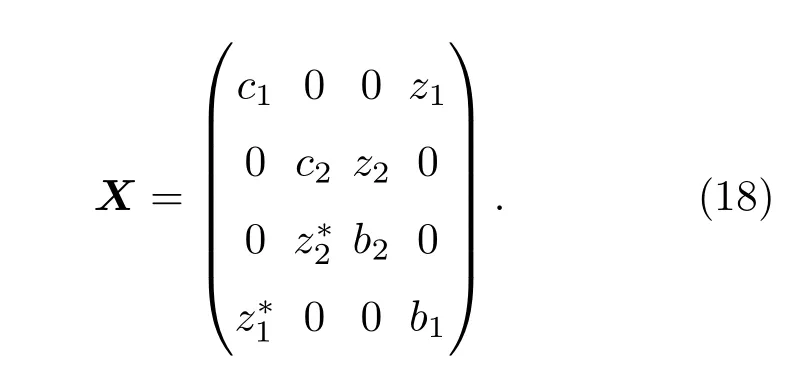
它们可以用Wootters提出的共生纠缠(concurrence)[28]来度量:

根据共生纠缠得到腔与热库的纠缠度为

对于三量子比特的纠缠度量,通常有文献[29]提出的LBC和文献[30]提出的三体部分转置负本征值等方法.本文采用下限共生方法,其表示如下[31]:

其中,

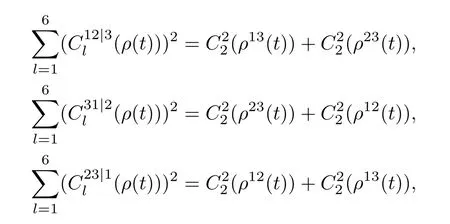
对(23)式和(20)式做数值计算,可得三原子纠缠以及腔场与热库间纠缠随时间t的演化规律如图1—图4所示.比较图像可以看出系统的纠缠动力学.

4 不同耦合参数对系统纠缠的影响

4.1 原子间耦合强度对系统纠缠的影响

图1(a)和图1(b)分别描述原子与腔场耦合强度κ一定时,腔场与热库弱耦合情况下,对于不同的原子间耦合强度,原子之间纠缠以及腔场与热库间纠缠随时间的演化.由图可以看出,一定时间内原子之间的耦合强度越强,原子间纠缠越大、腔场与热库间的纠缠越小.出现此现象的原因是原子量子态由态跃迁到态时产生光子,当D=0和D=0.1γ时,原子间相互作用相比于原子与腔场的相互作用较小,所产生的光子被腔场吸收的概率大于原子量子态由态跃迁到态时光子被吸收的概率,所以减小(n=1,2,3),由(23)式原子间纠缠度C3的表达式可知,原子间纠缠也减小,且一定时间内呈现单调递减的趋势.随着原子间的相互作用增强,原子跃迁得到光子的概率变大,腔场得到光子的概率变小,相应三原子间的纠缠度变大,腔场与热库间的纠缠变小.当D=γ时,原子间相互作用相比于原子与腔场间的相互作用较大,所产生的光子被腔场吸收的概率小于原子量子态由态跃迁到态时光子被吸收的概率.随时间的演化,光子不断地产生,不断地被吸收,此过程不断循环发生.但由于腔场与环境的相互作用会导致光子的泄露,所以重吸收光子的概率逐次递减直至消失,表现为图像呈现振荡衰减趋势.通过数值计算,当时间趋于无穷大时3),所以原子间纠缠最终趋于一不为零的稳定值.对比图1(c),可以看出腔场与热库强耦合时与弱耦合时三原子间有相似的纠缠动力学行为.

图1 腔场与热库弱耦合情况下,对于不同的原子间耦合强度D,(a)三原子间的纠缠随时间t的演化,(b)腔场与热库间的纠缠随时间t的演化,参数5γ,κ=0.1γ,∆=0,γ=1;(c)腔场与热库强耦合情况下,对于不同的D三原子间的纠缠随时间t的演化,参数λ=0.2γ,κ=0.1γ,∆=0,γ=1Fig.1.(a)The entanglement of three atoms as a function of scaled time t,(b)the entanglement of cavity and reservoir as a function of scaled time t for a weak coupling regime between the cavity and reservoir and different dipole-dipole interaction strength D,param-etersλ=5γ,κ=0.1γ,∆=0,γ=1,(c)the entanglement of three atoms as a function of scaled time t for a strong coupling regime between the cav-ity and reservoir and di ff erent dipole-dipole interac-tion strength D,parametersλ=0.2γ,κ=0.1γ,∆=0,γ=1.

4.2 原子与腔场耦合强度对系统纠缠的影响

图2(a)和图2(b)分别描述的是在原子间不存在偶极-偶极相互作用,腔场与热库弱耦合情况下,对于不同的原子与腔场间耦合强度κ,三原子间的纠缠以及腔场与热库间的纠缠随时间t的演化.由图可看出,在短时间内,原子间纠缠随着原子与腔耦合强度的增加而减小,在长时极限下趋于稳定值.κ较大时,三原子间的纠缠随时间t的演化出现明显的周期性振荡衰减行为.腔场与热库强耦合时,会出现相似的纠缠动力学行为.腔场与热库间纠缠由零增大到一定值后最终减小为零,腔与库之间的纠缠在短时间内随原子与腔的耦合强度的增加而增加,当原子与腔场耦合强度较强时会出现振荡.由图可知,当κ=0.1γ和κ=0.2γ时,原子与腔场间耦合较弱,由图像可以看出纠缠没有出现振荡衰减现象,说明流入环境的信息没有重新流回原子系统,即纠缠在演化过程中出现马尔科夫效应.当κ=2γ时,由图可以看出纠缠出现振荡衰减的现象,也就是流入环境的信息在系统演化过程中重新流回原子系统,从而导致原子间纠缠出现了非马尔科夫效应.

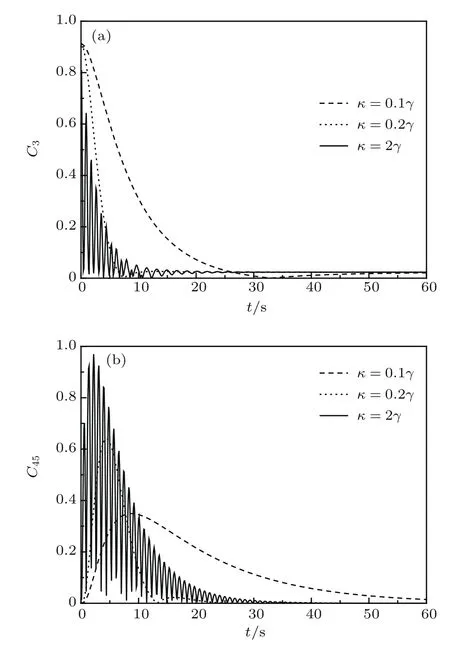
图2 腔场与热库弱耦合情况下,对于不同的原子与腔场耦合强度κ,三原子间的纠缠(a);腔场与热库间的纠缠(b)随时间t的演化;参数:=5γ,D=0,∆=0,γ=1Fig.2.(a)The entanglement of three atoms as a function of scaled time t;(b)the entanglement of cavity and reservoir as a function of scaled time t for a weak coupling regime between cavity and reservoir and di ff erent coupling strength κ.Parameters:=5γ,D=0,∆=0,γ=1.

4.3 热库谱宽对原子间纠缠以及非马尔科夫性的影响

当λ<2γ时,热库与腔场为强耦合,原子与腔场组成的系统遵循非马尔科夫动力学.由图可以看出,λ=0.5γ时,纠缠突然死亡后出现了复苏,说明从环境到原子系统有了信息的回流,表现出非马尔科夫效应.λ=γ时,此时原子与腔场组成的系统虽然遵循非马尔科夫动力学,但由图像可以看出,原子间纠缠单调递减,没有和外部环境的信息交流,表现出马尔科夫效应.随着λ增加,当λ=5γ以及λ=100γ时,热库和腔场为弱耦合,系统遵循马尔科夫动力学,但从原子系统到环境出现了信息的交流,表现出非马尔科夫效应.结合3.2节可以看出体系的非马尔科夫效应由参数κ和λ共同决定.

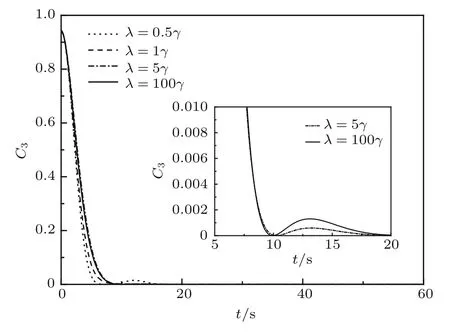
图3 当系统初始态为最大纠缠态,对于不同的热库谱宽λ,三原子间的纠缠随时间t的演化0.3γ,D=0,∆=0,γ=1)Fig.3.The entanglement of three atoms as a function of scaled time t for di ff erent λ when the initial state is the maximally entangled state parameters:κ=0.3γ,D=0,∆=0,γ=1.

4.4 腔场与热库失谐对系统纠缠的影响

图4(a)和图4(b)分别给出了在腔场与热库耦合强度较弱和较强时原子间纠缠在不同失谐情况下随时间t的演化.可以看出当腔场与热库耦合强度较弱时,三原子间纠缠随失谐量的增加而增加,但不是特别明显,最终在长时极限下趋于一稳定值.当腔场与热库耦合强度较强时,随失谐量的增大,原子间纠缠增加,呈现周期性振荡.由于失谐可以抑制从原子到腔场以及热库间的纠缠转移,因此失谐可以抑制热库耗散对原子间纠缠衰减的影响,使得原子间纠缠增强而腔与热库间纠缠减弱.因此,调整失谐可以加强对原子间纠缠的利用.

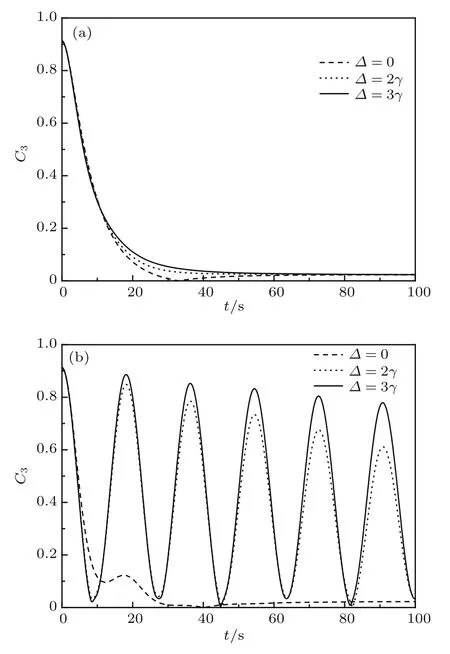
图4 对于不同的失谐量∆,三原子间纠缠随时间t的演化 (a)腔场与热库弱耦合的情况下,0.1γ,D=0,λ=5γ,γ=1;(b)腔场与热库强耦合的情况下,κ=0.1γ,D=0,λ=0.2γ,γ=1Fig.4.The entanglement of three atoms as a function of scaled time t for di ff erent values of detuning in terms of∆:(a)Under weak co upling regimes between the cavity and reservoir,κ=0.1γ,D=0,λ=5γ,γ=1;(b)under strong co upling regimes between the cavity and reservoir,κ=0.1γ,D=0,λ=0.2γ,γ=1.

5 结 论

本文以三个相互作用的二能级原子与一个同零温玻色库耦合的光学腔相互作用为模型,研究腔内三个原子之间以及腔与热库之间的纠缠动力学.分别研究了原子间耦合强度、原子与腔耦合强度、热库谱宽度以及腔场和热库的失谐量对原子间以及腔场与热库间纠缠动力学的影响.研究发现:原子间纠缠随着原子间耦合强度的增加而增加,随原子与腔场间耦合强度的增加而减小;体系的非马尔科夫性由参数κ和λ共同决定;调整腔场与热库的失谐可以有效抑制热库耗散对纠缠衰减的影响.

[1]Horodedecki R,Horodedeck P,Horodedecki M,Horodedecki K 2009Rev.Mod.Phys.81 865

[2]Zyczkowski K,Horodedecki P,Horodedecki M,Horodedecki R 2001Phys.Rev.A65 012101

[3]Zhang Y D 2012Principles of Quantum Information Physics(Beijing:Science Press)pp258–307(in Chinese)[张永德2012量子信息物理原理(第一版)(北京:科学出版社)第258—307页]

[4]Bennett C H,Brassard G,Crépeau C,Jozsa R,Peres A,Wootters W K 1993Phys.Rev.Lett.70 1895

[5]Hillery M,Bužek V,Berthiaume A 1999Phys.Rev.A59 1892

[6]Ekert A K 1991Phys.Rev.Lett.67 661

[7]Yan L H,Gao Y F,Zhao J G 2009Int.J.Theor.Phys.48 2445

[8]Murao M,Vedral V 2001Phys.Rev.Lett.86 352

[9]Deng F G,Ren B C,Li X H 2017Sci.Bull.62 44

[10]Sheng Y B,Zhou L 2017Sci.Bull.62 1025

[11]Yu T,Eberly J H 2006Phys.Rev.Lett.97 140403

[12]Almeida M P,de Melo F,Hor-Meyll M,Salles A,Walborn S P,Souto Ribeiro P H,Davidovich L 2007Science316 579

[13]Zong X L,Yang M 2016Acta Phys.Sin.65 080303(in Chinese)[宗晓岚,杨名 2016物理学报 65 080303]

[14]Breuer H P,Petruccione F 2002Theory of Oopen Qquantum Systems(Oxford:Oxford University Press)pp568–617

[15]Yu T,Eberly J H 2004Phys.Rev.Lett.93 140404

[16]Wu Q,Zhang Z M 2014Chin.Phys.B23 034203

[17]Bai Y K,Ye M Y,Wang Z D 2009Phys.Rev.A80 044301

[18]Bai Y K,Xu Y F,Wang Z D 2014Phys.Rev.Lett.113 100503

[19]Maniscalco S,Francica F,Zaffino R L,Gullo N L,Plastina F 2008Phys.Rev.Lett.100 090503

[20]Bellomo B,Lo Franco R,Compagno G 2008Phys.Rev.A77 032342

[21]He Z,Li L W 2013Acta Phys.Sin.62 180301(in Chinese)[贺志,李龙武 2013物理学报 62 180301]

[22]Ma X S,Wang A M,Yang X D,You H 2005J.Phys.A38 2761

[23]Ma X S,Wang A M,Cao Y 2007Phys.Rev.B76 155327

[24]Ma X S,Liu G S,Wang A M 2011Int.J.Quant.Inf.9 791

[25]Feng L J,Xia Y J 2015Acta Phys.Sin.64 010302(in Chinese)[封玲娟,夏云杰 2015物理学报 64 010302]

[26]Yang L Q,Feng L J,Song X X,Xue L J,Man Z X 2016Acta Sin.Quantum Opt.22 6(in Chinese)[杨丽青, 封玲娟,宋晓晓,薛利娟,满忠晓2016量子光学学报22 6]

[27]Ma T T,Chen Y S,Chen T,Hedemann S R,Yu T 2014Phys.Rev.A90 042108

[28]Wootters W K 1998Phys.Rev.Lett.80 2245

[29]Li M,Fei S M,Song H S 2009J.Phys.A:Math.Theor.42 145303

[30]Sabín C,Garcia-Alcaine G 2008Eur.Phys.J.D48 435

[31]An B N,Kim J,Kim K 2010Phys.Rev.A82 032316