基于粒子群算法的平面四杆机构优化与动力学仿真

沈明秀,王荔芳

(昆明学院 自动控制与机械工程学院,云南昆明 650214)



基于粒子群算法的平面四杆机构优化与动力学仿真

沈明秀,王荔芳

(昆明学院 自动控制与机械工程学院,云南昆明 650214)

目前，平面四杆机构运动过程中连杆从动件输出的角加速度的线加速度比较大,导致机构运动不平稳,不能很好地满足工作需求.对平面四杆机构连杆及销子进行优化,实现连杆从动件输出的角加速度和线加速度值最小化.创建平面四杆机构链接节点间隙模型和机构矢量简图,对四杆机构的运动节点间隙进行分析,推导了连杆运动的质心线加速度计算公式.四杆机构连接销子采取虚拟质量,引入粒子群算法优化连杆运动参数,结合具体实例对优化前和优化后的四杆机构从动件进行运动学仿真.仿真结果显示:优化前两个从动件输出的角加速度最大值分别为2.4×103rad·s-2和-5.0×103rad·s-2,优化后两个从动件输出的角加速度最大值分别为-0.6×103rad·s-2和-0.8×103rad·s-2;优化前两个从动件输出的线加速度最大值分别为0.27×103m·s-2和0.55×103m·s-2,优化后两个从动件输出的线加速度最大值分别为-0.07×103m·s-2和0.12×103m·s-2.优化后四杆机构从动件输出的角加速度和线加速度相对较小,运动相对平稳,效果很好.

四杆机构; 粒子群算法; 角加速度; 线加速度; 优化

平面连杆机构也称之为平面低副机构,它可以按照设计的运动规律实现摆动、移动及转动等各种复杂运动.连杆机构具有许多优点:连杆运动过程中承受压强较小,接触部位便于润滑,磨损很小;制造简单方便,运动精度较高;运动行程远,两构件能够靠自身封闭来完成接触.因此,平面连杆机构应用非常广泛.主要应用在仪表、工程机械、折叠伞、机械手上.但是,平面连杆机构也存在许多缺点:当运动复杂时,机构构件数量和运动副就会增加,导致机构结构复杂,工作效率较低;机构在运动过程中所产生的惯性很大,特别是在高速运动时,难以保持平衡,振动比较大,故常常应用于低速场合.

由于四杆机构结构简单、设计方便、加工生产容易及工作比较可靠等,所以在工程机械中得到了广泛的应用.随着社会生产的发展,四杆机构承受的载荷在增加,运动速度也不断提高,对四杆机构的设计难度也在增大.因此,四杆机构在高速运动过程中如何保持平稳一直是近年来研究的重点.当前,许多研究人员对四杆机构优化进行了深入的研究,例如,文献[1-3]基于遗传算法优化了平面四杆机构角位移误差和行程比系数,通过MATLAB 软件的遗传算法,构造了优化目标函数模型,缩短了运行周期,提高了四杆机构的运动精度.文献[4-6]研究了四杆机构近似函数综合的优化设计模型,通过可行性规则差分进化算法求解函数非线性方程组.最后通过仿真验证转角误差,可行性规则差分进化算法可以提高机构转角精度.文献[7-8]研究了四杆机构的动力学特性,建立了四杆机构运动的动力学模型,分析了机构的动态应力和应变,通过有限元软件对机构进行了模态分析,得出了连杆应力集中位置,为机构的优化目标提供了参考依据.以前研究者研究四杆机构很少考虑机构运动的稳定性,导致运动过程中振动比较严重.对此,本文创建了四杆机构间隙模型,给出了四杆机构的向量简图,对四杆机构进行了运动分析,推导出了连杆质心位移和角度的计算方程式.引入三次多项式构造连杆旋转角度,通过粒子群算法优化四杆机构连杆设计参数,对四杆机构输出的角加速度和质心线加速度进行动力学仿真.结果表明:与优化前相比,优化后输出的角加速度和线加速度最大值明显下降,整体跳动幅度很小,运动相对平稳.

1 平面四杆机构

1.1 节点间隙模型

本文研究的平面四杆机构具有3个链接关节,在关节部位所产生的间隙如图1所示.对节点间隙模型进行分析,假设链接两个连杆的销子质量为零(虚拟质量),并且在刚性单元间是一种无摩擦链接.间隙矢量的方向与碰撞面的法线方向相一致,链接节点所受合力是在同一个方向上,如图2所示.另一方面,每一个节点间隙都会给链接处带来额外的自由度,链接点的受力方向就是合力方向.

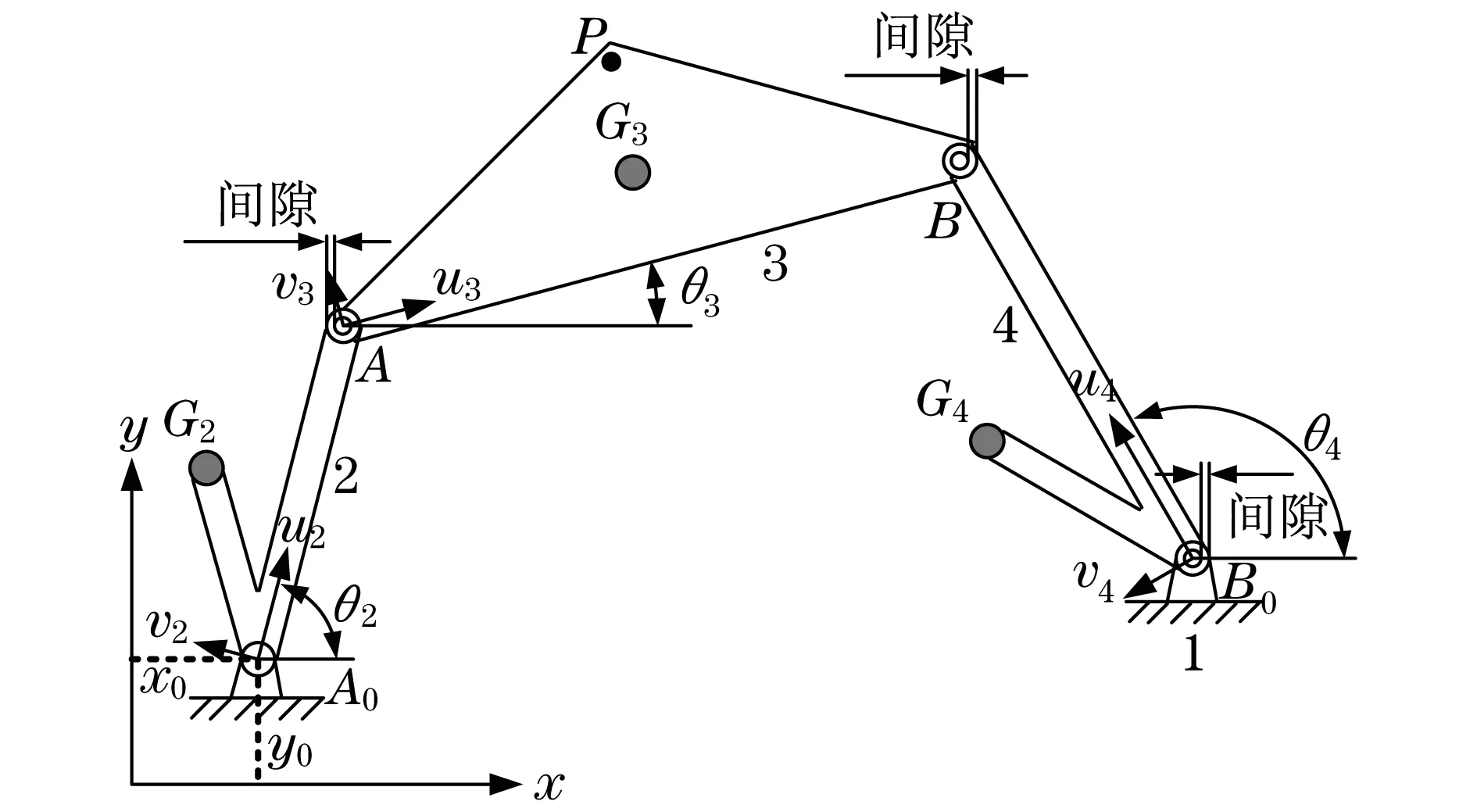
图1 四杆机构间隙模型Fig.1 Four-bar linkage clearance model

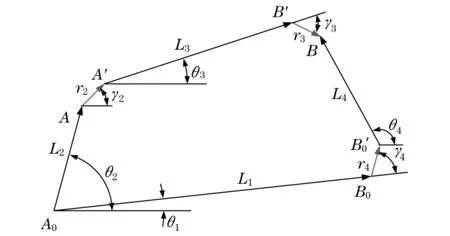
图2 四杆机构向量简图Fig.2 Four-bar linkage vector diagram

1.2 运动学分析

运动学主要是对平面四杆机构的位移、速度及加速度进行分析.由图2可知,矢量闭合方程式为

(1)

式中:Li表示第i个连杆的长度;θi表示第i个连杆与水平面之间的夹角;rj表示第i个链接销子的半径;γj表示第i个链接销子与水平面之间的夹角.

由图1可知,P点的坐标方程式为

(2)

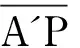
因此,连杆质量中心坐标的方程式如下所示:

(3)

(4)

(5)

式中:Gi表示第i个连接杆的质量中心;ui和vi表示Gi点在自身质量分布坐标系统里的值(i=2,3,4).

式(3)～(5)对时间的微分方程式就是连杆质心的速度和加速度.

2 运动综合

平面连杆路径生成问题中的尺度合成包括确定的连杆尺寸以产生P点所需的路径.因此,我们设计出平面四杆机构以解决节点间隙在被动节点下的路径生成问题.路径生成问题中的若干设计参数都以向量的形式表示:

(6)

式中:N是优化目标节点的个数,在此,目标函数由两部分组成,即位置误差和通过补偿函数建模引入的约束.通常而言,在路径再现综合问题中,前者是定义为在所产生路径与所期望路径之间的均方距离的总和,而后者被定义为一些不等式约束.在此,一般有5种约束,即格拉斯霍夫定律、旋转输入链接、点缺陷、分支缺陷、回路缺陷.四杆机构的格拉斯霍夫定律方程式[9]为

(7)

(8)

式中:p和q是链接节点的中心长度.

对于一个完整的旋转输入链接,格拉斯霍夫定律方程式[9]为

(9)

假设给出了曲柄逆时针旋转模型,分支和回路的缺陷约束条件为

(10)

(11)

(12)

因此,具有上述约束的路径生成合成目标函数[10]定义如下:

(13)

3 链接销子计算

虽然平面四杆机构运动是单自由度系统,但是由于节点间隙的存在,又将额外增加3个不可控的自由度.因此,这些自由度应得到控制以减小一些负面影响,如果链接假定为刚性,链接销子的方向可通过拉格朗日方程[11]获得:

(14)

式中:T,U和D分别表示动能、势能和耗散函数.

(15)

(16)

(17)

式中:i表示节点数量;mi表示质量;Ii表示转动惯量;g表示重力加速度;Cθi表示黏性阻尼系数;Cγi表示链接销子质量.带入方程(14),简化如下:

(18)

3.1 粒子群优化算法

粒子群优化算法[12]是一种基于迭代的优化算法.粒子群算法开始产生一组随机的粒子群体,通过搜索和迭代找到最佳值.粒子群优化算法通过迭代来更新粒子的位置和速度,其计算表达式[12]为

(19)

(20)

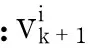
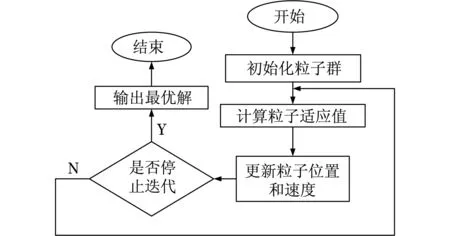
图3 粒子群优化算法流程图Fig.3 Flow chart of particle swarm optimization algorithm

粒子群优化算法设计链接节点,节点的方向角度是以曲柄角为自变量的函数,即γjd=f(θ2)(j=2,3,4).在优化过程中,该方向假定是理想的方向,当角速度可知的情况下,节点的方向可以通过控制销子质量分布来控制.因此,四杆机构的优化参数为

(21)

因此,优化目标值是实际与理想角度差的平方和作为曲柄角的一个周期,如下所示:

(22)

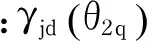
平面四杆机构在实际运动过程中,链接销子与链杆之间总是存在间隙.优化的四杆机构,它遵循期望的路径,且没有对虚拟质量方向产生干扰变化,通过使用如下三次多项式[13]:

(23)

式中:P1j,P2j,P3j,P4j表示系数.

假定链接销子与连杆之间的间隙为0.5mm,设计参数X1,如表1所示.

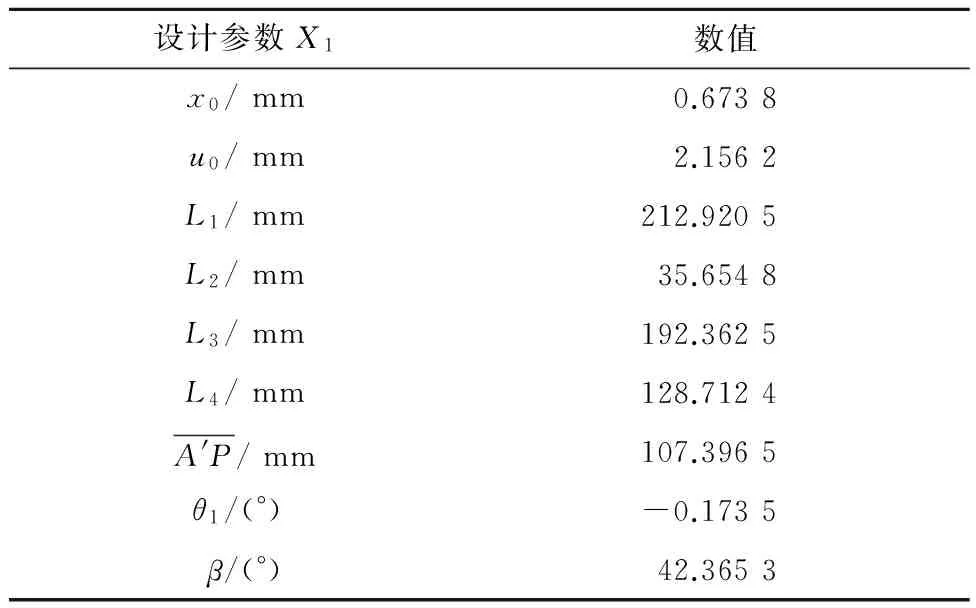
表1 设计参数

采用粒子群优化算法得到三次多项式系数和优化参数X2分别如表2和表3所示.

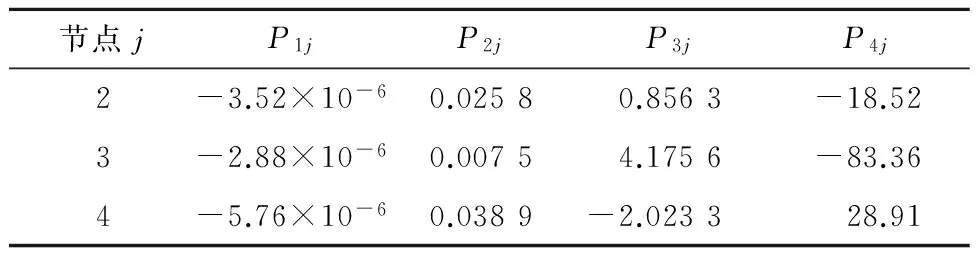
表2 四杆机构的节点间隙系数

4 运动仿真及分析

对优化前和优化后的平面四杆机构的角加速度和线加速度进行动力学仿真,仿真参数设置如表3所示,连杆L2的角速度为4π/s,仿真时间为

表3 X2优化前和优化后的参数

1.0 s.连杆L3和L4的角加速度仿真结果分别如图4,5所示,连杆L3和L4线的加速度的仿真结果分别如图6,7所示.

从图4,5可知,优化后四杆机构连杆L3,L4的角加速度输出值波动幅度较小,连杆L3,L4的角加速度输出最大值分别为-0.6×103rad·s-2和-0.8×103rad·s-2;优化前四杆机构连杆L3，L4的角加速度输出值波动幅度较大,连杆L3，L4的角加速度输出最大值分别为2.4×103rad·s-2和-5.0×103rad·s-2,角加速度容易发生突变现象.从图6,7可知,优化后四杆机构连杆L3,L4的质心线加速度输出值波动幅度较小,连杆L3,L4的质心线加速度输出最大值分别为-70 m·s-2和120 m·s-2;优化前四杆机构连杆L3,L4的质心线加速度输出值波动幅度较大,连杆L3,L4的质心线加速度输出最大值分别为270 m·s-2和550 m·s-2,连杆L3,L4的质心线加速度容易发生突变现象.因此,优化后四杆机构连杆输出的角加速度和线加速度变化较小,运动比较平稳,机构不容易产生振动.

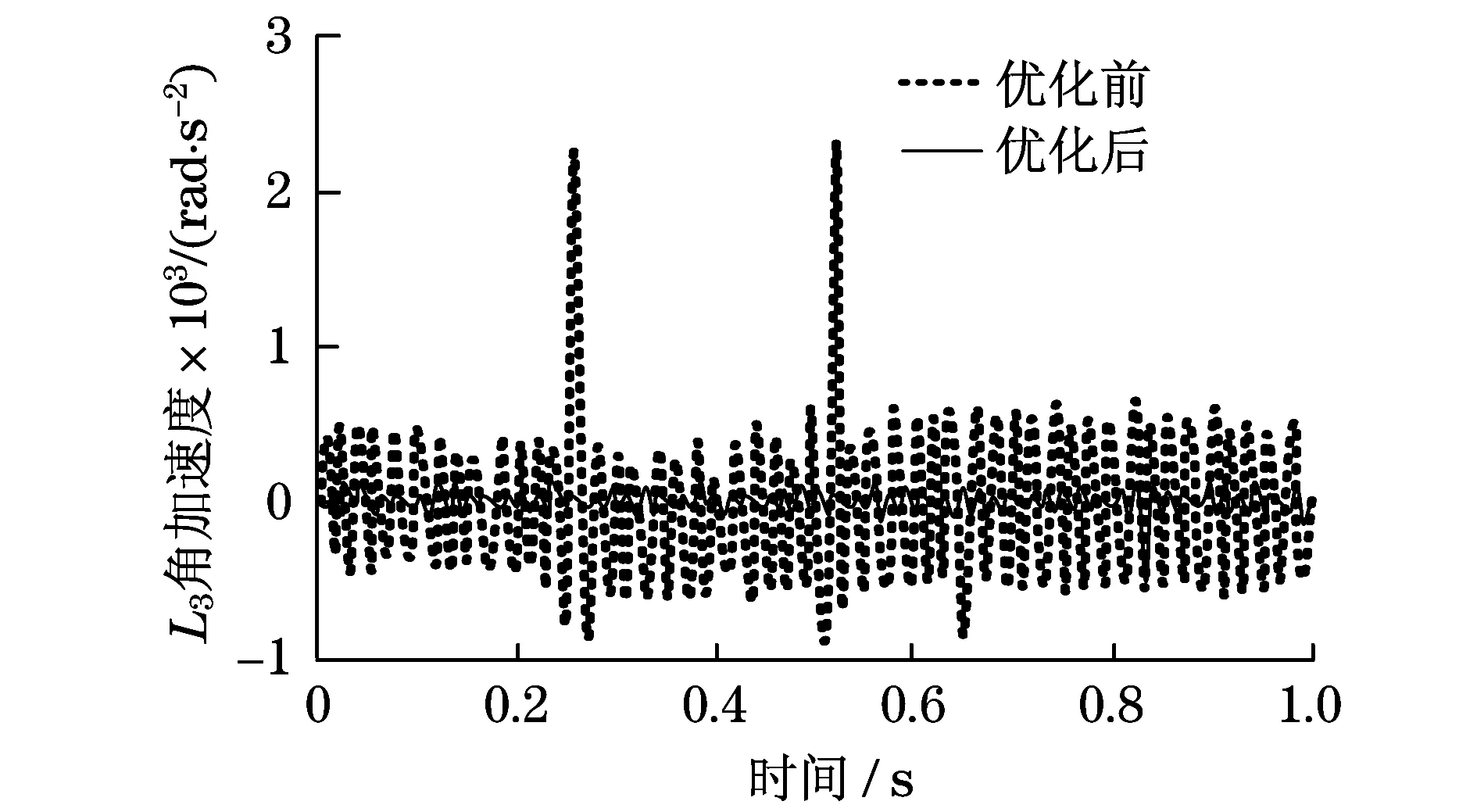
图4 连杆L3角加速度Fig.4 Connecting rod L3 angular acceleration

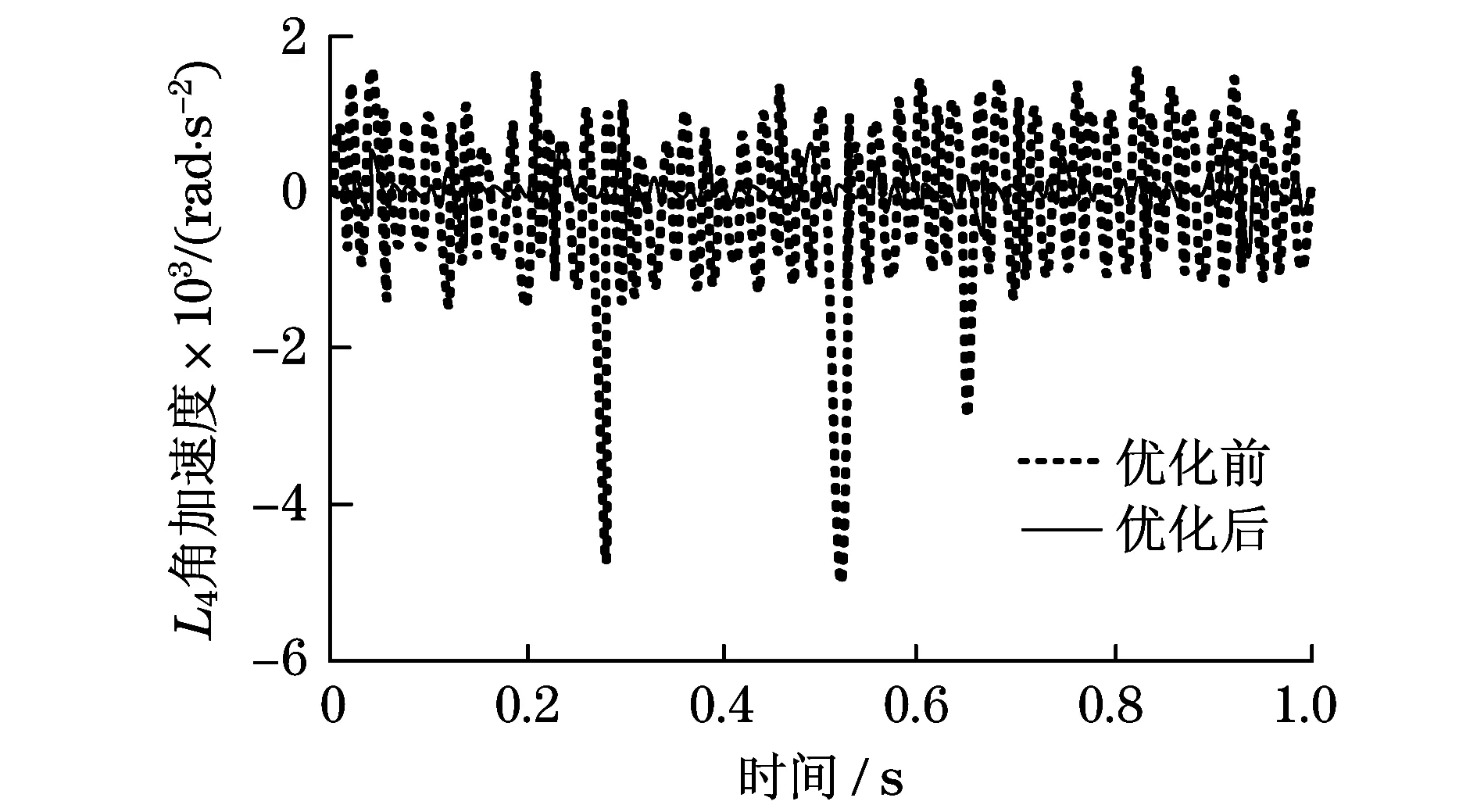
图5 连杆L4角加速度Fig.5 Connecting rod L4 angular acceleration

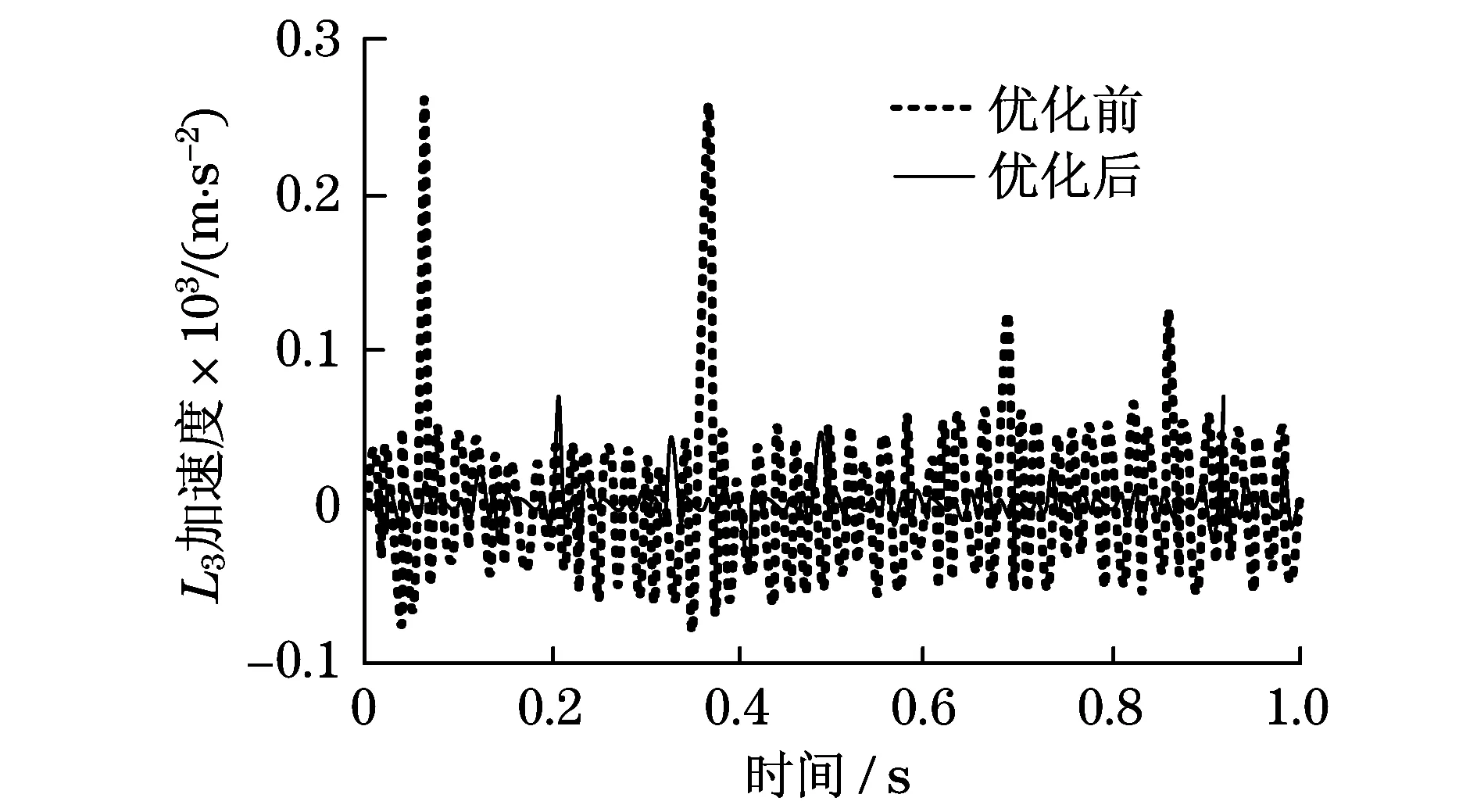
图6 连杆L3质心线加速度Fig.6 Connecting rod L3 centroid acceleration

图7 连杆L4质心线加速度Fig.7 Connecting rod L4 centroid acceleration

5 结语

针对平面四杆机构连杆节点存在间隙、导致机构运动不平稳等问题,本文采用粒子群算法优化了四杆机构连杆及销子的设计参数.构造了四杆机构的间隙模型及向量简图,推导出了四杆机构的运动位移数学计算公式,确定了四杆机构销子质量计算.优化了目标函数,通过粒子群优化算法搜索出连杆的最优尺寸设计参数,借助于MATLAB软件对优化后四杆机构连杆输出的角加速度和线加速度进行了仿真.仿真结果表明:优化后连杆输出的角加速度和线加速度最大值明显下降,整体抖动较小,为平面四杆机构运动学的研究提供了参考依据.

[1] 张晓霞.遗传算法在机械设计优化中的应用及运动学仿真技术研究[D].太原:中北大学,2008.

ZHANG X X.Application of genetic algorithm in mechanical optimization design and dynamic simulation research[D].Taiyuan:North University of China,2008.

[2] KHORSHIDI M,SOHEILYPOUR M,PEYRO M,et al.Optimal design of four-bar mechanisms using a hybrid multi-objective GA with adaptive local search[J].Mechanism and Machine Theory,2011,46(5):1454-1464.

[3] 崔永波.遗传算法视域下平面四杆机构优化设计[J].煤炭技术,2012,31(9):6-8.

CUI Y B.Genetic algorithm horizon of planar four-bar optimization design research[J].Coal Technology,2012,31(9):6-8.

[4] 车林仙,杜力,黄勇刚.球面四杆机构函数综合的带修复策略可行性规则差分进化算法[J].机械工程学报,2015,51(11):32-39.

CHE L X,DU L,HUANG Y G.Feasibility-rule-based differential evolution algorithm with repair strategies for function synthesis of spherical four-bar linkages[J].Journal of Mechanical Engineering,2015,51(11):32-39.

[5] BULATOVICR R,MIODRAGOVIC G,BOSKO M S.Modified Krill Herd(MKH)algorithm and its application in dimensional synthesis of a four-bar linkage[J].Mechanism and Machine Theory,2016,95(9):2-19.

[6] 汪从哲,方跃法.基于差分进化算法的平面四杆机构轨迹和速度双目标优化综合[J].北京交通大学学报,2011,35(6):73-77.

WANG C Z,FANG Y F.Optimal synthesis of path and velocity of planar four-bar mechanisms using an evolutionary algorithm[J].Journal of Beijing Jiaotong University,2011,35(6):73-77.

[7] 李姣.平面柔顺四杆机构动力学特性分析与优化[D].太原:中北大学,2013.

LI J.Dynamics analysis and optimization of planar compliant four-bar mechanism[D].Taiyuan:North University of China,2013.

[8] YILDIZ A,KOPMAZ O,TELLI S.Dynamic modeling and analysis of a four-bar mechanism coupled with a CVT for obtaining variable input speeds[J].Journal of Mechanical Science and Technology,2015,29(3):1001-1006.

[9] KIMB S,YOO H H.Unified synthesis of a planar four-bar mechanism for function generation using a spring-connected arbitrarily sized block model[J].Mechanism and Machine Theory,2012,49(6):141-155.

[10] KIMJ W,SEO T W.A new design methodology for four-bar linkage mechanisms based on derivations of coupler curve[J].Mechanism and Machine Theory,2016,100(3):139-152.

[11] AFFIZEL-KRIBI B,ROMDHANE L.Advanced mechatronic design using a multi-objective genetic algorithm optimization of a motor-driven four-bar system[J].Mechatronics,2007,17(6):490-498.

[12] 段旭洋,王皓,赵勇,等.基于嵌套粒子群算法的平面机构尺度综合与构型优选[J].机械工程学报,2013,49(13):33 -38.

DUAN X Y,WANG H,ZHAO Y,et al.Dimensional synthesis and optimal type selection of planar mechanisms based on nested particle swarm optimization[J].Journal of Mechanical Engineering,2013,49(13):33-38.

[13] 李浩,黄艳,马岩蔚.基于三次多项式曲线的轨迹平滑压缩算法[J].组合机床与自动化加工技术,2016(6):13-15.

LI H,HUANG Y,MA Y W.The smooth compression algorithm based on cubic polynomial curve[J].Modular Machine Tool & Automatic Manufacturing Technique,2016(6):13-15.

Optimization and dynamical simulation on planar four-bar mechanism based on particle swarm optimization algorithm

SHEN Mingxiu, WANG Lifang

(College of Automatic Control and Mechanical Engineering,Kunming University,Kunming 650214,Yunnan,China)

Currently,the angular acceleration outputs from connecting rod followers of planar four-bar mechanism are so large yet unstable that cannot meet working demands.To optimize the planar four-bar linkages and pins,the connecting rod outputs of angular and linear accelerations are initially minimized. Afterwards,the planar four-bar linkage joint gap model and vector diagram are established.Thereafter,the kinematic joint gap of four-bar mechanism,together with the formula of connecting rod motion,is derived from the linear acceleration of centroid. Since the connecting pins of four-bar mechanism possess virtual mass,the particle swarm optimization is employed for motion parameters of connecting rods. By using specific examples for kinematics simulation on four-bar mechanism followers,it is indicated that the pre-optimization values of maximum angular acceleration for two followers are respectively 2.4×103rad·s-2and -5.0×103rad·s-2， whereas the post-optimization values of maximum angular acceleration for two followers are respectively -0.6×103rad·s-2and 0.8×103rad·s-2. In addition,the pre-optimization values of maximum linear acceleration for two followers are respectively 0.27×103m·s-2and 0.55×103m·s-2, whereas the post-optimization values of maximum linear acceleration for two followers are respectively -0.07×103m·s-2and 0.12×103m·s-2. Conclusively,the angular and linear accelerations are smaller after optimization,whilst the movement is more stable with better effect.

four-bar linkage; particle swarm optimization; angular acceleration; linear acceleration; optimization; simulation

云南省教育厅科学研究基金重点资助项目(2010Z027)

沈明秀(1978-),女,讲师,硕士.E-mail:shenxm201607@126.com

TH 112

A

1672-5581(2017)01-0015-06