利用DSO的REF功能测量超声波速度

聂 明

(东北石油大学大学物理实验中心，黑龙江 大庆 163318)



利用DSO的REF功能测量超声波速度

聂 明

(东北石油大学大学物理实验中心，黑龙江 大庆 163318)

超声波传播速度的测量，在测距与定位、液体流速测定、弹性模量测量、气体温度瞬间变化测量等方面的应用中十分重要。文中给出一种基于接收信号延迟时间的较直观的声速测量方法，其中延迟时间的测量是充分利用了数字存储示波器对信号的多种降噪处理方法，并且利用了数字存储示波器的参考波形(REF)功能对接收信号进行整体对准实现的。实验证明这种方法的测量结果相当准确，为声速的精密测量提供了一种新的思路。这种方法可应用在大学基础物理实验或课堂演示教学环节，可使学生对声速测量的原理和过程有更加直观的认识。对启发学生灵活使用及充分发挥仪器的功能都有一定的借鉴作用。

数字存储示波器；REF；数字滤波；带宽限制

1 导言

声波在空气介质中以纵波传播。声波的波长、强度、传播速度等是声波的重要性质。而超声波传播速度的测量，在测距与定位、液体流速测定、弹性模量测量、气体温度瞬间变化测量等方面的应用中具有重要意义。在通常的大学物理实验课程中，超声波声速的测量原理，有的是基于波动理论中的关系式[1-3]：v=f×λ进行的。其中超声波的频率f就等于为压电陶瓷换能器提供超声频段激励的信号源频率，而波长λ可采用“驻波法(共振干涉法)”“双踪相位比较法”“李萨如图形相位比较法”等方法测量。还有的是利用“时差法[4,5]”测量声速，即利用公式：v=L/t，其中距离L为发射换能器与接收换能器之间的距离，t为超声发射波与接收波之间的间隔时间。时差法虽然是超声波在实际应用中，如测距、液位检测等的理论基础，但在学生实验中时间t的测量是由声速测定仪自动测量完成的，测定仪显示屏上只是显示一个时间值，而且这个时间常会因为距离的变动和接收增益的调节问题不时出现跳变，不容易准确的判定。对于学生而言这相当于一个“黑匣子”实验，这些都不利于对学生进行实验操作及分析解决问题等方面的训练和相关知识的理解。

为此，设计了基于接收信号延迟时间的较直观的空气媒质中超声波声速测量实验，其中延迟时间的测量是充分利用了数字存储示波器对信号的多种降噪手段以及参考波形(REF)整体对准功能完成的，实验证明测量结果相当准确。此实验项目可以避免上述“时差法”的诸多问题，同时对训练学生充分利用数字存储示波器的强大数据处理及分析功能亦有所裨益。

2 测量原理及脉冲串参数选择

声速测量试验装置如图1所示，包括双通道数字存储示波器(DS1102E)、具有猝发功能的DDS函数信号发生器(SPF05A)、谐振频率匹配的一套压电陶瓷换能器(PZT)、带有容栅式距离测量数显表头的声速测量支架(SV7)、BNC接口同轴电缆、T形BNC三通等。

众所周知，在确定的温度及压力下，超声波在组分一定的空气中以确定的有限的速度传播。利用函数信号发生器输出的短脉冲信号(脉冲调制正弦波)作为发射换能器S1的激励信号，则发射传感器响应出超声信号并以一定的速度传播出去。因接收传感器S2与发射传感器有一定的距离L，则接收传感器的激励声压信号相对发射传感器输出的超声信号有一定的延迟时间t。可以利用距离与延迟时间之间的关系计算出超声波的传播速度，测量原理如图2所示。当测量出L和t后即可由v=L/t计算出声速。

DDS函数信号发生器的猝发功能模式(Burst)

图1 声速测量试验装置

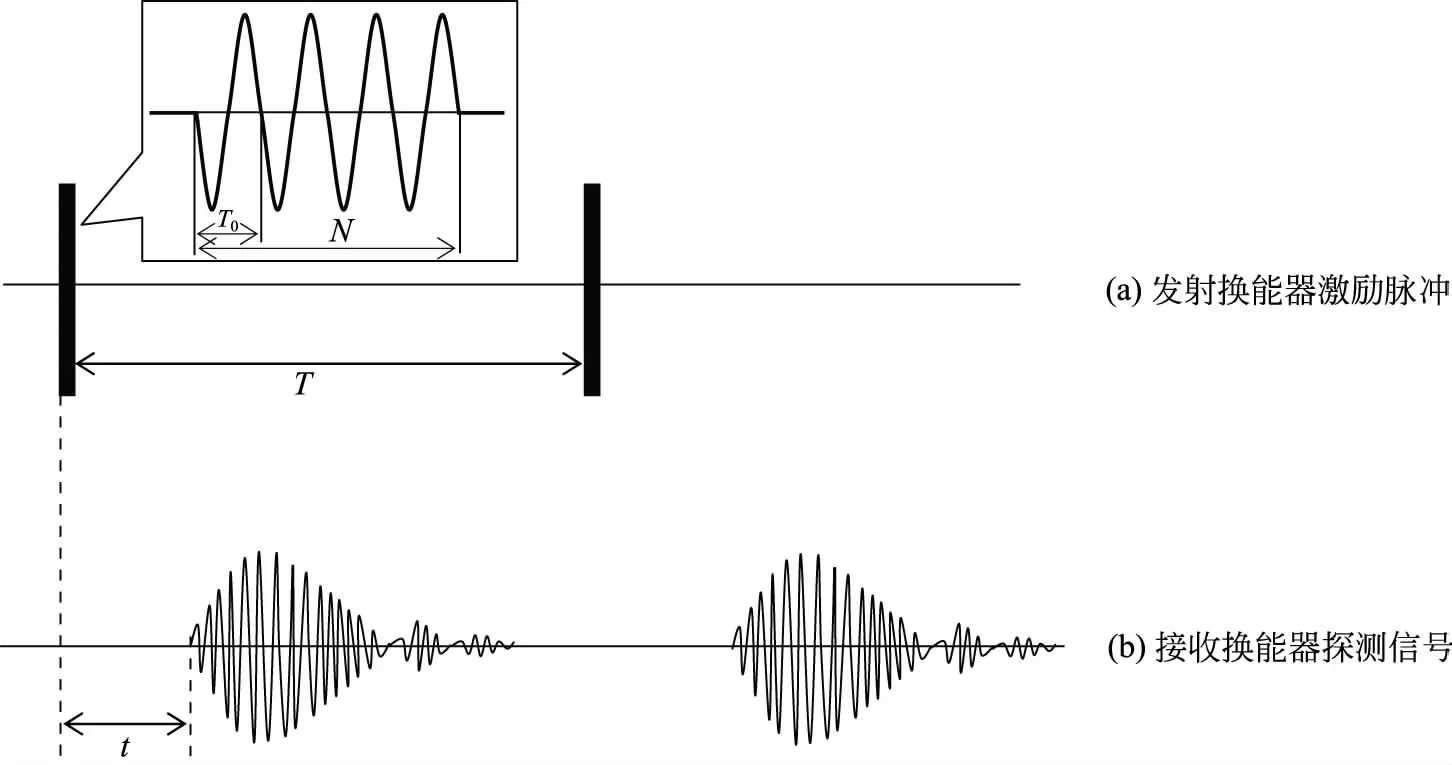
图2 基于延迟时间的声速测量原理

图3 猝发输出时间对接收换能器响应的影响

可以输出一定周期数的频率不变的脉冲串信号，作为发射传感器S1的激励信号。无论是片状或管状PZT，都有一定的共振频率，在这些频率附近能量转换效率较高，所以如图2(a)所示，T0要调节到与所用的换能器共振频率f0相匹配，所以信号源在猝发功能模式时对猝发输出的正弦信号的频率要调节到f0。当作激励信号的脉冲串信号的周期个数N不同时，接收换能器探测到的信号幅度有很大的变化，如图3所示。Upp为一定距离下接收换能器探测到的直达波的峰峰值电压，可见为了增强探测信号的幅度，猝发输出的正弦信号持续作用时间愈长愈好，即周期个数N越多越好。而对于相邻两个猝发信号的间隔时间T，由图3可知越长越好，即脉冲信号的重复频率要低，最短也要保证由前一个激励脉冲引起的响应衰减完毕之后才可以发射下一个声脉冲，否则就会前后信号混淆，无法对延迟时间t进行测量。

3 延迟时间的REF测量

简单的应用v=L/t公式计算声速并不精确。原因之一，声程L很难精确测量。在利用超声换能器进行测试中，超声波并不是直接进入被测材料的，而是在换能器内部产生超声波，再通过一定的媒质使超声波进入测试材料内部。因此，超声波产生后在介质中传播的声程包括换能器内部的声程和被测材料中的声程；原因之二，延迟时间t因为很多因素也难以精确测量。延迟时间t本应该是超声波在待测材料中的传播时间，但实际上还包括了额外的延迟时间[6]，如电路滞后延时、电缆延时、触发延时、换能器延时、衍射延时等。额外的延迟时间是极难精确测定的，换能器内部的声程也是不容易测到的。但是它们中很多项在一个确定的测试装置中都是固定不变的，所以可以采用数据处理的方法减小这些误差。设接收换能器在距离坐标为x1时，对应的接收信号时间坐标为t1。而当接收换能器在距离坐标为x2时，对应的接收信号时间坐标为t2。则t2与t1之差就仅仅是由于待测材料中距离的变化x2-x1所带来的，所以可以利用公式v=(x2-x1)/(t2-t1)来计算测试材料的声速。

虽然理论上可以利用公式v=(x2-x1)/(t2-t1)对材料中的声速进行精确测量，但实际还存在问题。由于空气特性声阻抗[7]非常小，是超声波的不良媒质。而换能器表面特性声阻抗又非常大，导致声波反射很强而透射很弱，即两者之间耦合得很差，接收信号因距离增大而衰减很快。在图4(a)中，信号在工频干扰之上又混有很多高频噪声，在利用了DSO垂直通道中的带宽限制与高通数字滤波，并且数据获取方式采用256次平均采样后，换能器接收信号上的高频干扰噪声及工频50Hz干扰得到较大改善，如图4(b)所示。

图4 距离较大时换能器接收的信号波形

图5 换能器起振过程

由于低频超声波在发射和接收过程中存在一个较长时间的起振过程，见图5。尤其是当距离L较大时，接收信号受环境噪音等干扰的影响就会变得更大，即使经过降噪处理之后，信号仍然不理想，如图4(b)。即在时延之前和之后接收换能器采集的信号波形没有明显的能分辨的特征点，同时接收信号幅度因距离增大而衰减很快，所以要想采用在信号波形上选一个固定参考点或固定振幅阈值的做法来确定信号对应的时间坐标必然会引入较大的人为误差。显然由此所带来的精度损失在短距测量中会更加明显，因此有必要对接收信号所对应的时间坐标如何精确的测定进行研究。

对于延迟时间的精确测量方法，近年来有不少的研究与分析。例如通过温差补偿[8]、阈值可调、回波包络[9]等方法来提高超声系统的精度，由于这些方法对硬件及技术要求较高、并且数据处理量较大等原因而受到限制。虽然接收换能器采集的信号在时延之前和之后的波形上没有明显的能分辨的特征，如波前或波峰等，由于是逐渐起振的并且在距离较大时起振点处的一段范围湮没在背景噪声中，找不到一个可以准确参考的固定点位。虽然无法找到一个确切的参考点，但是可以以接收信号的整体作为参考点。虽然在距离较大时信号上混有干扰和噪声，但其整体的形貌是固定不变的。取接收换能器移动到待测的距离处的探测信号作为参考用波形，此参考波形与接收换能器再次移动到原位置的波形是密切相关的，即信号只有强度的变化，而波型变化甚微，干扰噪声与信号是无关的。为此，可以采用数字示波器的参考波形(REF)功能，来实现利用接收信号的整体作为测量延迟时间的参考。

图6 参考波形与被测信号重合的情况

在调节参考波形与被测的接收信号重合的过程中，要充分利用示波器垂直档位调节功能，交替使用粗调和微调两种模式来改善波形显示的幅度，以利于信号细节的观察，使两个波形完全重合。利用参考波形测量延迟时间的过程如图7所示。测量中要适当调节水平扫描速度，测量时间时在参考波形上任选一个固定的位置作为计时参考点即可，因为参考波形是固定的。还要特别注意在每次测量过程中，信号触发位置相对于视窗中点的水平距离即当前波形窗口的触发位置不可以移动，见窗口右下角显示“T→1.152ms”，否则时间测量错误。当参考波形与被测信号波形重合时，可通过垂直旋钮使两信号上下错开以利于手动调整光标进行测量。测量数据如表1所示。

为了衡量测量结果的准确度，需与理论声速进行比较。考虑到环境温度t和相对湿度r等的影响，空气中理论声速计算公式为[10]

v0=331.45

图7 利用参考波形测量接收信号的时间坐标

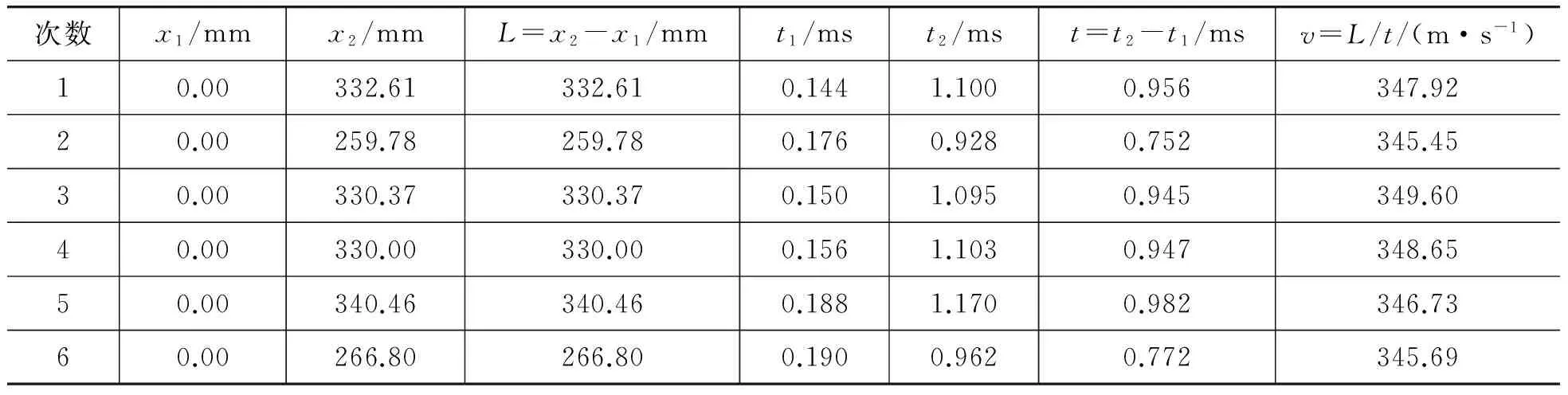
次数x1/mmx2/mmL=x2-x1/mmt1/mst2/mst=t2-t1/msv=L/t/(m·s-1)10.00332.61332.610.1441.1000.956347.9220.00259.78259.780.1760.9280.752345.4530.00330.37330.370.1501.0950.945349.6040.00330.00330.000.1561.1030.947348.6550.00340.46340.460.1881.1700.982346.7360.00266.80266.800.1900.9620.772345.69

根据测量数据，并考虑到数显表头对距离测量和DS1102E数字存储示波器对时间测量带来的B类标准不确定度，以及由于数据的分散性带来的A类标准不确定度，综合考虑上述因素，可得到具有可靠性评价指标(测量不确定度)的声速测量结果：

理论声速为：v0=348.14m·s-1

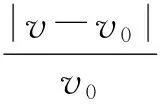
4 结语

这里介绍的方法,与测量绝对声速精度最高的一种方法即脉冲回波重合法[11]有一些相通之处，但又避免了硬件的设计与制作。这种方法直接利用了DSO具有的REF功能，是利用信号的整体来对延迟前后的换能器接收信号的波形整体进行时间定位测量。由于是利用信号的整体进行对准定位，对信号混有的噪声容限很高，定位准确，延迟时间测量的精度很高，所以声速测量结果的误差很小。

在这种声速测量方法中，并没有增加对换能器接收的信号进行前置放大环节。其原因，一是在已有的装置中接收换能器可移动的距离有限，虽然信号较弱且信噪比低，但通过增加示波器垂直通道灵敏度以及采用多种降噪措施之后幅度已经足够；二是为了演示即使不需增加任何仪器，利用现有的硬件和采用灵活的方法，也可以达到开拓思路扩展实验的目的。这种方法可应用在大学基础物理实验及课堂演示教学环节，可使学生对声速测量的原理和过程有更加直观的认识，也可应用于声波近场区传播规律的研究等。同时在操作过程中也可以让学生了解数字存储示波器具有的一系列信号处理的功能，这对启发学生如何将现有仪器功能发挥到极致有一定的借鉴作用。

[1] 李朝荣.基础物理实验[M].北京:北京航空航天大学出版社,2013.Li Chaorong. Basic physics experiment[M]. Beijing: Beijing University Press, 2013. (in Chinese)

[2] 孙存英,俞嘉隆,乔卫平.超声波探测技术原理实验[J].大学物理实验,2010,23(1):1-3. Sun Cunying, Yu Jialong, Qiao Weiping. The Experiment on the principle of the ultrasonic measurement[J]. Physical Experiment of College, 2010, 23(1): 1-3. (in Chinese)

[3] 熊永红.大学物理实验[M].武汉:华中科技大学出版社,2004. Xiong Yonghong. University physics experiment[M]. Wuhan: Hua zhong University of Science and Technology Press, 2004. (in Chinese)

[4] 徐斌.一种考虑起振延迟的低频超声波短距高精度测量校准方法[J].传感技术学报,2013,26(5):666-669. Xu Bin. Identifying and calibrating start-up delay in short-range high-precision measurement with low-frequency Ultrasonic[J]. Chinese Journal of sensors and Actuators, 2013, 26(5): 666-669. (in Chinese)

[5] 石星军.大学物理实验[M].北京:国防工业出版社,2006. Shi Xingjun. University physics experiment[M]. Beijing: National Defense Industry Press, 2006. (in Chinese)

[6] 王寅观.超声波速度的精密测量理论及其应用[J].声学技术,1989,2:18-23. Wang Yinguan. Precision measurement theory and applications of ultrasonic velocity[J]. Acoustic Technology, 1989, 2: 18-23. (in Chinese)

[7] 布利茨.超声技术及应用[M].李东林,译.北京:海洋出版社,1992.

[8] 樊帆,踞晓涛,贾佳.新型远距离超声测距系统设计[J].工业控制计算机,2013,26(4):117-120. Fan Fan, Ju Xiaotao, Jia Xin. A new design of large sensing—range ultrasonic ranging system[J]. Industrial Control Computer, 2013, 26(4): 117-120. (in Chinese)

[9] Ramos P M, Fonseca da Silva M, Cruz Serra A. Low frequency impedance measurement using sine-fitting[J]. Measurement, 2004, 35(1): 89-96.

[10] 周怡,金君.大学物理实验[M].武汉:武汉理工大学出版社,2012. Zhoy Yi, Jin Jun. University physics experiment[M]. Wuhan: Wuhan University of Technology Press, 2012. (in Chinese)

[11] 王寅观.用脉冲法测量超声波传播速度[J].实验技术与管理,1982,2(3):24-27. Wang Yinguan. Ultrasonic wave propagation velocity measured with a pulse method[J]. The Experimental Technology and Management, 1982, 2(3): 24-27. (in Chinese)

■

ULTRASONIC VELOCITYMEASUREMENT BY USING REF FUNCTION OF DSO

Nie Ming

(College Physics Experimental Center, Northeast Petroleum University, Daqing Heilongjiang 163318)

Measuring ultrasonic velocity plays a vital role in ranging and localization, liquid flow-rate measurement, elastic modulus measurement, transient gas temperature change measurement and other applications. A straightforward sound velocity measuring method which is based on delay time in receiving signal is presented in this paper, and measuring delay time is presented by fully using noise reduction treatments of digital storage oscilloscope on signal and taking advantage of REF function of digital storage oscilloscope to achieve integral calibration. The experiment testifies that measurements are fairly accurate and a new thread of thought is provided for accurate sound velocity measurement. This method can be applied in the basic college physics experiment or the demonstration teaching in classroom, which enables students to intuitively understand the principle and process of sound velocity measurement, and has certain references to inspire students’ flexible and full use of the function of instruments.

digital storage oscilloscope; REF; digital filter; bandwidth limit

2016-07-12

聂明，男，讲师，主要从事物理实验教学科研工作,研究方向为磁电与偏振光检测等，nieming_2008@126.com。

聂明. 利用DSO的REF功能测量超声波速度[J]. 物理与工程，2017，27(3)：30-35.