中国初中数学教材中勾股定理内容编写特点研究

宋运明



中国初中数学教材中勾股定理内容编写特点研究

宋运明

（贵州师范大学数学科学学院，贵州贵安新区 550025）

教材特色化与核心素养培育是当今时代赋予数学教材编写的重任．采用内容分析法对中国初中数学教材中勾股定理内容编写特点进行研究，发现10个版本教材既有诸多共性，又各具特色．针对教材不足，建议完善过程性内容，增强数学核心素养落实的有效性；适当增加论证思路的种类，进一步凸显数学教材编写特色；挖掘多元文化素材，适度扩大数学史的内容范围．

数学教材；编写特点；勾股定理；核心素养；内容分析法

勾股定理是具有学科和核心素养发展双重价值的数学内容，已成为世界上大多数国家初中数学教材内容的必选．定理本身只是一个直角三角形三边边长之间简洁的代数关系，但是它所包含的推论却是无比深远广泛，它是欧氏空间至精至简的主角[1]．它是联系数与形的第一定理；它导致不可公度量的发现，引发了第一次数学危机；它开始把数学由计算和测量的技术转变为论证与推理的科学；它是证明方法最多的定理，这些证明既验证了勾股定理又大大丰富了研究问题的思想和技巧[2]，还具有丰富的数学文化价值．勾股定理对培养学生几何直观、推理能力和应用意识等数学核心素养具有重要作用．

已有不少学者对数学教材中的勾股定理内容进行了研究，包括国内外横向比较，如朱哲等的“中日新数学教科书中的‘勾股定理’”[3]，吴增生等梳理了国内外数学教材中“勾股定理”的多种呈现方式[4]；国内纵向演变，如王艳青的“中学数学教科书中勾股定理内容编排的演变研究（1949—2011）”[5]；编写与实验，如朱哲的“数学教科书中勾股定理单元的编写与教学实验研究——基于‘数学史融入数学课程’理念”[6]，等等．此外还有从数学教学[7~8]、多元文化[9]和教师知识[10]等视角对勾股定理进行的研究．它们为分析框架的形成提供了启示，但运用内容分析法，对国内现行教材中勾股定理内容实施横向比较的研究较为鲜见．教材特色化与核心素养培育是当今时代赋予数学教材编写的重任，教材是教学的重要依据．对中国现行初中数学教材中勾股定理内容的编写特点及其核心素养体现进行探析，提出有针对性的建议，这对优化勾股定理内容的教材设计、改进教学，具有现实意义．

1 研究设计

研究方法主要采用内容分析法．其核心是根据既有理论，发展系统的分析框架，将待分析的教材文本登录为一定的类属，再加以统计，以量化数据来描述该文本特性[11]．

1.1 研究对象

研究对象是教育部公布的“2016年义务教育教学用书目录”[12]中的初中数学教材（六三学制），共10个版本，全部基于《义务教育数学课程标准（2011年版）》（以下简称2011课标）而编写．它们分别由北京出版社、北京师范大学出版社、河北教育出版社、湖南教育出版社、华东师范大学出版社、江苏凤凰科学技术出版社、青岛出版社、人民教育出版社、上海科学技术出版社和浙江教育出版社出版；相应地，将其分别简称为北京版、北师版、冀教版、湘教版、华师版、苏教版、青岛版、人教版、上科版和浙教版，下同．具体内容是各版教材中的“勾股定理及其应用”[13~22]，不包括勾股定理的逆定理及其应用．

1.2 分析框架

分析框架是以教材特色化与数学核心素养落实为指导思想，在对研究对象与相关文献反复对照分析的基础上，将黄荣金分析勾股定理课堂教学的框架[7]进行扩充和改编而成．具体包括6个一级维度：所在章节、定理发现、定理描述、定理论证、定理应用和定理历史．

（1）所在章节．为刻画“勾股定理及其应用”在初中数学知识体系中的位置、地位及其在教材中所占篇幅，对该内容有个大致了解，从所在章名，章引言、前后章名与占小节数4个二级维度对教材进行分析．其中占小节数是指“勾股定理及其应用”由几个小节组成．“课堂练习”在各版本的名称不尽相同，为研究方便，将具有课堂练习功能的栏目统称为“课堂练习”．小节的划分以小节后的“课堂练习”为标志，即是出现“课堂练习”，便视为一小节内容结束．有的小节内容中除“勾股定理及其应用”外，还含一些其他内容，如勾股定理的逆定理，研究也将该小节视为“勾股定理及其应用”内容的一个小节．

课堂教学是学校教育的主阵地．限于篇幅，后面5个一级维度的分析仅限于课堂教学中使用率较高的教材内容，即是“勾股定理及其应用”所在的小节内容；不涉及小节内容之外的习题、阅读材料等．

（2）定理发现．通过特例、直观推理、逻辑演绎3种途径发现定理．所谓直观推理，指在推理过程中，对某些图形的直观特征直接加以应用，而不进行演绎推理．所谓逻辑演绎，指在推理过程中，对某些图形的直观特征进行演绎推理后再加以应用．如图2中的其中一个四边形是正方形（但不是已知，已知另一个四边形是正方形），若推理过程中对此仅从直观上判断而不加以演绎推理就当作结论使用，则视该过程为直观推理；反之，若对此演绎推理论证后再使用，则视该推理过程为逻辑演绎．

（3）定理描述．从表征类型和有无变式两个方面进行分析．

（4）定理论证．包括两种，一是验证，指通过直观推理对勾股定理进行论证．二是证明，指结合已知条件，运用几何性质、定理与代数运算等对勾股定理进行逻辑演绎论证．此维度仅分析小节正文，不包括“课堂练习”．

（5）定理应用．应用问题包括例题、“课堂练习”及小节正文中具有例题和“课堂练习”功能的数学活动或问题；分为解释和探究两种认知水平．

（6）定理历史．有的数学史主题不止一种功能，如华师版中的“我国古代对‘勾股弦’的约定”，即具有定理描述功能，又具有定理论证功能；但下文的论证方法是“赵爽在‘勾股圆方图注’给出的‘弦图证法’”，该主题的意图是为引出弦图，故其主要功能是定理论证．依据数学史主题主要功能划分其位置，包括4类：定理发现、定理描述、定理论证和定理应用．如华师版上述主题的位置即为定理论证．

具体分析框架见表1．

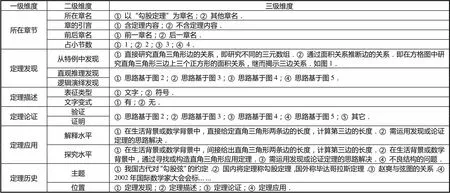
表1 “勾股定理及其应用”教材内容分析框架

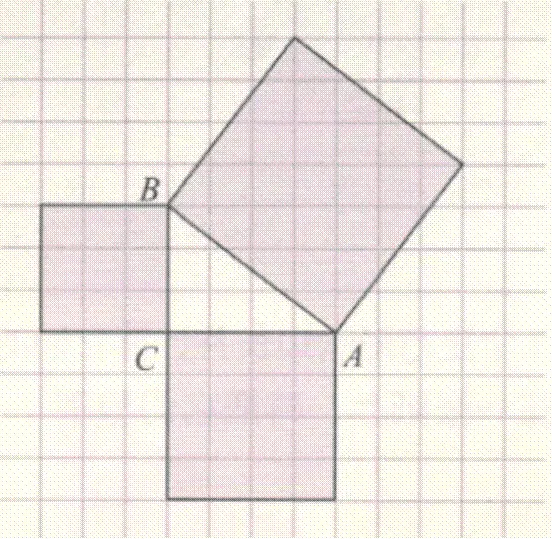
图1 通过特例发现勾股定理图

图2 发现或论证勾股定理图一

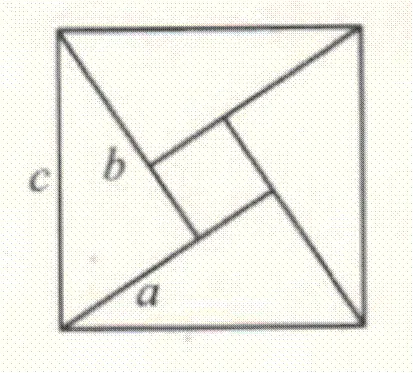
图3 发现或论证勾股定理图二

图4 发现或论证勾股定理图三

图5 发现或论证勾股定理图四

2 研究的结果与分析

2.1 所在章节

10个版本教材中，有6个版本“勾股定理及其应用”内容处于八年级上册，4个版本处于八年级下册．该内容所在章的章名有5个版本是“勾股定理”，4个版本是（特殊或直角）三角形，有一个版本是“实数”．它的前一章有“二次根式”、“轴对称”等9种数学内容，后一章有“一元一次不等式”、“实数”等6种内容．有4个版本占一小节内容，两个版本2小节，3个版本3小节，一个版本有4小节．

在“勾股定理及其应用”内容所在的册别中，10个版本教材中有4个版本的教材封面涉及勾股定理，如定理公式、赵爽弦图等．一般来说，章引言在该章教材内容中具有先行组织者的功能．有8个版本的章引言采用图形、文字等形式介绍了定理的相关内容．在教材封面或章引言中呈现勾股定理，某种程度上说明了定理在本册或本章教材数学内容中具有重要地位．

2011课标在“教材编写建议”中指出：课程内容是按照学段制定的，并未规定学习内容的呈现顺序．教材可以在不违背数学知识体系的基础上，形成自己的编排体系，体现出自身风格和特色[23]．从“勾股定理及其应用”的上述编写概况上可以看出，中国初中数学教材在该内容的编排上既具多样性，如所在章的不同前后章内容；又有一致性，如均在八年级．

2.2 定理发现

10个版本教材中，浙教版通过直观演绎发现定理，青岛版通过逻辑演绎发现定理，其它8个版本则是从特例中发现定理．在这8个版本中，仅采用思路①的版本只有北京版，仅采用思路②的是冀教版、湘教版、苏教版、人教版和上科版，华师版和北师版采用了①和②两种思路．有7个版本采用了从特例中发现定理的思路②．

传说中毕达哥拉斯最初发现勾股定理的情境是“正方形瓷砖铺地面”——等腰直角三角形及其三边上的正方形．在定理发现中，直接采用此情境的版本有华师版、冀教版、人教版，上科版和北师版则把上述情境嵌入单位方格图中．

2.3 定理描述

10个版本教材中，浙教版的定理描述处于定理发现之后，无定理论证；冀教版和湘教版的处于定理论证之后；其他7个版本的定理描述均处于定理发现与定理论证之间．针对定理的具体内容，10个版本均呈现了两种表征类型：文字和符号表征，其文字表征均以不同颜色的黑体字或附带底纹等特别方式来显示．表明这些教材较重视定理的识记．仅冀教版和湘教版在定理描述中给出了定理的文字变式，即是“已知直角三角形的两边，求第三边”；华师版在例题旁给出了定理的文字变式，北师版在节引言中有定理的文字变式．除华师版和人教版外，在定理描述中都编写有关于定理历史的内容，详见后文．

2.4 定理论证

10个版本教材中，6个版本采用了验证的论证方式，3个版本采用了证明．编写有3种论证思路的有苏教版，两种思路的4个版本，一种思路的4个版本，无论证的一个版本，共出现论证思路15次；半数版本教材呈现了两种及其以上的论证思路．然而，所有教材中的思路仅有5个种类（图形相同的验证或证明思路被视为一种论证思路）；论证思路多基于图2和图3，分别出现7次和4次．教材中的论证思路均用到了“拼图”方法，与图4和图5相比，“拼”图2和图3较易．定理发现思路中的“通过面积关系推断边的关系”，求解单位方格图中非等腰直角三角形斜边上的正方形面积时，需用到图形的“割补”方法；“拼图”和“割补”两种方法联系紧密，都暗含了“分与合”思想．7个版本中定理的发现和论证之间的这种联系便于学生经历连续的探究过程，更好地理解定理的论证思路．

赵爽曾给出两种定理证法，一种在《周髀》“半其一矩”的注文中，称其为“割补证法”，另一种是在《周髀》首章注文“勾股圆方图”中，这里称其为“弦图证法”，后者是前者的延伸[2]．“弦图证法”主要基于图3；“割补证法”指通过对图形的切割、拼接，巧妙地利用面积关系论证勾股定理，这是中国古代常用的“出入相补法”[20]．人教版采用了文中所给图之外的思路，也就是赵爽的“割补证法”．

2.5 定理应用

10个版本教材中，定理应用的问题共100道（大题中有小题，按小题个数计算）．解释水平的数学问题有46道，占46%，探究水平的问题占54%．数学学科背景的问题占63%（据分析，需运用发现或论证定理思路解决的问题情境属于数学学科背景），生活背景的数学问题占37%．“在数学学科背景中，直接给定直角三角形的两边长，求第三边长”问题占比31%，“在生活背景中，通过寻找或构造直角三角形应用勾股定理”问题占比22%，这两类问题占比较高．北师版、冀教版、人教版和苏教版编写有需运用发现或论证定理思路解决的问题，苏教版最多，有4道；此类题可以促进学生对论证思路的理解．全部版本中，仅华师版有5道不良结构的问题；编写解释性水平问题类型①时，仅华师版有一道对直角三角形直角的名称做变式的问题，即是∠=90°，其他同类型的问题均是∠=90°．不良结构问题适于不同程度的学生并利于他们探究能力的增强，变式题利于学生从多角度理解勾股定理的应用．

2.6 定理历史

10个版本教材中，定理发现中出现定理历史主题5次，定理描述中出现14次，定理论证中7次，定理应用中4次，共30次，平均每个版本出现3次定理历史．这里的论证思路均具有一定的数学史渊源，与定理论证思路出现的次数相比，定理论证中出现历史主题的次数不到它的一半，且仅有3个版本．出现次数最多的主题是“我国古代对‘勾股弦’的约定”，达8次，即是10个版本中有8个版本出现了这个主题．出现3次的主题是“国内将定理称勾股定理，国外称毕达哥拉斯定理”、“赵爽与弦图的关系”和“2002年国际数学家大会会标”．出现两次的主题是“《周髀算经》中商高对定理的观点”和“《九章算术》中的‘引葭赴岸’问题”．苏教版共出现6次数学史主题，在10个版本中最多；出现次数最少的是冀教版，仅一次．

此外，10个版本中，仅青岛版教材在小节正文中编写有数学史栏目“史海漫游”，栏目主题名称是“漫话勾股定理”．上述4类主题的分析没将该栏目包括的8个数学史主题计入其中．在数学史主题出现的38次中，国内主题出现29次，国外出现5次（四类位置中出现3次），同时具有国内外题材的主题有4次，也即是“国内将定理称勾股定理，国外称毕达哥拉斯定理”出现3次，“定理的证法多达370多种”出现一次．国内主题出现频率明显高于国外主题的频率．

3 研究的主要结论与反思

3.1 主要结论

依据上述结果，可以提炼出中国初中数学教材中勾股定理内容的主要编写特点：

（1）该内容所处的知识编排体系，即具多样性，又有一致性．

（2）7个版本采用了从特例中发现定理的思路②，即通过面积关系推断边的关系．

（3）定理描述中，全部教材强调定理识记的引导，8成注重数学史的呈现．

（4）6个版本的论证方式是验证，半数教材采用了两种及其以上的思路，但论证思路种类少且集中．

（5）定理应用的问题在认知水平和情境类型上分布较均衡，但不良结构问题的数量较少．

（6）全部版本融入了数学史，但定理论证中呈现的历史主题较少，国外的定理历史主题出现频率较低．

（7）各版本均为学生提供了积淀数学操作活动经验的素材，9个版本的教材展现了完整的定理发现、描述和论证过程．

3.2 反 思

3.2.1 完善过程性内容增强数学核心素养落实的有效性

研究结论显示，中国绝大多数初中数学教材为学生经历定理发现、描述、论证和应用的完整过程提供了良好的学习机会，较好地落实了引导学生积累数学活动经验的要求，进而可以促进学生的几何直观、推理（包括合情推理和演绎推理）能力和应用意识等数学核心素养的培育．特别地，定理发现和论证中的诸多画图、观察、计算和拼图等活动可以发展学生的几何直观．

但是，某些版本在落实核心素养方面还有提升空间，需完善有关过程性内容．在定理发现中，湘教版教材只编写了一个发现直角三角形三边上正方形面积关系的例子，没有提供变式，这对学生发现定理是不够的，可能会影响他们合情推理能力的提高．此外，可以参考一些优秀成果来优化该部分教材内容，如吴增生等通过两项“剪拼”任务引导学生“再发现”赵爽“割补证法”的做法，增强了学生“发现感”进而发展了他们的发现、提出问题与分析、解决问题的能力[4]．

2011课标在“教学建议”中指出，在第三学段中应把证明作为探索活动的自然延续和必要发展，使学生知道合情推理与演绎推理是相辅相成的两种推理形式[23]．对于定理论证，浙教版教材缺少这个过程，可能会影响学生对合情推理与演绎推理的关系的理解．为实施探究水平的教学，勾股定理在教学设计上存在一个难解的困惑：证明有难度，一般来说学生很难自行探究、寻得解决的方法[24]．多数教材尽管在定理发现和论证思路中都内隐“分与合”思想，却对此联系揭示不够，从而会导致某些教师不能发现它，设计不出解决上述困惑的探究教学，影响学生推理能力和几何直观的发展．因而建议在定理论证前增加一些提示语，如“为验证定理，你能应用探索定理中的思想方法吗？”，以增强学生对论证思路的“发现感”．此外，大多版本教材的不良结构问题的数量偏少，可能会减少学生发展应用意识和创新意识的机会．

3.2.2 适当增加论证思路的种类进一步凸显数学教材编写特色

2011课标在“课程内容”中针对“勾股定理及其应用”指出：探索勾股定理，并能运用它解决一些简单的实际问题[23]．由上述研究可知，10个版本教材对该内容的编写，在遵循课标基本要求的基础上，既有定理内容处于八年级,强调数学活动经验积累，重视定理识记，问题类型分布均衡等共性特点，又各具特色，如人教版较重视揭示勾股定理的数学史背景，苏教版较注重论证思路的多样化，华师版强调不良结构问题的设置等．

然而，教材中论证思路种类少且集中，与勾股定理的数百种证法不大相称，也失去了教材多样化的应有之义，进而对学生的数学个性发展产生不利．故建议在教材小节正文中适当增加论证思路的种类，进一步凸显各版教材编写特色．因为教材是初中农村教师发展数学知识的主要来源之一[10]，这也有利于他们丰富关于勾股定理论证思路的数学知识．

3.2.3 挖掘多元文化素材适度扩大数学史的内容范围

2011课标在“教材编写建议”中指出：数学文化作为教材的组成部分，应渗透在整套教材中．为此，教材可以适时地介绍有关背景知识，包括数学发展史的有关材料等[23]．10个版本教材均接受了此建议，并将其落实到了教材的编写中．

勾股定理曾先后在不同地区或国家被不同民族所发现，往往成为一种标志性的文化事件而载入这些地区或国家的文明史．据统计，历史上不同时代，不同国别的不同人士曾先后给出过四百多种勾股定理的证明[25]．这些人士包括数学家、艺术家、政治家、中学生、盲童等[26]．为促使学生更好地从多元文化视角看待数学，建议适度增添定理历史的国外题材．论证思路的编写中，历史主题出现的频率偏低会一定程度上削弱学生的“发现感”和对勾股定理丰富数学史内涵的体验，因而可以适度加大数学史渗透力度；特别地，建议采用合适的途径将有关中学生或盲童的定理论证方面的内容纳入其中，进而为学生提供数学学习的榜样．

[1] 项武义．几何学在文明中所扮演的角色——纪念陈省身先生的辉煌几何人生[M]．北京：高等教育出版社，2009．

[2] 蔡宗熹．千古第一定理——勾股定理[M]．北京：高等教育出版社，2009．

[3] 朱哲，张维忠．中日新数学教科书中的“勾股定理”[J]．数学教育学报，2011，20（1）：84-87．

[4] 吴增生，郑燕红，李宏彦，等．勾股定理教学实验研究——让学生真正经历勾股定理的“再发现”过程[J]．数学教育学报，2017，26（1）：50-54．

[5] 王艳青．中学数学教科书中勾股定理内容编排的演变研究（1949—2011）[D]．内蒙古师范大学，2012．

[6] 朱哲．数学教科书中勾股定理单元的编写与教学实验研究——基于“数学史融入数学课程”理念[D]．西南大学，2010．

[7] 黄荣金．变异理论下的数学课堂研究[M]．南宁：广西教育出版社，2010．

[8] 冯振举，王惠扬子．职前数学教师教学设计信念转变的个案研究——以HPM视角下的勾股定理教学为例[J]．数学教育学报，2016，25（2）：59-65．

[9] 王芳，张维忠．多元文化下的勾股定理[J]．数学教育学报，2004，13（4）：34-36．

[10] 李渺，万新才，杨田．初中农村教师数学知识状况及来源的调查研究——以勾股定理为例[J]．数学教育学报，2011，20（5）：47-51．

[11] 张倩，黄毅英．教科书研究之方法论构建[J]．课程·教材·教法，2016，（8）：41-47．

[12] 中华人民共和国教育部．教育部办公厅关于2016年中小学教学用书有关事项的通知[EB/OL]．http://www.moe.gov. cn/srcsite/A26/moe_714/201604/t20160428_241261.html.

[13] 王燕春．义务教育教科书数学（八年级上册）[M]．北京：北京出版社，2014．

[14] 马复．义务教育教科书数学（八年级上册）[M]．北京：北京师范大学出版社，2014．

[15] 杨俊英．义务教育教科书数学（八年级上册）[M]．石家庄：河北教育出版社，2013．

[16] 严士健，黄楚芳．义务教育教科书数学（八年级下册）[M]．长沙：湖南教育出版社，2015．

[17] 王建磐．义务教育教科书数学（八年级上册）[M]．上海：华东师范大学出版社，2013．

[18] 杨裕前，董林伟．义务教育教科书数学（八年级上册）[M]．南京：江苏凤凰科学技术出版社，2013．

[19] 展涛．义务教育教科书数学（八年级下册）[M]．青岛：青岛出版社，2013．

[20] 林群．义务教育教科书数学（八年级下册）[M]．北京：人民教育出版社，2013．

[21] 吴之季，苏淳．义务教育教科书数学（八年级下册）[M]．上海：上海科学技术出版社，2013．

[22] 范良火．义务教育教科书数学（八年级上册）[M]．杭州：浙江教育出版社，2013．

[23] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2012．

[24] 张奠宙，宋乃庆．数学教育概论（第三版）[M]．北京：高等教育出版社，2016．

[25] 李文林．从赵爽弦图谈起[M]．北京：高等教育出版社，2008．

[26] 汪晓勤．数学文化透视[M]．上海：上海科学技术出版社，2013．

[责任编校：周学智]

Research on Writing Features of the Content “Pythagorean Theorem” of Junior High School Mathematical Textbooks in China

SONG Yun-ming

(School of Mathematical Sciences, Guizhou Normal University, Guizhou Guian New District 550025, China)

Characteristics of textbooks and cultivating core literacy were important tasks of compiling mathematics textbooks entrusted by the times. Writing features of the content “Pythagorean Theorem” of junior high school mathematical textbooks in China had been analyzed by content analysis. Some common features were found in the 10 editions of the textbook. Moreover, they also had their own characteristics. For the shortage of teaching materials, some suggestions had been put forward: improving the content of processes in order to enhance the effectiveness of the implementation of the core quality, increasing the types of argumentation appropriately in order to further highlight writing features, mining multicultural material in order to expand the scope of the history of mathematics appropriately.

mathematical textbook; writing feature; Pythagorean Theorem; core literacy; content analysis

G423.3

A

1004–9894（2017）03–0044–05

2017–03–14

贵州省教育科学规划课题——初中数学教材中变式素材编写特点研究（2016B272）

宋运明（1980—），男，山东曹县人，副教授，教育学博士，硕士生导师，主要从事数学教材研究．