向量知识在椭圆中的渗透
2017-07-05广东省开平市教伦中学刘世洪
中学生数理化(高中版.高考数学) 2017年4期
■广东省开平市教伦中学 刘世洪
向量知识在椭圆中的渗透
■广东省开平市教伦中学 刘世洪
向量知识与圆锥曲线的交汇问题已成为高考的热点问题。在平时的学习中就应当注意并积累这一热点问题的各种解法。椭圆方程是圆锥曲线中的一种重要曲线方程,在学习椭圆时,我们就要把向量与椭圆的交汇问题作为一个重要的题型来研究与学习。
一、向量知识背景下的线段的定比分点问题在椭圆中的渗透
(Ⅰ)求椭圆方程;

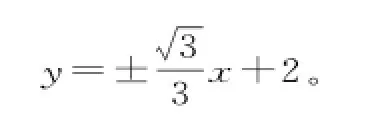
点评:题设条件中出现有向线段所成的比,实际上是告诉我们一个向量方程,如果向量方程中的向量为坐标表示,那么就为我们提供了一个求值的条件。因为未知数的求解都是要通过方程来确定,而且向量方程为我们提供的是两个代数方程,因为向量方程等号两边的向量的横、纵坐标都要相等。就像该题由向量方得(-x1,2-y1)=2(x2,y2-2),于是获得两个代数方程-x1=2x2与2-y1=2y2-4。
二、共线向量与椭圆问题的交汇

三、向量数量积在椭圆中的渗透

(责任编辑 王福华)
由②③⑤得3m2=b2。 ⑥
由④⑥解得b2=3,m=±1适合①式。
故所求直线l的方程为y=x+1或y=x-1;椭圆C的方程为
点评:若点P、Q的坐标分别为P(x1, y1),Q(x2,y2),则向量数量积的坐标表示为就像该题的题设条件一样,如果告诉我们向量数量积的值为-3,则我们就可以通过该数量积建立方程x1x2+y1y2=-3,从而为下面的求值问题创造条件。
