聚焦高考变换中的解析几何大题

■陕西省洋县中学 朱永明 刘大鸣((特级教师))

聚焦高考变换中的解析几何大题

■陕西省洋县中学 朱永明 刘大鸣((特级教师))

高考中的解析几何题,难度为中档以上,主要考查求曲线轨迹方程的方法,圆锥曲线的定义与性质应用,各圆锥曲线之间的联系,直线与圆锥曲线间的位置关系及弦长、中点弦、最值、定点、定值的探索问题等,其中直线与圆锥曲线的位置关系是考查的重点和热点,常与平面向量、函数与导数、方程、不等式等知识联系在一起,考查知识点多,运算量大,能力要求高,本文围绕如何寻找解决这种题型的技巧与捷径来展开。

聚焦1——利用“点差法”简化求解中点弦的有关问题

(1)求椭圆的标准方程;

(2)如果△BMN的重心恰好为椭圆的右焦点F,求直线l的方程。

解析：(1)由已知可得所以故椭圆的标准方程为

(2)椭圆的右焦点F(2,0)在椭圆内,满足恒相交的前提,用点差法探究。如图1,设线段MN的中点为Q(x0, y0),由三角形重心的性质知又B(0,4),所以(2,-4)= 2(x0-2,y0),得x0=3,y0=-2,求得Q的坐标为(3,-2)。设M(x1,y1),N(x2,y2),则x1+x2=6,y1+y2=-4。

图1

感悟:求中点弦方程或垂直平分线的问题时常选用“点差法”。“点差法”必须以直线和圆锥曲线相交为前提,且注意直线斜率是否存在,当不存在时要特别验证。“点差法”揭示了弦的斜率可以用弦的中点坐标来表示,在椭圆中,以P(x0,y0)为中点的弦所在直线的斜率为在双曲线中,以P(x0,y0)为中点的弦所在直线的斜率为在抛物线y2= 2px(p〉0)中,以P(x0,y0)为中点的弦所在直线的斜率为。

聚焦2——由特殊情况猜想定值,再通过检验证明一般情况

解析：①当直线l过原点时,由椭圆的对称性,可知

感悟:对于定值的探索性问题,我们可先特殊化处理,猜想问题的存在性,再作一般性的证明。这样处理能为探究提供具体的方向,减少运算量。如本题中取平行直线系恒过原点,利用P、Q重合得到使探究是定值的问题简单明朗化。

聚焦3——合理选择参变量探究曲线恒过定点问题

解析：设直线PQ的方程为y=kx,由解得交点P、Q的坐标分别为

设M(0,yM),由A、M、P三点共线,得

设N(0,yN),同理由A、N、Q三点共线,得

感悟:本题探究以MN为直径的圆是否经过定点,需要将圆的方程(含参数)写出来,然后重点求M、N两点的坐标。而M、N两点是由直线PA、QA派生出来的,我们需要先探讨P、Q的坐标。设直线PQ的方程为y=kx,通过解方程组求得各个量,引入参量k;直接设出P、Q的坐标,用参量x0,y0表示其他量,从而顺利解决问题。

聚焦4——构建两条曲线交点的曲线系方程证明直线恒过定点

在平面直角坐标系xOy中,从抛物线C:y2=4x上的点P(1,2)引斜率分别为k1、k2的两条直线l1、l2,直线l1、l2与C的异于点P的另一个交点分别为A、B,若k1k2=4,试探究:直线AB是否恒过定点?若恒过定点,请求出该定点的坐标;若不恒过定点,请说明理由。

解析：直线恒过定点的探究,建立直线系方程解出交点。设直线PA的方程为y-2= k1(x-1),直线PB的方程为y-2=k2(x-1),由整理得k1y2-4y+同理,得

因为k1k2=4,所以故所以直线AB的斜率,直线AB的方程为x-2,解出其交点为(0,-2),所以直线AB恒过定点(0,-2)。

感悟:利用题设写出已知点(或直线)的坐标(或方程),设出未知点(或直线)的坐标(或方程),此时设的变量为参量,结合已知条件求出目标曲线的含参方程。常常将含参方程化成m(k)·f(x,y)+g(x,y)=0型,令与参数式m(k)相乘的式子f(x,y)=0,且g(x,y)=0解出交点,从而证明直线恒过定点。

聚焦5——构建二元目标函数求最值

动点Q在椭圆C:2x2+y2=5上移动,两定点为A(-,1),B,-1)。求△ABQ的面积最大时点Q的坐标。

解析：设点Q(x0,y0),则有5。直线AB的方程为x+2y=0,则点Q(x0,y0)到AB的距离且则△ABQ的面积:

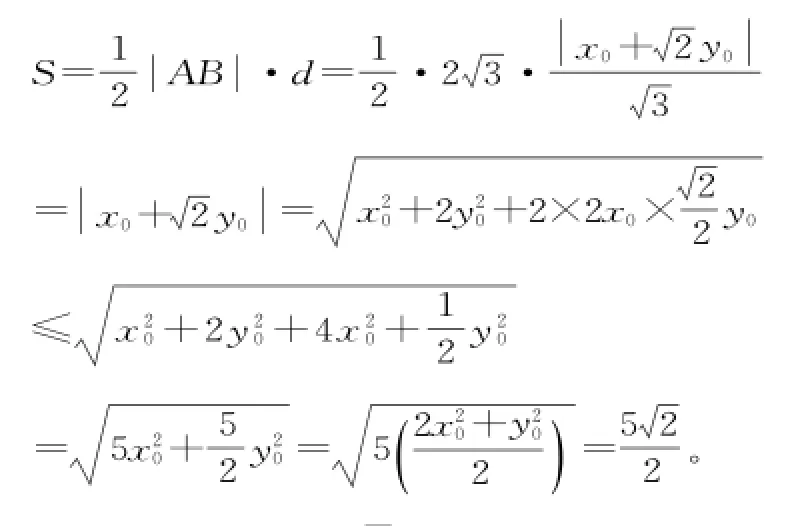
根据能力提升规律，首先通过随堂案例，进行单元知识的学习，每一/几个模块学习完成后，通过单元项目/阶段实训，进行知识的巩固和提升，课程学完之后，通过课程综合实训，完成知识的灵活运用。

感悟:设出动点Q的坐标后,将目标转化为二元函数,可以不消元,将乘积2x0y0转化为然后利用基本不等式求得△ABQ的面积的最大值,最后由2x+ y=5获得定值。

聚焦6——利用平面几何三点共线的条件求最值

图2

感悟:椭圆上的点到椭圆内一定点和一个焦点的距离之和的最小值,用定义转化为椭圆上的点到另一个焦点和椭圆内定点的距离之差的最大值,再用“两边之差小于或等于第三边”求最值,即用求解。

聚焦7——探索性问题求解中的“特殊位置猜定点”和“肯定顺推法”

图3

(1)求椭圆E的方程。

(2)当直线l与x轴平行时,设直线l与椭圆相交于C、D两点。如果存在定点Q满足条件,则。所以Q点在y轴上,可设Q点的坐标为(0,y0)。

当直线l与x轴垂直时,设直线l与椭圆相交于M、N两点,则M,解得y0=1或y0=2。

所以,若存在不同于点P的定点Q满足条件,则Q点的坐标只可能为Q(0,2)。

当直线l的斜率不存在时,由上可知,结论成立。

当直线l的斜率存在时,可设直线l的方程为y=kx+1,A、B的坐标分别为(x1, y1)、(x2,y2)。联立得(2k2+ 1)x2+4kx-2=0。其判别式Δ=16k2+ 8(2k2+1)〉0,所以因此2k。易知,点B关于y轴对称的点的坐标为B1(-x2,y2)。

感悟:圆锥曲线中的探索性问题,首先用特殊位置探究定点或定值,然后采用“肯定顺推法”进行推理。假设满足条件的几何元素或参数值存在,然后利用这些条件并结合题目的其他已知条件进行推理与计算,若不出现矛盾,就说明满足条件的几何元素或参数值存在;若在推理与计算中出现了矛盾,则说明满足条件的几何元素或参数值不存在,同时推理与计算的过程就是说明理由的过程。本题中利用斜率不存在或斜率为0探究出满足条件的特殊点Q,然后再进行推理,推理证明中用到直线和圆锥曲线位置研究的通法,特别引入对称点证明三点共线将长度比值转化为坐标的绝对值的比使问题简单化,值得借鉴。

(责任编辑 王福华)