基于ANSYS的数控铣床立柱性能分析及结构优化*

董 斌，鄢 威，张 华

(武汉科技大学 a.机械自动化学院；b.绿色制造与节能减排中心，武汉 430081)



基于ANSYS的数控铣床立柱性能
分析及结构优化*

董 斌a，鄢 威b，张 华b

(武汉科技大学 a.机械自动化学院；b.绿色制造与节能减排中心，武汉 430081)

为改善机床的力学性能，提高整机加工精度，以XK714数控铣床立柱结构为研究对象，采用ANSYS Workbench建立其有限元模型进行优化分析。其静力学分析表明立柱结构整体可靠但设计过于保守，谐响应分析发现立柱前两阶固有频率偏低。运用局部灵敏度分析获取影响立柱性能的关键尺寸，并将其作为设计变量，以立柱的质量，前两阶固有频率和最大形变量作为指标进行结构优化。最终，立柱的一二阶固有频率分别提升15.487%和13.643%，最大形变降低2.32%，并且立柱减重达到10.31%。结果表明:该设计方法可以为机床零部件的设计提供借鉴。

谐响应分析; 灵敏度分析; 结构优化

0 引言

科技的进步推动着制造业的高速发展，机床正朝着高效率、高可靠性、高柔性化和模块化的方向转变[1]。传统意义下的经验类比等设计方法已经无法满足目前机床的发展，通过模态分析、谐响应分析等方法识别出机床结构的薄弱环节，进而对机床进行响应面分析及目标驱动优化，能使机床的结构设计更加合理[2]。

作为机床的核心结构，立柱同时连接着床身和主轴箱，其强度和刚度是零件加工精度的保证，直接关系到整机的工作性能。因此，对立柱力学特性的研究具有重要现实意义[3]。

立柱通常采用薄壁多筋结构，内部形态复杂，加工受力后的应力和应变状况也较复杂。通过传统的设计方法来设计的立柱，结构中往往存在诸多不合理的地方，而优化设计方法的出现，可以设计出满足性能要求的结构方案。目前，对于机床的优化多集中在结构设计方面，包括筋板样式的设计和布局，关键零部件截面形状的改变等等。虽然可以一定程度上提升机床的性能，但是缺少对结构尺寸的整体把握和评判，优化工作量大，针对性不足。

本文以XK714数控铣床立柱结构为研究对象，以Ansys Workbench分析软件对立柱进行了力学分析，找到了其薄弱环节，然后采用响应曲面优化法，通过灵敏度分析评判尺寸因素的影响权重，进而选择关键尺寸优化改进，减少参数优化量，提升了优化效率。在减重的情况下使立柱获得较好的力学性能，为机床的结构优化提供借鉴。

1 数控铣床立柱的有限元模型

采用SolidWorks软件建立XK714数控铣床三维模型，如图1所示。并将立柱和主轴箱导入Ansys Workbench中。

图1 XK714数控铣床三维模型

由于立柱空间复杂，为防止载荷传递不准，将主轴箱和立柱主体同时建模，另外，为了确定最危险工况下立柱的强度和刚度，把主轴箱置于立柱的最顶端远离工作台处。

利用ANSYS求解后立柱的平均尺寸为25 mm，共得到26532个节点，单元数目为23821个:主轴箱平均尺寸为15 mm，共得到35621个节点，单元数目为31481个。其有限元模型如图2所示。

图2 立柱及主轴箱有限元模型

2 数控铣床立柱的静力学分析

作为结构有限元分析的基础，对机床整体和零部件进行静力学分析，可以找出系统中应力、变形量等最大的结构，为以后对薄弱环节的改进及优化提供依据[4]。

根据该铣床常用铣削方式和铣削量，对主轴箱夹持刀具的中心处施加X,Y,Z向的载荷，通过计算，其幅值大小分别为644N，1011N,1655N，另外，主轴电机和电机座的重力载荷取700N，重力加速度9806.6mm/s2。立柱与床身接触面的螺栓孔处的转动和移动均受到了限制，故采用全约束边界条件进行模拟。

通过求解，得到立柱的X,Y,Z三个方向的形变云图(图3～图5)，直观显示危险工况下立柱的强度和刚度。

图3 X向形变

图4 Y向形变

图5 Z向形变

通过上述求解得到机床X,Y,Z三个方向的变形及刚度数据如表1所示。

表1 XK714数控铣床静力学分析结果

从立柱的有限元形变图可以看出，在远离立柱与床身的联接面处变形达到最大值,并且在X和Z方向的变形量较大，刚度偏低。由于在立柱与床身联接面螺栓孔施加了全约束，该结构就相当一个悬臂梁，约束处形变最小，沿模型向上逐渐增大。因此，要降低整机的最大形变，就必须先降低立柱在X和Z方向的形变。

另外，机床的等效应力分布均匀，大部分区域在5MPa以下，最大等效应力为9.68MPa，远小于其极限应力σb=200MPa。分析表明机床结构整体是可靠的，但是安全系数太大，设计过于保守。若综合考虑立柱的刚度，强度和形变的条件下对立柱各部分尺寸进行优化设计，则可以在满足零件加工精度的同时，最大限度的减轻结构的质量，节省原材料的消耗，提高资源利用率。

3 立柱谐响应分析

谐响应分析是用于确定线性结构在承受简谐规律变化载荷稳态响应的一种方法，其目的在于计算出结构在多种激励下所产生的响应，验证设计能否克服共振、疲劳等引起的有害效果，防止共振现象的发生[5]。

在静态分析的基础上对系统进行模态分析，得出1阶固有频率90.54 Hz , 2阶固有频率为99.90Hz , 3阶固有频率为180.08Hz 。在刀具中心处施加X、Y、Z三向载荷，同时考虑模态分析前5阶主振型，将简谐力频率范围设置为0～300Hz。在此频率范围内施加简谐激励，结构的响应谱线如图6～图8所示。

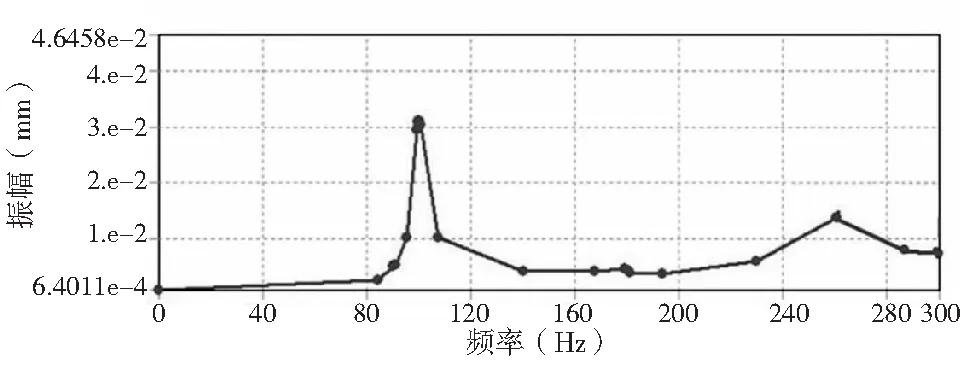
图6 X向谐响应谱线

图7 Y向谐响应谱线

图8 Z向谐响应谱线

从上图X、Y、Z各向谐响应谱线分析可知，外加激励频率为90.508 Hz时会引起Z向共振，振幅为0.47mm，一阶模态的激发方向为Z向。外加激励频率为99.86 Hz时会引起Y向共振，振幅达0. 036mm，二阶模态的激发方向为Y向。外加激励频率为99.94Hz时会引起X向共振，振幅为0.031mm，同时引起二阶模态的X向激发。考虑实际加工条件，立柱的前两阶模态易落入外加激励的范围引发共振，提高机床的抗振性应考虑提高立柱一二阶固有频率。

4 灵敏度分析及优化设计

4.1 灵敏度分析

灵敏度分析是研究系统的状态或输出变化对系统参数变化敏感程度的方法。通过灵敏度分析可以展示哪些参数对系统影响较大，并且定量计算出影响程度，能够为参数的优化做指导。

此次灵敏度分析，选取立柱的内筋板厚，外筋板厚，底板厚，内径宽，孔径和连接板宽作为参变量。立柱尺寸位置简图如图9所示，尺寸参数如表2所示。

图9 立柱尺寸位置简图

表2 立柱尺寸参数表

利用DesignExplorer中的Response Surface建立输入与输出参数间的关系。以上述6个尺寸作为变量，以立柱的最大形变量，质量以及第1、第2阶固有频率作为响应进行灵敏度分析，则各参数影响情况如图10～图13所示。

图10 质量灵敏度 图11 最大形变灵敏度

图12 1阶频率灵敏度 图13 2阶频率灵敏度

通过灵敏度分析，可以确定各因素对质量的影响主次顺序为：壁厚>底板厚>连接板宽>内筋板厚>外筋板厚>孔径;各因素对于最大形变的影响主次顺序为：壁厚>连接板宽>内筋板厚>孔径>外筋板厚>底板厚；各因素对于一二阶固有频率的影响主次顺序为：壁厚>连接板宽>外筋板厚>内筋板厚>底板厚>孔径。对各个参数灵敏度分析，为后续尺寸优化及圆整提供了参考依据。

4.2 优化模型及分析

结构优化设计是基于力学和数学规划的理论，通过计算机技术求得最优解的设计方法[6]。首先需要建立实际问题的优化数学模型，其次选择算法进行求解。

(1)设计变量

由于立柱外形尺寸由机床的规格决定，一般不宜改变，选择设计变量时，立柱外形尺寸参数不变。选取对于输出结果影响较大的X2、X3、X4、X6作为设计变量。

(2)约束条件

根据立柱设计要求，4个设计变量有尺寸的约束限制：

(3)目标函数

对立柱进行优化设计时，将其质量，最大形变量以及前两阶固有频率作为性能指标，建立相应的多目标优化函数：

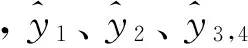
在灵敏度分析的基础上，应用Ansys中的Response Surface Optimization模块对部件进行优化。优化过程产生了3组较好的候选设计点，如表3所示。

表3 目标优化结果

由分析可知：Candidate Point 1，质量大幅减小，一阶频率可以有效避开实际工作频率，但二阶频率接近共振点，且由于部件刚度减弱，导致变形增大。Candidate Point 2，质量减幅适中，变形量变化不大，静态性能基本不变，但一二阶固有频率提升明显，有效避免共振发生。Candidate Point 3，一二阶固有频率大幅提升，变形量减小但质量增幅较大。故综合考虑，选择Candidate Point2为最优设计点。

表4 参数优化结果

5 结论

应用ANSYS有限元软件对数控铣床立柱结构进行有限元建模，通过静力学分析，发现机床Z向和X向形变较大，安全系数太高，设计过于保守，经谐响应分析，发现机床的一二阶固有频率偏低。基于localsensitivity分析，获得影响机床性能的关键尺寸，并将其定义为设计变量，将质量，前两阶固有频率和最大形变作为优化目标，对立柱进行尺寸优化，对优化产生的3组候选设计点综合分析，选取Candidatepoint2作为最优结果。此次优化，立柱前两阶固有频率分别提升15.487%和13.643%，最大形变降低2.32%，质量减少10.31%。结果表明，优化效果良好，该方法能够为机床设计提供参考。

[1] 王泽林.机床滑动结合而特征参数识别分析与研究[D].北京:北京工业大学，2011.

[2]张疆平，李想，贾成阁，等. 基于灵敏度分析的XK719数控铣床尺寸优化设[J]. 组合机床和自动化加工技术，2016(2)：5-8.

[3]陈庆堂. 基于ANSYS的数控铣床立柱结构分析及参数优化设计[J]. 郑州轻工业学院学报，2010,25(5):105-108.

[4]张洪信.有限元基础理论与ANSYS应用[M].北京:机械工业出版社，2006.

[5]商跃进.有限元原理与ANSYS应用指南[M].北京:清华大学出版社，2005.

[6]梁醒培，王辉.基于有限元法的结构优化设计:原理与工程应用[M].北京:清华大学出版社，2010.

(编辑 李秀敏)

Performance Analysis and Structure Optimization of CNC Milling Machine Based on Ansys

DONG Bina,YAN Weib,ZHANG Huab

(a.College of Machinery and Automation;b. Research Center of Green Manufacturing and Energy-saving & Emission Reduction Technology, Wuhan University of Science and Technology,Wuhan 430081, China)

In order to improve the mechanical property of machine tool and enhance its machining accuracy, the stand column structure of XK714 CNC milling machine was used as research object, and a finite element model was built by ANSYS Workbench to make optimization.The static analysis results showed that the machine structure was reliable but too conservative. On the basis of the harmonic response analysis on the milling machine, it was concluded that the first and second natural frequency was low. Using local sensitivity analysis, the key dimensions which might have an influence on the performance of the stand column were found. Structure optimization was carried out where the key dimensions were used as design variables, the mass, the first and second natural frequency and the maximum strain were designed as goals. Finally, the first and the second natural frequency was improved by 15.487% and 13.643% respectively, the maximum strain was reduced by 2.32%, and the mass of the stand column was reduced by 10.31%. The results showed that the design method provided a reference for the design of parts and components of milling machine.

harmonic response analysis;sensitivity analysis;structure optimization

1001-2265(2017)06-0022-04

10.13462/j.cnki.mmtamt.2017.06.006

2016-08-29；

2016-10-10

国家自然科学基金项目(51275365)；国家863基金项目(2014AA041504)；国家科技支撑计划项目(2011BAF11B01)

董斌(1990—)，男，湖北襄阳人，武汉科技大学硕士研究生，研究方向为绿色制造，(E-mail)db_WUST@163.com。

TH166;TG659

A