数控机床立柱力学特性分析

刘建平，毕根凤

（航天科工惯性技术有限公司，北京 100074）

数控机床由于自身的激励产生振动，而产生的振动也影响着设备的精度，给相关人员操作带来困难。为了使重型机床在加工过程中保证其加工质量，因此，对重型机床立柱进行动态特性研究具有重要意义。

针对机床立柱国内学者做了大量的研究，姬宇等基于Solidworks 对机床立柱关键特性尺寸参数和立柱内部加强肋板的结构设计进行了相应的研究。方浩等通过计算得到各设计参数对立柱动态性能的灵敏度值,选择其中灵敏度值大的设计参数为设计变量。以一阶模态频率为目标,使用响应面法进行优化设计。李德刚等通过建立立柱三维模型及有限元模型,对立柱结构进行静态分析考察立柱变形趋势，通过改变立柱内部筋板结构提高立柱刚度。杨明亚等建立立柱的三维有限元模型,利用大型有限元分析软件ANSYS 对立柱部件进行了模态分析,得出了立柱前五阶固有频率和振型。安晓卫等研究了立柱承受最大切削力时，应用结构分析软件 Super SAP 对其进行了静刚度计算。上述研究学者主要从静、动特性方面入手开展的立柱相关研究，然而，上述研究缺少对机床立柱剪力的统一数学模型，这更突显出本文研究的必要性。

1 数控机床立柱受力图

1.1 立柱等效载荷

数控机床立柱下端与其滑座固定，其约束条件可视为一端约束，一端自由。论文分析立柱在启动载荷作用下的强度计算，因此，机床立柱受机床惯性力作用，另外，在计算过程中需要将其他构件的载荷等效到机床立柱上，因此，存在弯矩作用。立柱总体受力图如图1 所示。

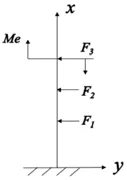
图 1数控机床立柱等效载荷图

图1 中，F1为立柱本身在运动过程中所受到的惯性力；F2是横梁作用在立柱上的惯性力；F3是连接梁作用在立柱上的惯性力；Me 是连接梁等效到立柱上的弯矩。

1.2 立柱剪力分布

依据受力分析图可确定其剪力和弯矩图如图2、图3。

如图3 所示，可以观察到立柱的底部受到的剪力最大，立柱质心处受到的剪力次之，与横梁连接处受到的剪力较小，与连接梁连接处受到的剪力最小。

1.3 立柱弯矩分布

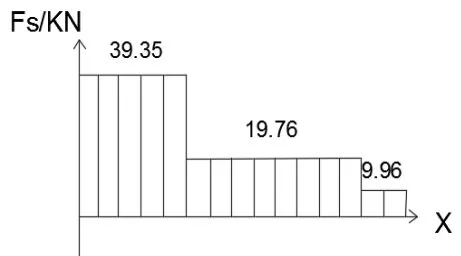
图2 立柱剪力图

图3 立柱弯矩图

如图3 所示，可以观察到立柱的底部受到的弯矩最大，立柱质心处受到的弯矩次之，与横梁连接处受到的弯矩较小，与连接梁连接处受到的弯矩最小。

2 截面形心计算

为了实现数控机床立柱截面的惯性矩计算，首先要获取惯性轴的位置，因此根据材料力学相关知识可知，立柱截面的型心公式为：

立柱截面图形如图4 所示。

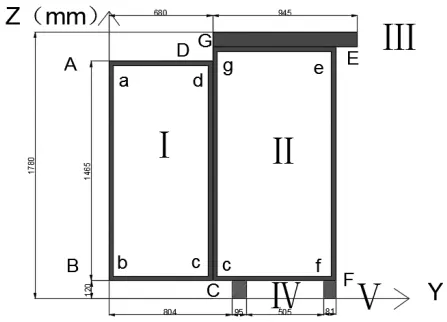
图4 立柱截面图

由于立柱的截面图形是不规则的图形，因此我们可以把该截面图形看成由若干简单图形组成。在这里，我们把这个截面由图中5 个矩形Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ拼接而成。选取坐标系如上图所示。每个矩形的面积及形心位置分别为：

根据公式（1）求出立柱整个截面图形形心C 的坐标为

3 截面计算惯性矩

形心位置确定后，使用平行移轴公式，分别算出矩形Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ对zc 轴的惯性矩。

矩形Ⅰ：

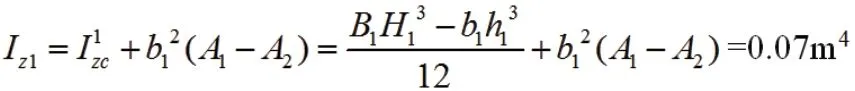
矩形Ⅱ：

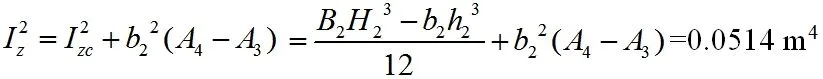
因此，整个图形对z 轴的惯性矩为

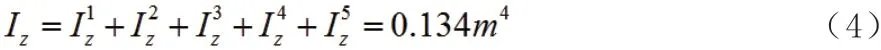
4 强度校核

如图4 弯矩图可以看出立柱底部受到的弯矩最大，且最大值为MMAX=216.11kN·m。

由于该图形截面对中性轴不对称，同一截面上的最大拉应力和压应力并不相等，计算最大弯曲正应力时，应以y1和 y2 分别代入式（5）。在该截面弯矩是负的，最大拉应力在上边缘各点其值为：

5 有限元分析验证

通过在UG 中建立立柱的集合模型，应用ANSYS 软件对立柱开展有限元分析，按照立柱模型的边界条件对立柱施加载荷和约束，最终获得立柱的应力状态云图，通过对比可知，理论和仿真结果误差率为7.8%，其理论值精度较高。

图5 立柱有限元仿真云图

6 结语

论文以数控机床立柱为研究对象，考虑立柱在冲击载荷作用下的受力分析，将工况载荷转化成等效载荷作用于立柱上，从而建立数控机床立柱的力学模型，针对立柱均匀截面的特性，开展了立柱的截面型心计算，然后以通过型心得轴为惯性轴，计算立柱惯性矩，通过惯性矩的计算最终获得立柱的最大应力值，从而完成立柱的强度校核，论文最后对比了有限元仿真结果与理论结果，更直接地证明了理论模型的正确性，为数控机床的立柱设计提供了理论基础。