一种内容自适应的硬判决量化算法

王鸿奎,李瑞阳,殷海兵

(中国计量大学 信息工程学院,浙江 杭州 310018)

一种内容自适应的硬判决量化算法

王鸿奎,李瑞阳,殷海兵

(中国计量大学 信息工程学院,浙江 杭州 310018)

在视频编码器中,软判决量化可获得最优编码性能,但其中维特比算法会导致严重的系数间串行处理依赖.比较而言,基于死区的硬判决量化算法率失真性能有所损失,但不存在系数间依赖,且非常适合硬件并行流水处理.今采用离线统计的方法,分析余弦变换系数的分布情况,量化余数对量化的具体影响,构建了基于余弦变换系数分布参数,量化余数的自适应偏移模型.基于该模型提出一种内容自适应的硬判决量化算法.仿真结果表明,该算法在保证并行化处理的条件下,其编码性能相比于传统的硬判决量化有一定的提升,可接近软判决量化算法性能.

视频编码;软判决量化;率失真优化;硬判决量化

在H.26x和MPEG-x等混合框架视频编码器中,量化扮演着非常重要角色,它直接决定量化失真和编码码率消耗.在早期视频编解码器中,对余弦变换(Discrete Cosine Transform,DCT)系数大多采用均匀标量量化(Uniform Scalar Quantization,USQ).后来,MPEG-4和H.264/AVC等标准采用基于deadzone死区的均匀标量量化(Uniform Scalar Quantization With Deadzone,USQ+DZ).在USQ+DZ中,利用熵编码的统计特性,根据预测模式的不同采用不同的偏移量,相比于简单的USQ算法,使得数据压缩性能有了巨大的提升.类似于USQ以及USQ+DZ,系数独立、基于四舍五入的量化算法统称为硬判决量化(Hard Decision Quantization,HDQ)算法.HDQ算法,因不考虑系数间的相关性,适合硬件的并行处理,H.264/AVC以及最新视频编码标准HEVC中的量化均采用了基于死区的HDQ算法.

相比于HDQ算法,考虑系数间相关性的软判决量化算法(Soft Decision Quantization,SDQ)可获得更加优异的率失真(Rate Distortion,RD)性能.SDQ算法采用维特比网格搜索[1],从多个候选较优量化结果中抉择出率失真代价最小的量化候选值,从而实现率失真性能的较大提升.基于维特比的SDQ算法已被应用于H.263+及H.264/AVC标准编码器[1-2].这类方法需要在整个网格图中进行维特比网格搜索,实现动态规划优化,但计算消耗太大且复杂度太高.为了解决这一问题,提出了SDQ算法的简化算法,即率失真优化量化(Rate Distortion Optimized Quantization,RDOQ)算法.相比于SDQ算法的全网格搜索,RDOQ只搜索了部分路径,在RD性能上比SDQ算法稍差,但可大幅降低算法复杂度.因此,在H.264/AVC及HEVC等标准参考软件JM和HM中,均采用了该算法作为量化算法的备选算法.但是,RDOQ算法在抉择最佳量化结果的过程使得该算法仍有较高的复杂度.同时,上下文自适应算术编码(Context Adaptive Binary Arithmetic Coding,CABAC)面临严重的串行依赖,包括语法元素之间以及比特之间的串行处理、上下文概率状态选择与转换等.系数间的串行依赖严重阻碍RDOQ算法在硬件架构上的有效实现.

因此,本文研究DCT系数的统计特性,模拟SDQ算法,在离线模式下,构建自适应死区偏移模型.提出一种基于该模型的硬判决量化算法,以提高硬判决量化算法的RD性能.

1 背景及问题法

1.1 HDQ和SDQ量化判决

在早期视频压缩算法中,基于无记忆信源的假设,量化幅值取决于量化步长以及信号强度.编码器采用的量化算法大都为HDQ算法,如早期编码器中采用的USQ算法.随着研究的深入,理想的标量量化器应该采用非线性量化,也就是每个量化区间的间距应该不相等,每个量化区间的划分取决于信号的概率密度分布函数.而DCT系数的分布近似认为服从拉普拉斯分布[3],根据这个概率分布函数,确定非线性标量量化.研究表明,DCT系数主要分布在零频率分量附近,偏移零频率分量,出现概率呈指数下降,如拉普拉斯分布.基于这样的分布特点,有学者提出了失真最小的基于死区的均匀阈值量化(Uniform Threshold Quantization,Deadzone+UTQ)的量化方案[3].其本质是在零频率分量附近增加一个偏移量,让更多的DCT系数被量化为零,而其他部分采用均匀量化.基于死区的HDQ算法如图1及式(1)所示,范围(-T,T)即为deadzone死区,在此范围中的DCT系数经量化后的量化幅值均为零.δ为量化偏移量,且满足T+δ×q=q.

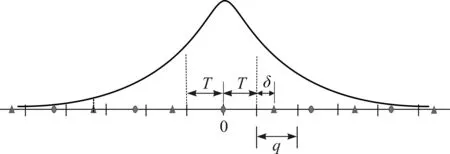
图1 HDQ量化示意图Figure 1 Schematic diagram of HDQ quantization

(1)

式中:u—DCT变换系数;q—量化步长;δ—deadzone偏移量;‖—求绝对值操作;floor—向下取整操作;HDQ(u)—硬判决量化幅值.在USQ中,偏移量δ的取值为1/2.有学者在基于熵编码的统计特性的研究中,提出帧内、帧间预测模式分别采用固定死区量化偏移量1/3和1/6[3].H.264和H.265标准参考代码JM和HM中都采用该算法[3],即本文所提的采用固定偏移量的HDQ算法.相比于USQ,该算法的RD性能有了极大的提升.但该算法未能实现量化偏移量的自适应调节,也未考虑系数间的相关特性,因此,采用固定偏移量的HDQ算法有一定优化空间,相比于SDQ算法,RD性能有仍有较大的损失[4].本文的着眼点即在采用自适应死区偏移量,进一步提升HDQ算法的RD性能乃至逼近SDQ的算法性能.

在支持CABAC编码的量化算法中,由于采用有记忆信源上下文高阶熵编码,使得变换系数量化幅度不仅与块内前面已量化系数的量化幅值相关,同时会影响到块内后续变换系数的量化结果,即系数间存在着前后相关性[5].因此,需要在考虑系数相关性的条件下,兼顾编码码率消耗和编码失真,实现系数级精细量化.最优SDQ算法采用维特比搜索的动态规划方法,穷尽比较系数之间的复杂相关性[5-6].一个变换块中包含有多个串行扫描的变换系数,每个系数构成维特比网格图上一个阶点[5].维特比搜索算法中每个系数对应一个阶,每个系数有多个候选较优量化结果供选择,这些候选量化结果构成候选上下文状态.块内的串行系数(阶)以及候选量化结果(状态)构成了完整网格图,SDQ算法的核心是如何在网格图中找到编码率失真代价最小路径.最优路径由多个相邻的分支路径组成,每个阶保留一条剩存分支路径.SDQ算法可获得优越的编码性能,能实现6%～8%的码率节省[1-2],但这种性能提升是以维特比算法及CABAC编码导致高度串行依赖为代价的[7].

RDOQ算法作为SDQ算法的简化版[8-9],通过减少搜索路径,以微小的性能损失为代价,一定程度上降低了软判决的复杂度；但是,系数级上下文导致硬件流水效率不高的问题依然没有得到有效的解决[9].

1.2 软硬判决分析

在研究变换系数分布特性的基础上,提出的采用固定死区的HDQ算法,有效地提升编码器的率失真性能.一般认为变换系数服从拉普拉斯分布,其概率密度函数如下:

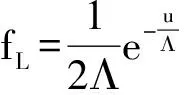
其中

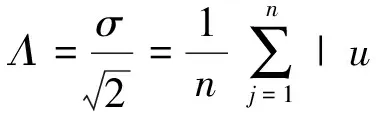
(2)

式(2)中,Λ为变换系数分布模型参数,σ为系数的标准差.u为DCT系数.在基于拉普拉斯分布模型中,采用率失真优化确定HDQ算法中的死区偏移量δ公式如下[3]:

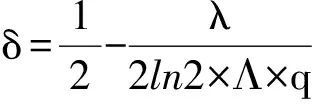
(3)

式(3)中：λ—拉格朗日乘子,在率失真约束条件下,拉格朗日乘子的表述如下:

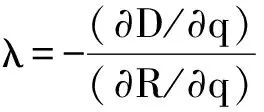
(4)

式(4)中:D—失真,R—码率,在此条件下,推导出拉格朗日系数λ的具体表述:

λ=ln2×((q-δ)2-δ2)/q.

(5)

此处存在一个“蛋鸡悖论”问题,根据式(3)和式(5),参数λ和δ是相互依赖的.而且,解决该悖论问题相对比较困难.

1 080 p序列的4×4变换块各频率分量的Λ值分布散点图如图2,不同频率分量的DCT系数的分布参数相差极大.因此,不同频率分量的变换系数在量化时偏移值的取值应该是自适应的,且不能按照式(3)的推导直接得到自适应的偏移量.

深入研究软硬判决量化机理,当HDQ算法未能逼近SDQ算法最优量化行为时,两者的量化幅度结果将会不一致,即HDQ(u)≠SDQ(u).在这些样本中,本文发现HDQ(u)=SDQ(u)+1的概率非常接近于1.这种现象可解释为:在SDQ算法中,将量化幅度减小1,失真虽有所增加,但可以大大节省码率,从而降低率失真代价.该问题的具体表述如式(6).其中量化余数ξ=mod(|u|,q)/q,mod表示取余操作.软硬判决量化结果统计图如图3,f表示频数.

HDQ(ξ+δ)=floor(ξ+δ)=1;

SDQ(ξ+δ)=floor(ξ+δ)=0.

(6)

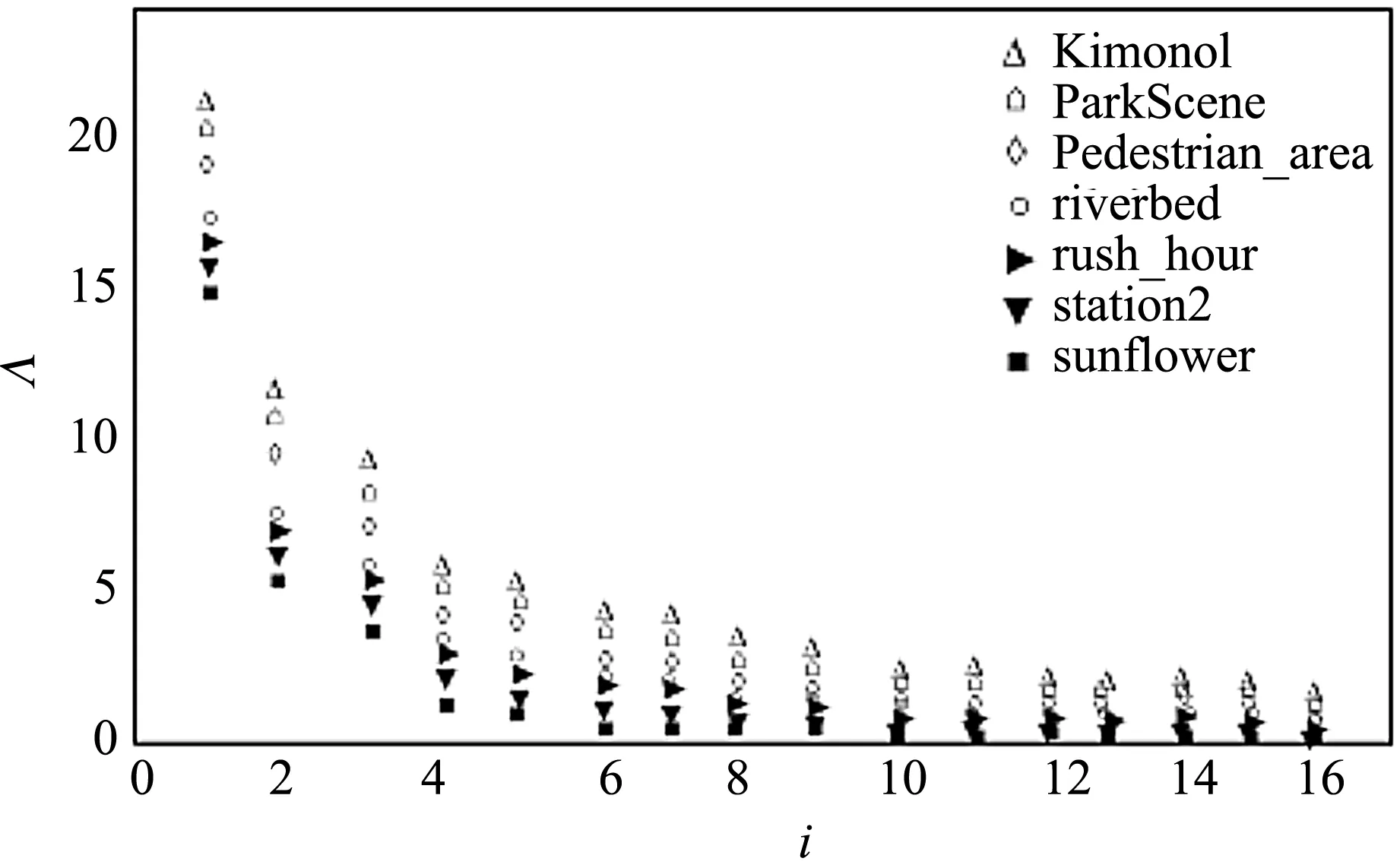
图2 DCT系数分布参数取值散点图Figure 2 Scatter diagram of DCT coefficients distribution parameters

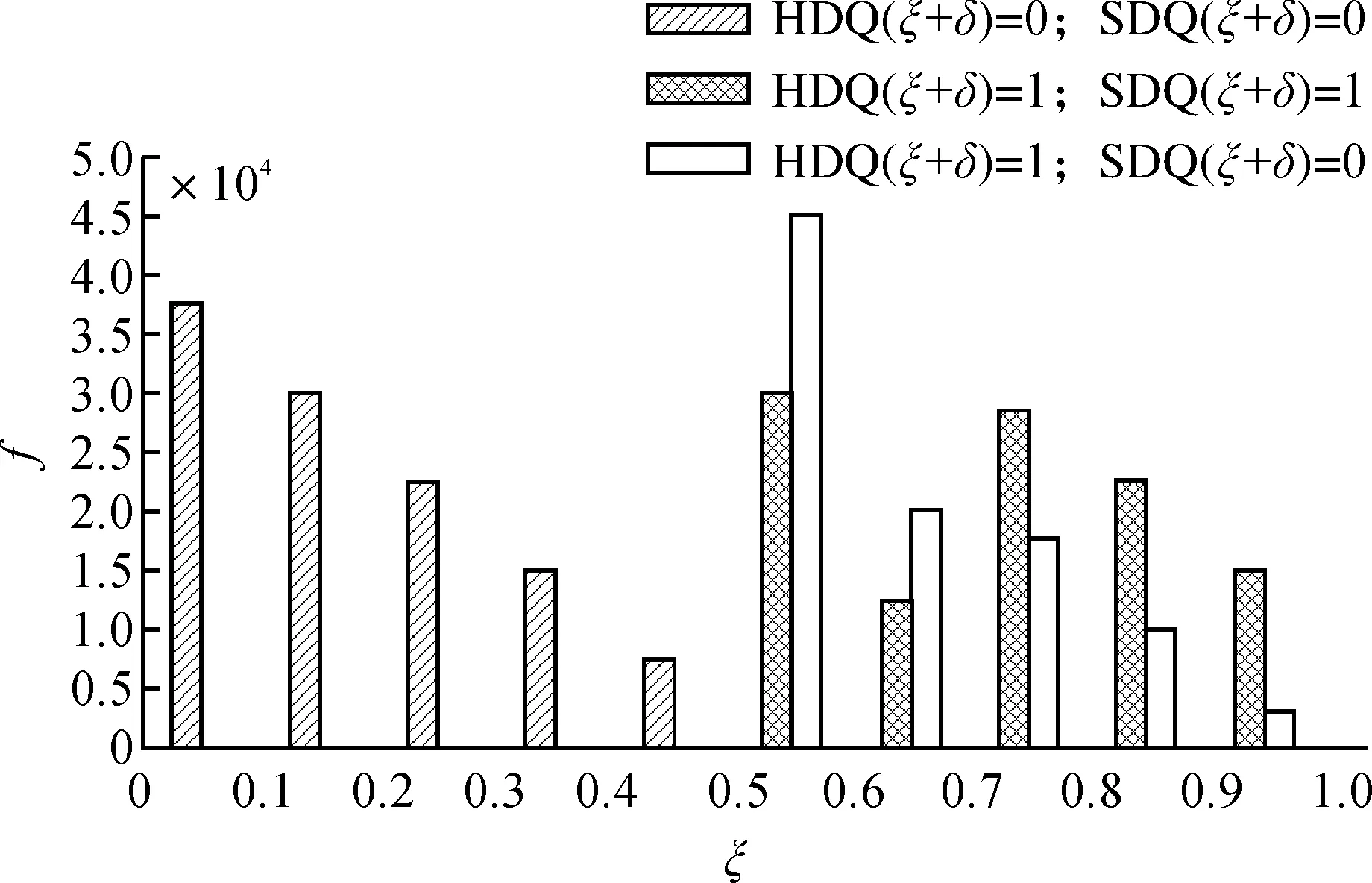
图3 软硬判决量化结果Figure 3 Results of soft and hard decision quantization

2 基于自适应偏移量HDQ算法

2.1 启发式自适应建模

本文尝试构建基于DCT分布参数以及量化余数的自适应死区偏移模型.模拟SDQ算法的数据特征和作用机理,基于统计分析方法在最大正判概率约束下,针对DCT系数分布参数、量化余数的不同组合,探索最优死区量化偏移量,离线构建参数自适应模型.

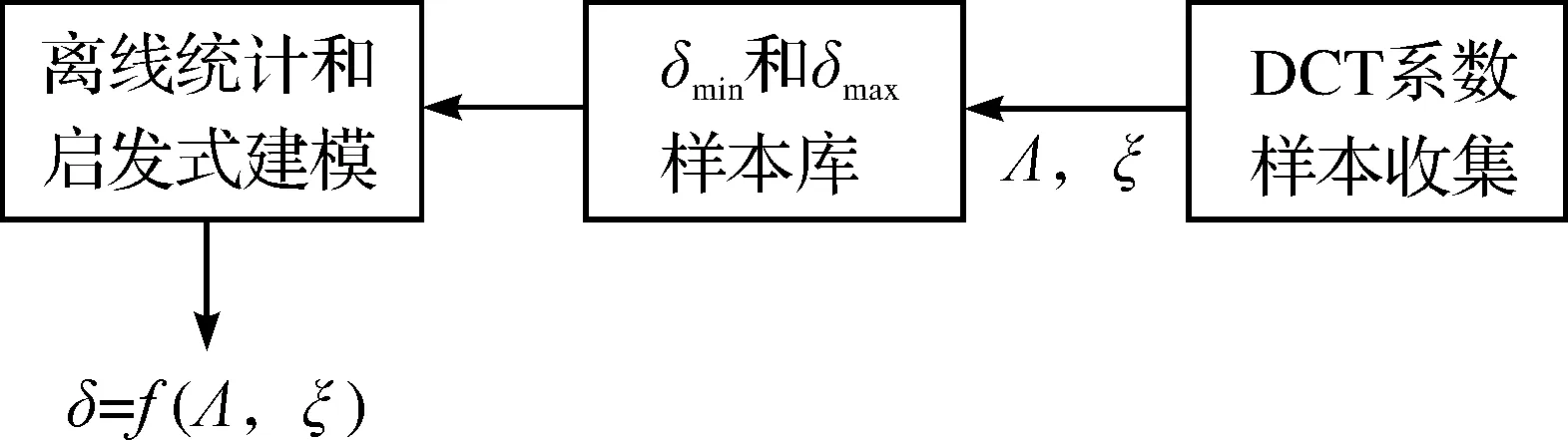
图4 自适应偏移量模型建模示意图Figure 4 Schematic diagram of adaptive offset model

本文采用的启发式模型推导方法如图4所示.首先,收集图中的DCT系数样本,DCT系数样本指的是两种量化算法(HDQ和SDQ)的量化幅值不一致情况下的DCT系数.在DCT系数分布参数以及量化余数的不同组合下,收集这些样本数据,在保证样本两种量化算法结果一致的前提下,得到所有DCT系数样本偏移量的取值范围(δmin,δmax).然后,在DCT系数分布参数以及量化余数的所有组合下,统计各组合下样本偏移量取值范围,在最大正判概率约束下,从中抉择出最佳偏移量.最终离线构建自适应偏移量模型.

2.2 最佳偏移量统计分析

死区偏移量最大取值范围为(0,1),在此范围中,存在子区间,使得采用该区间范围中的偏移量硬判决量化结果与软决量化结果一致.具体表述如下:

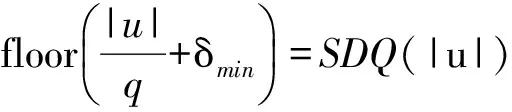
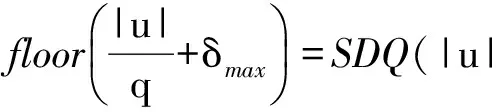
(7)

将死区偏移量的最大范围均匀划分为N个非常小的子区间,如N取500,对所有样本偏移量可取的实际范围(δmin,δmax)划分子区间进行柱状图统计分析.统计各个子区间的样本发生次数θ(k),如果第k个子区间在(δmin,δmax)范围内,那么该子区间统计值θ(k)加η(k),η(k)以及直方图表述如下:

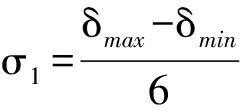
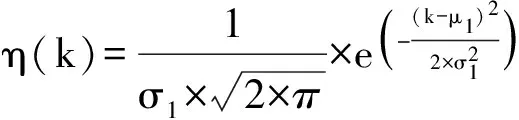
(8)

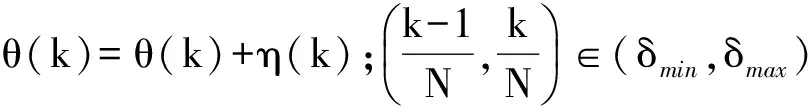
(9)

针对DCT系数分布参数Λ、量化余数ξ,得到样本最佳偏移量分段直方图结果.4×4变换块中16个样本分量在不考虑量化余数的条件下,最佳偏移量的分布情况如图5.基于DCT分布参数,量化余数构建的模型如图6.

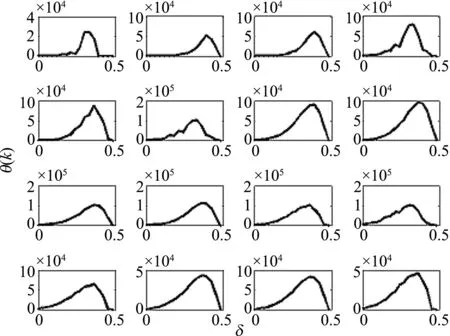
图5 偏移量δ分布直方图θ(k)Figure 5 Offset distribution histogram

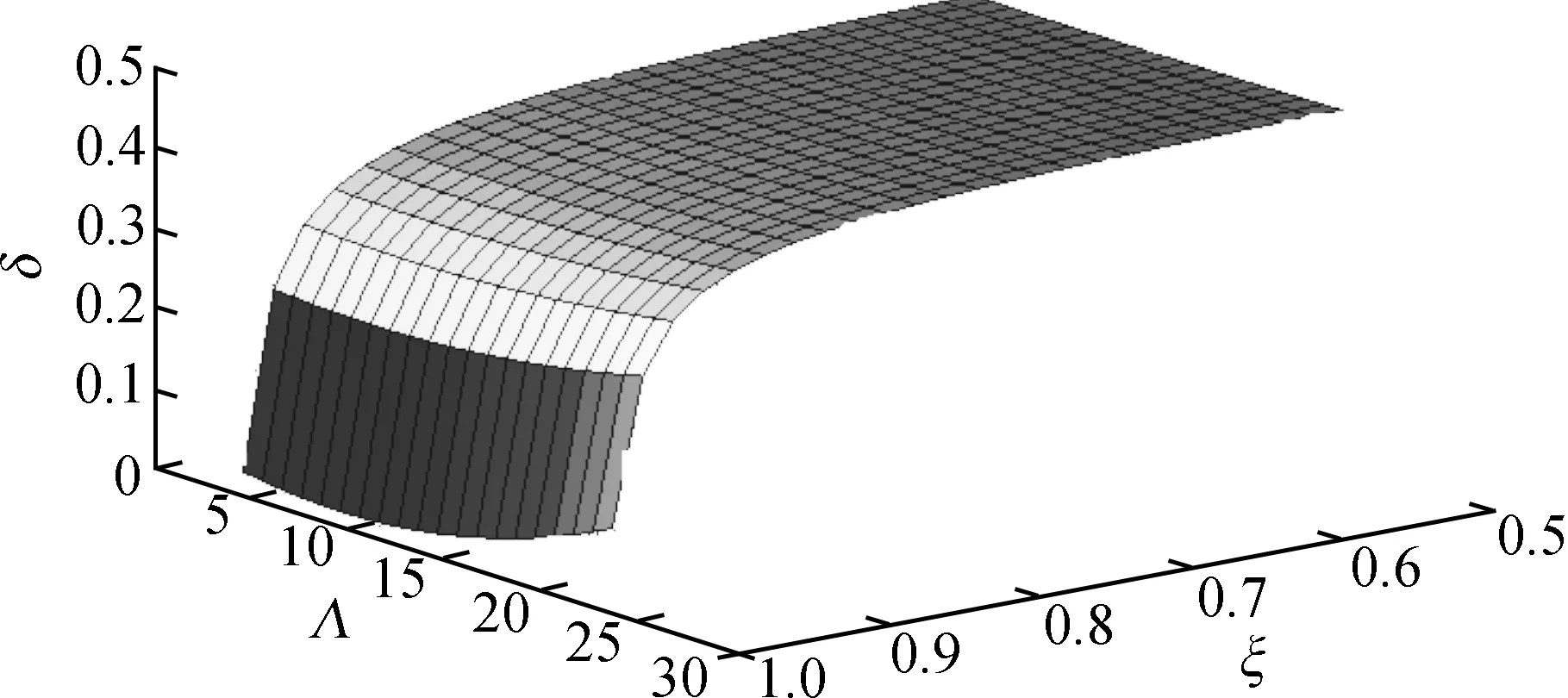
图6 偏移量δ模型图Figure 6 Offset model diagram

本文通过模拟SDQ算法机理,在率失真约束条件下,离线构建基于视频内容而自适应的偏移模型.在实际编码过程中,自适应量化算法将针对不同的视频内容,不同的压缩效果而自适应采用不同的量化偏移量,从而实现自适应量化.并且自适应量化算法在几乎不增加额外编码复杂度的前提下,可保证硬判决并行化优势,提高量化正判概率,提升算法的率失真性能.

3 实验结果

本文将提出的自适应偏移量模型可应用于H.264和H.265标准编码器,进行HDQ算法验证,并且与固定偏移量HDQ算法及SDQ算法进行了率失真性能比较.所有量化算法都同时应用于最终模式编码以及率失真优化模式选择回路中.仿真采用D1、720 p和1 080 p格式视频序列;关闭码率控制,量化参数选择22,27,32,37,覆盖低、中和高比特率应用.GOP结构采用IPBBPBB.测试编码帧数为100帧.采用主流的BD-PSNR及BD-RATE参数进行率失真性能比较[11].见表1.

表1 固定偏移量HDQ、基于本文自适应偏移量模型HDQ与SDQ算法性能对比

D1格式Interview序列的率失真性能算法对比如图7所示,图中对比了SDQ算法、固定偏移量HDQ算法以及本文自适应偏移量HDQ算法.此外,表1给出了不同测试序列的BD-PSNR及BD-RATE参数[11].根据表1结果,高分辨率视频序列情况下,本文算法有相对较高的率失真性能提升.针对1080p视频序列,实验结果表明本文算法比最佳SDQ算法和BD-PSNR仅有0.025性能损失,BD-RATE平均有1.121%码率增加.此外,相比于固定偏移量HDQ算法,本文算法BD-PSNR平均有0.099 dB性能提升,BD-RATE平均可节省3.340%码率.可见,本文提出的算法率失真性能上明显优于固定偏移量HDQ算法,且十分接近最佳SDQ算法性能.计算复杂度方面,相比于固定偏移量HDQ算法,本文算法的额外计算是DCT系数分布参数,总体而言,额外增加的计算复杂度基本可以忽略,通过对比编码时间对比算法复杂度,如表2.

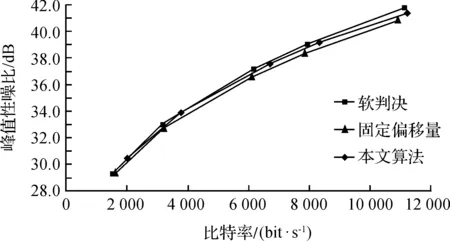
图7 典型测试序列率失真曲线示意图Figure 7 Comparison of the RD performance of the proposed, fixed-offset HDQ, and the SDQ algorithm.

表2 固定偏移量HDQ、基于本文自适应偏移量模型HDQ与SDQ算法编码时间对比

4 结 语

算法内在的串行依赖阻碍了SDQ算法硬件并发流水有效实现.HDQ算法相较于SDQ算法,编码率失真性能有显著的损失.基于统计分析及启发式建模,本文根据DCT系数分布参数以及量化余数参数,构建了自适应死区偏移量模型,并基于此提出一种内容自适应偏移量死区量化算法.实验仿真结果表明,在保持HDQ算法系数级并发处理优势的前提下,本文算法可减少传统死区HDQ算法和SDQ算法之间性能差距.

[1] WEN J, LUTTRELL M, VILLASENOR J. Trellis-based R-D optimal quantization in H.263+[J].IEEE Transactions o Image Processing A Publication of the IEEE Signal Processing Society,2000,9(8):1431-1436.

[2] YANG E H, YU X. Rate Distortion Optimization of H.264 with Main Profile Compatibility[C]//IEEE International Symposium on Information Theory. Seattle, Washington: IEEE,2006:282-286.

[3] SULLIVAN G J. Efficient scalar quantization of exponential and Laplacian random variables[J].IEEE Transactions on Information Theory,1996,42(5):1365-1374.

[4] YIN H B, YANG E H, YU X, et al. Fast soft decision quantization with adaptive preselection and dynamic Trellis Graph[J].IEEE Transactions on Circuits & Systems for Video Technology,2014,25(8):1362-1375.

[5] SUN J, DUAN Y, LI J, et al. Rate-distortion dnalysis of dead-done plus uniform threshold scalar quantization and its application-Part II: Two-pass VBR coding for H.264/AVC[J].IEEE Transactions on Image Processing,2013,22(1):202-214.

[6] 谭晶晶,殷海兵.基于HVS和时域感知失真的感兴趣区域搜索[J].中国计量学院学报,2013,24(1):55-59. TAN J J, YIN H B. Region of interest detection based on HVS and time domain perceptual distortion[J].Journal of China University of Metrology,2013,24(1):55-59.

[7] 孙俊.流媒体编码传输中若干关键技术的研究[R].北京:北京大学博士后研究工作报告,2016. SUN J. Research on some key technologies of treaming media coding and transmission[R].Beijing: Postdoctoral Research Report of Peking University,2016.

[8] KARCZEWICZ M, YE Y, CHONG I. ITU-T SG16/Q.6.Rate distortion optimized quantization[S].Antalya:IEEE,2008.

[9] HUANG T Y, CHEN H H. Efficient quantization based on rate-distortion optimization for video coding[J].IEEE Transactions on Circuits and Systems for Video Technology,2016,26(6):1099-1106.

[10] LEE H, YANG S, PARK Y, et al. Fast quantization method with simplified rate-distortion optimized quantization for HEVC encoder[J].IEEE Transactions on Circuits & Systems for Video Technology,2015,26(1):1109-1121.

[11] BJONTEGAARD G. Calculation of average PSNR differences between RD-Curves[C]//13th video coding experts group (VCEG) meeting.TX, USA:IEEE,2001:1022-1034.

A content-adaptive hard-decision quantization algorithm

WANG Hongkui, LI Ruiyang, YIN Haibing

(College of Information Engineering, China Jiliang University, Hangzhou 310018, China)

In video encoders, the soft-decision quantization (SDQ) achieves superior coding performance, but suffers from deadly sequential processing dependency. Comparatively, the deadzone hard-decision quantization (HDQ) is dependency-free and suitable for hardwired parallel processing, but suffers from non-negligible coding performance degradation. In this paper, a content-adaptive HDQ algorithm is proposed. Simulation results show that the coding performance of the adaptive HDQ algorithm is close to the SDQ algorithm.

video coding; soft decision quantization; rate distortion optimization; hard decision quantization

2096-2835(2017)02-0241-06

10.3969/j.issn.2096-2835.2017.02.017

2016-11-10 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.61572449).

王鸿奎(1990- ),男,浙江省淳安人,硕士研究生,主要研究方向为视频编码算法.E-mail:1550661343@qq.com通信联系人：殷海兵,男,教授.E-mail:yinhb@cjlu.edu.cn

TN919

A