燃料电池车用超高速空压机临界转速分析与提高措施

詹 剑，张智明，张娟楠，李昌昊，倪 玥

(1.同济大学 汽车学院，上海 201804； 2.同济大学 新能源汽车工程中心，上海 201804；3.同济大学 物理科学与工程学院，上海 200092)

燃料电池车用超高速空压机临界转速分析与提高措施

詹 剑1,2，张智明1,2，张娟楠3，李昌昊1,2，倪 玥1,2

(1.同济大学 汽车学院，上海 201804； 2.同济大学 新能源汽车工程中心，上海 201804；3.同济大学 物理科学与工程学院，上海 200092)

针对空压机进气增压可提高大功率燃料电池发动机性能和功率密度，但空压机超高速电机转子-轴承系统存在共振失稳乃至断轴的实际工程问题.本文采用有限元法建立空压机高速电机轴承-转子系统动力学模型，基于ANSYS软件对某超高速永磁电机转子进行动力学仿真，分析某燃料电池空压机高速电机转子-轴承系统的临界转速，揭示轴承刚度、轴承位置以及转轴质量等因素对临界转速的影响规律，并提出改善措施.结果显示，增大轴承刚度、适当减小轴承跨距以及减轻转轴的质量可以有效地增加转子轴承系统的临界转速.

燃料电池空压机；高速转子-轴承系统；转子动力学；临界转速

燃料电池是一种将氢和氧的化学能通过电化学反应直接转换为电能的能量转换装置，其能量转换效率不受“卡诺循环”的限制，能量转换效率高达70%～80%，实际使用效率则是普通内燃机的2～3倍.但燃料电池要获得更高的功率密度和性能，须在相对高的气体压力下工作，尤其是对于阴极的反应物(氧气或者空气)而言.因此，需要设计一个空气压缩机，为大功率燃料电池发动机提供高压空气，实现进气增压的目的. 由于燃料电池特殊场景使用要求，空压机有很多有待解决的技术难点.一方面，为保证燃料电池的核心部件质子交换膜具有良好的电化学工作特性，要求提供给燃料电池堆的压缩空气绝对干净；另一方面，为保证燃料电池具有良好的综合性能，要求该系统能够根据燃料电池输出功率的大小调整供气流量与压力，当前燃料电池空压机须满足无油、小型、高压、超高转速和功耗少的要求.

目前国内外燃料电池发动机主要采用离心式高速空压机，为提高燃料电池发动机的体积比功率，采用超高速电机直驱方式，避免使用传统增速机构的冗余设计方式.其工作原理是超高速电机转子-主轴-叶轮一体化设计，自然空气在离心力作用下，气体被挤压到叶轮后方扩压器中.而在叶轮中间形成稀薄地带，前面的气体从叶轮中间的进气部分进入叶轮，由于叶轮连续高速旋转导致气体能不断地被挤压出去，从而保持空压机中气体的连续流动.气体因离心作用增加了压力，以很大的速度离开工作叶轮，气体经扩压器会逐渐降低了速度，动能转变为静压能，进一步增加了压力，实现进气增压目的.

空压机转子的转速在50 000～100 000 r/min之间，两端采用轴承支撑的悬臂梁结构，转子安全高速运行是空压机连续工作的前提，作为空压机核心部件的转子-轴承动力学分析得到越来越多的关注[1].转子和轴承决定着整台空压机的寿命.由于燃料电池进气压缩高压比要求，空压机转子的转速不断提高，转子与轴承间的作用不断增大，从而使得转子振动过载和振幅增大，到某一转速时振幅达到最大值(共振)，转子寿命减低，这一转子振幅最大的转速称为转子的临界转速(转子固有频率).转子由于自重的原因，在悬臂梁支撑形式的轴承之间产生一定挠度.此外，转子虽然经严格的动平衡修正，但仍不可避免地存在着微小的偏心，导致转子重心与转子旋转轴线不完全吻合，在旋转时产生一种周期性变化的离心力，使转子产生横向振动，这种振动在临界转速上表现十分明显.为确保空压机在工作转速范围内不发生共振，临界转速要适当远离空压机工作转速区，避免转子在受到某种激励之后产生的共振给空压机转子带来严重损坏.

转子系统的动力可靠性对于确保燃料电池超高速空压机的转子系统能够长时间安全可靠运行具有十分重要的理论研究和实际工程应用价值.在转子动力学分析方面国内外都做了不少关于转子临界转速的研究工作.国内学者钟一谔[2]、闻邦椿[3]、虞烈[4]等在转子-轴承系统设计、临界转速分析、响应仿真计算等方面做了大量基础的研究工作，对高速旋转机械设计提供了丰富的理论基础，这些研究主要集中于压缩机、水轮机、汽轮发电机等大功率转子系统研究.周强[5]和王天煜[6]分别研究了陶瓷滚动轴承和磁力轴承支撑结构对电机转子临界转速和轴心轨迹等的影响.其中王天煜[7]等进一步分析了转子结构对电机临界转速的影响，并采用样机振动实验验证其计算方法的正确性.李啸天[8]等基于ANSYS有限元软件对空压机转子结构进行了模态分析，得到了转子系统的固有频率和振型，避免工作转速达到临界转速产生共振现象.陈龙等[9]不仅利用有限元软件校核空压机中圆轴的强度、刚度和针对临界转速进行分析，还在满足强度要求下对轴进行优化设计.戴继双等[10]对大型离心压缩机转子系统结构参数优化设计，以转子系统弯曲振动的前二阶临界转速为目标函数，转轴的部分长度和直径作为设计变量来建立转子系统的有限元优化模型.此外，国内外对大型工业用压缩机分析也做了许多研究[11-12]，目前针对中小型功率等级超高速燃料电池空压机的研究较之偏少，但前人的研究在基础理论和研究方法方面具有很好的借鉴意义.本文在分析转子-轴承系统悬臂梁支撑特性的基础上，采用有限元法对燃料电池空压机超高速电机转子-轴承系统进行动力学建模仿真研究，考虑转子在燃料电池空压机典型工作区间内的不同转速下的临界转速.我们针对某燃料电池汽车用空压机永磁电机转子-轴承进行动力学仿真分析，研究轴承刚度、轴承间跨距以及转轴质量对空压机转子-轴承临界转速的影响，以便提出提高临界转速的建议.

1 转子-轴承有限元模型

转子-轴承系统振动特性分析方法主要有解析法、传递矩阵法、有限元法、不平衡响应法及模态合成法.解析法和模态合成法主要针对的是简单转子求解理论解，而有限元法及传递矩阵法主要应用于复杂的多盘或多轴承系统.有限元法与传递矩阵法相比，能够更充分地模拟转子的振动特性，且具有较好的计算精度[13].

转子作为高速空压机旋转机械的核心部件，本身零件数量多，属于大型装配体，在高温、高压、高流量的环境中运行，所涉及的相关理论复杂，如流体力学、工程热力学、机械学、固体力学、材料力学等.这里主要考虑燃料电池空压机转子动力学特性的主要影响因素，对转子系统进行简化，有利于降低问题的复杂程度，且节省计算时间.根据高速空压机的转子轴承系统结构，由于转子各零件材料密度相近，整个转子可等效为一段梁.同时将叶轮以等效质量点方式，通过实常数定义转动惯量和质量，这样和建立三维实体的叶轮模型对临界转速的影响相近.此外，一维模型和三维模型中均使用同一单元模拟轴承，考虑到一维模型实际建模便利性和运算上快速优势，综合考虑采用一维模型模拟仿真整个空压机转子-轴承系统.图1为转子轴承系统的一维模型示意图.

空压机转子-轴承依据其结构直径的不同设置不同的截面直径，并根据转轴材料设置相应的密度、杨氏弹性模量以及泊松比，还需注意定义各自的材料阻尼.表1为空压机转轴和转子的材料属性.

表1 转轴和转子的材料属性

轴端叶轮等效为质量点，通过设置将叶轮的质量、极转动惯量和直径转动惯量等属性添加到质量点上，使其模拟叶轮对转子-轴承系统固有特性的影响.叶轮的质量为0.149 kg，极转动惯量JP=7.405×10-5kg·m2，直径转动惯量JD=4.37×10-5kg·m2.轴承将其等效为弹簧阻尼系统，并通过实常数的设置来确定弹簧的刚度值和阻尼的大小，忽略轴承阻尼，轴承刚度皆为2.69×107N/m.图2为在网格划分后显示单元属性的转子轴承模型.

图1 转子-轴承系统的一维模型Figure 1 1D model of rotor-bearing system

由于本转子轴承系统不考虑剪切和扭矩影响，因此边界条件设置只需对模型节点的平动和转动位移进行约束，其中轴承固定.因为分析整个转子轴承系统的临界转速，需要考虑陀螺效应所造成的影响.由于陀螺效应，旋转机械结构的特征频率与其旋转速度相关，计算不同旋转速度时的频率，可以得到各个模态频率随转动速度的变化曲线(坎贝尔图).

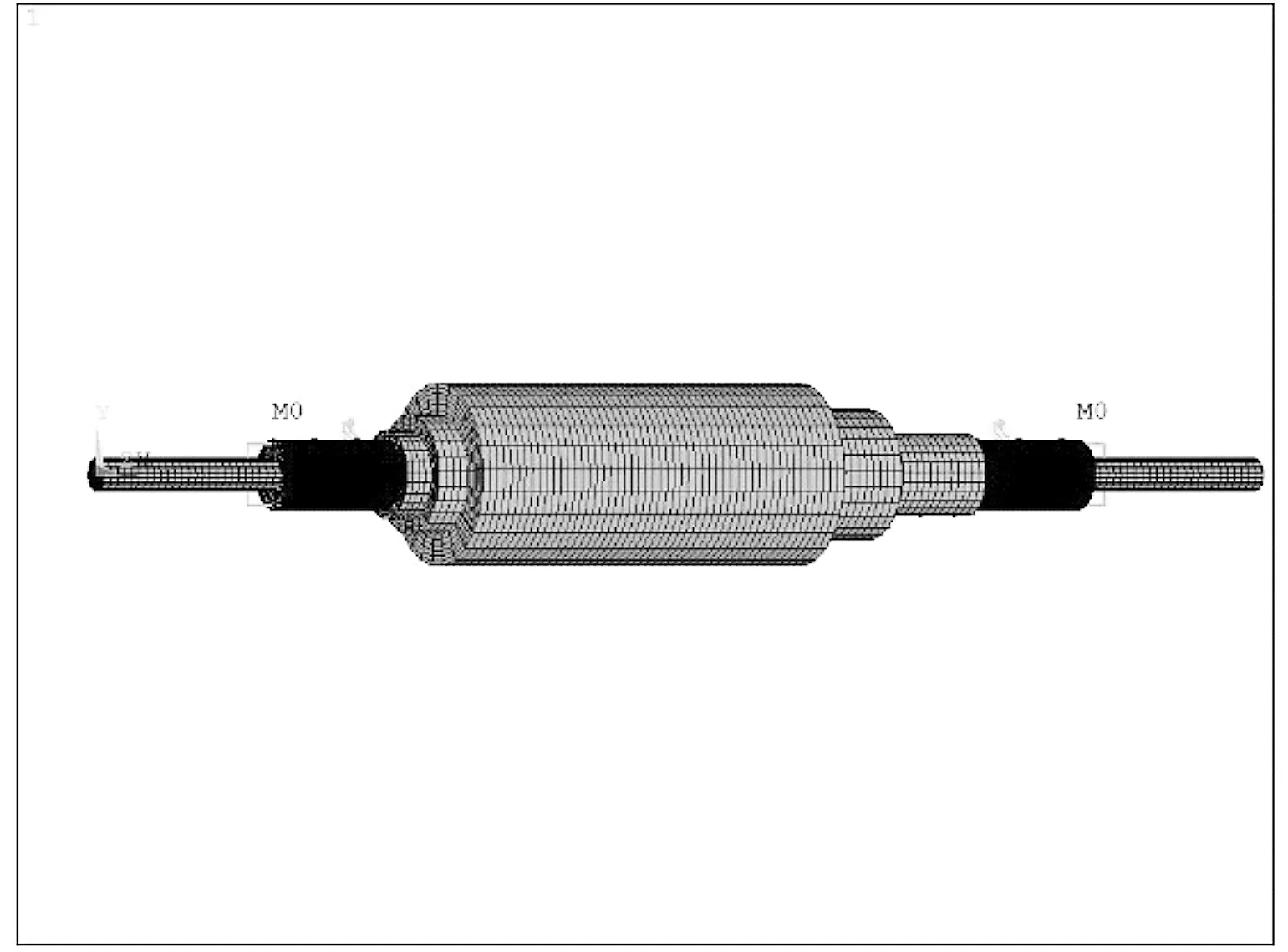
图2 网格划分后显示单元属性的转子-轴承模型Figure 2 Rotor-bearing model after meshing

2 模型仿真结果分析

根据所设置的参数对空压机转子-轴承系统进行数值仿真计算，图3为坎贝尔图和交点转速数值.

从图3中可以看出，转子轴承系统在0～80 000 r/min转速范围内激励直线与频率曲线一共有4个交点，由图4可知这四个交点所对应的转子转速分别为46 177 r/min(CRIC1)，46 290 r/min(CRIC2)，63374 r/min(CRIC3)和69 228 r/min(CRIC4).在计算转子轴承系统的临界转速时，通常只考虑同步正向涡动时的振动频率，这是因为在实际转子运行时，由于不平衡激励力的存在，转子将做同步正向涡动，通常说的临界转速，一般是指同步正向涡动的临界转速.由坎贝尔图可以看出，第一个与第三个交点所对应的频率为反进动的频率，而第二个与第四个交点所对应的频率为正进动的频率.因此转子轴承系统在所给转速范围内存在两阶临界转速，其数值分别为46 290 r/min和69 228 r/min.

对于本转子轴承系统，现在得到的一阶临界转速相对较低，容易与燃料电池空压机正常工作区间发生共振，不能满足转子-轴承系统在额定转速下安全稳定地运行，因此对现有的轴承参数进行改善调整，以满足提高转子-轴承系统一阶临界转速高于空压机工作区间转速要求，目标是让其一阶临界转速高于50 000 r/min.

3 转子-轴承系统临界转速提高的改善措施

3.1 轴承刚度

最简单的改进方案就是对轴承参数进行修改，以实现不修改整体结构的情况下改善转子-轴承系统的临界转速.为了提高转子轴承系统的临界转速，可以考虑选用内径相同但刚度值不同的轴承.通过对参数化模型模拟仿真，当轴承刚度为3.69×107N/m的轴承时，重新计算结果如图5～6.

图5 调整轴承刚度后的坎贝尔图Figure 5 Campbell chart after modifying stiffness

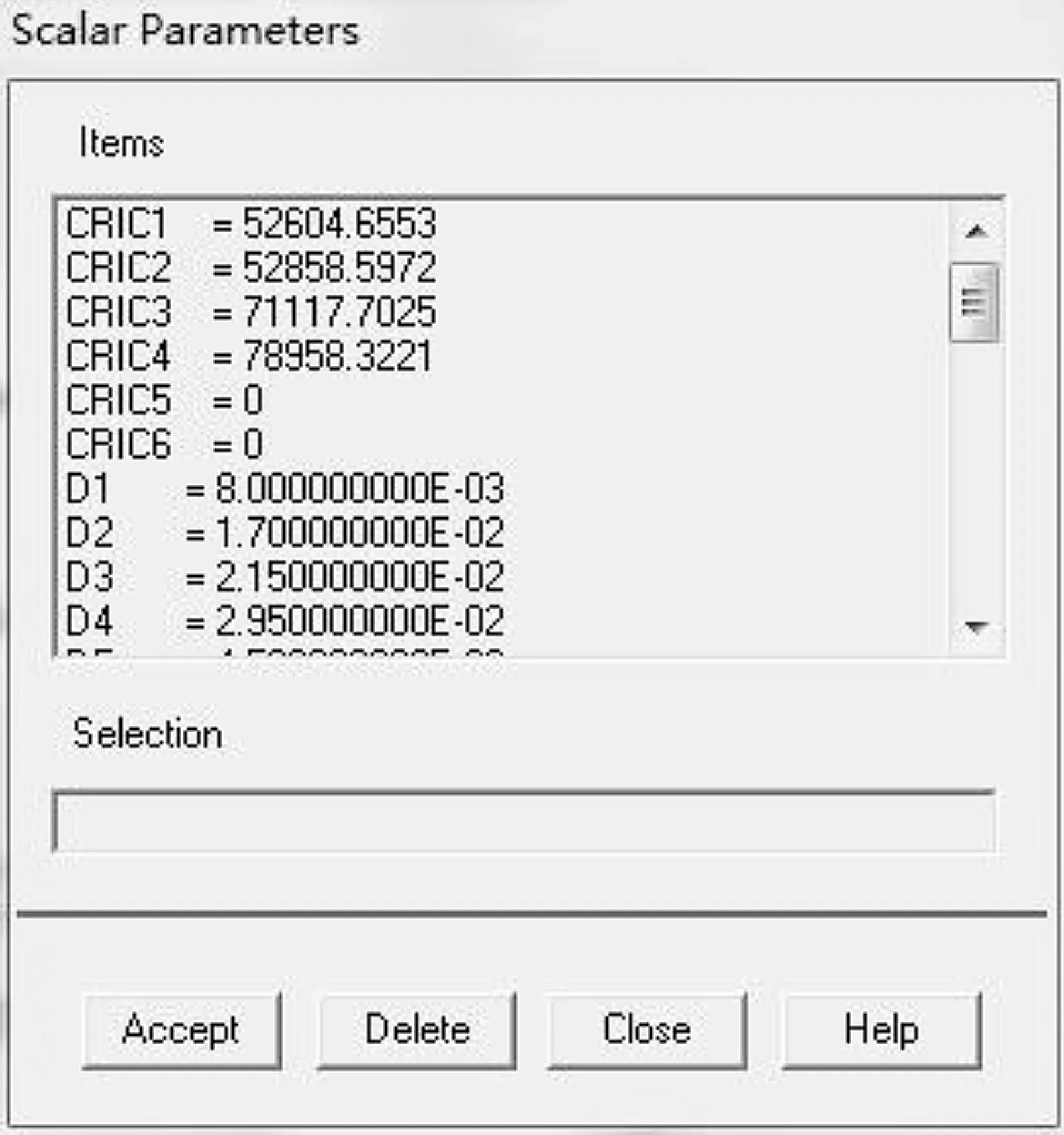
图6 1～4阶临界转速数值Figure 6 1st to 4th critical speed value

从图5和6中可以看出，转子-轴承系统一阶临界转速从46 290 r/min提高到52 858 r/min，二阶临界转速也相应提高.由此可以看出，随着轴承刚度的增加，转子-轴承系统的临界转速也随之增加.提高轴承刚度的方法在工程上通过增加轴承预紧力的方式实现，但增加预紧力同时会降低高速轴承工作寿命，所以不能完全通过提高刚度的方法增加转子-轴承系统的一阶临界转速.

3.2 轴承跨距

除了改变轴承刚度来改善系统临界转速外，轴承跨距也可以对系统临界转速产生影响.现假设在不改变转子-轴承系统整体长度的情况下，将轴承向内各移动10 mm，实现两个轴承间的跨距减小20 mm.图4.3为减小轴承间跨距后运行程序所得的坎贝尔图，图4.4为通过输入命令获得的交点转速数值.

从图7～8中可以看出，转子轴承系统的一阶临界转速从46 290 r/min提高到47 608 r/min，二阶临界转速则有所降低.由此可知，在轴承间跨距减小的情况下，转子-轴承系统的临界转速能够提高，同时也拉近了一阶转速与二阶转速间的差距.因此在实际优化过程中可以适当减小轴承间跨距作为辅助提高临界转速的方法.

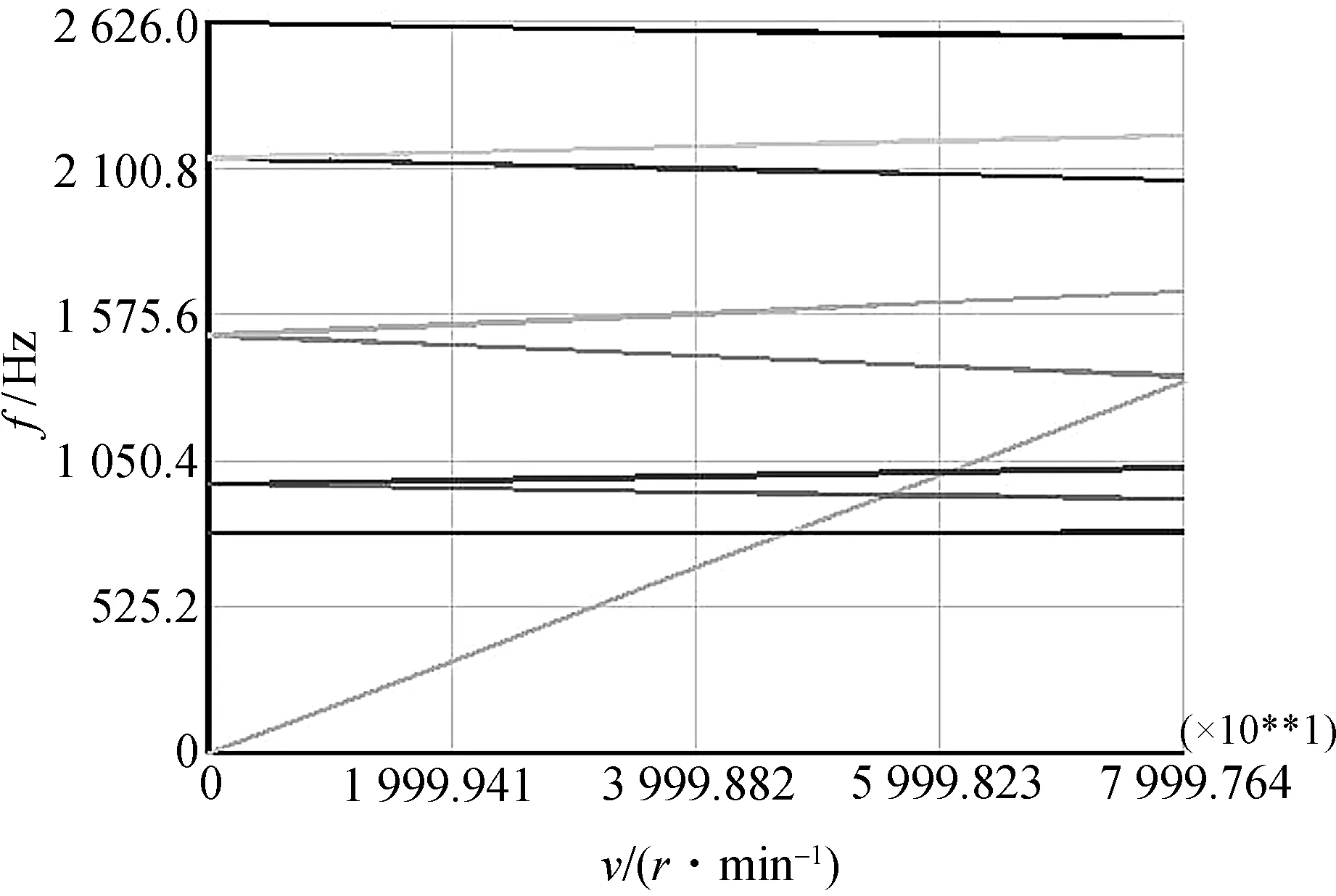
图7 减小轴承间跨距后坎贝尔图Figure 7 Campbell chart after reducing bearing span

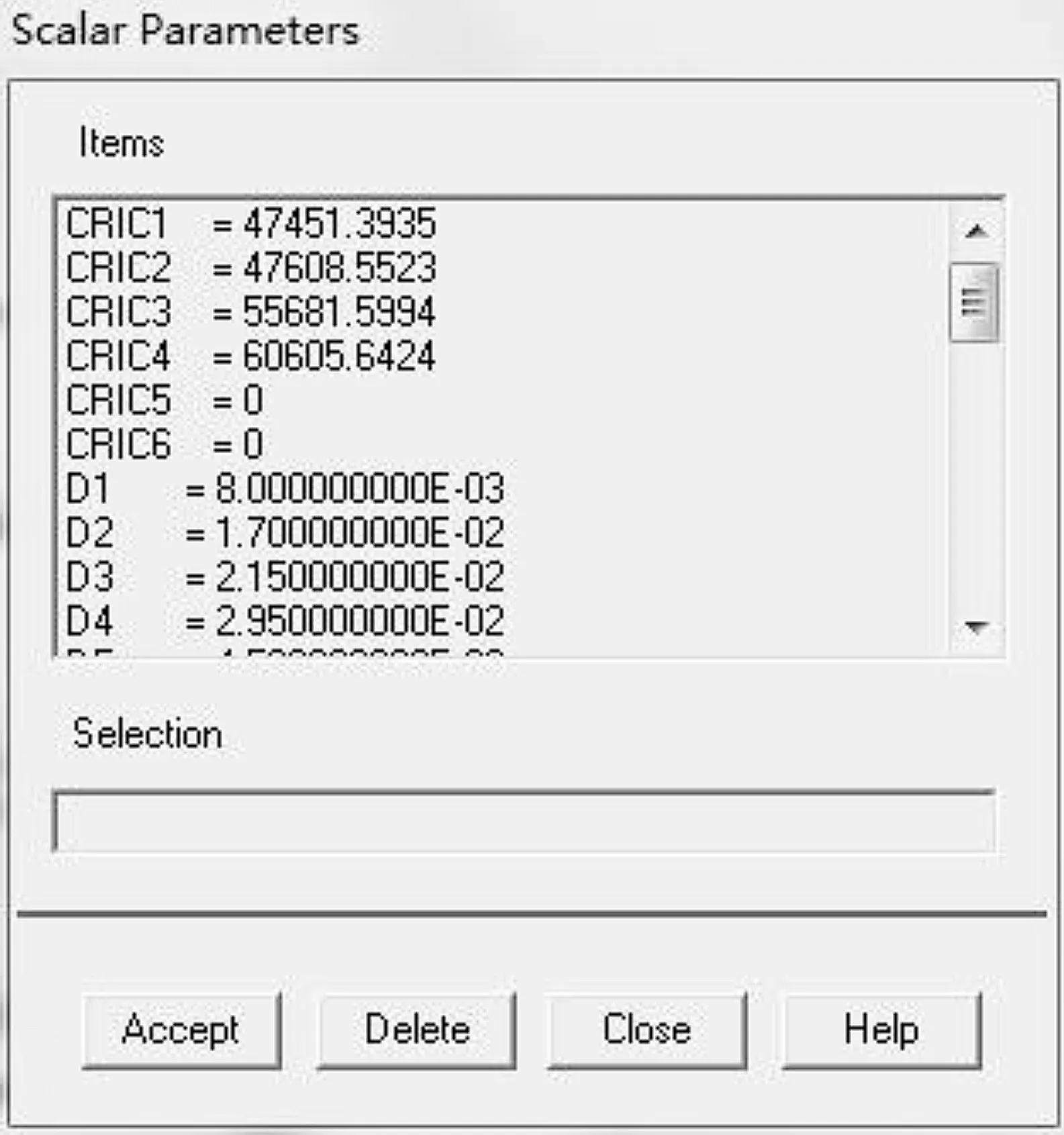
图8 1～4阶临界转速数值Figure 8 1st to 4th critical speed value

3.3 转轴质量

除了对轴承进行优化以外，还可以对转轴进行质量改进以达到提高临界转速的目的.要改变转轴的质量，在不改变转轴结构的前提下可以调整转轴的材料.在保证机械性质基本不变的情况下，选用密度不同的材料就可以改变转轴的质量.现使用的转轴密度为7 800 kg·m-3，如转轴密度为6 000 kg·m-3的材料用作转轴，使转轴的质量降低.图9为降低转轴质量后运行程序所得的坎贝尔图，图10为通过输入命令获得的交点转速数值.

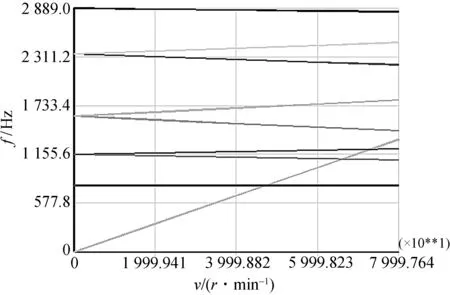
图9 降低转轴质量后坎贝尔图Figure 9 Campbell chart after reducing mass of shaft

图10 激励直线与频率曲线交点转速数值Figure 10 1st to 4th critical speed value

从图9～10中可以看到，转子-轴承系统的一阶临界转速从46 290 r/min提高到47 284 r/min，二阶临界转速也相应提高.由此可以看出，在转轴的质量下降之后，转子轴承系统的临界转速整体提高，说明轻质转轴有利于提高空压机临界转速.

为了减轻转轴的质量，除了选用轻质材料替代以外，还可以将转轴由实心轴结构变为空心轴结构.在不改变其机械性质的情况下，在转轴中心开孔，不仅有助于减轻转轴的整体质量，还有助于提高整个转子轴承系统的散热.

3.4 其他改善措施

除了以上因素外，还可以通过改变结构，缩短叶轮处转轴长度，降低可能存在的阻尼等方法来提高转子轴承系统的临界转速，但都需结合实际情况进行分析.要完成整个转子轴承系统的临界转速优化，就必须综合考虑所有的影响因素，从中选择最优的方案.

4 结 语

通过对燃料电池车用高速空压机所使用的高速永磁电机转子-轴承系统进行转子动力学临界转速分析，可得出主要结论以下：

1)针对燃料电池空压机转子的断轴破坏问题，可以采用有限元建模方法，进行转子动力学分析，可以采用提高坎贝尔图激励直线与各阶频率曲线的交点对应的临界转速的方法来避免共振发生.

2)提高轴承刚度、缩短轴承跨距和降低转轴质量等重要影响因素可提高转子-轴承系统的临界转速，避免共振发生.此外，其他一些结构因素也会影响临界转速的大小，在实际工程应用中需要综合考虑，选取最合适的设计方案.

[1] LEE Y B, PARK D J, KIM C H, et al. Rotordynamic characteristics of a micro turbo generator supported by air foil bearings[J]. Journal of Micromechanics & Microengineering,2007,17(2):297-303.

[2] 钟一鄂,何衍宗,王正.转子动力学[M].北京:清华大学出版社,1987:65-67.

[3] 闻邦椿,顾家柳,夏松波.高等转子动力学[M].北京:机械工业出版社,2000:45-65.

[4] 虞烈,刘恒.轴承—转子动力学[M].西安:西安交通大学出版社,2001:25-28.

[5] 周强,刘闯,朱学忠,等.超高速开关磁阻电动机设计[J].中国电机工程学报,2009,29(9):87-92. ZHOU Q, LIU C, ZHU X Z, et al. Design of super high speed switched reluctance motor[J]. Proceedings of the CSEE,2009,29(9):87-92.

[6] 王天煜,王凤翔,方程.高速永磁电机机组轴系振动研究[J].振动与冲击,2011,30(9):111-115. WANG T Y, WANG F X, FANG C. Vibration analysis of shafting of high speed permanent magnetic machinery[J]. Journal of Vibration and Shock,2011,30(9):111-115.

[7] 王天煜，王凤翔，方程.高速电机转子临界转速计算与振动模态分析[J].辽宁工程技术大学学报(自然科学版),2009,28(5):804-808. WANG T Y, WANG F X, FANG C. Critical speed calculation and mode analysis of rotor for high speed rotor[J]. Journal of Liaoning Technical University (Natural Science),2009,28(5):804-808.

[8] 李啸天，韩振南.基于ANSYS软件的转子系统临界转速及模态分析[J].机械管理开发，2010,25(3):184-185. LI X T, HAN Z N. Rotator critical rotational speed and modali analysis based on ANSYS[J]. Mechanical Management and Development,2010,25(3):184-185.

[9] 陈龙，文湘隆，丁国平.基于有限元分析的轴的设计[J].现代机械，2005(1):36-38. CHEN L, WEN X L, DING G P. Design of axle based on finite element analysis (FEA)[J]. Modern Machinery,2005(1):36-37.

[10] 戴继双，马辉，孟磊，等.大型离心压缩机转子系统结构参数优化设计[J].机械与电子，2009(8):24-26. DAI J S, MA H, MENG L, et al. Optimization design of structural parameters of rotor system in a large centrifugal compressor[J]. Machinery & Electronics,2009(8):24-26.

[11] 瓮雷，杨自春，曹跃云.转子系统临界转速计算及不平衡响应分析[J].四川兵工学报,2012，33(11):65-69. WENG L, YANG Z C, CAO Y Y. Calculation of critical speed and analysis of unbalance response of rotor system[J]. Journal of Sichuan Ordnance,2012,33(11):65-69.

[12] 张利民，王克明，吴志广.利用ANSYS进行转子临界转速计算[J].沈阳航空工业学院学报,2010,27(5):34-37. ZHANG L M, WANG K M, WU Z G. Rotor critical speed analysis on ANSYS[J]. Journal of Shenyang Aerospace University,2010,27(5):34-37.

[13] 黄龙.高速离心式压缩机转子动力学有限元分析[D].武汉:华中科技大学，2012. HUANG L. Finite Element Analysis for High-speed Centrigugal Compressor Rotor Dynamics[D]. Wuhan: Huazhong University of Science and Technology,2012.

Analysis and improvement of rotor dynamics for super high-speed air compressors applied in fuel cell vehicles

ZHAN Jian1,2, ZHANG Zhiming1,2, ZHANG Juannan3, LI Changhao1,2, NI Yue1,2

(1.School of Automotive Studies, Tongji University, Shanghai 201804, China; 2.Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China; 3. College of Physical Science and Engineering, Tongji University, Shanghai 200092, China)

Higher pressure gas fuel produced by the air compressor can augment the power density and performance of fuel cell engines, but the rotor-bearing system of air compressors may have practical problems of resonance and loss of stability, or even broken shaft damages. The critical speed of the rotor-bearing system was analyzed and the main relevant factors on the air compressor’s critical speed were studied such as bearing stiffness, bearing position, and the mass of the rotation shaft. Numerical simulation results show that both increasing bearing stiffness and decreasing bearing span and its mass can augment the critical speed of air compressors.

fuel cell air compressor; super speed rotor-bearing system; rotor dynamics; critical speed

2096-2835(2017)02-0169-07

10.3969/j.issn.2096-2835.2017.02.006

2017-03-06 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

国家自然科学基金资助项目(No.51405344)，国家科技支撑计划资助项目(No.2015BAG06B01)，中央高校博士点基金资助项目(No.20130072120041)，47期留学回国人员科研启动基金，中央高校业务费(No.1600219247)，公路养护装备国家工程实验室开放基金资助项目(No.310825151129).

詹剑(1983-)，男，福建省建阳人，硕士研究生，主要研究方向为燃料电池发动机及关键零部件技术. E-mail:83zhanjian@tongji.edu.cn 通信联系人：张智明，男，讲师.E-mail: zhangzm@tongji.edu.cn

TH138

A