一种热电偶时间常数测试系统

2017-07-05孙宏健李文军李佳琪郑永军

中国计量大学学报 2017年2期

关键词：铜镍时间常数热电偶

孙宏健,李文军,李佳琪,郑永军

(中国计量大学计量测试工程学院,浙江杭州 310018)

一种热电偶时间常数测试系统

孙宏健,李文军,李佳琪,郑永军

(中国计量大学计量测试工程学院,浙江杭州 310018)

时间常数是检测热电偶动态测试性能的重要指标.为了衡量热电偶的动态测试性能,设计了一种热电偶时间常数测试系统,包括热电偶、恒温槽、数据采集卡、激光对射式光电传感器.测试过程中,由激光对射式光电传感器记录热电偶接触恒温槽恒温介质时间点,由数据采集卡采集热电偶的温度数据以及激光对射式光电传感器的电压数据,由数据采集软件显示并记录温度与电压变化曲线.对热电偶的温度数据进行了拟合,测得热电偶的时间常数并与理论计算值进行了比较.最后对测试过程产生的误差进行了分析.分析结果表明，该热电偶时间常数测试系统可大幅度减少热电偶自身的热惰性所引起的测量误差，但仍会产生其它微小测量误差.

热电偶;数据采集;激光对射式;光电传感器;时间常数

在工业领域中,温度是十分重要的衡量指标.由于热电偶具有装配简单、性能稳定、测温范围广和响应时间快等优点[1],所以在多个领域中热电偶成为了应用广泛的测温传感器.时间常数是检测热电偶动态测试性能的重要指标[2],检测热电偶的时间常数对于热电偶具有重要意义.影响热电偶时间常数的因素有很多,时间常数大小与热电偶的物性参数、几何参数以及测温环境等物理因素有关[3],其中测温环境对其影响较显著，因此很难用简单的理论模型准确求得热电偶时间常数,在实际检测中热电偶时间常数通常用实验的方法得到.因此,研究能准确快速测量热电偶时间常数的方法具有重要价值[4].

本文设计了一种热电偶时间常数测试系统,其机械装置组装方便,结构简单,操作省时省力.

1 测试系统设计

温度传感器的输入量随时间变化的响应特性称为动态响应特性,反映了测量温度随实测温度的变化而变化的程度[5],传统的分析模型都是可以假设忽略传感器内部温度分布、传感器导热和辐射的热交换[6],一般可以用微分方程或传递函数的形式表示.

对温度传感器做动态响应测试,认为其系统为一阶线性,其响应状态用微分方程表示为

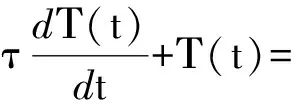
(1)

式(1)中:τ—时间常数，通常由实验获得;T—温度随时间而变化的函数;Τ(t)—实验记录的结果.

如τ过大,显然Τ(t)≠Τ,存在动态误差.

对于热电偶来说,其阶跃响应为

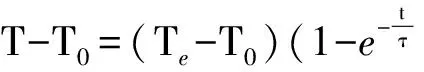
(2)

式(2)中:T—热电偶实测温度;Τ0—热电偶初始温度;Τe—阶跃温度;t—阶跃温度产生所需时间;τ—热电偶时间常数.

当t=τ,式(2)变为

T-T0=(Te-T0)(1-e-1)=0.632(Te-T0).

(3)

根据式(3),时间常数是指热电偶实测温度T与初始温度Τ0之差达到温度阶跃(Τe-Τ0)的63.2%处所需的时间[7].热电偶动态响应曲线如图1.

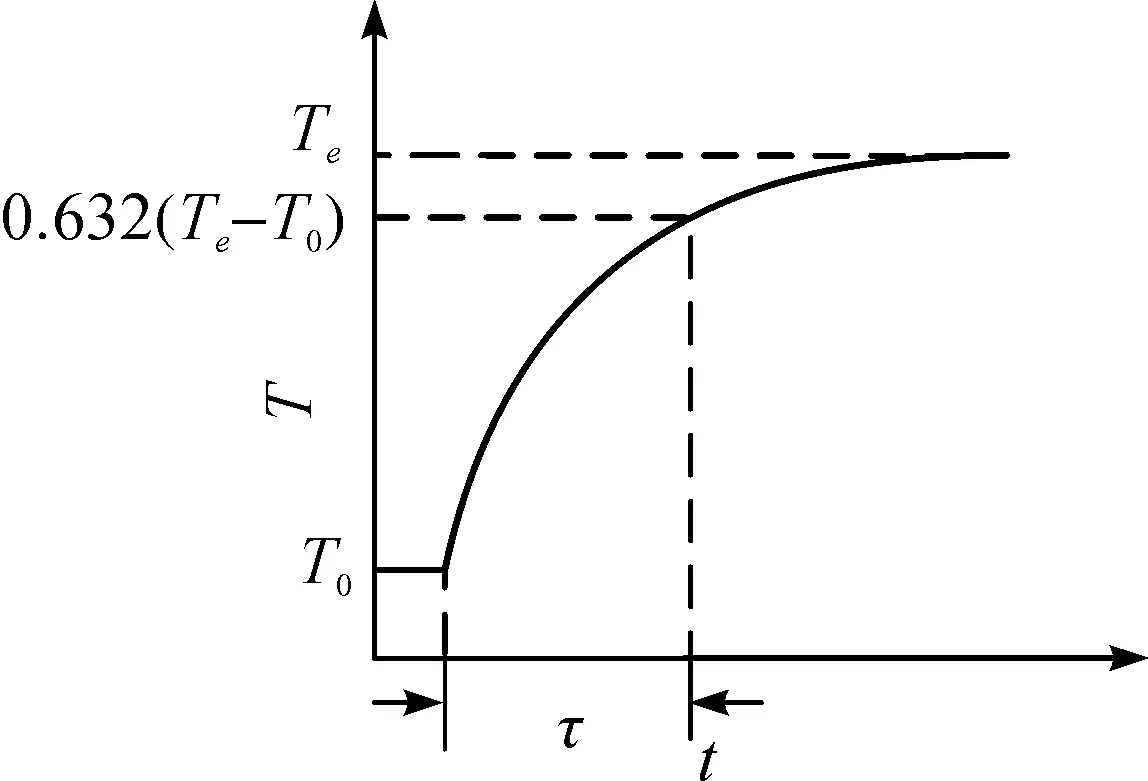
图1 热电偶动态响应曲线Figure 1 Response curve of thermocouple

1.1 测试系统硬件设计

热电偶时间常数测试系统硬件包括恒温槽、热电偶、激光对射式光电传感器、数据采集卡和计算机.恒温槽选用RTS-40A制冷恒温槽,恒温介质为水,温度范围为-40～95 ℃;热电偶选用偶丝直径0.1 mm的铜-铜镍K型热电偶与偶丝直径0.4 mm的铜-铜镍K型热电偶各一支;激光对射式光电传感器选用M12 NPN常开型防水激光对射式光电传感器(以下称为M12激光对射式光电传感器),数据采集卡选用USB-2408数据采集卡,测试系统的结构示意图如图2.

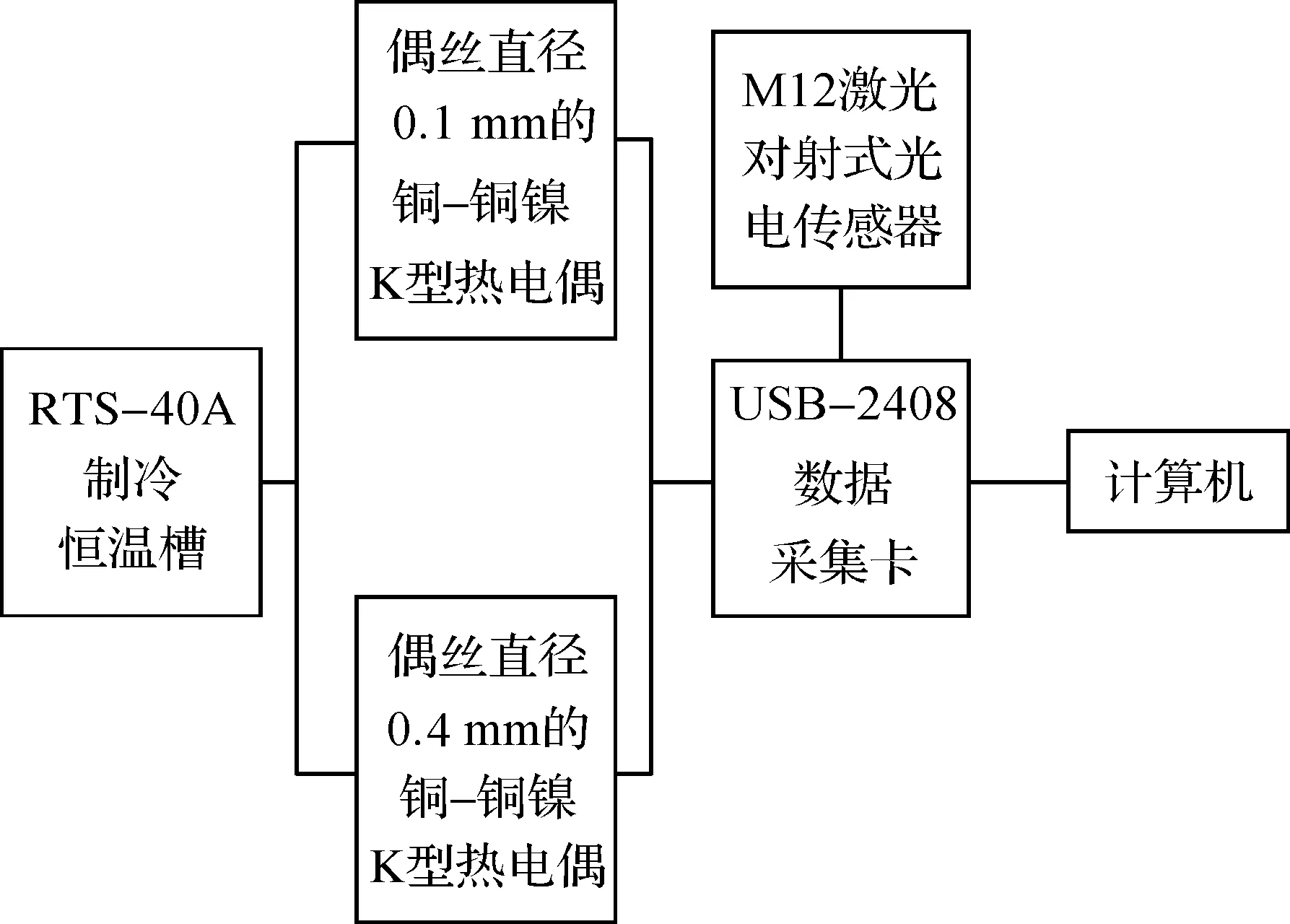
图2 测试系统结构示意图Figure 2 Schematic structure of the test system

图2中,由M12激光对射式光电传感器记录两支铜-铜镍K型热电偶接触RTS-40A制冷恒温槽恒温介质时间点,可以减少两支铜-铜镍K型热电偶测量滞后引起的测量误差,提高测量精度;USB-2408数据采集卡能记录两支铜-铜镍K型热电偶的温度信息以及M12激光对射式光电传感器电压信息.

1.2 测试系统机械设计

热电偶时间常数测试系统机械装置如图3.

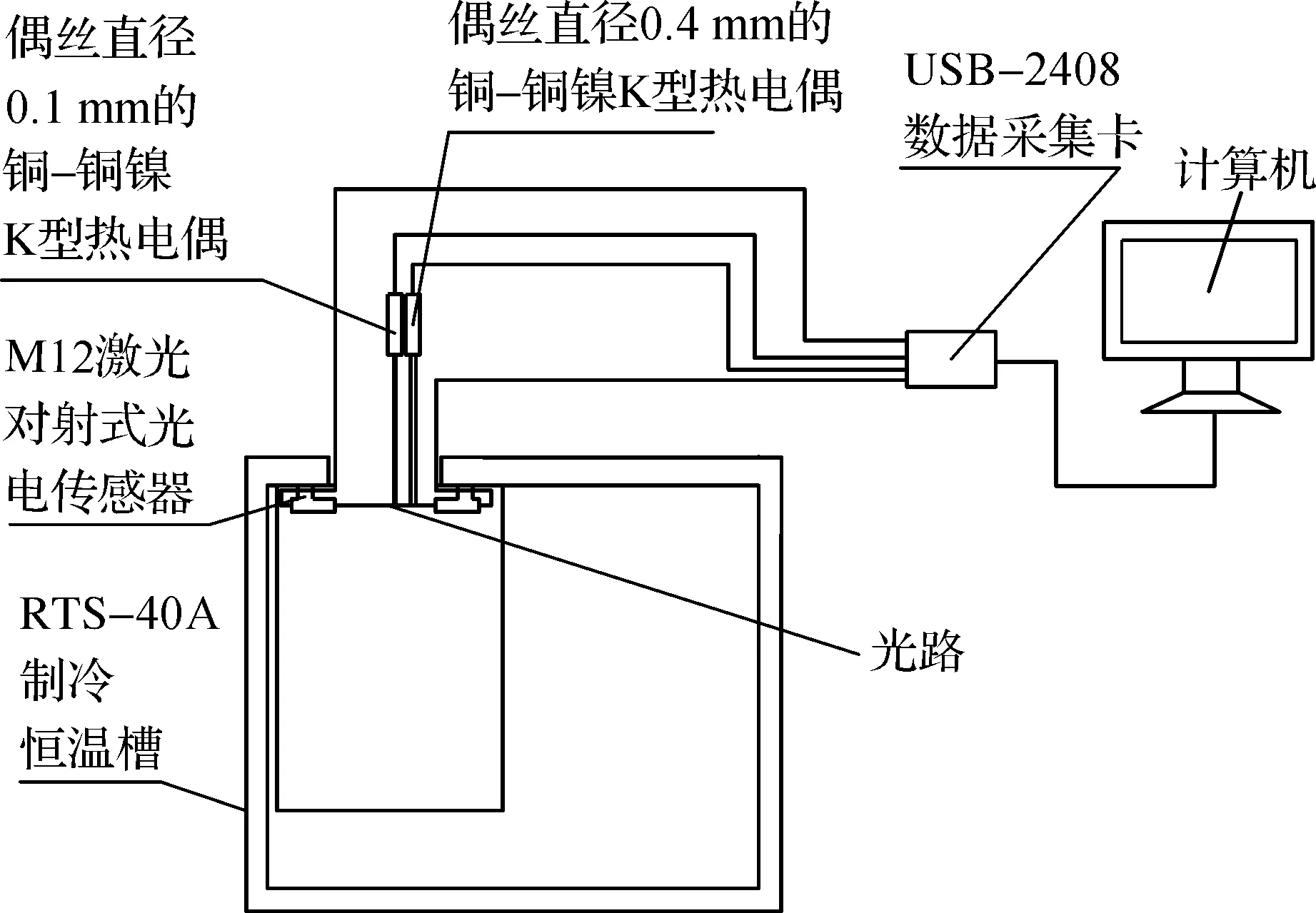
图3 测试系统机械示意图Figure 3 Mechanical sketch map of the test system

图3中,RTS-40A制冷恒温槽的恒温介质为水,M12激光对射式光电传感器会产生可见光路[8].M12激光对射式光电传感器的底座对称焊接在RTS-40A制冷恒温槽顶部内壁,使光路可以经过RTS-40A制冷恒温槽的插入孔径正下方,RTS-40A制冷恒温槽的恒温介质水平面高度与M12激光对射式光电传感器产生的光路平齐.

1.3 测试系统软件设计

选用TracerDAQ数据采集软件,测试系统软件原理框图，如图4.

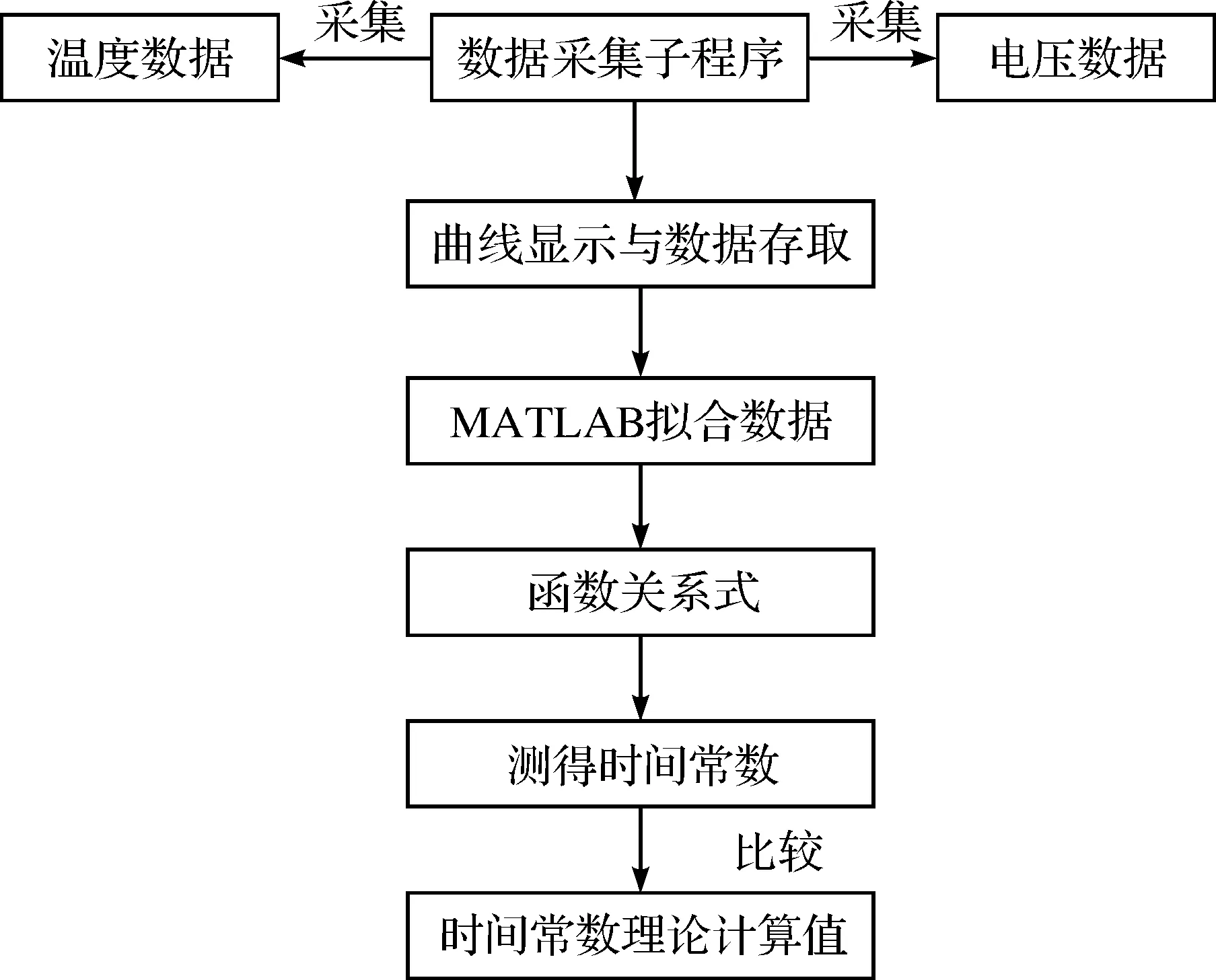
图4 测试系统软件原理框图Figure 4 Software principle diagram of the test system

在软件部分,主要负责对USB-2408数据采集卡采集的数据进行分析处理、实时显示、存储.USB-2408数据采集卡的数据采集子程序能同时采集两支铜-铜镍K型热电偶的温度数据与其对应的时刻,以及M12激光对射式光电传感器的电压数据及其对应的时刻,并通过TracerDAQ数据采集软件生成相应的曲线,根据采集的数据测得时间常数.最后通过MATLAB对温度数据进行拟合,得到拟合曲线及其函数关系式.

2 实验

2.1 实验步骤

具体实验步骤如下:

1)将两支铜-铜镍K型热电偶置于室温环境中,并与USB-2408数据采集卡相连,在室温中静置30 min以待两支铜-铜镍K型热电偶温度稳定.

2)将RTS-40A制冷恒温槽恒温介质温度分别设定为80 ℃、84 ℃、88 ℃,并等待其示数平稳.

3)将M12激光对射式光电传感器输入端连接信号发生器,输出端连接USB-2408数据采集卡,信号发生器为M12激光对射式光电传感器提供10 V直流电压,若没有物体遮挡光路,M12激光对射式光电传感器的输出电压为0 V,当两支铜-铜镍K型热电偶的保护套管阻挡光路,则M12激光对射式光电传感器输出端的电压会突变为10 V[9].实验中,将M12激光对射式光电传感器电压阶跃的瞬间作为两支铜-铜镍K型热电偶响应的计时起点.

4)将USB-2408数据采集卡与计算机相连,设置TracerDAQ数据采集软件的参数,其中采样频率为200 Hz.

5)将两支铜-铜镍K型热电偶的测量端对齐,然后快速垂直插入温度恒定的RTS-40A制冷恒温槽恒温介质中,并使两支铜-铜镍K型热电偶至少一支能经过并阻挡光路,同时USB-2408数据采集卡开始采集数据,TracerDAQ数据采集软件实时显示响应曲线[5].

6)测试结束后,将两支铜-铜镍K型热电偶从RTS-40A制冷恒温槽恒温介质中取出,使其静置到初始状态.将存储的动态响应曲线及数据记录下来,最后用MATLAB对温度数据进行拟合.

2.2 实验结果

按以上实验步骤进行测试,分别对两支铜-铜镍K型热电偶置于不同水温进行3次实验,当天室温为25 ℃左右.根据测得的数据得到两支铜-铜镍K型热电偶的时间常数,实验结果如表1,其中偶丝直径0.1 mm的铜-铜镍K型热电偶用Φ0.1表示,偶丝直径0.4 mm的铜-铜镍K型热电偶用Φ0.4表示.

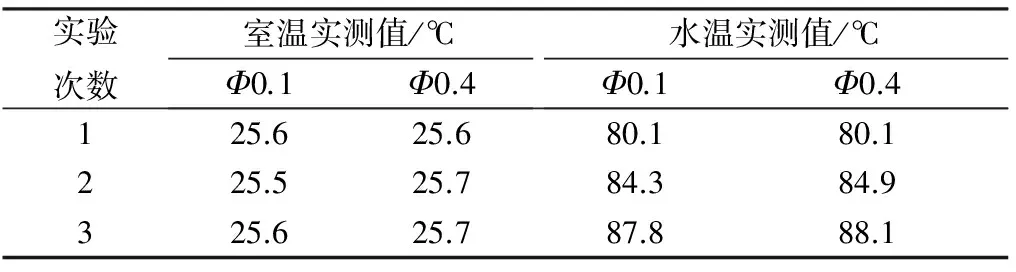
表1 热电偶动态响应数据

其中,第三次实验测试曲线如图5.

图5 热电偶动态响应曲线Figure 5 Curves of thermocouples dynamic response

图5中,CH0通道为偶丝直径0.1 mm的铜-铜镍K型热电偶实时温度变化曲线,CH1通道为M12激光对射式光电传感器实时电压变化曲线,CH2通道为偶丝直径0.4 mm的铜-铜镍K型热电偶实时温度变化曲线.

可以看出,两支铜-铜镍K型热电偶的响应速度比M12激光对射式光电传感器略慢,事实上当M12激光对射式光电传感器电压突变的时刻两支铜-铜镍K型热电偶开始与RTS-40A制冷恒温槽恒温介质进行对流换热,所以记录下M12激光对射式光电传感器的响应起始时刻作为两支铜-铜镍K型热电偶的响应计时起点.其中M12激光对射式光电传感器的响应时间为5 ms.

2.3 数据拟合

将第三次实验中温度数据运用MATLAB拟合工具箱进行拟合,选用Aexp(b×x)+Cexp(d×x)指数函数形式进行指数逼近.通过对偶丝直径0.1mm的铜-铜镍K型热电偶与偶丝直径0.4 mm的铜-铜镍K型热电偶的温度数据分别进行拟合,检验热电偶时间常数测试系统是否可靠.拟合结果,如图6与图7.

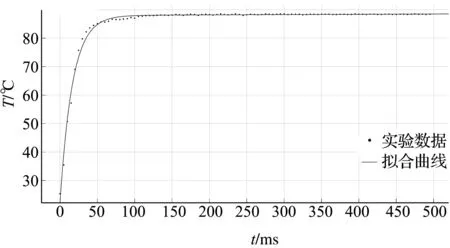
图6 热电偶(Φ0.1)动态响应拟合曲线Figure 6 Dynamic response fitting curve of thermocouple(Φ0.1)

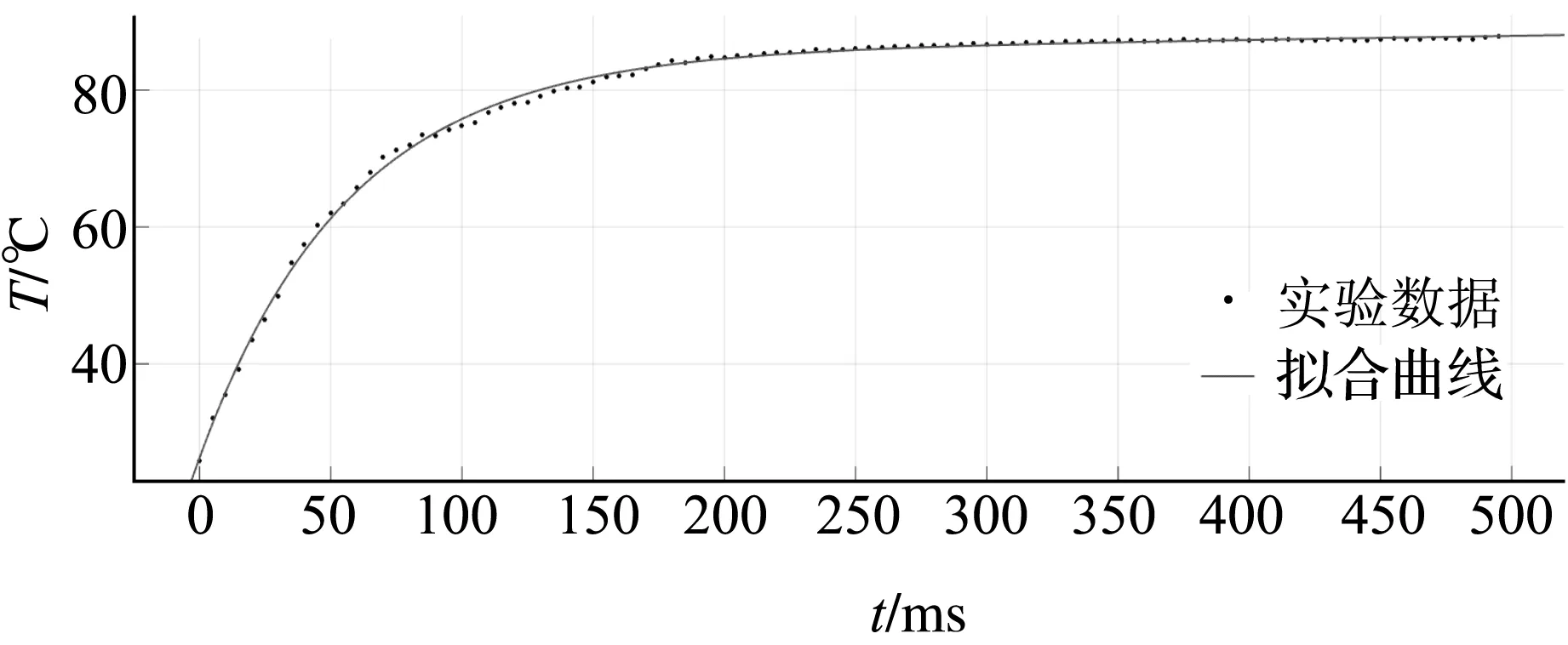
图7 热电偶(Φ0.4)动态响应拟合曲线Figure 7 Dynamic response fitting curve of thermocouple(Φ0.4)

图6为偶丝直径0.1 mm的铜-铜镍K型热电偶动态响应拟合曲线,MATLAB拟合结果如下:

a=87.99(87.83,88.16),

b=1.034e-5(4.233e-6,1.645e-5),

c=-64.72(-65.25,-64.18),

d=-0.061 3(-0.062 25,-0.060 35),

3 理论计算

3.1 集总参数法

内部导热热阻远小于表面换热热阻的非稳态导热体称为集总体,任意时刻导热体内部各点温度接近均匀.此时导热体的温度分布只随时间变化,而不随空间变化,因此又称之为零维问题.其优点是可以处理任意形状的物体.

若忽略物体内部导热热阻,认为物体任意时刻内部温度接近均匀,则温度分布只随时间变化,这种简化分析方法称为集总参数法[10].

对于体积为V(m3),表面积为A(m2),初始温度为T0(℃)的热电偶球形测量端,在初始时刻,将其快速置于温度恒为Τ∞(℃)的流体,此时热量主要以对流换热的形式从流体传输到热电偶的球形测量端表面.球形测量端与流体间的表面换热系数h(W·m-1·K-1)、球形测量端密度ρ(kg·m-3)、球形测量端导热系数λ(W·m-1·K-1)、球形测量端比热容c(J·kg-1·K-1)为常量,根据集总参数法确定温度随时间的依变关系

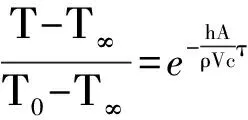
(8)

令

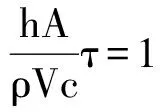
(9)

求得的时间τ为热电偶的时间常数τc,反应了物体对温度变化的动态响应的快慢.根据式(9)可得[11]

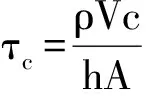
(10)

3.2 集总参数法适用条件

Bi数的物理意义为物体内部导热热阻与物体表面对流换热热阻之比.Bi数越小,则内热阻越小或外热阻越大,此时集总参数法的计算结果越接近实际情况.

对于平板、圆球、圆柱来说,如果Bi数满足

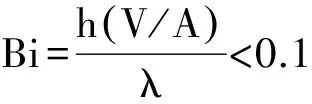
(11)

则用集总参数法分析非稳态导热问题的误差不超过5%[12],这是与物体几何参数有关的一个无量纲常数.如果Bi数远小于0.1,则可认为任意时间物体内的温度分布都趋于均匀一致.

3.3 时间常数理论值计算

为了计算热电偶测量端的等效表面积和等效体积,可将两支铜-铜镍K型热电偶的测量端等效为一个规则球形,球形测量端的几何参数如表2.其中偶丝直径0.1 mm的铜-铜镍K型热电偶用Φ0.1表示,偶丝直径0.4 mm的铜-铜镍K型热电偶用Φ0.4表示.

表2 热电偶测量端几何参数

Table 2 Geometric parameters of thermocouple measurement

测量端半径/mm测量端表面积/mm2测量端体积/mm3Φ0．10．244Φ0．10．749Φ0．10．061Φ0．40．650Φ0．45．309Φ0．41．150

铜-铜镍K型热电偶热物性参数,如表3.

表3 热电偶热物性参数

铜-铜镍K型热电偶的测量端由两种不同材料的导线焊接而成,可取两种不同材料的平均值.由于RTS-40A制冷恒温槽内部恒温介质为水,内部具有搅拌器,可使水进行受迫运动并与两支铜-铜镍K型热电偶的测量端进行强制对流换热,且本测试系统选用的两支铜-铜镍K型热电偶的测量端都极其微小,所以两支铜-铜镍K型热电偶的测量端与RTS-40A制冷恒温槽恒温介质的对流换热系数取水强制对流换热系数经验值区间h=1 000～15 000/(W·m-2·K-1)[13]的最大值,结果如表4.

表4 热电偶测量端热物性参数

Table 4 Thermal physical parameters of thermocouple measurement

对流换热系数/(W·m-2·K-1)密度/(kg·m-3)比热/(J·kg-1·K-1)导热系数/(W·m-1·K-1)150008665400408．92

首先判断两支铜-铜镍K型热电偶的时间常数能否采用集总参数法进行理论计算,将水强制对流换热系数的经验值区间h=1 000～15 000/(W·m-2·K-1)[13]带入下面公式,得出

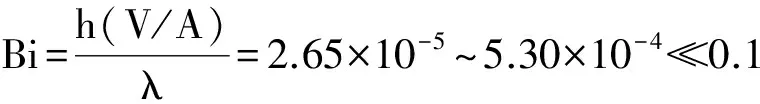
(12)

根据式(11)与(12),可以采用集总参数法进行理论计算.

根据式(10),得出偶丝直径0.1 mm的铜-铜镍K型热电偶的时间常数的理论计算值为

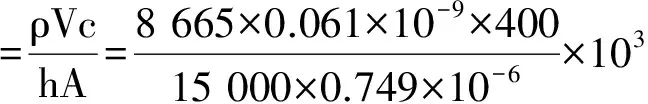
偶丝直径0.4 mm的铜-铜镍K型热电偶的时间常数的理论计算值为

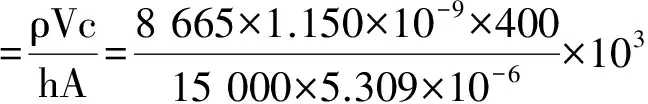
3.4 结果分析

将两支铜-铜镍K型热电偶时间常数第三次实验测试值与理论计算值进行比较.

可得偶丝直径0.1 mm的铜-铜镍K型热电偶时间常数实验测试值与理论计算值的绝对误差为

|16.82-18.8|=1.98.

偶丝直径0.4 mm的铜-铜镍K型热电偶时间常数实验测试值与理论计算值的绝对误差为

|53.70-50.05|=3.65.

可以看出两支铜-铜镍K型热电偶时间常数实验测试值与理论计算值较为接近.且通过MATLAB拟合得出的两支铜-铜镍K型热电偶的函数关系式均符合热电偶动态响应方程形式．这表明,该热电偶时间常数测试系统实验测试数据较为可靠．

4 误差分析

本文设计的热电偶时间常数测试系统使用M12激光对射式光电传感器记录两支铜-铜镍K型热电偶接触RTS-40A制冷恒温槽恒温介质时间点,使得在实验过程中由两支铜-铜镍K型热电偶自身的热惰性所引起的测量滞后误差[14]大大减小.然而该测试系统在实验测试过程中仍会产生其他的误差,影响测量精度.

两支铜-铜镍K型热电偶在插入RTS-40A制冷恒温槽介质之前会有一段行程,在这个过程中空气与RTS-40A制冷恒温槽恒温介质已经开始进行对流换热.所以两支铜-铜镍K型热电偶在插入RTS-40A制冷恒温槽介质之前很短的时间内会受到介质上方温场的影响,导致插入RTS-40A制冷恒温槽介质的瞬间,两支铜-铜镍K型热电偶的初始温度不为室温.

对于RTS-40A制冷恒温槽介质与空气对流换热引起的动态误差,有两种方法可以用来降低它的影响.

一种方法是减少两支铜-铜镍K型热电偶插入RTS-40A制冷恒温槽恒温介质过程的运行时间,如果插入足够迅速,即使两支铜-铜镍K型热电偶吸收热量,它依旧和RTS-40A制冷恒温槽恒温介质温度之差不小于20℃,仍是一个阶跃温度,可以把两支铜-铜镍K型热电偶所升高的温度忽略不计.

另外一种方法是隔离空气和RTS-40A制冷恒温槽恒温介质来减小温场的影响.可在RTS-40A制冷恒温槽恒温介质上方加一层隔热物质.

5 结语

理论计算热电偶时间常数往往与实际测量值有差别,但可通过实验测试的方式获得热电偶时间常数.

本文设计了一种热电偶时间常数测试系统,包括恒温槽、热电偶、激光对射式光电传感器、数据采集卡和计算机.由于激光对射式光电传感器的响应时间小于热电偶的响应时间,因此利用激光对射式光电传感器记录热电偶接触恒温槽恒温介质时间点,可以极大减少热电偶自身的热惰性所引起的测量滞后误差．

将热电偶时间常数的实验测试值与理论计算值进行了比较,绝对误差较小,结果较为接近,且通过MATLAB对热电偶的温度数据进行拟合,得出两支热电偶的函数关系式均符合热电偶动态响应方程形式.这就表明,该热电偶时间常数测试系统较为可靠．

[1] 蔡锡松.对热电偶温度计量误差与修正方法的分析[J].科技资讯,2011(17):113. CAI X S. Analysis on the error of thermocouple temperature measurement and correction method[J].Science & Technology Information,2011(17):113.

[2] 杨述平.激光调制法的热电偶时间常数测量[J].中北大学学报(自然科学版),2007,28(3):246-250. YANG S P. Time constant measurement of thermocouple by modulated laser[J].Journal of North University of China(Natural Science Edition),2007,28(3):246-250.

[3] 吕鹏飞,裴东兴,沈大伟.基于K型热电偶的瞬态测温技术的研究[J].传感技术学报,2014,27(6):775-780. LV P F,PEI D X,SHEN D W. The research of transient thermometry technology based on K-style thermocouple[J].Chinese Journal of Sensors and Actuators,2014,27(6):775-780.

[4] 黄亮,郝晓剑,周汉昌.热电偶时间常数测试技术研究[J].传感器世界,2006(9):16-18. HUANG L, HAO X J, ZHOU H C. Measurement techni-que of thermocouple time constant[J].Senser World,2006(9):16-18.

[5] 刘宗瑞,咸婉婷,刘志远.热电偶动态响应测试系统[J].传感器与微系统,2014,33(6):82-85. LIU Z R, XIAN W T, LIU Z Y. Dynamic response testing system of thermocouple[J].Transducer and Microsystem Technologies,2014,33(6):82-85.

[6] 张存芳,李秀芬,薛熊.温度传感器时间常数测试数据的处理方法[J].宇航计测技术,2001,21(2):32-35. ZHANG C F, LI X F, XUE X. Processing method of temperature sensor time constant test data[J].Journal of Astronautic Metrology and Measurement,2001,21(2):32-35.

[7] 吴方,杨新圆,王莉.表面温度传感器时间常数测量方法研究[J].计测技术,2014,34(4):60-62. WU Fang, YANG X Y, WANG L. Study on measuring time constants of surface temperature sensors[J].Metrology & Measurement Technology,2014,34(4):60-62.

[8] 李靖宇.激光对射式光电传感器实现定位车快速精确定位[J].水运工程,2015(4):50-54. LI J Y. Fast and precise train positioning using laser photoelectric sensor[J].Port & Waterway Engineering,2015(4):50-54.

[9] 邓建云.光电传感器在自动控制中的应用[J].电子世界,2012(9):159-160. DENG J Y. Application of photoelectric sensor in automatic control[J].Electronics World,2012(9):159-160.

[10] 陈聪,刘跃军,黄逊青.集中参数法用于储水式电热水器能效测试的试验研究[J].电器,2013(增刊):795-799. CHEN C, LIU Y J, HUANG X Q. Study on lumped p-arameter method for energy efficiency testing of electrical storage water heater[J].China Appliance,2013(suppl):795-799.

[11] 杨世铭,陶文铨.传热学[M].北京:高等教育出版社,2006:117.

[12] 魏克新,杜明星.基于集总参数法的IGBT模块温度预测模型[J].电工技术学报,2011,26(12):79-84. WEI K X. DU M X. Temperature prediction model of IGBT modules based on lumped parameters method[J].Transactions of China Electrotechnical Society,2011,26(12):79-84.

[13] 谭天恩,李伟.过程工程原理[M]．北京:化学工业出版社,2004:112.

[14] 周静伟,黄跃进.热电偶动态响应特性对导热反问题辨识结果的影响[J].中国计量学院学报,1998(1):73-77. ZHOU J W,HUANG Y J. Effect of thermocouple dynamical responsibility on result preicated by IHCP[J].Journal of China University of Metrology,1998(1):73-77.

A thermocouple time constant test system

SUN Hongjian, LI Wenjun, LI Jiaqi, ZHENG Yongjun

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

Time constant is an important indicator used to test the dynamic performance of a thermocouple. In order to measure the dynamic performance of a thermocouple, we designed a thermocouple time constant test system. The system is composed of a thermocouple, a thermostatic bath, a data acquisition card and an opposite type laser photoelectric sensor. In the test process, when the thermocouple contacted the thermostatic bath thermostatic medium to capture the moment by the opposite type laser photoelectric sensor, the temperature data of the thermocouple and the voltage data of the opposite type laser photoelectric sensor were collected by the data acquisition card. The temperature and voltage change curves were displayed and recorded by the data acquisition software. The temperature data of the thermocouple were fitted. The time constant of the thermocouple was tested and the calculated values were compared with the theoretical calculation. Finally, the error of the tested process was analyzed. The results show that the thermocouple time constant test system can greatly reduce the measurement error caused by thermal inertia of thermocouple itself with other micro measurement errors.

thermocouple; data acquisition; opposite type laser; photoelectric sensor; time constant

2096-2835(2017)02-0146-07

10.3969/j.issn.2096-2835.2017.02.003

2016-12-15 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

孙宏健(1993- ),男,吉林省松原人,硕士研究生,主要研究方向为传感器技术.E-mail:785826949@qq.com 通信联系人：李文军,男,副教授.E-mail:liwenjun@cjlu.edu.cn

TP216