气泡在剪切作用下的运动特性研究

刘 依,吕雅琪,聂德明

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

气泡在剪切作用下的运动特性研究

刘 依,吕雅琪,聂德明

(中国计量大学 计量测试工程学院，浙江 杭州 310018)

采用基于自由能模型的格子Boltzmann方法，考虑到毛细管数和气液黏性比的影响，模拟了气泡在剪切作用下的动力特性.结果表明，无论气泡半径大小，总是其长轴被拉伸，中轴和短轴被压缩，且中轴的长度总大于短轴的长度.随着毛细管数的增加或气液黏性比的增大，气泡变形和偏转程度越剧烈.

剪切流场；毛细管数；气液黏性比；格子Boltzmann方法

在化工行业、水利工程、水上运输、水下探测和环境污染物防治等领域中，气泡的动力学特性的研究是人们关注的热点之一[1].气泡处于黏性液体中时，会受到黏性流体的剪切和拉拽，气泡发生变形或破裂，使得周围流场也会发生相应变化.因此研究气泡在剪切作用下的运动特性，建立准确的预测模型，对工业设备的设计以及安全、高效、可靠运行具有重大的理论意义和工业价值.

在理论分析方面，Taylor[2]最早在1934年对剪切流中单个液滴进行理论分析.Taylor[2]的理论认为液滴的变形是二维轴对称的小变形，即液滴从圆形变成标准椭圆性.同时，引入变形参数描述气泡的变形程度，提出变形参数与毛细管数成线性关系.随着研究的进一步深入，Charles[3]、Cox[4]和Acrivos[5]等学者分别从不同模型出发，从理论上推导了液滴倾斜角与毛细管数的关系.

随着实验条件的提升，有学者开始用实验的方法研究气泡在剪切流中的运动特性.Canedo[6]等人在1993年用实验的方法证明了气泡发生小变形时的变化规律与Taylor[2]的理论相吻合.Rust和Manga[7]在2002年突破了以往实验只关注气泡在低黏性比、低雷诺数下气泡的小变形，关注气泡大变形理论，定量研究毛细管数和偏转角的关系.大量的实验研究表明，在研究气泡和液滴的变形时，两者的理论可以互通.但在研究气泡破裂时，液滴破裂的机理与气泡破裂的机理有所不同，两者不能等同.

实验方法研究虽然能真实客观地反映自然现象，但受制于测量水平，难以分析各参数的影响，无法全面掌握气泡运动规律及机理.而数值模拟方法能克服实验方法的不足，目前已经发展出多种数值方法用于模拟气液两相流动，如Level Set方法[8-10]、VOF (Volume of Fluid) 方法[11-13]和格子Boltzmann方法(LBM)[14-17]等.这些方法在气泡运动的研究中获得了许多成果.Level Set方法[8-10]和VOF方法[11-13]是以连续介质理论为基础，需要求解复杂的非线性方程.而LBM是基于微观尺度上的统计力学Boltzmann方程，在计算中LBM只涉及一系列的碰撞和流过程步骤，对于复杂结构的无滑移边界条件很容易实现，能更合理准确地描述物理条件，因此非常适合涉及界面运动的模拟.近二十几年来已经发展出几种适用于多相流的格子Boltzmann模型，如颜色模型[18]、伪势模型[19]和自由能模型[20].颜色模型[18]和伪势模型[19]在涉及热力学方面计算时遇到很大的限制.而自由能模型[20]引入对流扩散方程来描述气液界面，该方程求解简单，易于实现，且可以较好地与其他热模型结合，因此更加适合气泡运动的模拟和研究.

目前，针对气泡运动的研究主要集中在气泡融合、破裂以及重力作用下上升等方面.气泡在流场剪切下会发生变形或旋转，这对于流体的宏观流动具有重要影响.可以预测，气泡的变形必定与流场条件以及气泡属性有关，这在以往的研究中较为缺乏.因此，本文拟采用Zheng等人[21-22]提出的基于自由能模型的格子Boltzmann方法，在三维情况下探讨剪切流场中气泡的运动特性，研究毛细管数Ca和气液黏性比对气泡形态变化的影响.

1 数值方法

流体运动的Navier-Stokes方程和界面演化方程为

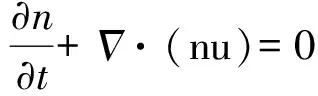
(1)

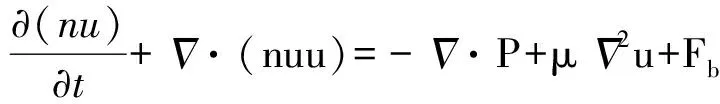
(2)

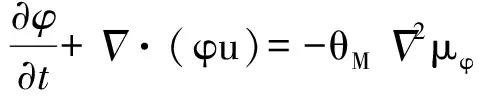
(3)

其中θM是迁移率，P是压力，Fb是体积力.n是半密度和，φ是半密度差(也叫相序参数)，即n=(ρA+ρB)/2，φ=(ρA-ρB)/2.ρA和ρB代表的是流体A和流体B的密度.μφ是化学势能，根据Zheng等人[21]，μφ可以表示为

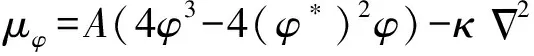
(4)

式(4)中，φ*是与平衡状态相关的常数，即

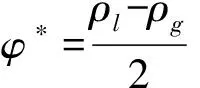
(5)

式(5)中ρl和ρg分别代表液体的密度和气体的密度.系数A定义为

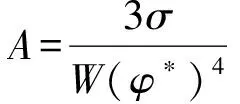
(6)

式(6)中σ为表面张力，W为界面厚度.κ的表达式为

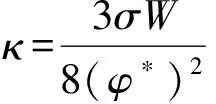
(7)

1.1 连续方程和动量方程的求解

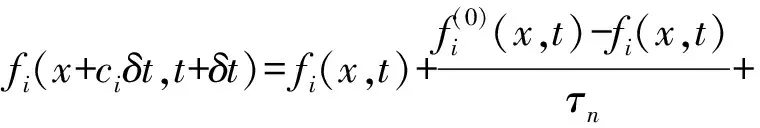
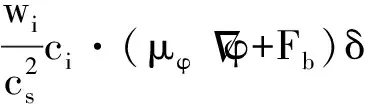
(8)

为了模拟三维的气泡运动，本文采用D3Q15格子模型，其离散速度c方向为

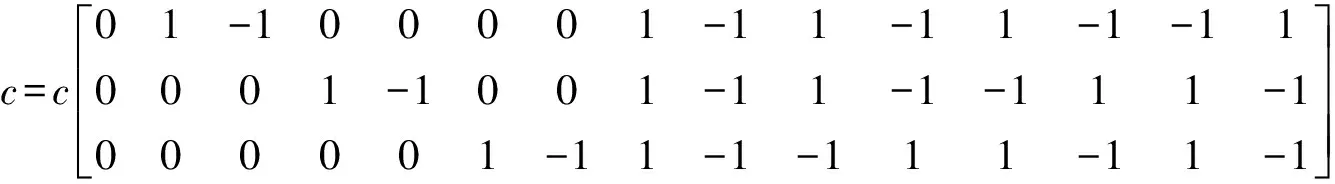
(9)

采用如下所示的平衡态分布函数

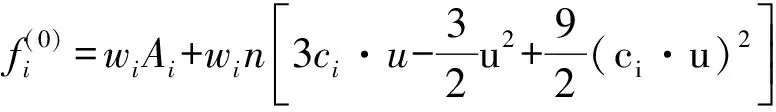
(10)

为了得到式(10)中的系数Ai和权系wi，引入质量、动量和二阶速度矩的守恒关系，即

(11)

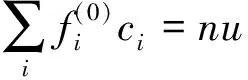
(12)

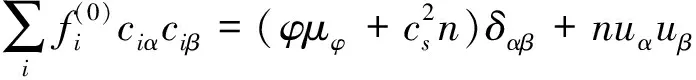
(13)

其中格子速度cs=c2/3，将平衡态分布函数式(10)代入式(11)、(12)以及(13)，考虑D3Q15的格子速度矢量式(9)，可以得到对应的系数Ai和权系数wi的值

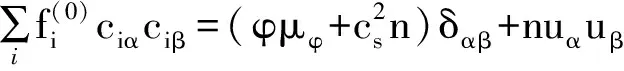
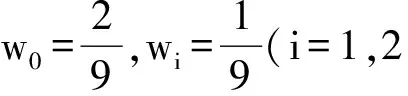
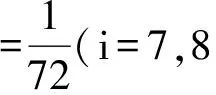
1.2 界面捕捉方程的求解

为了求解界面方程(3)，采用如下形式的格子Boltzmann演化方程[21]

gi(x+ciδt,t+δt)=gi(x,t)+(1-q)·

[gi(x+ciδt,t)-gi(x,t)]+Ωi.

(14)

根据Huang等人[22]，gi的平衡态分布函数为

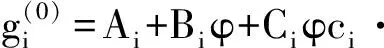
(15)

采用D3Q7模型，其离散的速度方向为

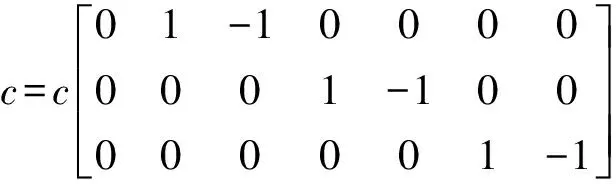
(16)

为了得到式(15)中的系数Ai、Bi和Ci，引入质量、动量和二阶速度矩的守恒关系，即

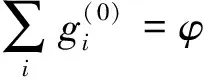
(17)

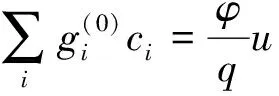
(18)

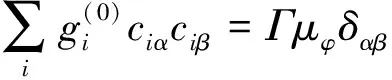
(19)

则可以推得各项系数为

B0=1,Bi=0(i≠0)，

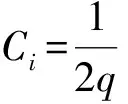
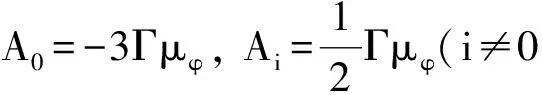
其中Γ与迁移系数相关.

1.3 模型验证

根据Jacqmin[24]，关于球形气泡的相序参数即气液界面的理论值为

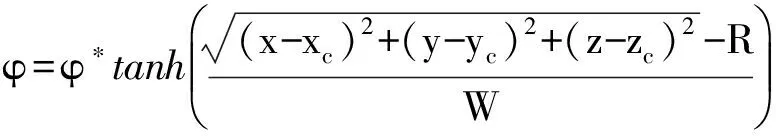
(20)

式(20)中xc、yc和zc是气泡中心的坐标值.式(20)可以用来表示气液的界面曲线.为了验证本文的方法，采用式(20)进行验证.

设置计算区域为N3=64×64×64，表面张力σ=1.0，界面宽度W=3.5.对以下两种情况进行模拟:①气泡半径R=10，ρl=1000，ρg=1；②气泡半径R=15，ρl=500，ρg=1.结果如图1，图1中符号表示的是本文D3Q15对应的数值解，实线和虚线对应的是理论解即式(20).可以看到，本文采用的方法准确地捕捉到了气液的界面曲线.

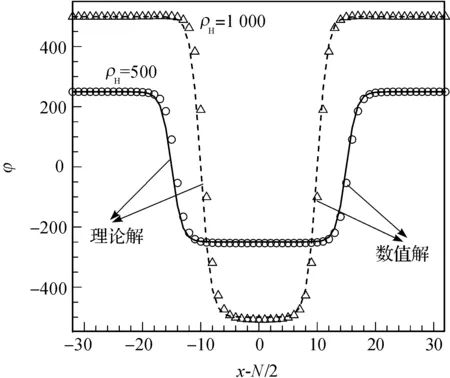
图1 气液界面的数值解与理论解的比较Figure 1 Comparison of analytical solution and numerical results for gas-liquid interface profile

Zheng等人[21]通过研究表明，界面厚度W对模拟的结果有影响，若选取的W较小时会出现明显的误差.我们分别选取W=1.5,2.0,2.5,3.5和4.5，通过计算可以得到气泡内外的压力差Δp.再通过内外压力差和表面张力的平衡方程Δp=2σ/R，可以计算表面张力.计算结果表明随着界面厚度W的增大，计算所得的表面张力逐渐靠近理论值.当W=4.5时，计算值与理论值的误差小于5%，因此在后续的计算中界面厚度均采用W=4.5.

2 计算结果及讨论

初始形状为球形的气泡发生椭球形变形，如图2所示变形后气泡长轴、中轴及短轴的半径分别为R1、R2和R3，定义变形率ε1=(R1-R)/R、ε2=(R2-R)/R和ε3=(R3-R)/R，ε>0为拉伸，ε<0为压缩.图3(a) 、(b)分别为椭球形气泡的正视图和侧视图，定义气泡长轴与x轴的夹角θ为气泡偏转角，定义初始球形气泡的偏转角为45°.

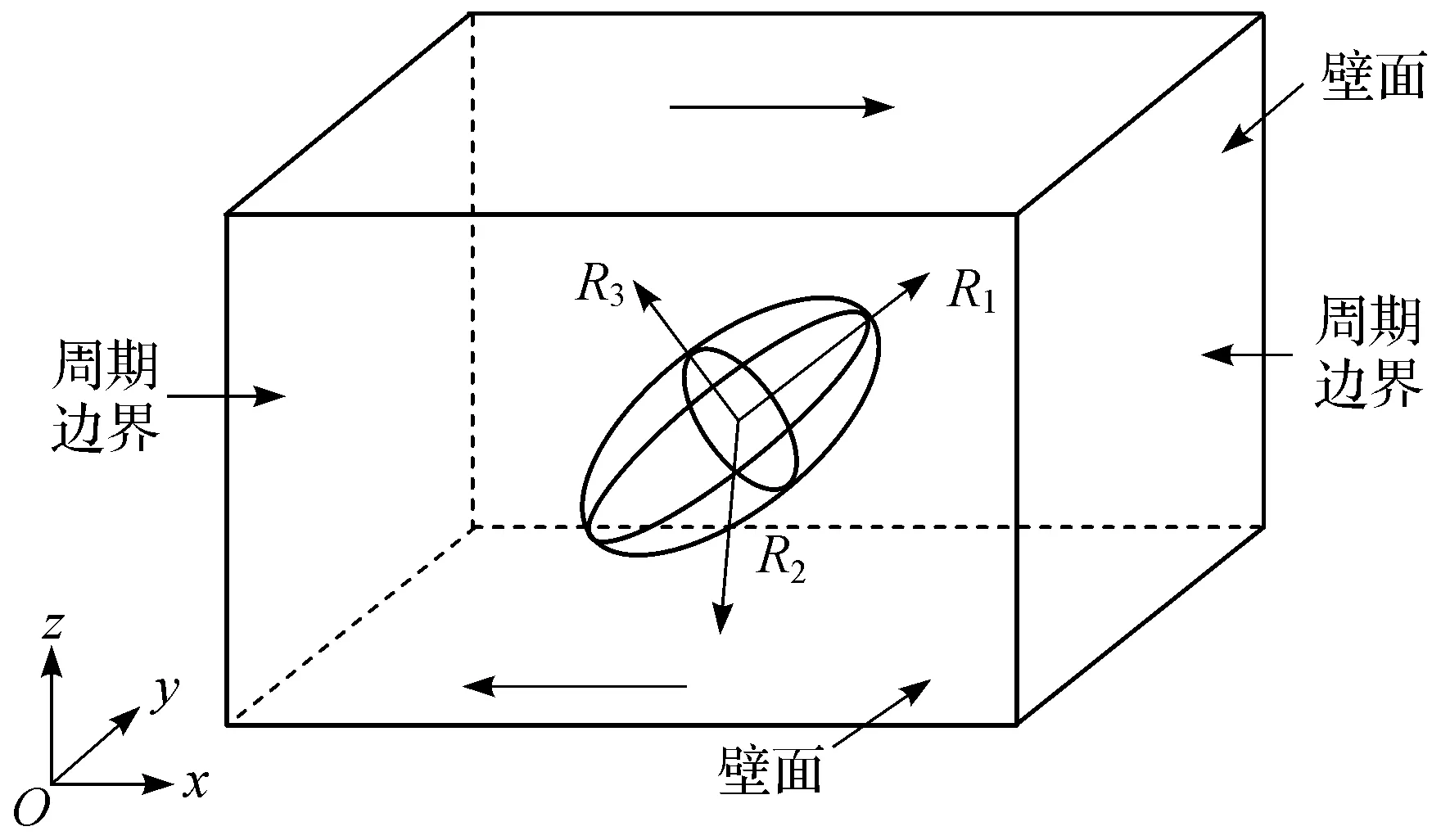
图2 流场示意图和边界条件Figure 2 Geometry and boundary condition

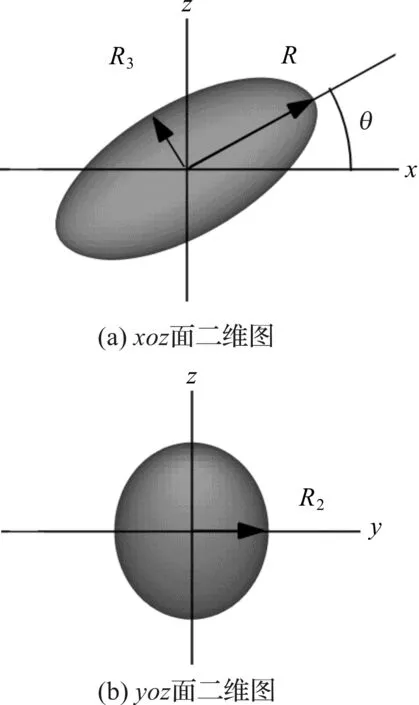
图3 椭球形气泡的正视图和侧视图Figure 3 Front view and side view of ellipsoidal bubble

在剪切流场中，气泡变形是非线性的动力学过程，通常伴随气泡的变形、流体之间的对流和表面张力等复杂的相互作用.在剪切流场中通常用毛细管数Ca和雷诺数Re这两个无量纲量描述流场的运动情况.毛细血管数Ca表征的是流场剪切强度与表面张力之比，流场的剪切力对气泡产生变形拉伸作用，而气泡的表面张力让气泡保持原状，可见Ca数越大，对气泡变形的作用强度越大.

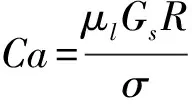
(21)

雷诺数Re表征的是惯性力与黏性力之比，表达式如下:

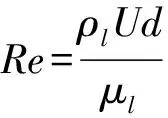
(22)

式(22)中d为气泡初始直径.

计算区域设置为N3=130×100×130，上壁面和下壁面采用速度边界，前壁面和后壁面采用固定壁面边界条件，左边界和右边界采用周期性边界条件.其他参数设置为液体密度ρl=1000，气体密度ρg=1，气泡表面张力σ=0.2，迁移系数Γ=800，无量纲时间因子τn=0.6、τφ=0.7以及界面厚度W=4.5.在格子Boltzmann方法中，液体黏性是无量纲时间因子的函数，关系如下:

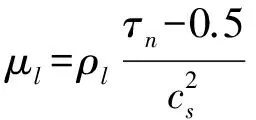
(23)

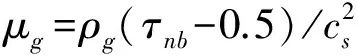
计算结果将分三种情况讨论.

2.1 不同初始半径的气泡

为了研究气泡大小对气泡变形的影响，设上壁面速度为U=0.013，下壁面速度为U=-0.013，气液黏性比μl/μg=1000，分别取气泡半径R=8、10、12和14.计算结果表明，无论气泡半径大小，气泡在x、y和z方向的速度和位移均为零.

图4 (a)～(h)分别表示气泡半径为8、10、12和14时，气泡在xoz面和yoz面上随时间步变化的示意图.从图中可以看出，气泡初始形状为圆球形，在剪切流场的作用下，气泡在x方向受到上下壁面朝相反运动方向的拉伸，从xoz面上看，圆形气泡逐渐变为椭圆形并于x轴成一定夹角.从yoz面上看，圆形气泡逐渐变为与z轴平行的椭圆形.随着时间步推移，气泡长轴拉伸越来越大，中轴和短轴压缩越来越明显，且短轴的压缩强度比中轴的压缩强度强.当气泡达到稳定状态时，气泡半径越大，气泡变形越强烈，偏转角越小，气泡倾斜程度越明显.下面定量分析气泡初始半径分别对气泡最终稳定时的长轴、中轴、短轴的变形率和偏转角的影响.

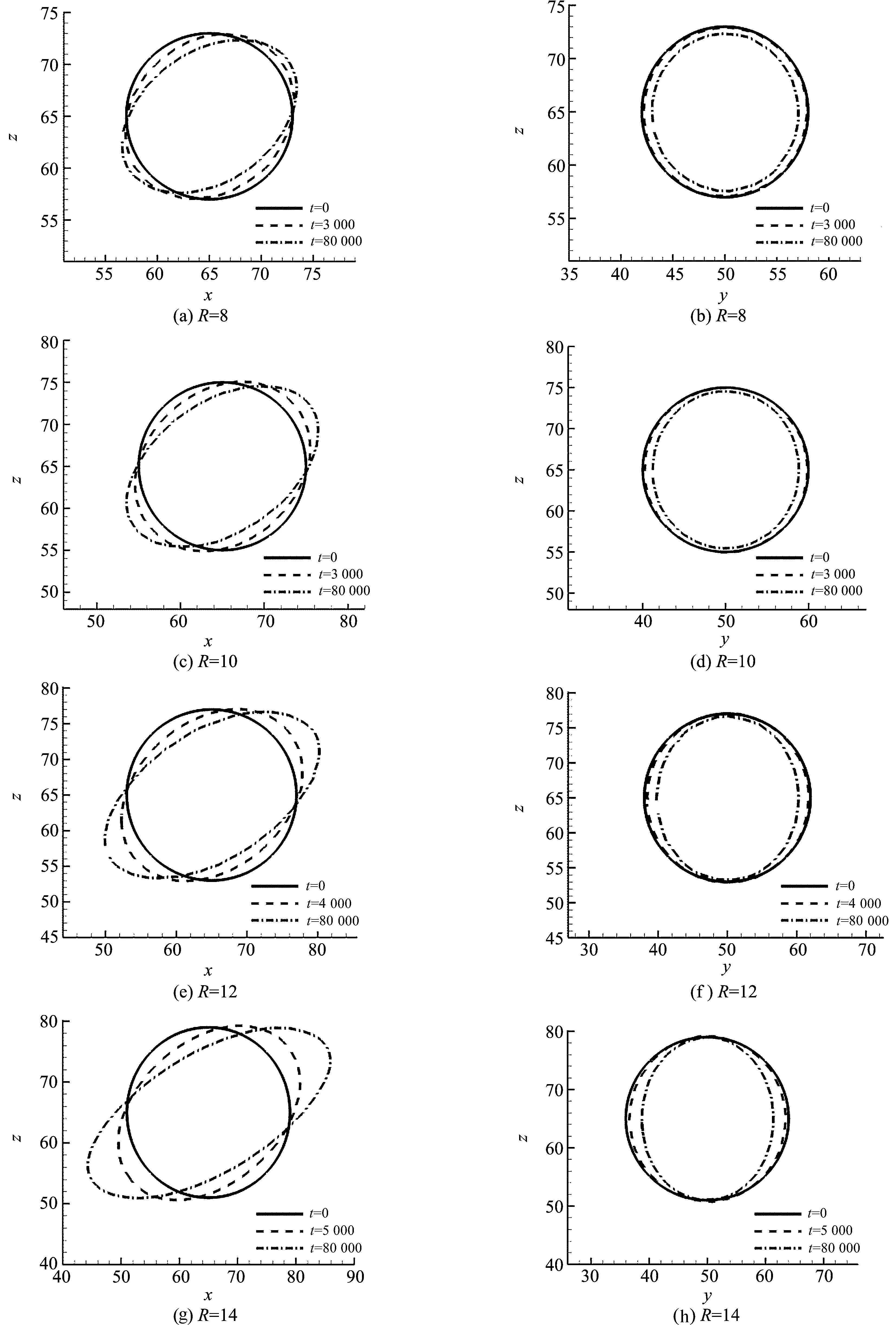
图4 不同半径气泡随时间步的变形形态正视图Figure 4 Time evolution of bubble shape at different radius in front view

图5描述的是不同初始半径的气泡长轴的变形率随时间步的变化，长轴的变形率从0开始增长为正值，说明长轴被拉伸.且随着初始半径的增大，拉伸率也在增大，说明初始半径越大，气泡长轴被拉伸的幅度也越大.图6描述的是不同初始

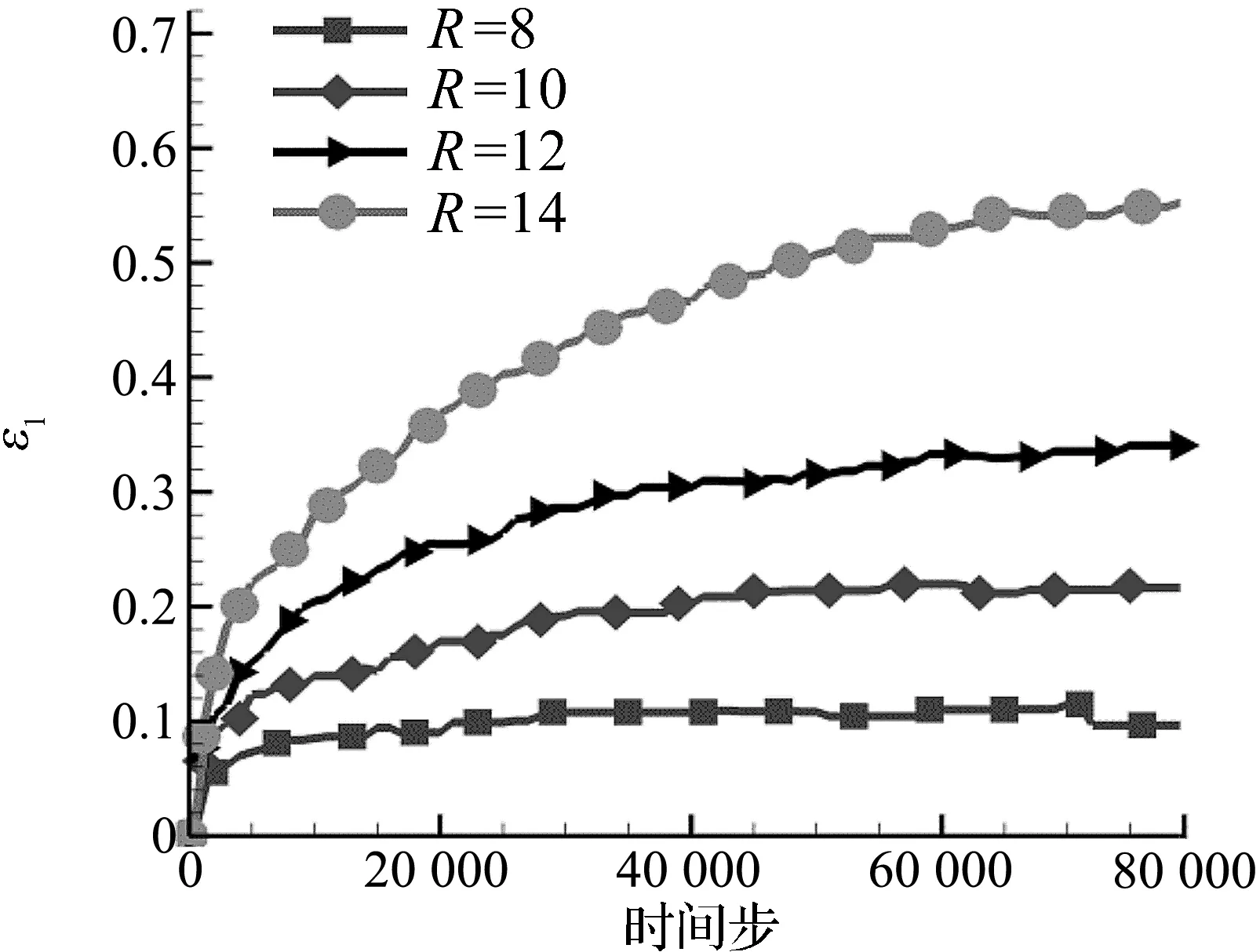
图5 不同半径气泡的长轴随时间步的拉伸率Figure 5 Time evolution of major axis stretch ratio at different radius

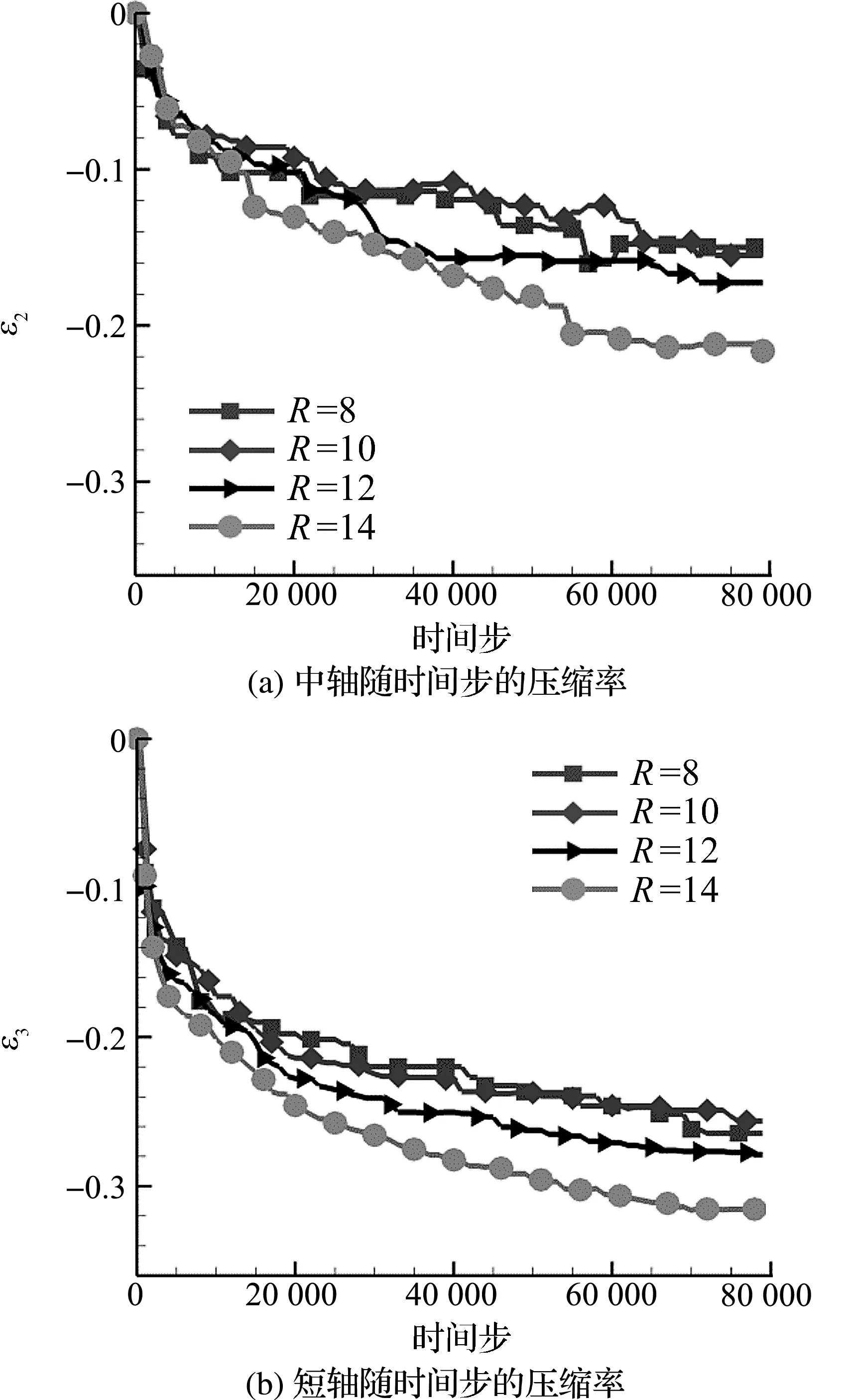
图6 不同半径气泡的中轴和短轴随时间步的压缩率Figure 6 Time evolution of mean axis and minor axis compression ratio at different radius

半径的气泡中轴和短轴的变形率随时间步的变化，中轴和短轴的变形率从0开始递减为负值，说明中轴和短轴被压缩.

图7描述的是不同初始半径气泡在剪切流场稳定时的偏转角，定义初始角度为45°，随着时间步的增加，偏转角逐渐减小最后趋于稳定.但是若气泡半径较小(R=8)，偏转角呈震荡趋势，最后趋于稳定.

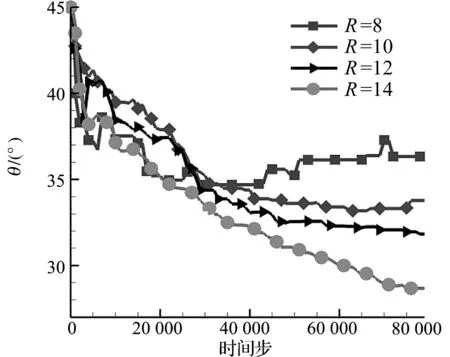
图7 不同气泡半径下对应的偏转角Figure 7 Time evolution of deflection angle at different radius

可见随着气泡半径的增加，即Ca数的增加，气泡变形率的绝对值越来越大，气泡变形强度也越大，但气泡偏转角越来越小.

2.2 不同剪切强度流场下的气泡

为了研究不同剪切强度流场对气泡变形的影响，固定气泡半径R=12，气液黏性比μl/μg=1000，上壁面速度和下壁面速度分别取为U=±0.003、U=±0.005、±0.007和±0.010，即流场的剪切强度Gs分别为2.3×10-5(1/s)、3.8×10-5(1/s) 、5.4×10-5(1/s)和7.7×10-5(1/s).图8描述的是在不同剪切强度下气泡稳定时的xoz面二维形态，随着剪切强度的增强，偏转角越小，倾斜程度越大.下面定量分析剪切流场强度分别对气泡最终稳定时的长轴、中轴、短轴的变形率和偏转角的影响.

图9描述的是不同剪切流场强度下气泡长轴的变形率随时间步的变化，当剪切流场强度较小时，剪切流场强度Gs为2.3×10-5(1/s)，长轴的变形率在数值0上下小幅波动，最终稳定为0，即长轴没有被拉伸也没有被压缩，而是保持与初始半径一样的长度.当剪切流场强度增大时，长轴会被拉伸.且随着剪切强度的增大，拉伸率也在增大，气泡长轴被拉伸的幅度也越大.

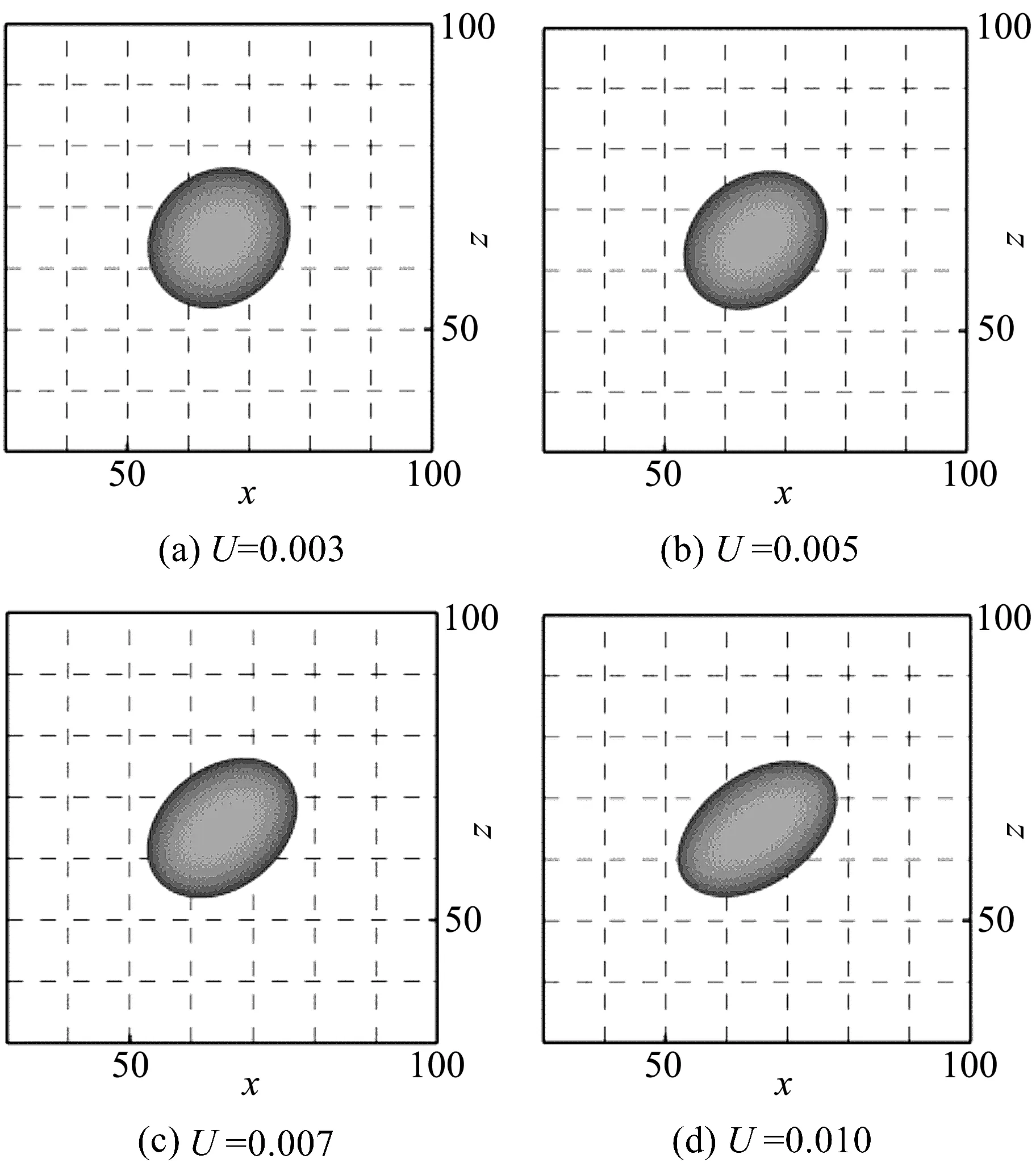
图8 不同剪切流场下气泡的最终形态Figure 8 Final deformed shapes at different sheer rate

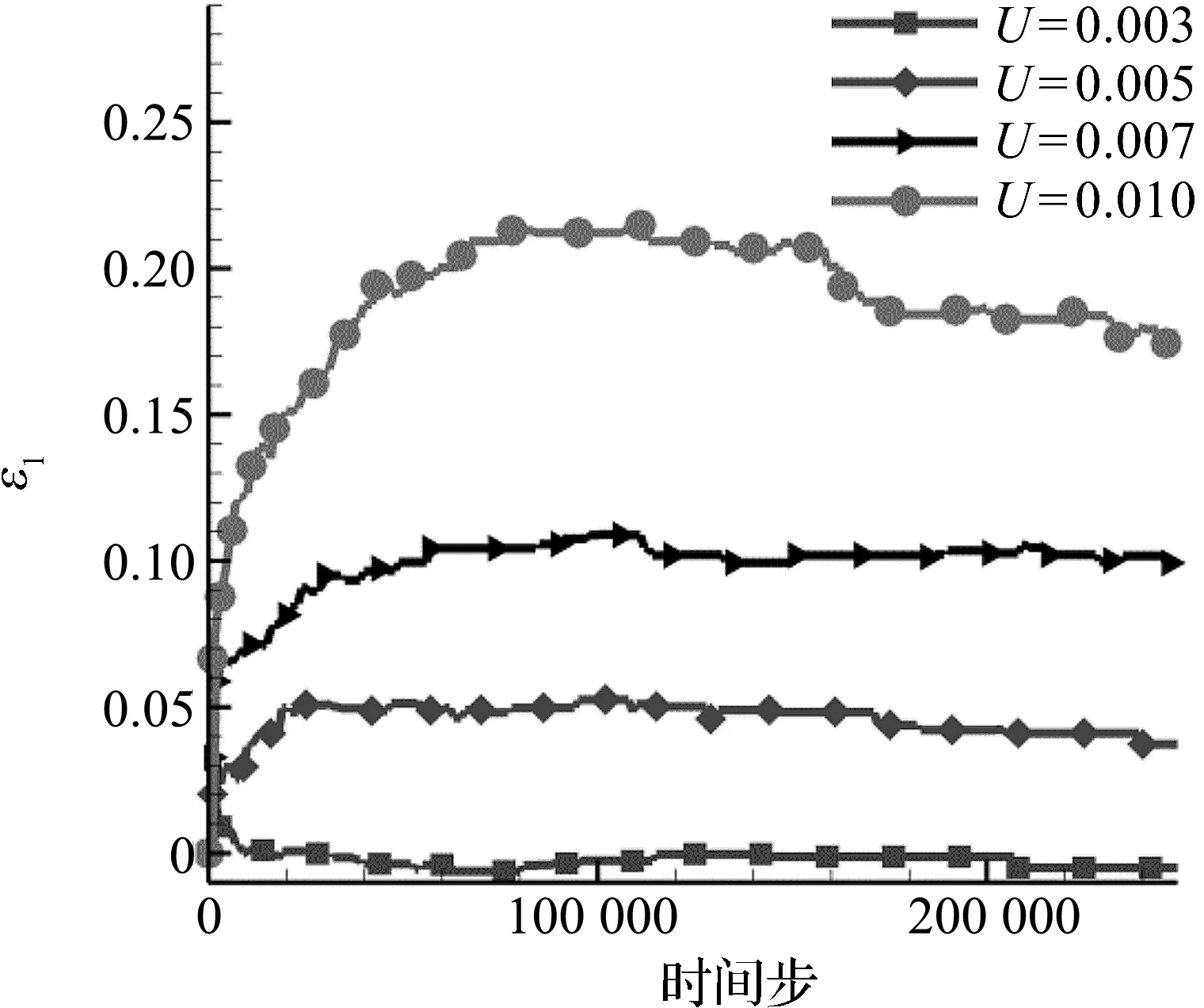
图9 不同剪切流场强度下气泡长轴随时间步的拉伸率Figure 9 Time evolution of major axis stretch ratio at different sheer rate

图10描述的是不同剪切流场强度下气泡中轴和短轴的变形率随时间步的变化，可见中轴和短轴被压缩.随着剪切流场强度的增大，压缩率也在增大，压缩程度更剧烈.

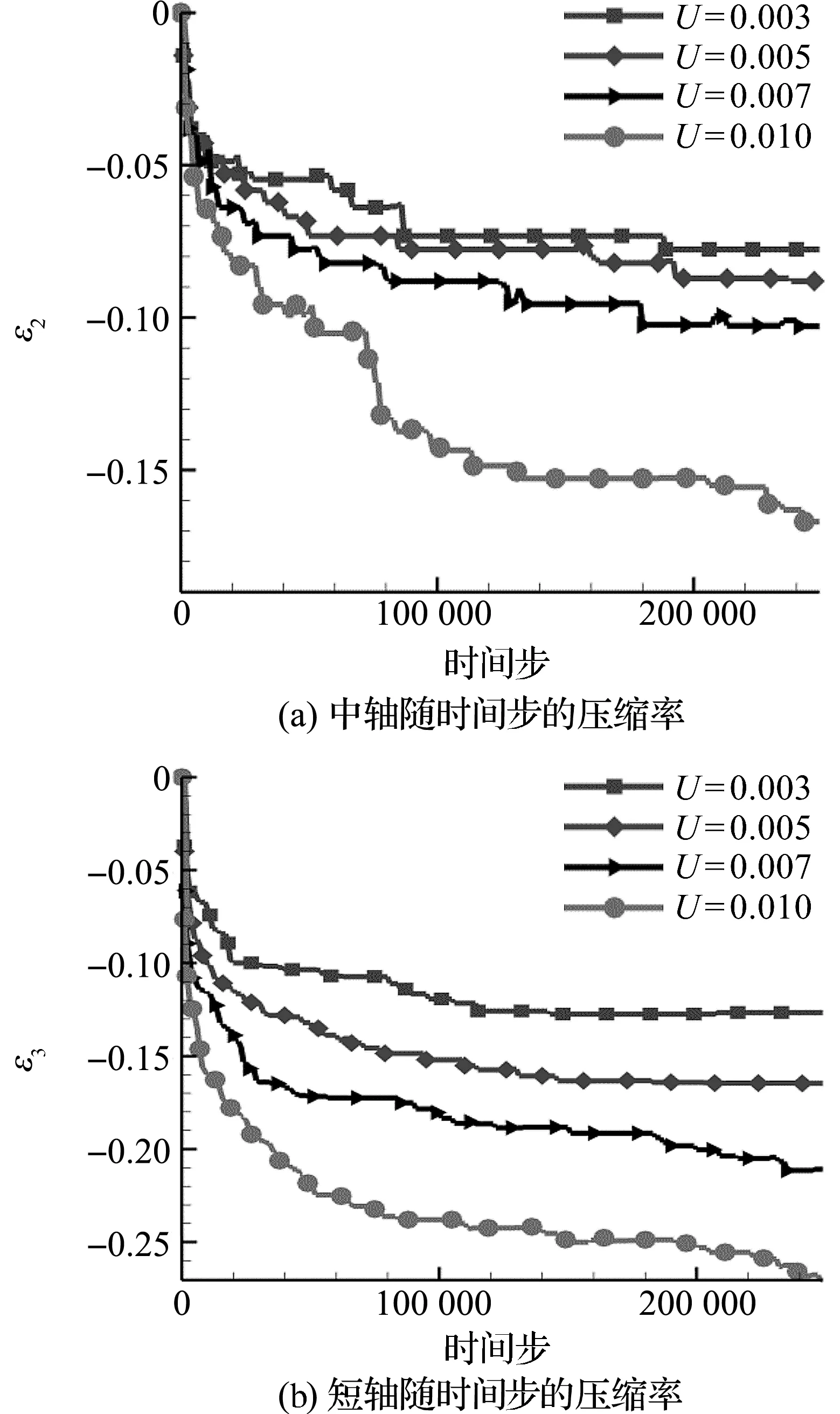
图10 不同剪切流场强度下气泡的中轴和短轴随时间步的压缩率Figure 10 Time evolution of mean axis and minor axis compression ratio at different sheer rate

从数据中我们可以看出，随着流场剪切程度增强，即随着Ca数的增加，气泡最终稳定时的偏转角在减小，即偏转程度增强.结合2.1的四个算例和2.2的四个算例，Ca数与气泡稳定时最终偏转角的关系如图11所示.Stefano等人[25]用实验的方法测量Ca<0.3时，气泡稳定时最终偏转角，认为Ca与偏转角呈线性关系.LBM数值模拟的数据显示，随着Ca数的增大，偏转角减小，模拟的结果与实验值的趋势一致.最大的误差出现在Ca=0.23时，误差为6.6%，误差在可接受的范围内.

2.3 不同气液黏性比的气泡

为了研究不同气液黏性比对气泡变形的影响，固定上壁面速度为U=0.013，下壁面速度为U=-0.013，气泡半径R=12，气液黏性比μl/μg分别取20、50、100和500.下面将定量分析不同气液黏性比对气泡变形及偏转的影响.

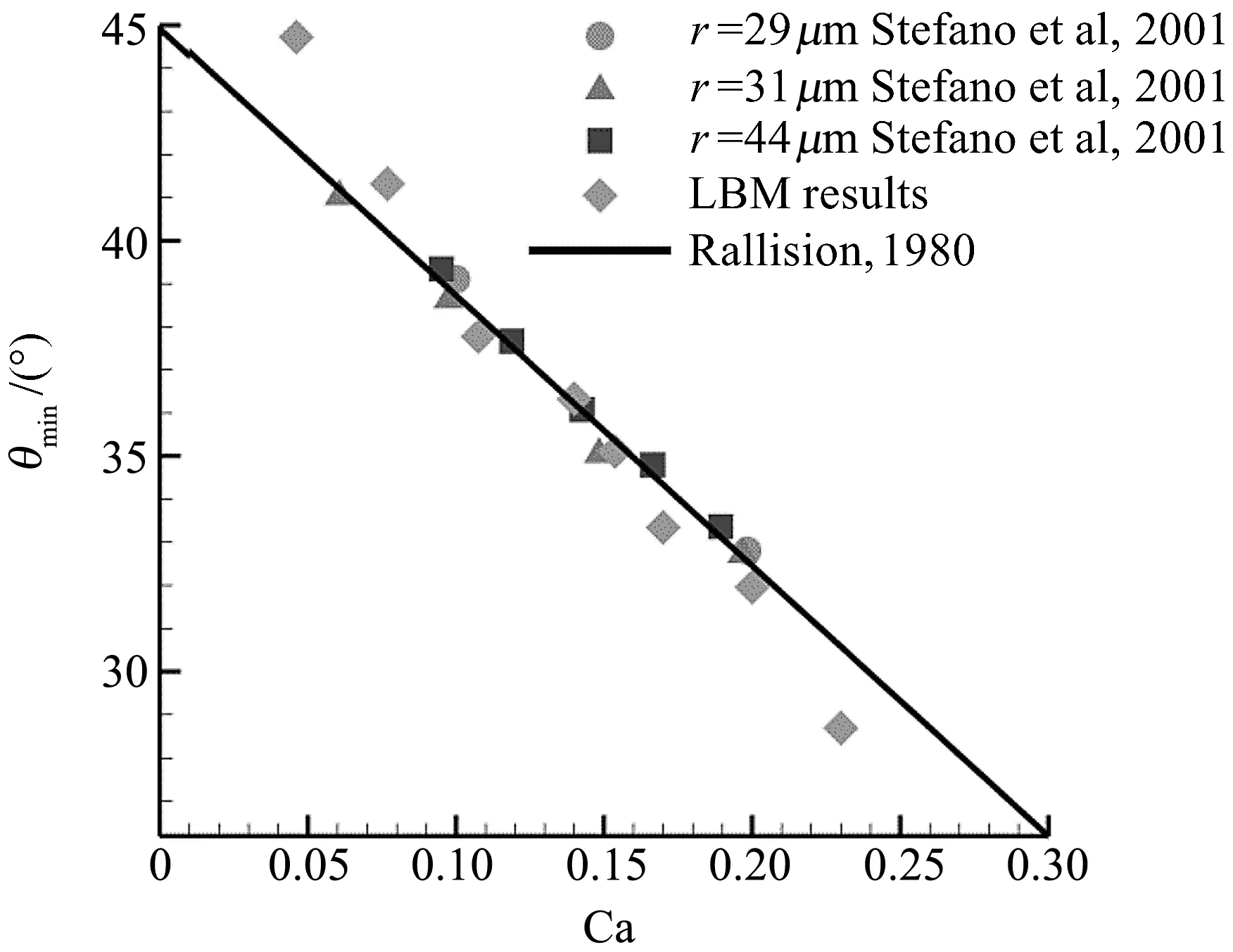
图11 Ca与气泡稳定时偏转角的关系Figure 11 Linear relationship between Ca and deflection angle

不同气液黏性比下气泡长轴的拉伸率，如图12.拉伸率曲线的趋势与长轴长度变化的趋势是一致的.当气液黏性比小于50时，气泡长轴拉伸率随时间步先增加后减小，呈往复振荡后趋于稳定值.当气液黏性比大于50时，气泡长轴拉伸率随时间步增加趋于稳定值.从图中可以看出，气液黏性比越大，气泡变形稳定后气泡长轴的拉伸率越大，气泡的形变程度越明显.图13描述的是不同气液黏性比下气泡中轴和短轴的压缩率.气泡中轴和短轴的压缩率变化趋势相似，当气液黏性比较小时，压缩率随时间步出现往复增加最后稳定的变化趋势.当气液黏性比大于100时，气泡中轴和短轴的压缩率随时间步逐渐增加最后稳定.无论气液黏性比大小，短轴的压缩率比中轴的压缩率大，变形程度更剧烈.

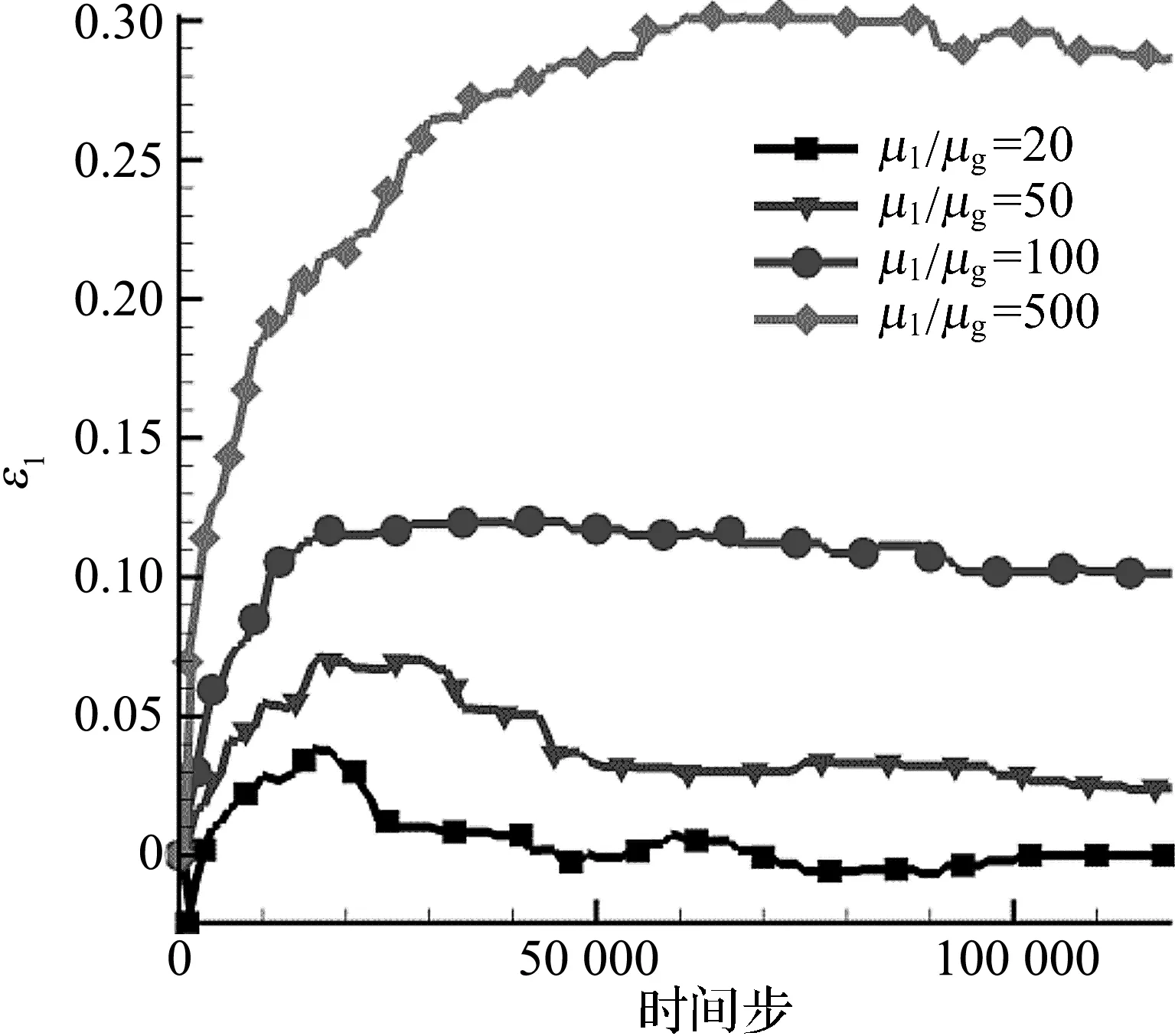
图12 不同气液黏性比下气泡的长轴随时间步的拉伸率Figure 12 Time evolution of major axis stretch ratio at different liquid-gas viscosity ratio

图13 不同气液黏性比下气泡的中轴和短轴随时间步的压缩率Figure 13 Time evolution of mean axis and minor axis compression ratio at different liquid-gas viscosity ratio

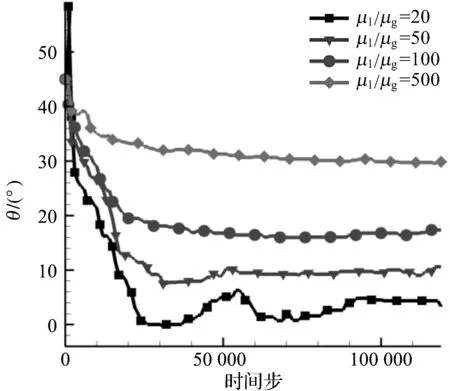
图14 不同气液黏性比下气泡对应的偏转角Figure 14 Time evolution of deflection angle at different liquid-gas viscosity ratio

图14描述的是不同气液黏性比下气泡在剪切流场稳定时的偏转角，定义初始角度为45°，随着时间步的增加，偏转角逐渐减小最后趋于稳定.若气液黏性比较小，如图所示μl/μg=20和μl/μg=50时，气泡的偏转角有小幅振荡，最后趋于稳定.

3 结 语

本文主要研究球形气泡在剪切流场中发生椭球形变形的过程，研究毛细管数Ca与气液黏性比μl/μg对球形气泡变形形态的影响.毛细管数Ca与气泡半径和流场剪切强度相关，即分别研究气泡半径、流场剪切强度和气液黏性比这三个影响量对球形气泡变形形态的影响，得出如下结论:

1)对于不同初始半径的气泡，初始半径越大，气泡变形和偏转程度越剧烈.无论气泡半径大小，总是长轴被拉伸，中轴和短轴被压缩，且中轴的长度总大于短轴的长度.

2)对于不同剪切强度流场下的气泡，流场剪切程度越强，气泡变形和偏转程度越剧烈.

3)随着Ca数的增加，气泡偏转角在减小.本文计算的算例Ca数值范围在0.05～0.23，与实验结果在Ca<0.3时，Ca数与偏转角呈线性递减关系相吻合.

4)对于不同气液黏性比的气泡，随着气液黏性比的增大，气泡变形和偏转程度越剧烈.

[1] 甘延标.多相流系统的格子玻尔兹曼方法与研究模拟[D].北京:中国矿业大学,2012. GAN Y B. The lattice Boltzmann Method of Mutiphase Flow System and Simulation Research[D]. Beijing: China University of Mining and Technology,2012.

[2] TAYLOR G I. The deformation of emulsions in definable fields of flow[J]. Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Science,1934,146(858):501-523.

[3] CHARLES E, CHAFFEY C E, BRENNER H. A second-order theory for shear deformation of drops[J]. Journal of Colloid and Interface Science,1967,24(2):259-269.

[4] COX R G. The deformation of a drop in a general time-dependent fluid flow[J]. Journal of Fluid Mechanics,1969,37(3):601-623.

[5] ACRIVOS A. The breakup of small drops and bubbles in shear flows[J]. Annals of The New York Academy of Sciences,1983,404:1-11.

[6] CANEDO E L, FAVELUKIS M, TADMOR Z, et al An experimental study of bubble deformation in viscos liquids in simple shear flow[J]. Chemical Engineering Journal,1993,39(4):553-559.

[7] RUST A C, MANGA M. Bubble shapes and orientations in low Re simple shear flow[J]. Journal of Colloid and Interface Science,2002,249(2):476-480.

[8] 李彦鹏, 张乾隆, 白博峰. 竖直通道内相邻气泡对上升的直接数值模拟[J]. 热能动力工程,2007,22(4):375-379. LI Y P, ZHANG Q L, BAI B F. Direct numerical simulation of bubble rising in vertical channel[J]. Journal of Engineering for Thermal Energy and Power,2007,22(4):375-379.

[9] 陈菲, 张梦萍, 徐胜利. 运动激波和气泡串相互作用的初步数值模拟[J].计算物理,2004,21(5):443-448. CHEN F, ZHANG M P, XU S L. Preliminary numerical simulation of interaction between moving shock wave and bubble string[J]. Computational Physics,2004,21(5):443-448.

[10] SUSSMAN M, FATEMI E, SMEREKA P, et al. An improved level set method for incompressible two-phase flows[J]. Comput Fluids,1998,27:663-680.

[11] PILLIOD J E, PUCKETT E G. Second-order volume-of-fluid algorithms for tracking material interfaces[J]. Journal of Computational Physics,2004,199:465-502.

[12] 李维仲, 赵大勇, 陈贵军. 竖直流道宽度对气泡运动行为影响的数值模拟[J].计算力学学报,2006,23(2):196-201. LI W Z, ZHAO D Y, CHEN G J. Numerical simulation of the influence of vertical channel width on bubble motion[J]. Journal of Computational Mechanics,2006,23(2):196-201.

[13] 张淑君, 吴锤结. 气泡之间相互作用的数值模拟[J].水动力学研究与进展：A辑,2008,23(6):681-686. ZHANG S J, WU C J. Numerical simulation of bubble interaction[J]. Research and Development of Hydrodynamics A,2008,23(6):681-686.

[14] 孙涛,李维仲,杨柏丞,等.气泡群上升过程相互作用的格子Boltzmann三维数值模拟[J].化工学报,2013(5):1586-1591. SUN T, LI W Z, YANG B C, et al. Three dimensional numerical simulation of the interaction of bubble group rising process with lattice Boltzmann[J]. Journal of Chemical Engineering,2013(5):1586-1591.

[15] 曾建邦, 李隆键, 蒋方明. 气泡成核过程的格子Boltzmann方法模拟[J]. 物理学报,2013,62(17):176401. ZENG J B, LI L J, JIANG F M. Lattice Boltzmann si mulation of bubble nucleation process[J]. Acta Physica Sinica,2013,62(17):176401.

[16] CHENG M, HUA J, LOU J. Simulation of bubble-bubble interaction using a lattice Boltzmann method[J]. Comput Fluids,2010,39:260-270.

[17] 陈荣前,聂德明.格子玻尔兹曼模型的图像去噪方法[J].中国计量大学学报,2016,27(3):345-349. CHEN R Q, NIE D M. Image denoising method based on lattice Boltzmann model[J]. Journal of China University of Metrology,2016,27(3):345-349.

[18] GUNSTENSEN A K, ROTHMAN D H, ZALESKI S, et al. Lattice Boltzmann model of immiscible fluid[J]. Physical Review A,1991,43:4320-4327.

[19] SHAN X, CHEN H. Lattice Boltzmann model for simulating flows with multiple phases and components[J]. Physical Review E,1993,47(3):2557-2562.

[20] SWIFT M R, OSBORNE W, YEOMANS J M. Lattice Boltzmann simulation of nonideal fluids[J]. Physical Review Letters,1995,75:830-833.

[21] ZHENG H W, SHU C, CHEW Y T. A lattice Boltmann model for multiphase flows with large density ratio[J].Journal of Computational Physics,2006,218:353-371.

[22] HUANG H B, ZHENG H W, LU X Y, et al. An evaluation of a 3D free-energy-based lattice Boltzmann model for multiphase flows with large density ratio[J]. International Journal for Numerical Methods in Fluids,2010,63:1193-1207.

[23] GUPTA A, KUMAR R. Lattice Boltzmann simulation to study multiple bubble dynamics[J]. International Journal of Heat and Mass Transfer,2008,51:5192-5203.

[24] JACQMIN D. Calculation of two-phase Navier-Stokes flows using phase-field modeling[J]. Communications in Computational Physics,1999,155:96-127.

[25] STEFANO G, FRANCESCO G. Drop shape under slow steady shear flow and during relaxation. Experimental results and comparison with theory[J]. Rheologica Acta,2001,40(2):176-184.

Numerical research on bubble motion in shear flow

LIU Yi, LYU Yaqi, NIE Deming

(College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

The deformation dynamic characteristic of single bubble in shear flow was simulated by using the Boltzmann method based on the free energy model. Results show that the main axis of the bubble is always stretched while the mean axis and the minor axis are compressed when the bubble is subjected to shear flow. Furthermore, with the increase of the capillary number or the liquid-gas viscosity ratio, the deformation and deflection of bubble becomes severe.

shear flow; capillary number; liquid-gas viscosity ratio; lattice Boltzmann method

2096-2835(2017)02-0159-10

10.3969/j.issn.2096-2835.2017.02.005

2017-03-02 《中国计量大学学报》网址：zgjl.cbpt.cnki.net

浙江省自然科学基金资助项目(No. LY15A020004).

刘依(1992-)，女，浙江省嘉兴人，硕士研究生，主要研究方向为两相流.E-mail:liuyi19921101@163.com 通信联系人：聂德明，男，教授. E-mail: nieinhz@cjlu.edu.cn

O359

A