穷则变，变则通

◇陶 锋

穷则变，变则通

◇陶 锋

在学习圆锥体积计算时，有的学生认为，因为三角形ABC的面积等于长方形ABCD面积的，以AB为轴旋转一周，所得到的圆柱和圆锥等底等高，所以，圆锥的体积是等底等高的圆柱体积的。（如图1）

我首先肯定学生能用运动的眼光去看立体图形，接着和学生探究三角形ABC旋转后得到的圆锥与三角形ACD旋转后得到的空间是否相等。观察与实验是归纳和判断的直接基础，我先请同学们在图1的基础上画出旋转后立体图形的样子。（如图2）

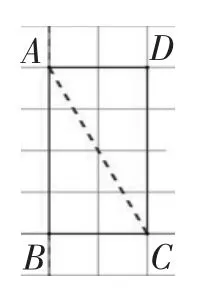
图1

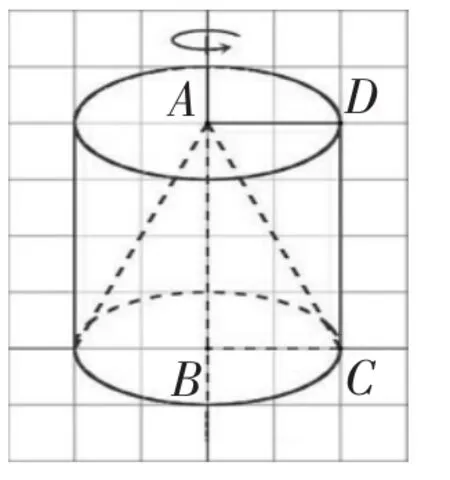
图2

师：能判断出此时的三角形ABC旋转后得到的圆锥与三角形ACD旋转后得到的空间相等吗？

生：我认为三角形ACD旋转后得到的空间大一些。

生：我认为它们是相等的。

有争议的课堂才有意思!乍一看，学生的判断似乎无懈可击，“穷则变，变则通，通则久”。

师：除了用对角线可以把长方形ABCD平均分成两份，还可以怎样平均分成两份？（取长或宽的中点均分。如图3、图4）

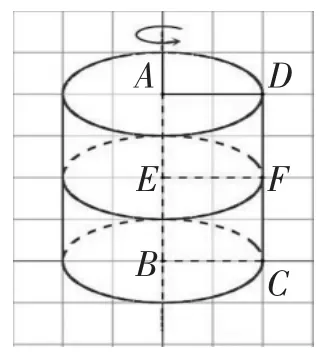
图3

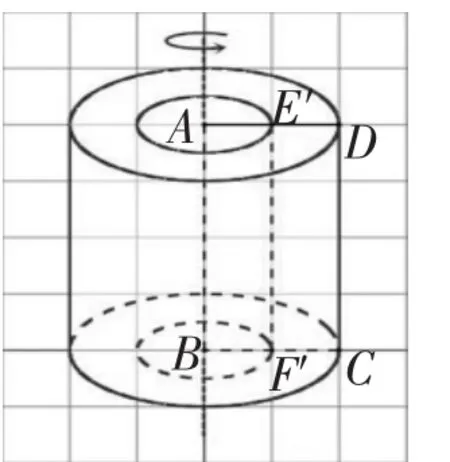
图4

师：照这位同学所说，长方形AEFD旋转后得到的圆柱和长方形EBCF旋转后得到的圆柱的体积相等。相等吗？

生：一眼就能看出来，体积都是8π。

师：同样，长方形AE′F′B旋转后得到的圆柱与长方形E′F′CD旋转后得到的空间的体积相等吗？

生：不相等，长方形AE′F′B旋转后得到的圆柱的体积是4π，而长方形E′F′CD旋转后得到的空间的体积是12π。

师：把长方形同样分成了2等份，分别绕轴旋转一周得到立体图形，它们的体积为什么有时相等，有时不相等呢？

生：图3的两部分离旋转轴的距离是相等的，而图4的两部分离旋转轴的距离是不相等的。体育节举行入场仪式，各班过弯道的时候，走在外道的同学的步伐要比走在内道的同学步伐大一些，旋转同样的角度，在外的长方形旋转后得到的空间大。

（作者单位：江苏南通市通州区西亭小学）

2017年第9期“讨论吧”话题：考场上学生不愿意检查试卷，怎么办？

期末考试时间为90分钟，有部分学生差不多60分钟就答完试题，然后就没事儿干了：有趴桌子上假装睡觉的，有玩儿尺子的，有扭动身子让凳子发出响声的……监考老师一再要求检查试卷，黑板上也用大字写着“认真检查”，可是学生仍然不愿意检查。

考试时学生不愿意检查试卷，怎么办？如果您遇到这种情况，将如何引导？

来稿（1000字左右）请发E-mail：changligang1@126.com。截稿日期：2017年6月20日。

（本话题由河南郑州市经济技术开发区朝凤路小学楚建娇老师提供，楚老师将获赠本刊2016年合订本一本）