遵循学路，建构概念的本质——“周长”教学实践与思考

◇刘善娜

遵循学路，建构概念的本质
——“周长”教学实践与思考

◇刘善娜

在教学“周长”这节课之前，我对学生进行了前测。结果发现，学生对“直线图形”比较敏感，即描画“直线图形”的“一周”的正确率明显高于描画曲线图形的“一周”的正确率；学生对“线段测量”具有经验化操作反应，也能借助测量工具（如所给的线）的暗示顺利测量曲线图形的周长。基于此，我对“周长”一课做了几点新尝试。

片段一：从离学生“最近”的图形出发，改“操场”为“长方形桌面”

从前测中发现，学生对“直线图形”，特别是对长方形、正方形“一周”的感知力远远高于曲线图形，因此，我决定从学生最有把握的长方形桌面切入。

师：（出示一个桌面）小胖蚁想每天跑步锻炼身体，它每天要绕这个桌面跑一圈。怎样跑才叫跑一圈呢？请用水彩笔描一下小胖蚁的跑步路线。

师：（展示学生作品，如图1）你赞同谁描的路线是桌面的一圈？

图1

生1：我认同1号作品。绕着桌面跑一圈就应该沿着桌面的边跑，2号都跑到桌面外面去了。

生2∶2号这样已经多跑了，比一圈多了。

师：怎样跑，正好是一圈？

生3：就是要沿着桌面的边跑。

（师板书：沿着边线）

生4：就是沿着这个长方形的4条边跑。

师：（课件演示，如图2）4条边，边线AB，边线 BC，边线CD，边线DA。

图2

师：你想让小胖蚁从哪里开始跑？谁来边指边说？

生：小胖蚁从点A开始跑，跑到点B，再跑到点C，跑到点D，最后回到点A。

（生边指边说，师动态演示）

师：刚才小胖蚁跑的时候，起点在哪里？沿着哪些边线跑？终点在哪里？

生：小胖蚁从点A开始跑,跑完边线AB跑边线BC，然后跑边线CD，最后跑边线DA，回到了点A。

师：（板书A→A）从点A出发，还可以怎样跑一圈？

生：还可以从点A出发，依次跑到点D、点C、点B，再回到点A。

师：两次跑，有什么共同点？

生：都是从点A出发回到点A，都是沿着长方形桌面的边线跑。

师：换个起点，会跑一圈吗？谁来？这一次起点在哪里？沿着边线跑到了哪个终点？

从学生最熟悉的长方形入手理解“一圈”，引出4条用字母命名的线段，助力其对周长概念本质的初步感知，并利用字母强化“起点”和“终点”的重合。

片段二：从学生已会的测线段开始，直击度量本质，体验线段长度累加

从前测中发现，学生会基于线段度量的经验主动测量图形中直边的长度。因此，我就从学生的这一经验出发，以长方形4条边线为素材直击周长的度量本质，让学生深度感悟周长是线段长度的累加。

师：那么，小胖蚁跑一周，跑了多长呢？

生：可以量一量啊。

师：从点A出发，怎么量？

生：先量出边AB，再量出BC、CD、DA。

师：这4条线段的长度，小胖蚁的爸爸已经测量出来了，依次是60cm、40cm、60cm、40cm。从点A出发，谁会算小胖蚁跑一周的长度？

生：60+40+60+40=200（cm）。

师：谁能说说式子中每个数的意思和算得的200厘米的意思？

（生答略）

图3

师：小胖蚁从点B出发跑一周的长度怎么算？

（生答略）

师：怎么都是200cm呀？

生：因为一周的长度就是这4条线段加起来的长度。

师：说得真好，这4条线段的长度加起来得到的200cm就是这个长方形桌面一周的长度。

基于学生会自发测量、累加线段长度的特点，将4条线段一段一段地从长方形桌面上移下来，将“一周的长度”直观地一段一段罗列，直击概念的度量本质，进一步感知“周长”是一周各边长度的累加。

片段三：把动态演示与静态描画相结合，感知“封闭”，深化“长度”

周长作为封闭图形一周的长度，是从静态边线的测量而得。如果把静态边线动态展开，使其脱离二维的面而被拉成一维的线段，就直观地放大了周长的一维长度测量的本质。在展开之后再将一维空间的线动态“合拢”，则能帮助学生更好地理解图形的“封闭”，也能在“展开”与“合拢”中渗透“化曲为直”和“守恒”的思想。

师：想象一下，如果把围成这一周的4条边线展开来，会是什么形状？

（生想象5秒后课件动态演示，如图4）

图4

生：哇，一条长长的线！

生：变成一条线段了。

师：这条线段，怎么这一头是点A,那一头也是点A啊？

生：因为点A是起点，也是终点。

生：因为是从点A这里打开的，闭合回去就还是点A。

师：好，那我们让它再闭合回去，（动态演示）发现什么？

生：点A和点A碰到一起了，变成一个点A了。

师：小朋友们，像这样能围起来的图形才有一周的长度，这样的图形就叫封闭图形。

前面的4条线段一段一段排列和这里的“展开”是有区别的，分段罗列后相加是突出各边长度累加，而封闭图形的“一周”被展开后是一条线，不仅凸显了周长的一维特性，而且渗透了“化曲为直”的策略，也有助于学生日后将周长与面积概念进行区分。

片段四：让学生明确自己的度量需求，从提供多种工具到放手让学生自己想办法测量

如果给学生提供卷尺、线，其实是给学生一种暗示：直尺不行了，用另外的工具试试？如果不给学生提供卷尺和线，学生就会自己开动脑筋，呈现“原始粗糙”的但非常有价值的测算方法。因此，将这个测算过程分为两段：先放手让学生测算5个图形或物品表面一周的长度，交流困难点和策略，初步感知“化曲为直”；再提供曲线测量工具让每个学生动手测算，进一步体验“化曲为直”。

师：请大家拿出1号信封，里面有1个瓶盖，1片树叶，1张周长测算记录表（如表1），要求同桌合作，测算出这5个图形的周长。时间：5分钟。开始！

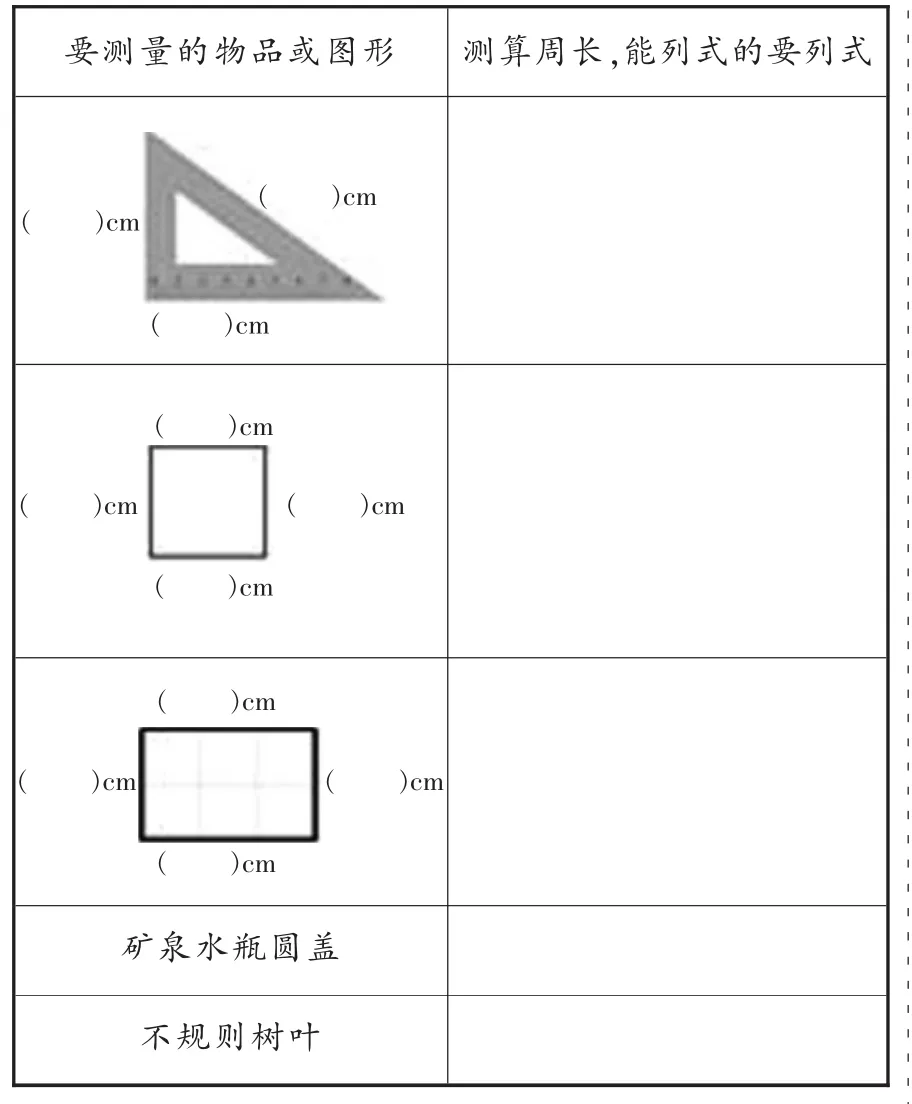
表1 周长测算记录表

生：老师，我们只有尺子，只测算出了3个图形的周长。

生：（齐）我们也是。

师：小组再商量商量，想想办法。

师：其实，数学家和小朋友们一样，也是先把这些直线图形的周长测量方法研究出来了，那我们就先交流一下这3个图形的周长测量过程。

（答案交流略。投影1份全部采用线段一一累加方式计算周长的表格，关注周长概念的理解，不关注公式化的方法）

师：那这些由曲线围成的图形，它们的周长怎么就不好测呢？

生：它们是曲曲弯弯的，尺子只能测量直直的。

师：曲曲弯弯的我们在数学上统称为“曲”的，直的尺子不方便测量曲的边。有没有同学能想出办法测量？（有三个学生举手）那就请这三位同学和大家分享一下自己的方法。

生1：我把直尺转动起来绕着瓶盖，一圈下来，就可以了。

生2：他动了，测不准。

师：他能想到把直的尺子转起来去测曲的边，很好，但操作难度比较大。

生3：我是想用剪刀把这个瓶盖展开来，像刚才的桌面一样打开，拉成平平的一条线，就可以测量了。

师：一起想象一下，这一圈展开会怎样？

生3：展开拉直成一条线就能测量了，可是，不好剪啊。

生4：我的办法是，把这片树叶对折、对折、再对折，再量出一段，数数有几段，就可以算出全部的长度了。

生5：我觉得这个办法可以，这样折啊，折啊，每一段就是直直的了。

师：折一折，也是想把曲的转变成直的，把曲边分割成很多段，每一段越小就越好测量。这个法子数学家求圆的周长时也用过呢。现在请你打开2号学具包（内有卷尺、毛线），想想用它们帮忙能否测量出较为准确的周长。

（汇报交流、小结略）

如果直接给学生测量的多种工具，学生能少走很多弯路。但是，这段追寻测算方法的路很有价值，不走这段路，学生就不会想出转动尺子、“展开”瓶盖、把软软的较对称的树叶对折再对折的方法。这些方法都直击周长概念的测量本质，学生等于像数学家一样走了一段曲线图形周长测算方法的寻求历程，感受了六年级求圆的周长中割圆术的思想萌芽，这种体验是非常必要的。遵循学路去认识“周长”，归根结底，学生的经验点、敏感点、兴趣点，是引导学生去建构概念本质的重要的路径导向点。

【本文系浙江省教育科研课题“小学数学相异构想调正策略的行动研究”（课题编号：02259）的阶段性研究成果之一】

（作者单位：浙江宁波市奉化区实验小学。作者系朱乐平名师工作室“一课研究”团队成员）