改进K均值模拟退火聚类算法的滚动轴承故障诊断*

姚立国，黄海松(贵州大学现代制造技术教育部重点实验室，贵阳550025)

改进K均值模拟退火聚类算法的滚动轴承故障诊断*

姚立国，黄海松
(贵州大学现代制造技术教育部重点实验室，贵阳550025)

为解决传统聚类分析方法K均值易求得最优局部解而非最优全局解的问题，引入一种新的中心点交换机制，提出将K均值与模拟退火法相结合的改进K均值模拟退火算法。该算法既继承了K均值可调整聚类中心的特点，又利用模拟退火法跳出最优局部解，能为故障诊断提供一种新思路。论文采用gr120数据首先验证了该算法的可靠性。然后基于该算法构建了滚动轴承振动故障诊断模型，接着采用美国凯斯西储大学轴承数据中心滚动轴承数据对算法及模型进行了应用验证，验证结果表明该方法能够诊断出滚动轴承的典型故障。

K均值;模拟退火;聚类分析;故障诊断

0 引言

随着中国制造2025的提出，制造行业迎来了新的机遇，越来越多的机械设备应用于各个行业。但机械故障的发生会影响生产效率，造成经济损失。因此，进行机械故障诊断显得尤为重要。聚类分析是重要的数据挖掘与模式识别方法，目的是寻找数据集中所包含的簇结构，根据数据属性，将数据集分群［1］，被广泛应用于故障诊断领域。

滚动轴承是机械设备的重要组成部分，其运行状态正常与否直接关系到整个机组的性能，因此对滚动轴承的振动信号进行故障特征提取和模式识别具有十分重要的意义［2］。启发式算法和K均值是两种不同的聚类分析方法。骆志高等［3］利用遗传算法的寻优功能，对故障的特征参数进行自动优化，最后利用逐次诊断理论，对变工况条件下的滚动轴承复合故障进行诊断。Muhammet Unal等［4］使用遗传算法对人工神经网络进行改进，用改进的方法对滚动轴承故障进行了验证实验测试。提供了一个最佳的熟练快速反应网络架构，可有效改进滚动轴承故障分类结果。郭艳平等［5］提出一种滚动轴承故障类型及故障程度识别方法，应用优化K均值聚类算法进行故障类型和故障程度分类。刘长良等［6］提出了基于变分模态分解和奇异值分解的特征提取方法，采用标准模糊C均值聚类进行故障识别，可精确、稳定提取故障特征。

聚类问题较为复杂，不同的算法也会影响聚类分析的求解效果。采用K均值算法求解，其易受到初始中心点的影响，不易找到全局最优解。而启发式算法求解易受数据聚类问题规模及数据复杂度的影响，模拟退火算法虽可跳出区域最优解，但在求解全局最优解时过于耗费时间，使得聚类结果不合乎预期的效果［7］。

根据滚动轴承故障诊断问题的要求，将K均值算法和模拟退火算法相结合，利用模拟退火算法求得全局最优解、K均值调整聚类中心位置的特点，解决了模拟退火法求解计算量大和K均值易落入局部最优解的缺点，明显提高聚类处理的效果。用美国凯斯西储大学轴承数据中心滚动轴承数据对该方法进行测试，并将其应用在滚动轴承振动故障诊断中，验证了该方法的有效性。

1 传统聚类分析算法

聚类分析是一个从杂乱的数据组中找出相同属性的数据，并进行聚类的NP难的复杂问题，也是数据挖掘、机器学习和模式分析的常用手段。为寻找正确的中心点，该问题被定义为一个性能函数的优化。给定聚类中心C，相应的数据点集X，Pref(X，C)定义了数据集和中心位置，如公式(1)。常用的评测分群好坏的性能函数是群内方差或均方误差［8］。通常用欧几里德距离公式(2)来计算数据点之间的距离。设xi，yj，zk为两个模式，有xi=(li1，li2，…，lim)T，yj=(lj1，…，ljm)T，zk=(，…)T。

K均值是数据聚类分析中常见的算法，其简单、实际操作容易、针对较大规模的数据也有很好的效率。其用数据到各聚类中心的距离来表示数据间的相似度，距离越小，相似度越高［9］。

模拟退火算法由Kirkpatrick等人在1983年提出，目的是处理组合优化的问题。此算法以低温凝固液体可得到稳定状态的结晶方式为背景，使用模拟训练方式来寻找合理且收敛的最优解［10］。模拟退火算法中的温度随时变化，因此，初始温度的设定及退火的调整即为模拟退火法中重要的一环。该算法的优点是可以跳出陷入局部最优解的循环;缺点是由于算法设计思路的局限，在求得全局最优解时计算量过大。

2 改进K均值模拟退火算法

为避免K均值算法和模拟退火算法在处理聚类时存在缺点，现有K均值模拟退火算法中心点交换不精确的缺点，提出了以SA为架构，利用SA的交换机制代替K-means的中心点交换的机制的改进K均值模拟退火算法，其衡量目标函数为群组的点与聚类中心点的最短距离总和。改进的K均值模拟退火算法，来降低出现局部最优解的概率，使数据聚类问题的处理中，所得数据聚类中组内距离总和最小［11-12］。算法流程图如图1所示。

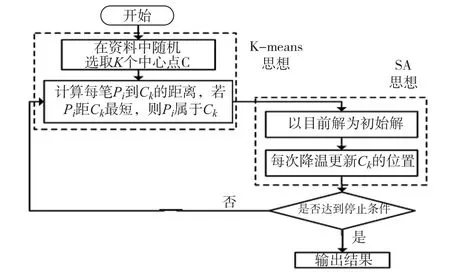
图1 改进K均值模拟退火算法流程图

利用模拟退火算法的交换机制代替K 均值中心点机制。SA的交换机制为:假设有K个群组，中心点为IDK，给定一个随机值，若是此值小于所设定的阈值，则将取的下一中心点为IDK减1;否则为IDK加1。

Step5:产生一个初始解，并以此解为目前状态;

Step6:设定该状态作为目前为止的最优解;

Step7:设定参数(T、α、m、n);

Step8:执行此步骤直到m和n结束;

Step9.1:若新目标值优于目前最优值，则将其取代;

Step9.2:若搜寻到的目标值差于目前最优值，则产生一个0到1之间的随机数。判断是否接受其较差目标值之排列方式;

Step1:从N个点的数据{X1，X2…XN}中，随机选取M个中心点{C1，C2…CK};

Step2:将数据分配到最接近的中心点，形成一个子集合;

Step3:计算群集中所有数据到中心的平均值，择优成为新的中心点;

Step4:重新计算并分配到各新的中心点C1*，…，形成新的群集，其中:

Step10:假如新的平均数值和先前的平均数值相同，则中止此程序，否则，使用新的平均数值当作群集的中心点，重复Step3～Step9.2直到收敛数值低于某个阈值时停止。

3 改进K均值模拟退火算法验证

进行数据处理和分析的参数设置:初始温度为100，降温次数为200，移动次数为50，降温系数为0.95，阈值为0.5。

TSP gr120［13］是旅行商问题常用的验证数据，为120个城市的经、纬坐标。这120个城市的分布比较随机，并无明显的聚类现象，是比较理想的聚类分析验证数据。而且，TSP gr120容易得到，可为以后的学者对聚类分析方法的研究提供比较便利。图2～图4为使用K均值模拟退火算法对TSP gr120数据进行聚类分析的结果示意图。

当分群数k=3时:

图2 TSP gr120分3群

当分群数k=4时:

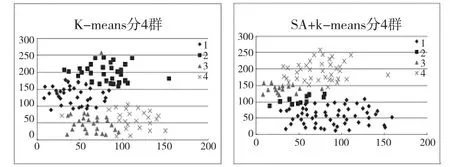
图3 TSP gr120分4群

当分群数k=5时:

图4 TSP gr120分5群

综合以上图中结果可以得知，改进K均值模拟退火算法的聚类分析效果均优于K均值模拟退火算法的效果，聚类分析效果在k=3之后有了明显的提升，在不同的聚类群数k(k=2～5)的情况下，两种算法的最短距离如表1所示。

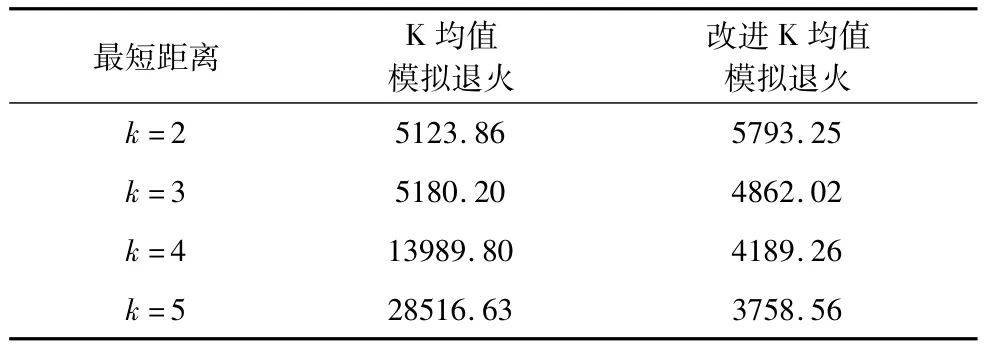
表1 改进K均值模拟退火与K均值模拟退火算法结果比较

4 改进K均值模拟退火算法的轴承振动故障诊断

4.1 振动故障诊断模型建立

滚动轴承是机械行业常用的装置，因其使用特点，其故障主要由振动产生。根据发生故障时的不同，状态分为三大类，包括外圈故障，内圈故障和滚动体故障等。用改进K均值模拟退火算法对已知故障进行聚类析，获得M个聚类中心{u1，u2，…，uM}。假设{X1，X2，…，XN}是一组待诊断的样本数据，则样本XN的故障类型由公式(5)求得。即根据待诊断样本数据与各已知聚类中心的欧几里德距离大小，将样本分配到离其最近的类别中。

得到训练样本聚类中心后，加入测试样本进行计算，更新聚类中心并完善诊断模型。在诊断过程中，该模型将不断添加新的测试样本，通过公式(5)和式(6)的不断迭代，使诊断模型进行不断地“学习”，从而调整聚类中心，不断完善诊断模型。

4.2 模型的应用验证

将提出的聚类诊断模型运用于工程实例。实验所用数据为美国凯斯西储大学轴承数据中心滚动轴承数据［14］，轴承为深沟球轴承，接触角90°，转速1750 r/min。将滚动轴承频谱特征中A(104.56Hz)、B (157.94Hz)、C(137.48Hz)3个频段作为故障频段，用训练样本完成诊断模型的学习，并用测试样本对诊断模型的有效性进行评估，进行外圈故障、内圈故障和滚动体故障诊断，所有样本都经过z分数归一化处理。表2和表3分别表示训练样本和测试样本。图5为不同轴承故障诊断聚类中心与样本数据的分布图，从图中可以看出该方法可将故障数据进行有效的聚类诊断。

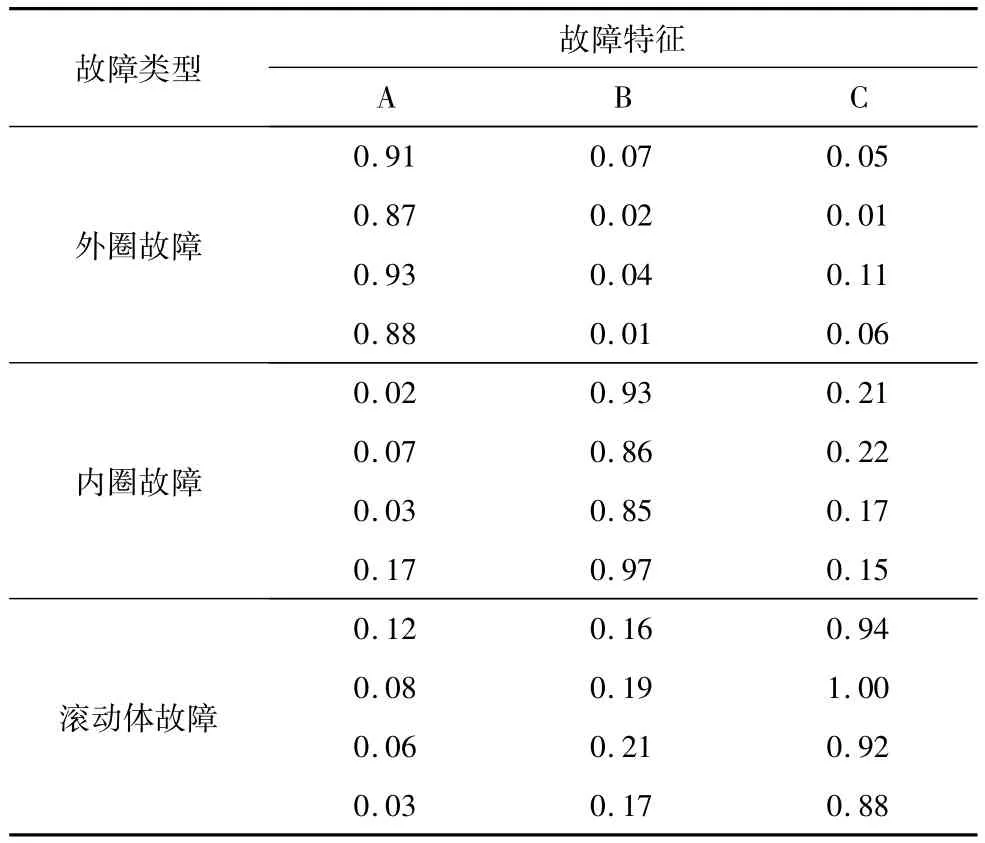
表2 振动频率训练样本

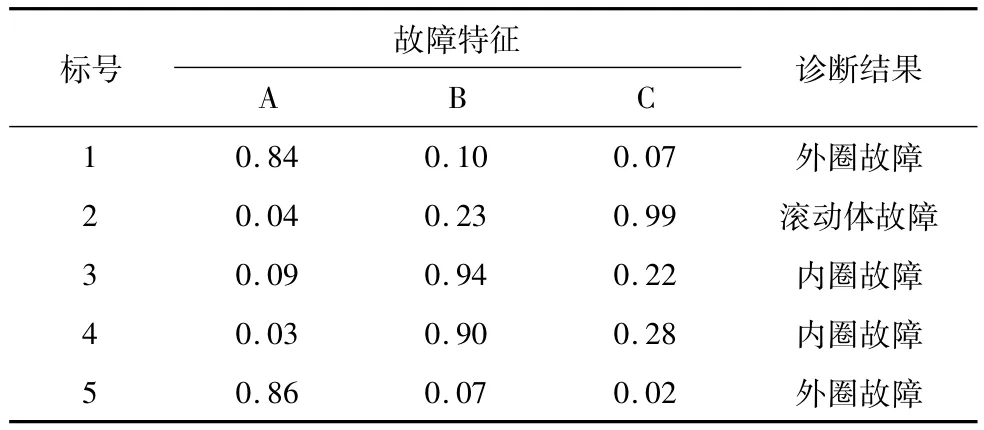
表3 振动频率测试样本

图5 不同轴承故障诊断聚类中心与样本数据

运用提出的改进K均值模拟退火算法对表2中的样本进行聚类训练，得到外圈故障的聚类中心为{0.8975，0.0350，0.0575};内圈故障的聚类中心为{0.0725，0.9025，0.1875};滚动体故障的聚类中心为{0.0725，0.1825，0.9350}。将表3中的样本进行聚类测试，得到样本1、2、3、4、5分别与外圈故障、滚动体故障、内圈故障、内圈故障、外圈故障聚类中心最近。将表2与表3中的样本数据归于一处，进行重新计算，得到外圈故障的聚类中心为{0.8658，0.0683，0.0492};内圈故障的聚类中心为{0.0642，0.9142，0.2292};滚动体故障的聚类中心为{0.0563，0.2063，0.9625}。如表4所示，通过对改进前后两种算法故障聚类中心的比较，发现改进后的算法得出的故障中心更优于原始算法得出的故障聚类中心。

表4 两种算法故障聚类中心比较

5 结论

在分析了K均值和模拟退火算法各自优缺点的基础上，以一种新的交换机制进行中心点的选取，提出了改进K均值模拟退火聚类方法的滚动轴承故障诊断模型。该方法利用K均值调整聚类中心位置和模拟退火法跳脱最优局部解的特性，来解决常规K均值落入局部最优解的情况。将该聚类方法与标准K均值模拟退火方法对gr120数据进行处理并比较，验证了该方法的有效性和优越性。基于该方法构建了滚动轴承振动故障诊断模型，通过美国凯斯西储大学轴承数据中心滚动轴承数据对模型进行应用验证，验证结果表明该模型能够诊断出滚动轴承的典型故障。

［1］王骏，王士同，邓赵红.聚类分析研究中的若干问题［J］.控制与决策，2012，27(3):321－328.

［2］张立国，李盼，李梅梅，等.基于ITD模糊熵和GG聚类的滚动轴承故障诊断［J］.仪器仪表学报，2014，35(11): 2624－2632.

［3］骆志高，陈保磊，庞朝利，等.基于遗传算法的滚动轴承复合故障诊断研究［J］.振动与冲击，2010，29(6):174－177，243.

［4］Unal M，Onat M，Demetgul M，et al.Fault diagnosis of rolling bearings using a genetic algorithm optimized neural network［J］.Measurement，2014，58:187－196.

［5］郭艳平，颜文俊.基于EMD和优化K－均值聚类算法诊断滚动轴承故障［J］.计算机应用研究，2012，29(7): 2555－2557.

［6］刘长良，武英杰，甄成刚.基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断［J］.中国电机工程学报，2015，35(13):3358－3365.

［7］Aghamohseni A，Ramezanian R.An efficient hybrid approach based on K-means and generalized fashion algorithms for cluster analysis［C］//Ai＆Robotics.IEEE，2015.

［8］Mekhmoukh A，Mokrani K.Improved Fuzzy C-Means based Particle Swarm Optimization(PSO)initialization and outlier rejection with level set methods for MR brain image segmentation［J］.Computer Methods＆Programs in Biomedicine，2015，122(2):266－281.

［9］KarS，Sharma K D，Maitra M.Gene selection from microarray gene expression data for classification of cancer subgroups employing PSO and adaptive K-nearest neighborhood technique［J］.Expert Systems with Applications，2015，42 (1):612－627.

［10］Karasulu B.An approach based on simulated annealing to optimize the performance of extraction of the flower region using mean-shift segmentation［J］.Applied Soft Computing，2013，13(12):4763－4785.

［11］Karami A，Guerrero-Zapata M.A fuzzy anomaly detection system based on hybrid PSO-Kmeans algorithm in contentcentric networks［J］.Neurocomputing，2015，149:1253－1269.

［12］Li H，He H，Wen Y.Dynamic particle swarm optimization and K-means clustering algorithm for image segmentation［J］.Optik-International Journal for Light and Electron Optics，2015，126(24):4817－4822.

［13］TSPLIB/OsmSharp.TSPLIB.Benchmark/Problems/TSP/ gr120.tsp(2015-4-20)［EB/OL］.https://github.com/ OsmSharp/TSPLIB/blob/master/OsmSharp.TSPLIB.Benchmark/Problems/TSP/gr120.tsp

［14］The case western reverse university bearing data center website［EB/OL］.http://www.eecs.edu/laboratory/ bearing，2013－05－012.

(编辑李秀敏)

Rolling Bearing Fault Diagnosis Based on Improved K－means Simulated Annealing Clustering Algorithm

YAO Li-guo，HUANG Hai-song
(Key Laboratory of Advanced Manufacturing Technology，Ministry of Education，Guizhou University，Guiyang 550025，China)

In order to solve the traditional clustering analysis K-means algorithm easy to obtain the optimal local solutions rather than the global optimal solution of the problem，introduced a new center exchange mechanism，an improved K-means simulated annealing algorithm is proposed，w hich combines the value of K-means w ith the simulated annealing method.This algorithm not only inherits the characteristics of the K-means to adjust the cluster center，but also can provide a new w ay of thinking for the fault diagnosis by using the simulated annealing method to jump out the optimal local solution.Gr120 data is used to verify the reliability of the algorithm.Then the algorithm for constructing the rolling bearing vibration fault diagnosis model based on.And then，the United States at Case Western Reserve University bearing data center rolling bearing data the algorithm and modelare verified，verification results show thatthe method can diagnose the typical faults of rolling bearing.

K-means;simulated annealing;cluster analysis;fault diagnosis

TH133.3;TG506

A

1001－2265(2017)04－0114－04

10.13462/j.cnki.mmtamt.2017.04.029

2016－06－16

贵州省重大基础研究项目(黔科合JZ字［2014］2001);贵州省自然科学基金项目(黔科合J字［2015］2043号);贵州省高端装备产业技术军民融合协同创新中心建设项目(黔教合协同创新字［2015］02);贵州省工业攻关计划项目(黔科合GZ字［2015］3034号);贵州省机场集团有限公司贵州省机场系统智能化控制技术应用工程研究中心建设项目;贵州省科技计划项目(黔科合支撑［2016］2327号);铜仁市农业科技攻关项目(铜市科研［2016］17号－8);贵州大学研究生创新基金(研理工2016025)

姚立国(1990—)，男，甘肃永昌人，贵州大学硕士研究生，研究方向为制造物联与制造大数据，(E－mail)yaoliguo1990@163.com;通讯作者:黄海松(1977—)，女，彝族，贵州大方人，贵州大学教授，博士生导师，研究方向为制造物联与制造大数据，(E－mail)huang_h _s@126.com。