一种时间最优关节柔顺的码垛机器人运动规划*

陈晓炬，李辉，吴献钢(电子科技大学.航空航天学院;.机械电子工程学院，成都611731)

一种时间最优关节柔顺的码垛机器人运动规划*

陈晓炬a，李辉a，吴献钢b
(电子科技大学a.航空航天学院;b.机械电子工程学院，成都611731)

针对码垛机器人传统时间最优规划中存在的关节脉动较大、轴间等待等问题，提出了一种基于时间最优关节柔顺的二次轨迹规划方法。以传统规划为预规划，若预规划存在轴间等待，则进行第二步规划:采用三次样条曲线，将预规划所得的S曲线改造成非对称S型曲线;同时，采用线性插值法，根据轴间等待时长实时调整相应关节的加加速度值，直到关节间等待不再发生，从而实现柔顺控制。经实验验证，在不损失工作效率的情况下，该方法可有效降低关节脉动。

码垛机器人;轨迹规划;非对称S曲线;关节柔顺控制

0 引言

码垛机器人是一种广泛运用于物流搬运行业的工业机器人。为了完成给定的码垛任务，机器人必须按照一定的轨迹进行运动，而轨迹规划是机器人码垛效率和运行性能的基础。

轨迹规划多采用高次样条曲线、B样条曲线等插值理论，通常以时间最优、能耗最优、脉动最优中的一个或多个为优化目标［1-8］，运用遗传算法(GA)［3］、粒子群算法(PSO)［4］、序列二次规划(SQP)［5］等智能方法进行规划。曹波等采用提升直线运动的最高点，提出了针对串联型搬运机器人的时间最优规划［1］，但未考虑关节可能处于等待且可柔和化的问题。王会方等采用7次B样条曲线插值，提高了轨迹平滑性，能降低关节冲击［6］，但计算量较大。王学琨等采用分段3-5-3多项式曲线进行插值［7］，降低了一些运算量。Sarmad Riazi等针对能耗最优，提出机械臂在长臂展状态时可用缓慢移动来代替静止等待，以降低能耗［8］，但增加了控制的复杂性。Yongqiang Xiao等以时间-脉动最优为目标，以多项式样条曲线进行轨迹插补，采用黄金法则求得最优轨迹［9］，但方法相对繁琐，运算量较大。

实际工程中，智能算法和高次样条曲线计算量较大，不利于机器人实时加减速控制。本文在文献［1］提出的时间最优规划基础上，进一步探索关节脉动柔和化方法，采用三次非对称S曲线(AS，asymmetric S-curve)进行规划，提出一种时间最优关节柔顺的二次规划方法。

1 传统规划中轴间等待问题的描述

本文采用的关节型码垛机器人是一种四自由度工业机器人，由腰部旋转A轴、大臂B轴、小臂C轴和手抓旋转D轴等4个关节组成，其中B、C两轴的减速比、电机和驱动器相同。在笛卡尔坐标系下，由B、C两轴合成插补实现水平进退和竖直升降运动。实际控制中，需通过运动学逆解公式［10］，将(X，Y，Z)坐标转换为关节坐标(θ1，θ2，θ3，θ4)。

传统规划中，以时间最优为目标，以S型曲线为基础进行轨迹插补规划［1］，各关节i在最大允许参数(最大允许速度Vimax、最大允许加速度aimax、最大允许加加速度Jimax，i=1，2，3，4)下，实现从抓取点P0(X0，Y0，Z0)到放置点P3(X3，Y3，Z3)的PTP运动，同时为了确保安全，需经过中间点P1(X1，Y1，Z1)和P2(X2，Y2，Z2)，其中四个点坐标均已知。工作过程依次为直线上升阶段P0→P1、到位阶段P1→P2、直线下降阶段P2→P3，其运行时长分别为T1，T2，T3，如图1所示;其中P0→P1和P2→P3阶段由B、C轴合成插补完成笛卡尔空间直线运动，A、D轴静止;而在P1→P2阶段，四个轴同时运动。

图1 笛卡尔空间下的码垛运动轨迹

为了提高工作效率，应尽量使单次总运行时间T=T1+T2+T3最短。实际工程中，如图2所示，当抓取点和放置点距离较远，即A轴目标旋转距离较大时，将发生轴间等待现象:B、C轴合成插补上升到最高点Zmax后需等待一段时间Tw，使A轴旋转到位后才能开始下降，否则将与托盘上已码包垛发生碰撞。

图2 发生轴间等待时的速度曲线

同时，由于各关节均采用最大允许运动参数，尤其是最大加加速度Jimax，将带来较大关节脉动，长期有损机器人机械和减速器、电机、驱动器等零部件寿命。其中，关节i在单次运行时间T下的脉动Si由如下公式决定:

因此，可以考虑在不影响传统规划总时间最优的情况下，充分利用等待时间，对处于等待的关节进行柔顺控制，降低其加加速度值Ji，从而降低关节脉动。

2 非对称S曲线加减速控制模型

图3为典型七段AS曲线的位移、速度、加速度、加加速度曲线，根据不同加速度依次分为:加加速段、匀加速段、减加速段、匀速段、加减速段、匀减速段和减减速段，其方程见文献［11］。

工程实践发现，当轴间等待情况发生时，为了使直线运行时间T1+T3最短，从而使总时间T最短，传统S曲线规划会充分发挥各关节的加速性能，以尽可能大的速度经过P1或P3点，使得P1或P3点的瞬时速度为当前S曲线中的最大速度Vim。因而，可将传统规划作为预规划，以Vim为分界点，沿用当前S曲线的加速阶段和匀速运行阶段，并针对减速阶段采用更小的关节i加加速度值(其他运动参数可沿用最大值)，进行曲线二次规划，改造成非对称S曲线，其中i=1，2，3，4。根据不同曲线类型进行改造，具体如下:

图3 典型七段AS曲线模型

(1)如图4所示，当位移足够长时，曲线可以加速到关节最大允许速度Vimax，为七段AS型加减速曲线。其前4个阶段沿用预规划时七段S曲线的前4段，则方程同于S曲线的前4段，具体见文献［1］;根据前4段的方程，可求得第4阶段末端时刻t4的最大速度值Vim和前4段位移总和Si14:

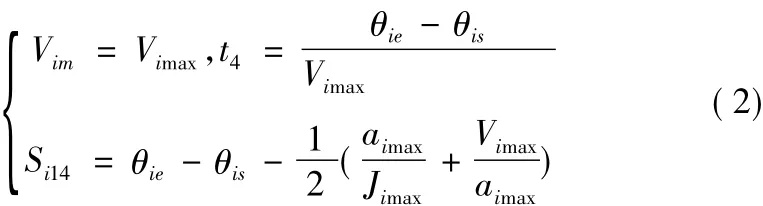
其中，θis为规划起始位置值，θie为预规划所得的终点位置值，Vim为当前规划中最大速度值，Vimax为关节最大允许速度(由电机最高转速和关节减速比决定)，aimax为最大允许加速度(由电机速度-转矩特性和关节承受的最大转动惯量决定)，Jimax为最大允许加加速度(由实验测得)。

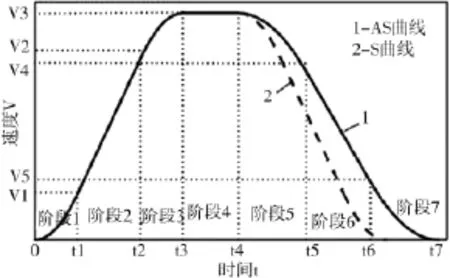
图4 长位移七段AS速度曲线

根据公式(2)，令θi(t)为关节i的转角，其后3段插补方程应满足以下约束条件:

本文选用三次样条曲线规划，可求得后3段速度曲线方程为:

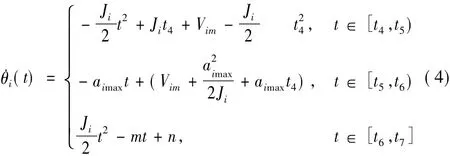
其中，Ji为二次规划后的加加速度值，v3=Vim=Vimax

(2)如图5所示，若目标位移较小不足使关节加速到Vimax，则曲线退化为6段，第4阶段消失且第2、6阶段匀加速过程缩短，称为中位移六段AS曲线。此时，沿用六段S曲线的前3个阶段，方程同见文献［1］;其后3段边界条件同于公式(3)，因此其5、6、7阶段的轨迹方程分别与七段AS曲线的5、6、7阶段相似，见公式(4)，其中不同的是v3=Vim≤Vimax。

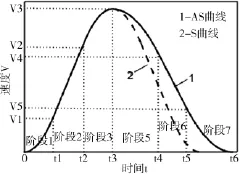
图5 中位移六段AS速度曲线

(3)如图6所示，当目标位移更小，关节无法达到最大加速度aimax，匀加速段消失，曲线将退化成4段，称为短位移四段AS曲线。此时，沿用四段S曲线的前2个阶段，方程同见文献［1］;其阶段5起始边界条件与七段AS曲线阶段5相同，则方程也相同，其中Vim=v2;阶段7的起始边界条件由阶段5末端点决定。因此，需求出阶段5末端点的参数。

图6 短位移四段AS速度曲线

根据加减速段和减减速段的对称性，有:

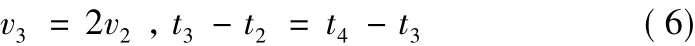
根据阶段5的方程和公式(6)可求得:

因此，可得其阶段7的速度方程为:

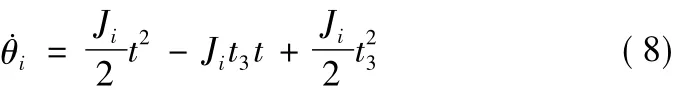
3 柔性AS曲线二次规划方法

3.1 加加速度柔和化

根据公式(1)，关节加加速度Ji体现关节的脉动程度，其取值越大则脉动越大;若取值过小则加减速时间过长。为此，针对传统规划中关节脉动较大的问题，提出一种关节柔顺策略:将发生等待的关节作为优化对象，根据不同的轴间等待时长τ实时调整其加加速度值Ji，以此作为AS曲线二次规划的基础。柔性体现在随着码垛过程垛、层、包的位置变化，其Ji值可变，亦即关节脉动可变。其工程意义是，在不影响总运行时间最短的前提下，轴间等待时间越长，关节可柔和程度越大。

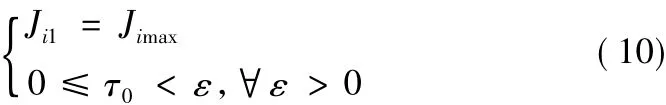
其Ji=f(τ)的关系如图7所示，若τ较长，此时设置较小的Ji;若τ较短，取较大的Ji;若无轴存在等待，为了不损失码垛效率，不进行加加速度柔和化，即无需进行二次规划。

其中，Ji0、τ1可在二次规划时，根据不同目标位移和码垛对象类型设置不同的值。通常取

图7 Ji=f(τ)关系图

3.2 AS曲线二次规划算法

在进行目标关节柔顺二次规划时，AS曲线的Ji小于Jimax而其余运动参数不变，在机器人允许最大上升高度Ztop之内，将使机器人在上升到最高点Zmax后仍继续往上运动，到达新的最高点Z'max处，如上图1所示。本文的柔性AS加减速控制采用PTP运动模式，具有以下4个约束条件:

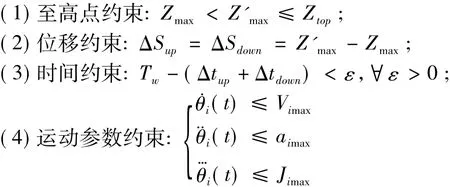
其中，ΔSup为二次规划后增加的直线上升位移，ΔSdown为二次规划后增加的直线下降位移，Tw为轴间等待时长。

基于公式(9)的加加速度理论，可得柔性AS曲线轨迹规划流程如图8所示。

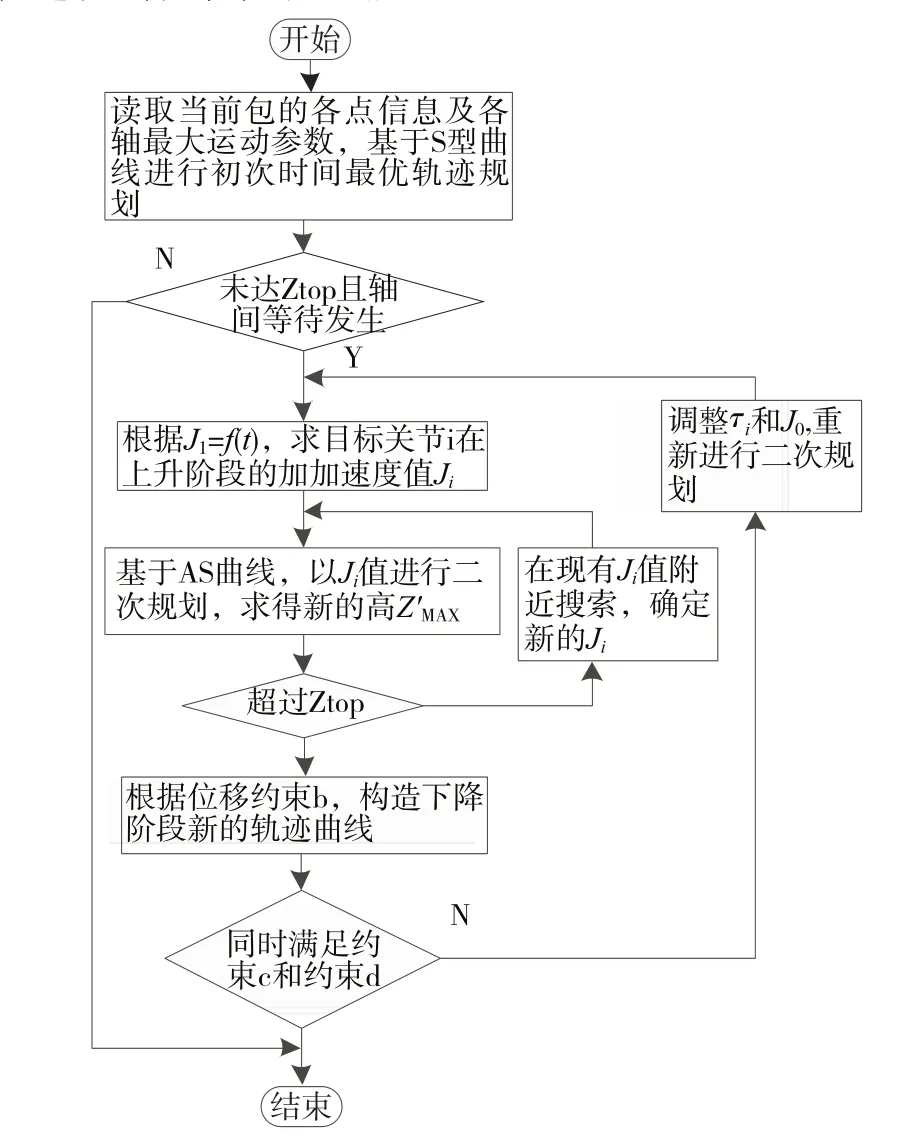
图8 柔性AS曲线二次规划算法流程图

二次规划算法的关键是，如何确定合适的加加速度Ji和新至高点Z'max。而Ji与Z'max紧密相关，若Ji过大，则Z'max过低，仍有等待发生，关节柔顺优化不完全;若Ji过小，使得Z'max过高，则直线运动时间T1+T3过长，破坏原有的时间最优。通常情况下，需在公式(9)所得值附近进行新的Ji值寻优搜索，才能充分利用等待时间，实现最大限度的关节柔和优化。

4 实验结果与分析

采用实物码垛作业验证该二次规划方法的正确性，如图9为成都某机器人公司的码垛机器人工程样机实验平台。实验条件:负载包(不含手抓)45kg，抓取点P0(2145，0，1360)，放置点P3(－260，1500，780)，直线上升高度280mm，下降高度180mm。机器人运动参数约束如表1所示。

目前，对木兰溪进行治理时，逐渐由原来的下游流域治理转向全流域全面治理，水利部门在此基础上，抓住发展机遇，转变了对木兰溪的治理以及发展观念，从而全面建设木兰溪的防洪工程，对木兰溪的干流进行全线治理，进而有效提高木兰溪的沿线安全，使防洪安全以及水环境治理和景观建设有效结合，为创建优美莆田城市、建设木兰溪百里风光带奠定良好的基础。

表1 运动参数约束

图9 码垛机器人实验平台

以上测试条件下，传统规划中B、C合成插补轴存在等待，等待时长为Tw=0.29s。因此，取i=2，3和Ji0=20(°/s3)，Ji1=60(°/s3)，τ1=0.8s，τ0= 0.01s进行二次规划，代入公式(9)可解得Ji= 45.82(°/s3)，经过寻优搜索后，最终确立Ji= 46.76(°/s3)。

图10为二次规划后得到的速度优化轨迹图，与传统规划的结果(图2)相比，可以看出:二次规划后，轴间等待消失，B、C合成插补曲线实现无缝衔接，关节变得更加柔顺;同时，优化前后的运行时间相同，均为最短T=4.212s，保证了工作效率。

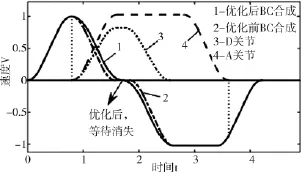
图10 二次规划后的速度曲线

5 结束语

本文分析了在传统时间最优规划上存在的轴间等待现象，阐述了关节柔顺的必要性，并将预规划的S曲线改造为非对称S曲线，同时采用线性插值理论，提出一种随轴间等待时长变化而变化的加加速度可柔和化策略，从而在保证工作效率前提下，实现了关节柔顺控制。经实验验证，二次轨迹优化后，关节脉动降低，可提高机器人寿命。另外，在AS曲线二次规划算法中，还可考虑运用更高效、直接的搜索方式定位加加速度值，在以后工作中，可作进一步研究。

［1］曹波，曹其新，童上高，等.基于时间最优的搬运机器人运动规划［J］.组合机床与自动化加工技术，2012(7): 33－38.

［2］张云峰，马振书，孙华刚，等.一种基于混合策略的排爆机器人目标抓取轨迹规划［J］.机床与液压，2015，43(21): 86－90.

［3］R Saravanan，S Ramabalan，C Balamurugan，et al.Evolutionary Trajectory Planning for an Industrial Robot［J］.International Journal of Automation＆Computing，2010，7(2): 190－198.

［4］李小为，胡立坤，王琥.速度约束下PSO的六自由度机械臂时间最优轨迹规划［J］.智能系统学报，2015，10(3): 393－398.

［5］A Gasparetto，V Zanotto.A New Method for Smooth Trajectory Planning of Robot Manipulators［J］.Mechanism and Machine Theory，2007，42(4):455－471.

［6］王会方，朱世强，吴文祥.基于INSGA-II算法的机械手多目标轨迹规划［J］.浙江大学学报:工学版，2012，46(4): 622－628.

［7］王学琨，李刚，周东凯，等.基于DE的时间最优6-DOF机械臂轨迹规划算法［J］.计算机仿真学报，2015，32(8): 332－337.

［8］Sarmad Riazi，Kristofer B，Oskar W，et al.Energy Optimization of Multi-robot Systems，in Automation Science and Engineering(CASE)［J］.2015 IEEE International Conference on，2015，8(4):1345－1350.

［9］Yongqiang Xiao，Zhijiang Du，Wei Dong.Smooth and Near Time-optimal Trajectory Planning of Industrial Robots for Online Applications［J］.The Industrial Robot，2012:169－172.

［10］张志强，臧冀原，贠超.混联码垛机器人运动学分析及仿真［J］.机械设计，2010，27(11):47－51.

［11］潘海鸿，杨微，陈琳，等.全程S曲线加减速控制的自适应分段NURBS曲线插补算法［J］.中国机械工程，2010，21(2):190－195.

(编辑李秀敏)

Time-optimal and Joints-compliant Motion Planning for Palletizing Robot

CHEN Xiao-jua，LI Huia，WU Xian-gangb
(a.School of Aeronautics and Astronautics;b.School of Mechatronics Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China)

In order to decrease the pause among joints and reduce severe pulsation in Palletizing Robot running in the w ay of traditional time optimal planning，a new new-step planning method with time-optimal and joints compliance control w as proposed.When the pause occured，the process should move on to nextstep: the symmetric S-curve obtained after traditional planning should be modified into asymmetric S-curve through a cubic spline.And based on Linear Interpolation，the joint’s jerk w ould be set diversely w ith different w aiting duration until the pause didn’t occur any more so that the trajectory became more compliant.The experiment showed that，this method can effectively reduce the pulsation and ensure the productivity.Key words:palletizing robot;trajectory planning;asymmetric S-curve;joints compliance control

TH165;TG659

A

1001－2265(2017)04－0018－04

10.13462/j.cnki.mmtamt.2017.04.005

2016－07－28;

2016－09－04

四川省科技支撑计划项目(2015GZ0021、2016GZ0168)

陈晓炬(1991—)，男，福建龙岩人，电子科技大学硕士研究生，研究方向为机器人运动控制，(E－mail)kevin_cxj@126.com。