高频破碎器齿轮接触应力分析及齿廓修形*

刘文，蔡家斌，丁成波，王兴旺(贵州大学机械工程学院，贵阳550025)

高频破碎器齿轮接触应力分析及齿廓修形*

刘文，蔡家斌，丁成波，王兴旺
(贵州大学机械工程学院，贵阳550025)

高频破碎器的激振力由斜齿轮上的偏心块产生，斜齿轮的失效会导致高频破碎器无法正常工作。利用Solidworks精确建立某型高频破碎器的斜齿轮三维模型，将其导入ADAMS中进行动力学分析，确定其接触参数，求解出齿轮的扭矩和啮合力，然后将得到的参数作为有限元分析的边界条件，在ANSYS workbench中进行齿面接触应力分析，发现斜齿轮啮合时出现了应力集中现象，最后对斜齿轮齿顶进行齿廓修形。结果表明，修形后的最大齿轮接触应力降低了30.4%，对高频破碎器齿轮设计具有指导意义。

高频破碎器;斜齿轮;动力学分析;有限元分析;齿廓修形

0 引言

高频破碎器是一种新型的矿山破碎设备，其利用液压马达将挖掘机的液压能转化为机械能，从而驱动偏心块使之产生破碎岩石的破碎力，主要用于矿山的岩石破碎以及公路改造中［1］。高频破碎器的偏心块与斜齿轮紧固在一起，如图1所示。当两个斜齿轮相互啮合转动的时候，就会产生正弦函数的激振力，从而驱动高频破碎器的振动箱体破碎岩石，斜齿轮的失效将会导致偏心块无法正常工作，从而影响高频破碎器的使用寿命。刘涛等［2］运用ADAMS对高频破碎器振动箱体作运动学分析，得出初始阶段齿轮间啮合力较大，对齿轮要求很高，但没有对此进一步分析，而何文强等［3］通过对高频破碎器静力分析，得出从动齿轮的最大接触应力超过材料的屈服极限，存在安全隐患，但没有给出齿轮具体的失效形式和解决办法。由于高频破碎器斜齿轮啮合时不仅受到液压马达的扭矩产生的啮合力，还受到偏心块产生的偏心力和岩石传递的反作用力的影响，受力复杂，难以以理论计算来确定齿轮具体受力的大小。

随着计算力学和计算机仿真技术的发展，很多软件能够运用于解决实际问题并能够得到与理论公式近似甚至更精确的计算结果［4］。因此文章首先运用Solidworks软件精确生成高频破碎器实际的主齿轮与从齿轮模型，然后导入ADAMS中进行动力学仿真，得到齿轮啮合时产生接触力以及马达转矩，分析其受力历程;然后将计算出来的力矩与接触力参数作为ANSYS workbench的边界条件，运用静力学模块得到齿轮在正常工况下的接触应力图，通过与赫兹公式比较，验证其结果的正确性，之后对斜齿轮齿顶进行齿廓修形，解决轮齿应力集中问题。研究高频破碎器斜齿轮啮合时齿面的接触应力以及解决齿轮应力集中的方法对于预防齿轮失效和提高高频破碎器的使用寿命具有重要的意义，同时也为新高频破碎器的斜齿轮设计提供参考。

图1 齿轮偏心块

1 斜齿轮传动动力学分析

1.1 模型的建立

齿轮模型的准确性直接影响着动力学分析和有限元分析的结果，利用Solidwirks精确建立标准渐开线斜齿轮的三维模型，并在此基础上建立精确的偏心块三维模型，将其转换成PARASOLID格式的文件，然后导入ADAMS软件，为了显示效果更好，将主动齿轮渲染为红色，从动齿轮渲染为绿色，如图2所示，斜齿轮相关参数如表1所示。

图2 齿轮偏心块三维模型

1.2 碰撞参数选取

1.2.1 碰撞参数的选取

碰撞是一种复杂的非线性问题，在ADAMS中碰撞仿真涉及到很多参数的定义，如果参数设置不正确，就会影响仿真的准确性，甚至会导致仿真失败。ADAMS中有两种定义碰撞力的方法，一种是补偿法(RESTITUTION)，另一种是冲击函数法(IMPACT)，前者的参数很难设置，本文选择冲击函数法，根据文献［5］，对于金属之间的碰撞，选择碰撞指数为1.5，最大阻尼系数为10，切入深度为0.1mm。对于旋转的物体，其刚度系数K由接触物体的结构形状和材料决定［6］:

式(1)～式(3)中，R为两齿轮接触点的综合曲率半径;Rn1、Rn2分别为主齿轮、从齿轮的曲率半径，d1主齿轮的分度圆直径;u为两齿轮的传动比;αt为端面压力角，α=arcta;β为基圆螺旋角，

tbβb=arctan(tanβcosαt);E1，E2为两齿轮材料的弹性模量，μ1，μ2为材料泊松比。

表1 斜齿轮相关参数

主动齿轮与从动齿轮的材料均一样，为合金结构钢20CrMnTi，采用渗碳淬火回火的热处理方式，材料的弯曲疲劳极限为σFE=850MPa，材料的接触疲劳极限为σHlim=1500MPa，材料的弹性模量E1=E2= 2.07×105MPa，泊松比μ1=μ2=0.27，根据表1的相关参数以及上述公式，计算得出K=4.3×105N/mm由于齿轮偏心块是浸泡在密闭的润滑油腔内，润滑条件非常好，所以选取动摩擦系数为0.05，动摩擦系数为0.08。

1.2.2 求解器及仿真步数的设置

为了使运算结果更加精确，选择ADAMS里计算效率高的GSTIFF积分器以及SI2的积分格式，SI2格式可以避免JACOBIAN矩阵的病态，并且考虑了约束方程，求解精度较高［5］。主齿轮的额定转速为1000r/min，为避免开始仿真时转速突变引起冲击，这里使用阶跃函数，使主齿轮在0.2s内平缓提速到额定转速，即:STEP(time，0，0d，0.2，6000d)，仿真设置为1s，步长为5×10－4s。

1.3 仿真结果

通过一段时间的仿真计算，得到液压马达的力矩图以及斜齿轮齿面接触力图，如图3、图4所示。

图3 液压马达力矩

图4 斜齿轮啮合接触力

从图3力矩图来看，初始的一瞬间，会有一个较大的启动转矩，在之后的0～0.2s的时间段内，力矩会随着加速度的变化而变化，呈现二次函数样式，最大值约3250N·m，这和STEP函数加速度曲线是相吻合的。由液压马达输出转矩公式T=以及功率公式P=(式中，V为液压马达排量，ΔP为压差，g为机械液压效率，n为马达转速)来看，当挖掘机输出的功率一定时，液压马达输出转矩与转速是成反比例关系的，当负载转矩超出液压马达的最大转矩时，液压马达会通过减小流量来降低转速来适应超载工况，因此在0～0.2s加速阶段，力矩图并不能反映液压马达真实的工作状况，可以将其忽略，不纳入之后的分析计算之中。

在0.2s之后的稳定期内，力矩会随着时间的变化出现一个周期性循环，周期为0.06s，即齿轮转动一圈的时间。在一个周期内，力矩从大到小，再从小到大，这是由于偏心块重心随着齿轮转动而变化的缘故。从图3可以看出，平衡期内，最大转矩约为2000N·m，平均转矩为1100N·m，这和设计之初所选的液压马达在极限压差下转矩为2078N·m是相吻合的，从侧面证实了仿真数据的正确性。

从图4可以看出，斜齿轮啮合时的接触力0～0.2s内也有一个不稳定的过程，在0.2s之后，接触力随着力矩的变化而变化，具有周期性。在平衡期内，最大接触力约为32054N，平均接触力约为24kN，最大和最小接触力在平衡线上下波动，这是由于齿轮在传动过程中伴随着振动和冲击现象造成的。

由于偏心块产生了偏心力，然后作用在斜齿轮上，使得斜齿轮轮齿之间的实际最大接触力远比理论计算的最大啮合力F==10864N大，因此，当n将力矩作为有限元分析边界条件的时候，需要将实际接触力转化为等效力矩:T==5904 N·m，而不是将2000N·m作为有限元分析的边界条件。

2 斜齿轮齿面接触应力有限元分析

2.1 模型建立及网格划分

在建立有限元模型的时候，为了节约计算机计算时间，提高收敛可能，将啮合的齿轮简化为只有五个齿的斜齿轮啮合［7］，并将其导入ANSYS Workbench的静力学模块中，划分网格，并对齿轮啮合的齿面进行细化网格，提高有限元分析精度，如图5所示。最终网格模型的节点为497612个，单元为114099个，单元质量的平均值为0.92(1最好)，雅克比平均值为1.24(1最好)。

图5 斜齿轮网格划分模型

2.2 接触设置及边界条件施加

斜齿轮轮齿啮合时的接触是一个非常复杂的非线性问题，在ANSYS WORKBENCH软件中，主要接触算法有罚函数法(Pure Penalty)、拉格朗日乘子法(Normal Lagrange)和增广拉格朗日乘子法(Augmented Lagrange)，罚函数法由于需要人为加入罚因子，过小不起作用，过大会引起方程的病态，而拉格朗日乘子法会由于乘子的引入使得系统的求解规模增加，并且必须采取适当的方法抑制矩阵中出现零主元，增广拉格朗日法将前两者联合使用，既吸收了罚函数法和拉格朗日乘子法的优点，又不增加系统的求解规模，收敛速度比较快［8］，因此本文采用增广拉格朗日法来求解;接触刚度影响了接触面之间的渗透量，过大会引起收敛困难，过小会导致渗透量太大，模拟效果不准确，根据文献［9］，定义接触刚度为1，允许最大渗透量为0.1mm，由于斜齿轮浸泡在润滑油里，润滑良好，设置动摩擦因素为0.08，静摩擦因素为0.05;最后，在ANSYS Workbench材料库里新加材料，设置为20CrMnTi。

在液压马达输出最大扭矩的瞬间，假定从齿轮固定，主齿轮施加等效力矩，因此在ANSYS Workbench静模块中，在从齿轮的内径处施加固定约束，限制其各方向的自由度;对主齿轮施加圆柱约束，限定其轴向、径向运动，并在主齿轮内径表面施加力矩载荷，即为上文所求的等效力矩载荷，大小为5904N·m。

2.3 有限元结果

当软件求解处理完成后，在SOLUTION后处理栏目中添加等效应力和安全因子工具，等效应力遵循材料力学第四强度理论，当其值达到材料的屈服强度之后，就认为此点发生了屈服;安全因子用于直观的查看材料的屈服情况，当其值小于1的时候，就认为材料处于塑性变形的危险状态。主从齿轮的应力云图与安全因子云图如图6～图8所示。

图6 主齿轮接触应力云图

图7 从齿轮接触应力云图

图8 齿轮安全因子云图

从图6和图7云图可以看出，斜齿轮啮合的接触区域分布在三个参与啮合的轮齿上，中间的轮齿接触应力分布比较均匀，呈现一条斜线，分布在整个轮齿上，两端的轮齿接触应力比较大，应力分布线只占轮齿的一部分，而非啮合区域的轮齿则不产生应力。对于图6的主齿轮来说，最大接触应力发生在第三齿的齿顶部分，为854.12MPa，而对于图7的从齿轮来说，最大接触应力发生在第一齿的齿顶部分，为667.91MPa。

根据赫兹理论，斜齿轮疲劳强度校核公式为:

式中，ZE为弹性系数，ZH为节点区域系数，K为载荷强度系数，通过查表［10］分别为189.8，2.38，2.47。ZH为节点区域系数，Zε为重合度系数，Zβ为螺旋角系数，通过相关公式计算分别为0.812，0.974。经计算，求得斜齿轮接触疲劳强度为σH=933.86MPa，与有限元分析的最大应力误差为9.4%，在允许误差范围内。这是由于理论公式考虑了大量修正系数，而有限元分析精度相对来说较高造成的结果［11］。

主齿轮和从齿轮在最大负载的情况下产生的最大接触应力均没有超过材料的屈服极限1500MPa，因此可以看出齿轮的设计也是相对安全的，并不需要对齿轮的参数重新设计，但从接触应力云图来看，斜齿轮齿顶部分出现了应力集中现象，最大接触应力突然增大，容易导致齿轮突然折断或是塑性变形失效，从图8的安全因子来看，其值为0.978，处于危险的红色区域，因此有必要对斜齿轮进行去应力集中的措施。根据文献［12］，可以对斜齿轮轮齿进行齿廓修形，按照一定的规则改变轮齿齿顶渐开线的轮廓，降低应力集中。

3 斜齿轮齿廓修形

由于轮齿不同位置承受的载荷不同，在受力情况下啮合刚度发生了变化，这就使得齿轮的实际啮合点和啮合线理论啮合位置并不重合，导致轮齿局部载荷无法平稳过渡，产生应力集中和振动噪声，容易引起轮齿折断失效。为了预防失效，需要人为的将轮齿上单、双齿过渡点处发生干涉的齿面适当地削去一部分，人为地补偿轮齿的弹性变形，使得轮齿上的载荷平稳过渡，降低应力集中现象，这就是齿廓修形［13］。

3.1 齿廓修形参数确定

对于高频破碎器的斜齿轮来说，应力集中主要发生在齿顶部分，因此本次只对齿顶部分进行齿廓修形，齿根部分由于应力集中现象不明显，同时为了避免齿根弯曲强度削弱，因此不对齿根部分修形。斜齿轮的修形方式有两种，一种是斜修形，另一种是直修形［14］，考虑到斜齿轮实际加工的难度，本次选择直修形。

图9 齿轮齿廓修形方式

齿廓修形的参数有齿廓最大修形量、修形高度和修形曲线，最大修行量取决于齿轮的综合弹性变形，从上文斜齿轮啮合接触有限元分析结果中提取到主齿轮最大接触应力节点处的位移量J1为0.0436mm，对应的从齿轮节点位移J2为0.0272mm，齿轮的最大端面周向修形量和最大端面法向修形量公式分别为:

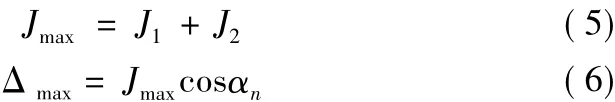
式中，Jmax为齿轮最大端面周向修形量，Δmax为齿轮最大端面法向修形量，αn为斜齿轮压力角。

根据式(5)、式(6)求得齿轮最大端面法向修形量为0.665mm，修形高度公式为h=0.5mn=3.5mm，修形曲线采用抛物线短修形形式［15］:

式中，l为沿啮合线上界点至啮合始点的距离，Δ为啮合线上相对于界点距离为x点的修形量。齿顶修形示意图以及修形后的三维图如图10所示。

图10 齿轮齿廓修形图

3.2 齿廓修形后的有限元分析

在只改变齿轮模型而不改变其他参数的情况下，对斜齿轮啮合进行有限元分析，主从齿轮的接触应力云图及安全因子云图如图11～图13所示。

图11 主齿轮接触应力云图

图12 从齿轮接触应力云图

图13 齿轮安全因子云图

表2 齿廓修形前后数据对比

从表2可以看出，经过齿廓修形后，齿轮啮合的最大接触应力从854.12MPa降低到了594.68MPa，降低了30.4%，去应力集中现象的效果非常明显，安全因子也提升到了安全范围内。从图11和图12来看，最大应力的发生点由主齿轮的第三齿转移到了从齿轮的第二齿，使得面积最大的第二接触线承载了更多的载荷，载荷分配更加合理。

4 结论

(1)运用计算机仿真技术，利用Solidworks、ADAMS、ANSYS Workbench这三个软件分别在建模、动力学仿真、有限元分析的优势，仿真得出斜齿轮轮齿所受的最大接触应力为854.12MPa，低于材料的接触疲劳极限，表明齿轮参数设计合理，满足寿命要求，为高频破碎器斜齿轮的设计提供了一种简单、直观的校验方法。

(2)通过有限元分析，其结果直观的反映了斜齿轮轮齿在啮合时接触区域的齿面接触应力分布，发现接触应力的最大值发生在单齿啮合时的齿顶部分，此处容易产生应力集中，其值相较于赫兹理论公式的计算，误差仅为9.4%，表明有限元分析的可靠性很高，具有很强的实用性。

(3)基于Workbench软件，通过对高频破碎器斜齿轮进行齿廓修形，改善了初始设计的斜齿轮易发生应力集中现象的状况，使最大接触应力降低了30.4%，提高了高频破碎器的使用寿命。

(4)通过动力学分析，反映出齿轮偏心块轮齿所受到的接触力Fn和驱动齿轮的转矩T并不符合传统的理论计算公式，即F，这是由于齿轮偏n心块产生的偏心力作用在了轮齿上面，因此在设计新齿轮时，必须考虑偏心块偏心力对斜齿轮轮齿受力时的影响。

［1］王开乐，杨国平，胡凯，等.高频破碎锤的发展现状与研究［J］.矿山机械，2015，43(4):1－4.

［2］刘涛，杨国平，曹国俊，等.基于ADAMS的高频破碎锤振动箱体的动力学分析［J］.矿山机械，2015，43(1):72－75.

［3］何文强，潘紫薇，罗铭.高频破碎器的力学性能分析［J］.工程机械，2015，46(8):28－33.

［4］李宁，李威.渐开线斜齿圆柱齿轮齿面接触强度分析［J］.机械传动，2014，38(3):151－153.

［5］谢最伟，吴新跃.基于ADAMS的碰撞仿真分析［A］.第三届中国CAE工程分析技术年会论文集［C］.2007，339－342.

［6］张学军，郭俊超.基于PRO/E与ADAMS二级行星齿轮传动系统的动力学研究［J］.组合机床与自动化加工技术，2015(3):93－96.

［7］范增辉，赵熙雍，宴红文.基于ANSYS的斜齿轮接触有限元分析［J］.机械传动，2010，34(4):68－70.

［8］孙林松，王德信，谢能刚.接触问题有限元分析方法综述［J］.水利水电科技进展，2001，21(3):18－20.

［9］刘爱敏，韩衍昭，王利红.斜齿轮传动啮合过程齿面接触应力有限元分析［J］.机械设计与研究，2013，29(3):35－38.

［10］濮良贵，纪名刚.机械设计［M］.8版.北京:高等教育出版社，2005.

［11］Seok-Chul Hwang，Jin-Hwan Lee，Dong-HyungLee.Contact stress analysis for a pair of mating gears［J］.Mathematical and Computer Modeling，2013(57):40－49.

［12］陈佳.考虑齿面及轴线偏差的斜齿轮接触有限元分析［D］.大连:大连理工大学，2009.

［13］吴勇军，王建军，韩勤锴，等.基于接触有限元分析的斜齿轮齿廓修形与实验［J］.航空动力学报，2011，26(2): 409－414.

［14］高小茜.风电齿轮箱轮齿接触有限元分析［D］.大连:大连理工大学，2008.

［15］李学智.船舶斜齿轮动力学分析及齿廓修形［D］.杭州:浙江工业大学，2015.

(编辑李秀敏)

The Gear Contact Stress Analysis and Tooth Profile Modification of High Frequency Knapper

LIU Wen，CAI Jia-bin，DING Cheng-bo，WANG Xing-wang
(School of Mechanical Engineering，Guizhou University，Guiyang 550025，China)

The vibration force of High frequency knapper is produced by the eccentric block on the helical gear，and the failure of helical gear can lead to high frequency knapper device not work normally.Helical gear three-dimensional model of the certain type high frequency knapper was established based on Solidw orks software accurately，and it was imported into ADAMS software for dynamic analysis，confirm the contact parameters，solve the output torque of the gear and meshing force，and then get parameters as the boundary conditions of finite element analysis，make tooth surface contact stress analysis in ANSYS Workbench，found that the helical gear meshing appeared stress concentration phenomenon，finally make a tooth profile modification for the helical gear addendum.The result show ed that the maximum gear tooth profile modification after contactstress reduced by 30.4%，and itprovides guidance for the design of high frequency knapper helical gear.

high frequency knapper;helical gear;dynamic analysis;the finite element analysis;tooth profile modification

TH122;TG506

A

1001－2265(2017)04－0060－05

10.13462/j.cnki.mmtamt.2017.04.015

2016－09－07;

2016－10－06

贵州大学创新基金(研理工2016029);面向智能装备领域的“技术众筹”研究生创新基地(贵大研CXJD［2015］003)

刘文(1991—)，男，土家族，湖南慈利县人，贵州大学硕士研究生，研究方向为CAD/CAM技术与应用，(E－mail)18798011213@163.

com;通讯作者:蔡家斌(1974—)，男，贵阳人，贵州大学副教授，研究方向为摩擦学与表面工程，(E－mail)734512130@qq.com。