基于反转法的超精密气体主轴回转精度测量不确定度研究*
2017-07-01陈衡胡秋许耀宇中国工程物理研究院机械制造工艺研究所四川绵阳62900国家机床产品质量监督检验中心四川四川绵阳62900
陈衡,胡秋,许耀宇(.中国工程物理研究院机械制造工艺研究所,四川绵阳62900;2.国家机床产品质量监督检验中心(四川),四川绵阳62900)
基于反转法的超精密气体主轴回转精度测量不确定度研究*
陈衡1,2,胡秋1,许耀宇1,2
(1.中国工程物理研究院机械制造工艺研究所,四川绵阳621900;2.国家机床产品质量监督检验中心(四川),四川绵阳621900)
为了评定超精密主轴回转精度准确度测量结果的分散性,在自主研发的气体静压主轴回转精度测试平台上进行了反转法测试,通过试验分析了影响测量结果的各不确定度因素及其相互影响关系,并提出了综合评估测量不确定度的完整流程。评定结果可作为仪器精度的现场评估、分析环境变化以及人员操作等对测量结果影响的依据,并为提高综合测量精度提供方向指导。
反转法;超精密主轴;回转精度;误差分析
0 引言
精密、超精密气体静压主轴在国防尖端技术、超精密加工装备等领域发挥着不可替代的作用,其回转精度可达亚微米、纳米级。主轴回转精度是评定机床动态性能的一项主要指标[1],其精确测量具有重要意义。传统测量回转精度多采用标准球打表法,其缺点在于用于精密、超精密气体主轴测试时标准球的安装偏心和形状误差将直接覆盖掉回转误差[2];而采用反转法的误差分离技术则可以分离标准球的形状误差[3],提高回转精度测量的准确性。
虽然理论上反转法能够完全消除标准球的形状误差,但是通过分析发现,在实际测量中,我们将不可避免的代入例如传感器测量球面靶标的非线性误差、传感器安装误差、环境影响等不确定因素的干扰。由于精密、超精密气体静压主轴的回转精度可达亚微米级,乃至纳米级,任何细小因素的引入都将可能影响测量结果的准确性。因此有必要综合考虑上述各不确定因素的影响,进行系统的不确定度评定,获得可靠的测量结果。
1 测量装置及方法
1.1 测量装置
本文测试所用气体静压主轴回转精度测试平台为自主研发装置,其结构如图1中所示,主要包括支撑架、测试平板、传感器调节组件、编码器调节组件、调心组件、标准球、电机、柔性联轴器等部件。测试平板通过水平调整件设置在支撑架上,在测试平板上表面分布有凹槽;传感器调节组件设置于凹槽之上,传感器调节组件能够调节传感器横向、纵向位置;待测主轴放置在测试平板中间孔端面上,其主轴上端设置有调心组件,调心组件包括编码器码盘、芯轴等,其上通过螺纹连接有标准球。柔性联轴器能够隔离驱动电机的振动和不同心引入的误差,调心组件具有调节标准球安装偏心、产生分度信号及索引信号的功能。本测试平台能够通过反转法分离标准球的形状误差,从而得到主轴回转误差。
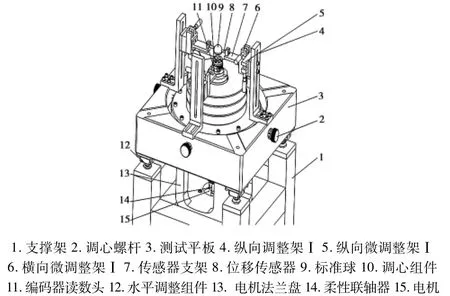
图1 气体静压主轴回转精度测试平台
本气体静压主轴回转精度测试平台最主要的功能部件为调心组件与柔性联轴器两个部分。其中调心组件含有主分度盘、螺钉、副分度盘、调整螺钉、码盘心轴、码盘、锁紧螺母以及法兰盘多个部分。图2的调心组件中的主分度盘外圆柱面设置有分度刻线,主分度盘内圆柱面与副分度盘的沉孔间隙配合,并通过副分度盘侧面的调整螺钉紧定,副分度盘通过螺钉与码盘心轴连接;码盘通过内圆柱面与码盘心轴的外圆柱面配合,并通过锁紧螺母压紧在码盘心轴台肩上,码盘心轴通过螺钉与法兰盘连接,所述的码盘不仅能够产生等分位置信号,每周还能产生一个索引信号。

图2 调心组件爆炸图
柔性联轴器(图3)本体为带有法兰安装面的圆柱状,在圆柱外表面交替切割成与轴线垂直的沟槽,在轴向形成柔性联接;在联轴器的另一端沿径向分布有两圈沿圆周均匀分布的沟槽,两圈沟槽分别与联轴器轴线同心,每圈沟槽沿圆周均匀分布为3段,外圈与内圈沟槽错开60°分布,在径向形成柔性联接。柔性联轴器的沟槽宽度应通过有限元刚度仿真确定,使其径向刚度、轴向刚度应小于待测气体静压主轴径向和轴向刚度的1/20。

图3 柔性联轴器
1.2 反转法测量实施例
在使用上述气体静压主轴回转精度测试平台采用反转法测量回转精度时,需设置2个传感器调整组件,且相对180°设置,见图1所示。本实施例利用调心组件将标准球同主轴回转轴线偏心尽量消除,然后调整传感器调节组件使传感器处于标准球表面最高点。具体步骤为:①安装固定一指示器(例如杠杆千分表)接触标准球下测量表面,利用电机驱动主轴,使标准球以较低速度匀速旋转,调整调心组件,直至指示器读出的数值波动范围不大于1μm,以尽量消除标准球同主轴回转轴线的偏心;②调整传感器调节组件,使传感器上下(或者左右)移动,直至传感器采集数据变为最大值时停止,然后在左右(或者上下)方向上重复上述操作,以保证传感器处于标准球表面最高点。
利用电机驱动待测主轴,使主轴匀速旋转,利用编码器索引信号作为采样启动信号,编码器脉冲为采样外部时钟。在电机运转30min后开始进行数据采集,每次测量以第20圈为采样结束点,每圈测量1024个点。测得采集完成传感器1数据m1(θ)之后,将调心组件主分度盘相对副分度盘旋转180°,再次驱动主轴匀速旋转,测得采集传感器2数据m2(θ),。对m1(θ),m2(θ)通过傅里叶级数展开,得到出去去除一次谐波和直流分量后的数据为T1(θ),T2(θ)。设标准球圆度为R(θ),回转误差为S(θ),则T1(θ)=R(θ)+S (θ);T2(θ)=R(θ)-S(θ),得出回转误差S(θ)=(T1(θ)-T2(θ))/2。
2 测量不确定度影响因素分析
测量过程中,可能导致测量不准的因素很多,主要包括以下几个方面:
(1)传感器测量球面靶标的非线性误差
本文通过试验验证获得了平板电容传感器测量球面靶标的非线性关系。试验方案如图4中所示。

图4 电容传感器测量球面靶标的非线性关系测定试验
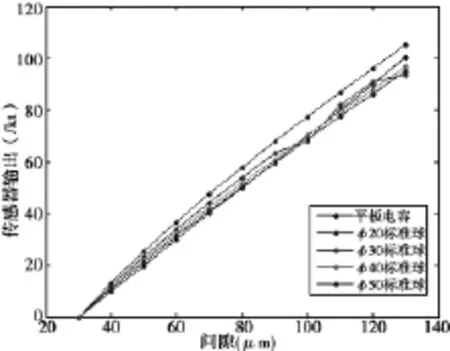
图5 平板电容测量球面靶标非线性曲线
通过试验获得如图5中所示的非线性关系曲线,可得出结论:目标物为球面时,传感器输出同实际位移呈非线性关系;传感器在不同初始位置测量输出与实际位移输入增益不同。因此在测量时,必须尽量限制标准球安装偏心,偏心量应控制在1μm以内(如图6所示,在初始间隙为20μm时,1μm对应的传感器增益非线性误差为0.41nm),否则将引入非线性误差;在采用反转法分离标准球面形误差时,同时必须保证传感器反转之后,初始间隙同反转前一致,否则也会引入非线性误差。

图6 初始位置20μm时电容传感器位移输出与实际输入的试验曲线
(2)电容传感器安装误差引起的测量误差
由于测量靶标为球体,电容传感器安装产生的偏移和倾斜误差都可以等效为偏移误差。仿真获得了电容传感器安装误差引入的非线性误差,如图7所示。传感器偏离球体中心时,传感器输出同实际位移呈非线性关系;这种非线性在小偏移量60μm内时,变化不显著。

图7 电容传感器偏移引起的位移输出
(3)环境因素对测量过程的影响
测量过程中,主要的环境影响因素包括温度和振动两个部分。而测试系统由多个具有不同热膨胀系数材料部件组成,各部件间装配关系复杂,采用理论求解难以获得准确的热变形。
根据分析得出,温度的影响主要来源于环境温度及电机运行产生的热量两个方面;振动的影响主要包括试验台地基振动与电机运行振动两个部分。在使用反转法进行数据采集时,实验环境温度始终控制在20℃±1℃范围内,而此时电机在运行30min后产生的热量及振动带来的影响都已达到一个恒定状态,且整个试验台进行过动平衡测试,电机空运转时测得的振动值与低速或高速运转时相差很小,可以近似忽略。为此在相同实验室测量环境中,以电动机空运行且主轴不转动情况近似模拟实际测试工况,连续监测标准球同传感器之间位移变化随时间和温度的变化情况,试验结果如图8a所示。
对实验时得到的数据进行傅里叶变换处理的结果如图8b所示,通过分析得出:环境因素的影响主要存在于0~5Hz、20~25Hz与45~65Hz三个频段。而20~25Hz与45~65Hz两个频段主要的影响因素为振动,0~5Hz频段的主要影响因素则为热变形。
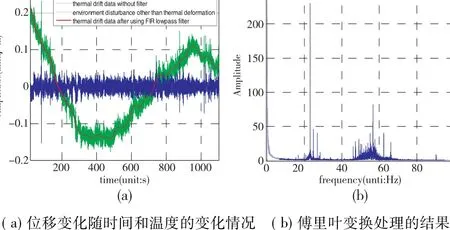
图8 主轴空运转情况下的环境因素影响情况
3 测量不确定度评定
3.1 不确定度评定过程
采用反转法进行回转精度测量时,首先需要对测量结果进行消偏心处理,之后进行误差分离,最后根据最小二乘圆法进行误差评定。进行不确定度评定时,本文采取与回转误差评定流程相同的程序进行分析,其具体过程如图9所示。

图9 回转误差评定流程
3.2 测量原始数据不确定度评定
根据2节中的测量不确定度来源分析,可以得到原始数据的测量模型为:
M(θk)=Probe(θk)+δlateral+δtilt+δvibration+δthermal(1)其中,M(θk)为传感器读数,Probe(θk)为传感器自身误差、δlateral为传感器测量球面靶标的非线性误差、δtilt为传感器安装引起的对准误差、δthermal为热变形误差、δvibration为振动误差。
由式(1)可得,原始数据的测量不确定度为:
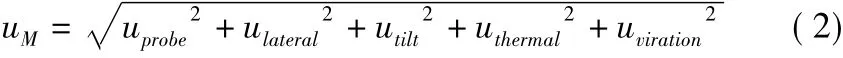
其中,uM为原始数据的测量不确定度,uprobe为传感器自身误差引起的不确定度分量、ulateral为传感器测量球面靶标非线性误差的不确定度分量、utilt为传感器安装误差引起的测量不确定度分量、uthermal为温度变化引起的测量不确定度分量、uviration为振动引起的测量不确定度分量。
3.2.1 与测量仪器相关的不确定分量
(1)由传感器自身测量误差引起的不确定度分量uprobe
采用的传感器经计量检定单位校准后所得的最大示值误差为20 nm,而传感器自身测量误差服从均匀分布,则由传感器自身误差引起的不确定度分量为:

(2)由传感器测量球面靶标非线性误差的不确定度分量ulateral
假设传感器测量球面靶标的非线性测量精度为α0的非线性测量误差在半宽α0/2的区间内服从均匀分布。由试验已知,在初始间隙为20μm时,移动1μm对应的传感器增益非线性误差为0.41nm。而在实际测量时,传感器与球面靶标之间的移动距离不会超过1μm,因此若标准球安装偏心量小于1μm且传感器测量球面靶标的非线性误差基本服从均匀分布时,传感器测量球面靶标非线性误差的不确定度分量为:

3.2.2 与测量过程相关的不确定分量
在传感器安装径向倾斜误差小于±0.5°,最大轴向误差小于0.4μm且横向初始间隙为20μm的情况下,传感器安装偏心对输出的影响在20nm以内,且传感器安装误差服从均匀分布,因此其引起测量不确定度分量为:

3.2.3 环境变化引起的不确定分量
(1)由温度变化引起的测量不确定度分量uthermal
在测量期间,环境、设备以及试验平台等都会产生漂移或变化,从而影响到测量系统的读数。估计在整个测量的时间段内,由环境波动所产生的测量值的最大漂移量为α1,做均匀分布处理。根据第2节中的环境试验得出:在30min内,受温度变化引起的热漂移影响,测量数据最多变化了62nm。因此由温度变化引起的测量不确定度分量为:

(2)由振动引起的不确定度分量uviration
在测量过程中,环境的振动会引起的试验平台和测量设备间的相对运动,从而导致测量结果分散。通常根据经验与现场测量可知,测量现场的振动引起的误差极限为α2,则可认为振动引起误差在半宽为α2/2的区间内服从反正弦分布。背景振动引起的测量不确定度能够通过统计方法获得,本文通过多次试验并经由滤波处理后的数据得出振动引起的测量不确定度分量u==9.2nm。
viration
将上述不确定因素全部带入式(2)中得到μm= 21.73nm。由于在进行数据采集时,每次测量都是以第20圈为结束点,为了更准确地评估回转运动误差,消除20圈里的积累误差,需将测量数据在不同20个测量圈数的每个相同样本点上做平均。因此平均回转误差的标准不确定度为==4.86nm。
3.3 消偏结果不确定度评定

本文采用平均消偏法消除测量原始数据中的一次谐波,其数学模型为:其中,M(θk)为测量原始数据,a1、b1为辨识得到的一次谐波系数,ε0为编码器分度误差引起的消偏残差,n为一周均匀采样点数,则a=1∑nM(θ)为测量
0n i=1k数据直流分量。
由于各被测点是在独立、等精度的条件下测量所得,因此各测量点间是相互独立的,得到消偏后结果的标准不确定度为:

3.4 反转法不确定度评定
反转法误差分离的不确定度模型为:

式中,r1(θ)和r2(θ)分别表示反转前后消除偏心的试验数据,εball和εsensor分别为反转后标准球与测头定位偏差引起的测量误差。由于r1(θ)和r2(θ)是相互影响的,很难以一个具有准确相对系数的解析表达式来表示与r1(θ)和r2(θ)相关的不确定分量,因此本文采用下式对其进行近似表达:

基于大量的模拟试验数据,本文运用蒙特卡罗法对uεball和uεsensor的数值进行分析。在标准球与测头定位偏差不大于0.2°的情况下,经过1000次模拟试验,得到εball为1.43nm,εsensor为1.62nm。然后根据式(11)计算得出经由反转法误差分离后的不确定度为5.39nm。
3.5 回转误差不确定度评定与验证
回转误差可用圆图法进行评价,其原理是将回转误差绘制成不同旋转角度下的极坐标曲线以直观的反映出回转轴线的运动曲线。因此回转误差可将总误差在圆周上平均以获得,其大小可以表述为以极坐标图最小二乘中心为圆心的同步误差曲线的最大内接圆和最小外接圆的径向距离。而最大内接圆和最小外接圆通常在不同的极坐标角度出现,因此将它们视为不相关,获得回转误差标准不确定度表达式为:

取扩展因子k=2,则得到采用反转法测量的回转精度的扩展不确定度为15.2nm。
为了确定反转法测量不确定度的准确性,本文使用了三点法对反转法测试结果进行了验证。为避免采用三点法测量时传感器自身特征的差异性引入的影响,整个试验过程只采用一个传感器进行数据采集。
分别采用反转法与三点法对同一静压主轴进行试验后得到的回转精度测量数据如图10所示,试验结果表明两种方法获得的回转精度差异非常小,最大差值仅为11nm。图11为分别使用反转法与三点法获得的标准球圆度,由图可知,两者之间最大差值为14nm。且使用反转法测量后分离出的标准球圆度为51nm,与标准球出厂精度50nm十分接近。并得到在扩展因子k=2时,采用三点法测量的回转精度的扩展不确定度为14.3nm,与反转法评定所得扩展不确定度仅相差0.9nm。

图10 反转法与三点法测量回转精度

图11 反转法与三点法测量标准球圆度
4 结束语
本文基于自主研发的气体静压主轴回转精度测试平台,运用反转法对超精密气体主轴的回转精度进行了测量,并对传感器测量球面靶标的非线性误差、电容传感器安装误差引起的测量误差以及环境因素的影响进行了深入和全面的研究。给出了一个完整的回转精度不确定评定过程,最终得出在扩展因子k=2的情况下,使用自研装置基于反转法测得气体主轴回转精度扩展不确定度为15.2nm,通过与三点法测量结果的比对,验证了评定结果的准确性。
[1]刘珊,宋微,段铁群.机床主轴回转精度在线检测研究[J].民营科技,2009(7):7.
[2]张明.空气静压主轴回转误差测量技术研究[D].绵阳:中国工程物理研究院,2008.
[3]苏文宇.主轴回转精度测试实验系统改造及其误差分析[D].哈尔滨:哈尔滨工业大学,2010.
(编辑李秀敏)
Uncertainty Evaluation of Aerostatic Spindle Rotation Accuracy by Donaldson Reversal Method
CHEN Heng1,2,HU Qiu1,XU Yao-yu1,2
(1.Institute of Mechanical Manufacturing Technology,China Academe Engineering Physics,Mianyang Sichuan 621900,China;2.National Machine Tool Production Quality Supervision Testing Center(Si chuan),Mianyang Sichuan 621900,China)
For assessing dispersiveness of measuring resultof rotation accuracy of high-precision aerostatic spindle,based on the test-bed for aerostatic spindle rotation accuracy w hich is independently designed and developed,some work is done for analyzing uncertain factors and their influence on the measuring result of rotation accuracy of high-precision aerostatic spindle,and then a comprehensive method for assessing the uncertainty of rotation accuracy is developed.Our research provides the basis for assessing local precision of Laser Tracker,and analyzing the influence of some uncertain factors(such as environmental change and personnel operation)on measuring resultes,and it is beneficial for improving comprehensive accuracy of measurement.
donaldson reversal method;ultra-precision spindlet;rotation accuracy;error analysis
TH115;TG506
A
1001-2265(2017)04-0010-04
10.13462/j.cnki.mmtamt.2017.04.003
2016-12-07;
2016-12-28
四川重点研发项目“精密、超精密机床运行状态精度检测技术与装置”资助(2017GZ0057)
陈衡(1990—),男,四川资阳人,中国工程物理研究院助理工程师,工学硕士,研究方向为机电控制及电气安全与电磁兼容检测,(E-mail)924256747@qq.com。
