“统计与概率”课程内容教学研究
2017-06-28李树臣
【摘要】为了引导学生学好“统计与概率”的有关知识,我们首先要了解这部分知识的主要内容,把握内容的主线、涉及到的核心概念,明确学习目标.然后精心设计问题情境,引导学生在经历知识的产生过程中掌握有关知识,在解决实际问题的过程中培养学生的应用意识,在对实际问题进行判断分析的过程中提高学生的推理能力,从而逐步形成数据分析观念和应用意识.
【关键词】核心概念;数据分析;应用意识;统计推理
《义务教育数学课程标准(2011年版)》(以下简称《课标(2011年版)》)在“课程设计思路”中安排了四个部分的课程内容:“数与代数”“图形与几何”“统计与概率”“综合与实践”[1].为帮助教师更好的引导初中学生学习“统计与概率”部分的有关知识,笔者在本文首先谈谈对这部分内容的认识,然后提出宏观教学建议.1全面认识“统计与概率”部分内容
1.1主要内容
“统计与概率”的主要内容有:收集、整理和描述数据,包括简单抽样、整理调查数据、绘制统计图表等;处理数据,包括计算平均数、中位数、众数、方差等;从数据中提取信息并进行简单地推断;简单随机事件及其发生的概率.
1.2內容主线
这部分课程内容的主线为[2]:
(1)数据分析过程:让学生参与收集、整理、描述和分析数据的活动,了解数据处理的过程;
(2)数据分析方法:掌握必要的收集数据、整理数据、描述数据和分析数据的方法;
(3)数据的随机性:体会样本和总体的关系.通过表格、折线图、趋势图等,感受随机现象的变化趋势;
(4)随机现象及简单随机事件发生的概率:通过列表、画树状图等方法列出简单随机事件所有可能的结果,以及指定事件发生的所有可能结果,从而了解并获得事件的概率.
1.3核心概念
《课标(2011年版)》提出了十个核心概念,本部分主要涉及三个:
(1)数据分析观念:了解在现实生活中有许多问题应当先做调查研究,收集数据,通过分析做出判断,体会数据中蕴涵着信息;了解对于同样的数据可以有多种分析的方法,需要根据问题的背景选择合适的方法;通过数据分析体验随机性,一方面对于同样的事情每次收集到的数据可能不同,另一方面只要有足够的数据就可能从中发现规律.数据分析是统计的核心[1].
(2)应用意识:结合“统计与概率”的知识,使学生经历收集数据、整理数据和分析数据的过程,让学生认识到现实生活中蕴涵着大量的和统计与概率有关的问题,这些问题可以用统计与概率的知识和方法加以解决,在解决的过程中逐步发展学生的应用意识.
(3)推理能力:推理是数学的基本思维方式,也是人们学习和生活中经常使用的思维方式.在“统计与概率”知识的教学中,结合具体内容,培养学生的统计推理能力.
1.4学习目标
初中阶段“统计与概率”部分的学习目标为[3]:体会抽样的必要性以及用样本估计总体的统计思想,进一步学习描述数据特征的方法,根据数据处理的结果做出合理的统计推断;进一步体会概率的本质含义,能计算简单事件发生的概率,能够应用概率的知识解决问题,体会统计与概率之间的联系,以及统计与概率在制定决策时的作用.
(1)经历数据统计的全过程(提出问题、确定样本、收集数据、整理和描述数据、分析数据、作出决策和预测);
(2)掌握统计与概率的一些基本知识和方法;
(3)感受客观世界的不确定性,初步形成对事件发生概率的认识;感悟一些随机现象的规律;
(4)运用统计与概率的知识和方法进行推理,作出合理的决策,并进行交流,逐步提高应用意识;
(5)能用随机的观念认识并解释现实世界,增强发现和提出问题的能力、分析和解决问题的能力;2宏观教学建议
统计和概率主要是通过对数据的收集、整理、描述和分析以及对客观事件发生可能性的刻画,来帮助人们更好的制定决策,这部分内容已成为一个公民的必备素养,是数学核心素养的重要组成部分.是义务教育阶段唯一培养学生用随机的观点来理解世界的课程内容,使学生掌握基本的统计与概率的知识和方法,形成数据分析的观念,在面对不确定情境或大量数据时,能作出更合理的决策,具有重要的教育价值[4]:
“数据分析观念”是统计和概率部分的核心,因为这部分内容与实际生活有着密切的联系,所以这部分内容的教学应围绕如何培养学生的数据分析观念及应用意识展开.
2.1经历知识的产生过程
在《课标(2011年版)》中,数据分析观念包含三层意思:
第一,经历数据分析的过程,体会数据中蕴涵着信息;
第二,掌握数据分析的基本方法,根据问题的背景选择合适的方法;
第三,通过数据分析,感受数据的随机性[2].
本部分内容“承载”着培养学生数据分析观念的任务,形成数据分析观念的有效方法就是让学生投入到数据分析的全过程中去.学生经历这样的过程,不仅能学习一些具体的知识和方法,同时还能体会到数据中蕴涵着大量有价值的信息,进而提高自己运用数据分析问题、解决问题的能力.教学中应“设计必要的数学活动,让学生通过观察、实验、猜测、推理、交流、反思等,感悟知识的形成和应用”[1].
案例1加权平均数概念的学习过程[5].
对于加权平均数的概念,教师可设计以下问题,让学生去独立思考、相互交流,进而发现新的知识.
(1)你过去已经学过平均数.你能举例说明如何计算一组数据的平均数吗?如果已知一组数据为x1,x2,…,xn,这组数据的平均数应该怎样计算?
(2)为满足顾客的需要,某商场将15kg奶糖、3kg酥心糖和2kg话梅糖混合成什锦糖出售.已知奶糖的售价为每千克40元,酥心糖为每千克20元,话梅糖为每千克15元.混合后什锦糖的售价应为每千克多少元?
小亮认为:混合后每千克什锦糖的售价是三种糖单价的平均数,即40+20+153=25(元).
小莹认为:在总体中三种糖的质量不相等,计算每千克什锦糖的售价时,应求出混合后三种糖的总价格,再除以它们的总质量数,即40×15+20×3+15×215+3+2=34.5(元).
你同意上面谁的算法?与同学交流.
(3)上面小莹列出的算式还可以作以下变形:
40×15+20×3+15×215+3+2=40×1520+20×320+15×220=34.5(元).
由此可见,什锦糖的单价不仅与混合前奶糖、酥心糖和话梅糖的单价有关,也与混合后这三种糖的质量在什锦糖质量中所占的比值有关.
(4)由问题(3)所列出的算式可以看出,数据40,20,15对什锦糖单价影响的“重要程度”是不一样的.你发现这三个数据影响平均数大小的“重要程度”可以通过哪三个比值反映出来?
(5)某车间工人日加工零件数如下表所示,仿照(3)中小莹列出的算式,你能计算出平均每个工人日加工零件的个数吗?
在这个问题中,数据20,22,24,25出现的次数是不同的,因此,全部数据的平均数,不仅受上述4个数据大小的影响,还要受到它们占这组数据总件数40的比值440,840,2040,840的影响.这就是说,这些比值的大小分别代表了上述四个数据影响平均数大小的“重要程度”.
因此,我们把比值440,840,2040,840分别称作数据20,22,24,25的权.
(6)在加权平均数的计算公式中,所有数据的权的和是多少?对比加权平均数与以前学过的平均数的意义,你能说出二者有什么联系吗?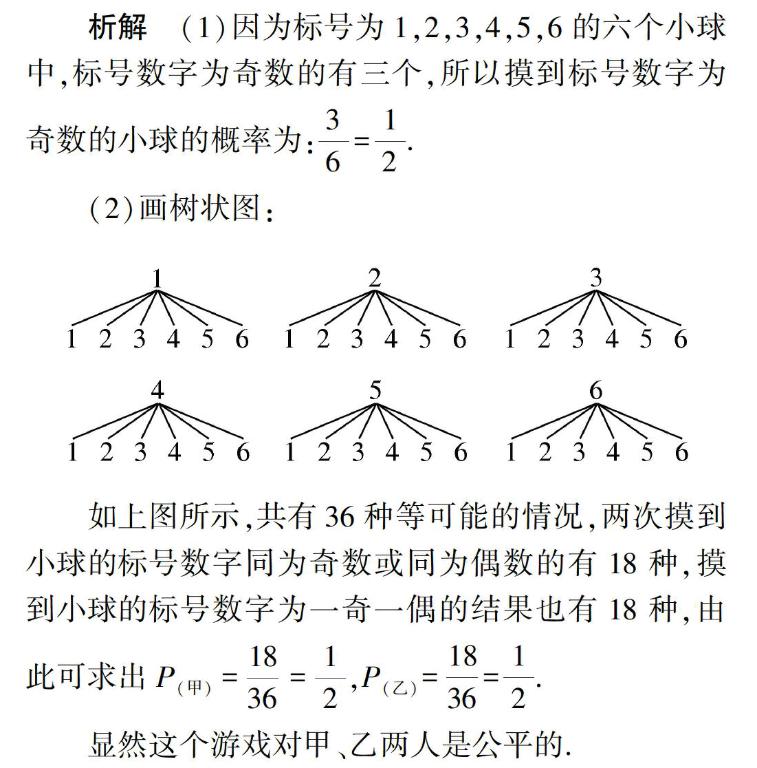
设计意图学生在小学第二学段已经学习了“平均数”的概念,问题(1)就是引导学生回忆这个问题的,本设计也就是在这个基础上产生的(这个基础本质上反映出引进加权平均数的可行性).为了体现《课标(2011年版)》提出的“现实性”要求,让学生加深对“数学来源于生活“的认识,设计了两个实际问题:第一个实际问题(求“什锦糖”的售价),这是个求平均数的问题.部分学生受思维定势的影响,可能会根据小学学过的平均数的求法,得到小亮的结果.为了让学生自己发现这种计算方法的错误,引起认知上的冲突,由小莹给出了另外一种计算方法.学生通过独立思考、相互交流能判断出小莹的解答是正确的.之后,通过对小莹列出的算式的变形,引出问题(3)中的算式,目的在于使学生感受到一组数据的平均数不仅与这组数中各个不同数据的大小有关,也与各个不同数据在总体中所占的比重,即各个数据影响平均数的“重要程度”有关.初步感受加权平均数中的“权”的意义.第二个实际问题,即问题(5)中计算“平均每个工人日加工零件的个数”,这也是个求平均数的问题.通过问题(5),学生再次感受到如果各个数据出现的次数与总次数的比值不同,在计算平均数时它们的重要程度也不相同(体现了引入新概念的必要性).因此,需要对学生原认知结构中平均数的计算方法进行加工改造,引出权的概念和加权平均数的计算公式,由平均数概念扩充到加权平均数概念及其求法,扩大了学生原有的数学认知结构.
2.2培养学生的应用意识
《课标(2011年版)》指出,数学教学应当“根据课程内容,设计运用数学知识解决问题的活动.……这样的活动要有利于提高发现和提出问题的能力、分析和解决问题的能力,增强应用意识和创新意识”[1].在“统计与概率”知识的教学中,应注重设计贴近学生生活的情境,使他们经历收集数据、整理数据和分析数据的过程,逐步发展应用意识[2].
案例2怎样的记分规则才合理[6].
青年歌手大奖赛的决赛在甲、乙两名歌手之间进行,9位评委的评分(10分为满分)情况如下表所示(单位:分):
(1)将甲、乙两名歌手的得分适当进行分组整理,并列成统计表;
(2)分别求出甲、乙两名歌手得分的平均数、中位数和众数;
(3)由(2)的结果,分析甲、乙两名歌手中谁的演唱水平较高;
(4)如果以平均分为标准区分比赛的名次,那么制订怎样的计分规则比较合理?
设计意图为培养学生能对日常生活中的有关统计问题做出分析判断,培养学生的数据分析观念和应用意识,特设计了以上四个问题:(1)要求学生先把题目中出现的评委对甲、乙两名歌手打分的原始数据适当进行分组、整理,并用统计图表分别描述;(2)分别计算两组数据的平均数、中位数和众数,使学生进一步感受这三个统计量计算方法的区别;(3)要求学生根据问题(2)的结果,利用平均数、中位数和众数对甲、乙的演唱水平进行评价,这实际上是对两组数据的集中程度从不同角度进行比较.学生通过解答这个问题,能认识到如果在一组数据中出现个别差异较大的数據时,用不同的统计量评价时,结果是不一样的.(4)制定计分规则是为了消除个别差异较大的数据对平均数的影响,采取去掉两个极端数据后再求平均数的方法,使评价的结果尽量做到客观公正,这实际上是对问题(2)中求平均数方法的改进.
2.3加强统计推理训练
统计推理是国际公认的统计学习目标之一,让学生具备根据不确定的情境做出决策以及处理统计信息的能力,是培养学生数学核心素养的重要措施之一.在“统计与概率”部分的教学中,应结合具体知识,对学生进行统计推理训练,不断提高学生的说理能力,从而实现《课标(2011年版)》指出的“了解利用数据可以进行统计推理,发展建立数据分析观念”[1]的课程目标.
案例3这种游戏公平吗?(2016年山东威海中考题)
一个盒子里有标号分别为1,2,3,4,5,6的六个小球,这些小球除标号数字外都相同.
(1)从盒中随机摸出一个小球,求摸到标号数字为奇数的小球的概率;
(2)甲、乙两人用这六个小球玩摸球游戏,规则是:甲从盒中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,乙再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判甲赢;若两次摸到小球的标号数字为一奇一偶,则判乙赢.请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平.
析解(1)因为标号为1,2,3,4,5,6的六个小球中,标号数字为奇数的有三个,所以摸到标号数字为奇数的小球的概率为:36=12.
(2)画树状图:
如上图所示,共有36种等可能的情况,两次摸到小球的标号数字同为奇数或同为偶数的有18种,摸到小球的标号数字为一奇一偶的结果也有18种,由此可求出P(甲)=1836=12,P(乙)=1836=12.
显然这个游戏对甲、乙两人是公平的.
启示本题是用概率的知识判断游戏的公平性问题.选材来源于学生的生活实际,符合学生的认知心理特点,这样的问题能激发学生的学习兴趣,调动其学习积极性.学生通过解答类似的问题,能“体会数学与生活之间的联系,运用数学的思维方式进行思考”,这对于培养学生的推理能力是大有帮助的,这种“以理服人”的好习惯、好品质也是基础教育的目的之一.
以上我们论述了引导学生学习“统计与概率”知识的宏观策略.在教学中要认真研读《课标(2011年版)》准确把握课程内容和教学目标要求,结合具体的知识内容,精心设计一些能利用这些知识进行统计活动的问题情境,引导学生经历观察、猜测、计算、推理等活动的过程.既重在实践,又重在综合,注重数学与生活实际、数学与其他学科、数学内部知识的联系和综合应用,感受数学的理性精神和人文价值[7].逐渐培养学生的数据分析观念以及应用统计与概率知识解决实际问题的能力,不断积累数学统计经验,逐步形成“评价与反思”的良好习惯和“严谨求实”的科学态度.
参考文献
[1]义务教育数学课程标准(2011年版)[S].北京:北京师范大学出版社,2012.
[2]史宁中.义务教育数学课程标准(2011年版)解讀[M].北京:北京师范大学出版社,2012.
[3]马复.初中数学教学策略[M].北京:北京师范大学出版社,2010.
[4]江守福.对数学课程标准中《统计与概率》部分的初步认识及教学建议[J].中学数学杂志,2002(2).
[5]李树臣.充分体现课标理念,促进学生全面发展——《义务教育教科书·数学》编写的主要原则[J].中学数学杂志,2015(8).
[6]展涛.义务教育教科书·数学八年级上册[M].青岛:青岛出版社,2013.
[7]李树臣.借鉴试题导学价值,提高数学教学质量——山东省青岛市2014年中考第23题赏析[J].中国数学教育,2015(11).
