“玩”出数学的本质

【摘要】对于天性爱玩的学生来说，在课堂中“玩”中学不失为一种有效的方法.课堂教学中的“玩”与“学”并不对立，它们相互融合不仅能给学生带来获取数学知识的快乐，还能充分激发学生参与数学学习的兴趣，更好地理解数学本质，提高数学课堂教学的质量.

【关键词】“玩”；三角形中线；数学本质

《数学课程标准》指出：“数学教学活动，特别是课堂教学应激发学生学习兴趣，调动学生积极性，引发学生的数学思考，鼓励学生的创造性思维.”枯燥乏味的数学内容，往往不能激发学生的学习兴趣，学生缺乏积极性和主动性，从而难以理解课堂中核心内容和数学本质.那学生怎样在课堂里快乐、轻松地学？怎样学得更好呢？对于天性爱玩的学生来说，在课堂中“玩”中学不失为一种有效的方法.课堂教学中的“玩”与“学”并不对立，它们相互融合不仅能给学生带来获取数学知识的快乐，还能充分激发学生参与数学学习的兴趣，更好地理解数学本质，提高数学课堂教学的质量.在此，本文试图通过《三角形的中线》的课堂教学，谈谈在课堂教学中怎样“玩”出数学的本质.1逸闻趣事──预设激趣，“玩”中思寻数学的本质

创设良好的情境，能激发学生的学习热情.而源于生活的逸闻趣事，可以把学生置于日常生活当中，做到数学生活化.学生看到、听到、想到的情境都是平时熟悉的事物，能更快地调动学生的积极性，活跃思维，很快进入学习的状态.加之教师形象生动的语言、恰当的姿势和手势，巧妙地设置一些悬念，设计一些思考性较强的问题，来激发学生的求知欲望，在“玩”中思寻数学的本质.

逸闻趣事：一则老人分财产、分土地的故事，玩一玩，猜一猜.

一位饱经苍桑的老人，经过一辈子的辛勤劳动，到晚年的时候，终于拥有了一块三角形的土地，由于年迈体弱，他决定把这块土地平均分给他的六个孩子，他是这样分的（如图1，D、E、F为BC、AC、AB的中点，S1、S2、S3、S4、S5、S6表示老大、老二、老三、老四、老五、老六的土地面积）

当六个孩子看到时，争论不休，都认为自己的地少.同学们，你认为老人这样分合理吗？为什么？

师：同学们，你猜一猜老人这样分合理吗？

学生格外兴奋，跃跃欲试.

生1：（把手高高的举起）我认为不合理，因为四块地形状不一样，四块地面积也不一樣.

生2：我认为合理，老大和老六的面积一样，老二和老四的面积一样，老三和老五的面积一样.

生3：我反对，这不能认为六块地面积一样啊.

面积一样吗？为什么呢？学生七嘴八舌争论起来，在猜玩中满脸笑容，但他们的眼神充满困惑.

师：大家遇到困难了吗？大家想不想学？

生：想.（大家迫不及待的大声回答）

师：为了解决这个问题，今天我们来学习新的内容.

设计意图面对新疑惑，学生这时处于一种复杂的心理状态，一方面学生非常想解决这个问题，很想说出为什么，另一方面又无法立即解决，因为认知水平不够，这种心理不平衡性激发了学生思寻问题的兴趣和热情，从而产生了强烈的求知欲，在大家的猜玩中，有利于新内容中数学本质的理解.2并肩作战──组内合作，“玩”中探究数学的本质

在初中数学课堂教学过程中，教师可从具体的教学内容出发，结合学生的实际，积极创设简单、生动有趣的“玩”的情境，以学生已有知识经验为起点，在小组内合作“玩”的过程中，引导学生探究数学的本质及解决问题的方案，使学生由被动地听讲变为主动地学习，充分调动学生的各种感官参与到“玩”的过程中，形成知识的表象，使学生分析问题、解决问题的能力得到进一步的提高.这样学生不仅理解掌握了数学知识，而且掌握了探究数学知识的方法.

游戏名称：并肩作战.

游戏内容：

（1）三角形的中线的定义是什么？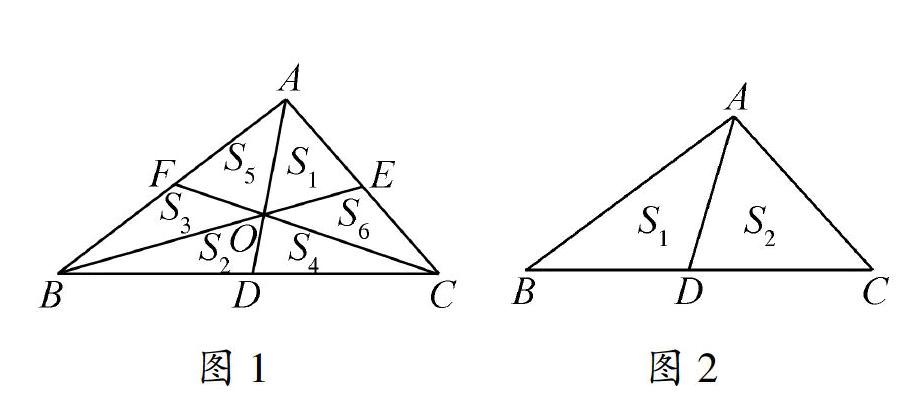

（2）如图2，D为BC的中点，S1、S2的面积有什么关系？请说出理由.

（3）把一块三角形分成面积相等的4部分，你有几种分法？

游戏要求：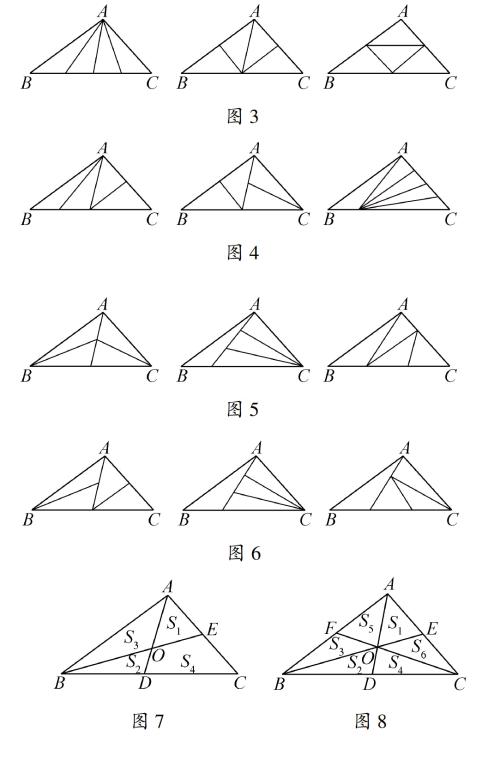

（1）让学生阅读教材，自己独立思考.（4分钟）

（2）学生进行小组合作讨论交流.（4分钟）

（3）各小组的讨论成果用小卡展示.（5分钟）

胜负规则：分法最多的小组获胜.

师：5-4-3-2-1.（时间到，老师发出结束口令）

师：同学们，三角形的中线的定义是什么？

生1：三角形的中线是连接△ABC的顶点A和它所对的边BC的中点D，所得线段AD叫做△ABC的边BC上的中线.

师：如图2，D为BC的中点，S1、S2的面积有什么关系？

生2：面积相等，因为等底同高等面积.

师：你能在黑板上做图示解释吗？

生：能.（同学很自信，快速在黑板作了解释，生鼓掌）

师：对于第③题哪些小组来展示你们的成果，看哪个小组的分法最多.（小组长踊跃举手示意）

师：很好，学习就需要这种精神.（师激励学生）现选举手的第1、2、3、4小组进行展示，其他同学记录与你们小组不同的方法.（被选小组代表迅速投影展示）

组1：把一块三角形分成面积相等的4部分，我们的分法有3种（图3）.

师：还有其它分法吗？

组3：我们的分法有6种，包含上面的3种（图4）.（第3小组有些迫不及待了）

师：还有其它分法吗？

组4：我们的分法有9种，包含上面6种（图5）.（第4小组信心满满的发言展示）

组2：我们的分法有12种，包含上面9种（图6）.（第2小组不甘示弱地讲起来）

同学们兴奋起来，小组同学有这么多种分法，真不可思议，给他们送上了热烈的掌声.

师：同学们太棒了，大家并肩作战，小组合作讨论，能玩出这么多分法，真叫精彩绝伦.大家思维非常开阔，真棒.我们应该从更深层次去挖掘，变换不同的角度去思考，才能使思考更完善，平时应养成这种好习惯.

师：哪个小组的分法最多？

生：第2小组.

师：第2小组方法最多，本轮游戏第2小组获胜.大家课后还可继续思考，还有很多分法.

设计意图通过小组合作的游戏形式，教师在教学中通过引导学生进行各种妙趣横生的探索，不但可以激发学生的学习兴趣，而且能使学生的思维纵横驰骋，创造力得到充分的发挥.为了抓住图形的本质特点，教师可多设计一些这样的练习，帮助学生透过现象抓住本质.3华山论剑──组间竞赛，“玩”中释疑数学的本质

学生在获取数学知识的过程中，对不理解的问题往往伴有“我要学会”、“我要弄懂”的欲望，具体的疑难之处，时常会给学生带来一种说不出的困惑，使学生产生一种似懂非懂的现象.这时教师可顺应孩子的天性，创设具体的学习情境，给学生提供“玩”的机会，使学生的疑难问题暴露在“玩”的过程之中，学生之间可以相互释疑解难，消除彼此间的学习疑惑，弥补自己知识的不足，从而找到解决知识难点的突破口，在“玩”中释疑数学的本质.

师：同学们，你们还敢挑战更有难度的题吗？

生：没问题，欢迎继续出题.（生很自信）

师：好，换个游戏.

游戏名称：华山论剑.

游戏内容：

（1）如图7，D、E为BC、AC的中点，哪些三角形面积相等？请说出理由.

（2）如图8，上课前提到的老人分财产、分土地的故事中，六兄弟的土地面积一样吗？请说出理由.

游戏要求：

（1）自己独立思考.（2分钟）

（2）学生进行小组合作讨论交流.（3分钟）

（3）各小组的抢答成果展示.（4分钟）

胜负规则：完成后抢答最快最准确的小组获胜.

师：5-4-3-2-1.（时间到，老师发出结束口令）

师：哪个小组来回答上面的问题？

组1：△ABD、△ACD、△ABE、△BCE面积相等.（第1小组迅速举手抢答）

组3：我要补充，还有S1=S2，S3=S4.因为S△ABD-S3=S△ABE-S3，以此类推.

师：老人分财产、分土地的故事中，六兄弟的土地面积一样吗？

组3：一样，根据上面的结论可知S△ABD=S△ACD=S△ABE=S△BCE=S△ACF=S△BCF，所以S1=S2=S3=S4=S5=S6.（还是被第3小组抢到了）

师：第3小组速度最快，而且准确无误，本轮游戏第3小组获胜.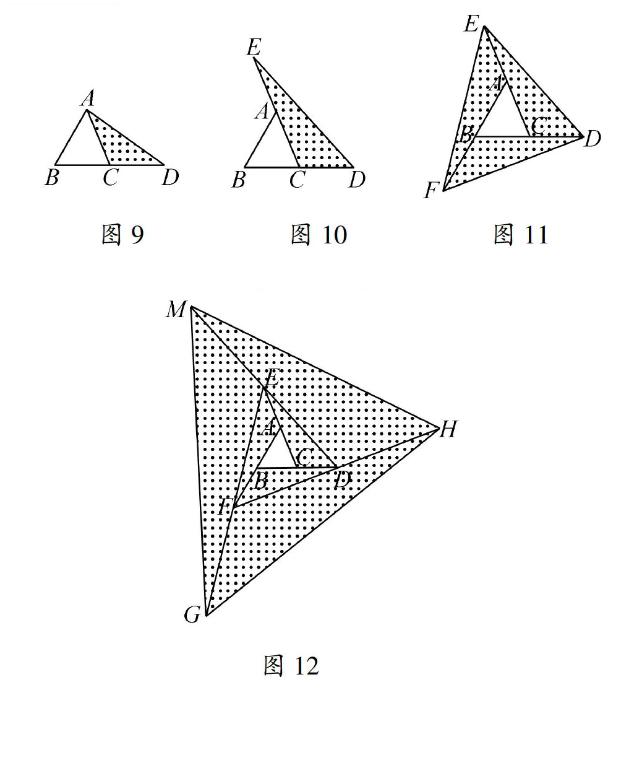

设计意图通过小组竞赛的游戏形式，学生始终保持着学习的兴奋状态，围绕题目进行多角度、多方向、多层次的变式思考与探索，加强不同知识点的纵、横联系，这样既可以节省学生的审题时间，提高教学课堂容量，也可以更大程度的提高学生思维的深刻性，有利于学生更扎实的掌握知识结论.4过关斩将──一题多变，“玩”中深化数学的本质

《数学课程标准》明确指出：“学生掌握数学知识，不能依赖死记硬背，而应以理解为基础，并在知识的应用中不断巩固和深化.”在数学课堂教学中，可借助游戏向学生传递知识和方法，借助游戏将数学知识拓展与深化，可以让枯燥无味的数学知识，变得好玩有趣.巩固练习时，多数是以做习题为主要手段来达到提高的目的，这种方式很容易引起学生的厌倦心理，往往达不到课堂教学的预期效果.新知探究后的巩固练习，应抓住学生的心理特点，适时创设游戏活动的情境，将数学知识融于整个游戏活动中，使游戏活动成为数学知识强化与拓展的平台.

游戏名称：过关斩将.

游戏内容：

在图9至图11中，△ABC的面积为a.

（1）如图9，延长△ABC的边BC到点D，使CD=BC，连结DA.若△ACD的面积为S1，则S1=（用含a的代数式表示）；图9图10图11

（2）如图10，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE.若△DEC的面积为S2，则S2=（用含a的代数式表示），并写出理由；

（3）在图10的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图11）.若阴影部分的面积为S3，则S3=（用含a的代数式表示）.

（4）像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF（如图11），此时，我们称△ABC向外扩展了一次.可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的倍.

（5）去年在面积为10m2的△ABC空地上栽种了某种花卉.今年准备扩大种植规模，把△ABC向外进行两次扩展，第一次由△ABC扩展成△DEF，第二次由△DEF扩展成△MGH（如图12）.求这两次扩展的区域（即阴影部分）面积共为多少m2？

游戏要求：

（1）自己独立思考.（3分钟）

（2）學生进行小组合作讨论交流.（3分钟）

（3）各小组回答正确才可继续作答.（5分钟）

胜负规则：准确回答问题最多的小组获胜.

设计意图通过过关斩将的游戏形式，调动学生学习的积极性和主动性，激发学生的求知欲.在“一题多变”的教学中，从不同角度组织感性材料，不断地变换事物的非本质属性，从而突出本质属性，并使有关的本质属性相互“联结”，形成“主心骨”，在“玩”中深化数学的本质，让学生领略“万变不离其宗”的奥妙.

总之，玩是一门艺术.“玩”让孩子们分散了学习的难点，分解了学习的压力；“玩”让他们自由创想，无羁翱翔，从作业堆中走出来，在自主、愉悦的氛围中学习有意义、有价值的知识.创设问题情境，让学生的兴致“高”起来；挖掘知识因素，让学生的感官“动”起来；开放想象空间，让学生的思维“飞”起来.对学生真正意义上减负增效，还他们一个自由快乐的求知殿堂！教师只有认真研究不同级学生的心理特点和认知规律，结合不同的教学内容，发掘生活中的数学资源，因时制宜、因地制宜地开展“玩”式教学，不断思考，大胆创新，在教学中把握点拨的时机，才能使学生真正在“玩”中用灵巧的双手发现学习的乐趣、用敏锐的眼睛捕捉学习的方法、用智慧的大脑思考学习的真谛.

参考文献

[1]郑强.初中数学课堂教学55个细节[M].成都：四川教育出版社，2006

[2]何乃忠等.新课程有效教学疑难问题操作性解读[M].北京：教育科学出版社，2007

个人简介孙树德（1983—），男，广东东莞人，中学一级教师.获得广东省初中青年数学教师优秀课评比“一等奖”，东莞市初中数学优秀课评选“一等奖”、东莞市初中数学优课评选“一等奖”，东莞市初中数学微课评选“一等奖”，东莞市初中数学现场片段教学“一等奖”，发表文章10余篇.