“统计与概率”综合复习
2016-03-04
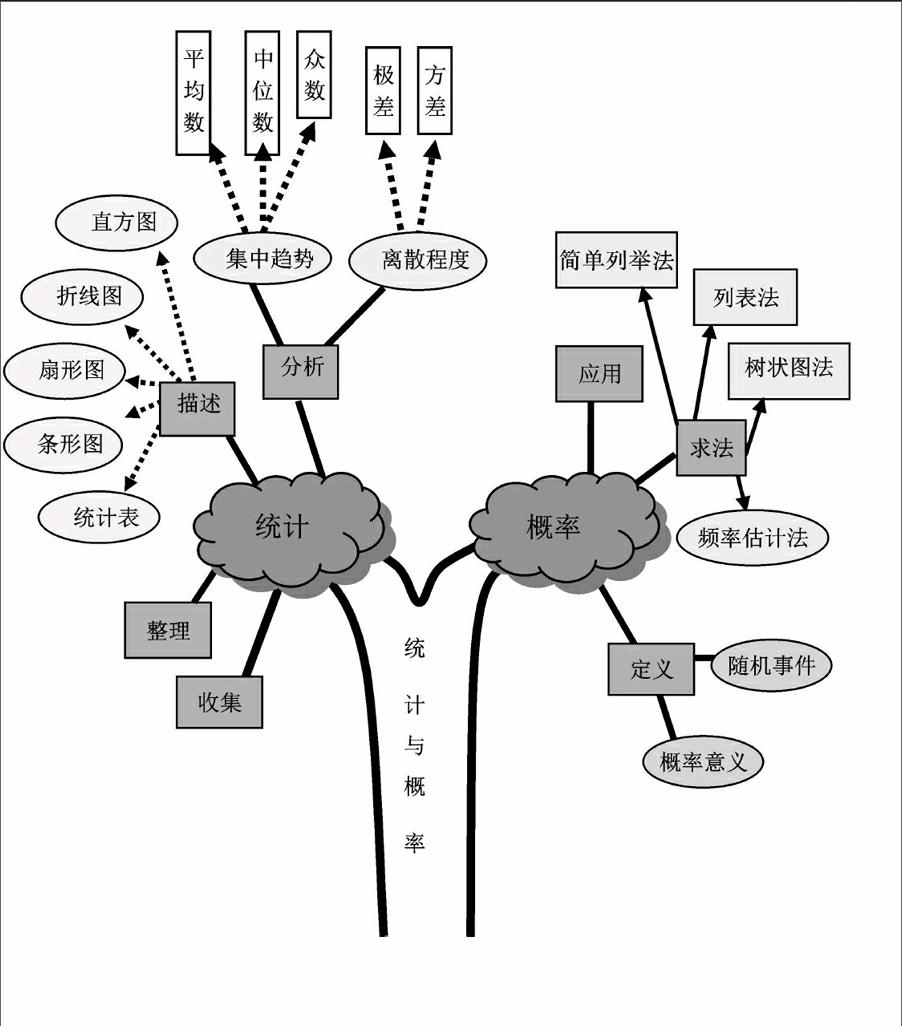
统计与概率在初中学习中占有重要的地位,从七年级教材就逐渐渗透,一直到九年级最后收尾,贯穿三年的学习.近几年这部分内容在中考中所占的比重也在逐渐增大,与实际生活的联系也逐渐增多.很多同学在刚刚学习统计概率时,由于对有些概念理解不清,或相关知识的要点把握不到位,或基本思想方法灵活运用不够,解题时常出现错误.现分析几种常见错误供大家参考,在解题中引以为戒.
一、 对统计中基本概念理解不深刻导致错误
例1 为了解某校2 000名师生对我市创卫生城市工作知晓情况,从中随机抽取了100名师生进行问卷调查,这项调查中的样本容量是( ).
A. 2 000名师生对创卫生城市工作的知晓情况
B. 100名师生
C. 100
D. 抽取的100名师生对创卫生城市工作知晓情况
【错解】样本容量是指从总体中抽取的样本数量,所以是100名师生.
【正解】从总体中抽取的样本个体的数目叫样本容量,指所要考察对象的数目,不带任何单位,故选C.
二、 对事件的概念把握不准造成分类错误
例2 下列事件中,属于不确定事件的有( ).
①太阳从西边升起;②从一副扑克牌中任抽一张是红桃;③掷一枚硬币,有国徽的一面朝下;④三角形内角和为180°
A. ②③ B. ①③④
C. ① D. ①②④
【错解】不确定事件是指事件一定不能发生,故选C.
【正解】不确定事件是指事件在发生前,事件的结果不能事先确定,也就是随机事件,不可能事件是一定不能发生的事件,事件在发生前就能确定结果,它是确定事件.解题中不能把不确定事件与不可能事件混淆,故选A.
三、 对统计图分析不仔细造成数据看错
例3 在一次捐款活动中,某班级有50名学生,将所捐款情况统计并制成统计图,根据图1提供的信息,捐款金额的众数和中位数分别是( ).
A. 20,20 B. 30,20
C. 30,30 D. 20,30
【错解】这组数据中,出现次数最多的是20人,故这组数据的众数为20.中位数是一组数据从小到大排列后,最中间的那个数.这组数据有50个,中位数是第25和26名职工捐款金额的平均数,(30+30)÷2=30,选D.
【正解】众数和中位数是指调查对象所记录的数据,不能把数据的个数当作调查的数据.本题是统计捐款钱数,30元出现次数最多,故本题答案是C.
四、 对统计图意义把握不准造成错误
例4 图2是甲、乙两户居民家庭全年支出费用的扇形统计图.根据统计图,下面对全年食品支出费用判断正确的是( ).
A. 甲户比乙户多
B. 乙户比甲户多
C. 甲、乙两户一样多
D. 无法确定哪一户多
【错解】一年中乙支出的百分比大于甲支出的百分比,故选B.
【正解】扇形统计图是为了反映各个部分占总体的百分比,计算各部分的量需用总体与该部分百分比相乘.本题没有明确甲乙两家全年的具体收入,所以无法算出食品支出的具体费用,无法比较,故本题正确答案是D
五、 对机会的等可能性理解不够导致树状图画错
例5 在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个,若从中摸出一个球,放回搅匀,再摸另一个球,求两球颜色相同的概率.
【错解】画树状图如下:
可得两球颜色相同的概率.
【正解】箱中三种颜色的球数目不相同,所以在摸球过程中被摸到的机会是不均等的,本题红球被摸到的机会大于黄球、蓝球,所以在画树状图时应该把它们转化为均等机会.正确的树状图如下:
由树状图可得两球颜色相同的概率为.
六、 对等可能性事件发生的机会和事件最终结果混淆造成错解
例6 掷一枚硬币,连掷三次,求有两次正面向上的概率( ).
A. B. C. D.
【错解】三次抛出的结果分别是:正正正,正正反,正反反,反反反四种情况,其中出现两次正面向上的情况只有一次,故概率为,选B.
【正解】随机事件的概率,是把事件在发生过程中所有可能发生的均等机会,与满足一定条件的机会相比较,不能把事件的最终结果当作机会.正确的解答要通过画如下树状图:
由树状图可求得两次正面向上的概率为.
七、 对模拟实验的条件选择不合理造成错误
例7 端午节,妈妈为洋洋准备了4只粽子:一只香肠馅,一只红枣馅,两只什锦馅,4只粽子除内部馅料不同外,其他都相同.洋洋喜欢吃什锦馅的粽子.
在吃粽子之前,洋洋准备用如图3所示的转盘进行吃粽子的模拟试验(此转盘被等分成四个扇形区域),规定:连续转动两次转盘表示随机吃两只粽子,从而估计吃两只粽子刚好都是什锦馅的概率.转盘是一个放回的实验,故第一次转到什锦(或香肠、或红枣)后第二次还能转到.
【错解】画模拟试验的树状图为:
所以有16种情况,其中两次都是什锦馅的有4种情况,所以概率为.
【正解】设计模拟实验计算随机事件的概率,要分清事件的条件,事件发生的方式,事件结果.在设计模拟实验工具时必须与原事件相关事项保持一致.本题从4只粽子中吃两只粽子是一个不放回问题,而转盘是一个放回问题,所以不能以转盘代替.正确的树状图应该为:
∴P(吃到两只粽子都是什锦馅)==.
诸如以上常见错误,都是同学们在学习过程中不注意把握好基本概念的本质,解题中不注意应用基本方法,解题时分析问题不仔细等一些原因造成的,只要同学们在学习过程中把握好知识的本质要点,解题中分清问题的条件,再加上细心,就可以避免出错了.
(作者单位:江苏省宿迁市宿豫区实验初级中学)
