上海市原静安区成人流感样病例就诊百分比预测的自回归求和滑动平均模型构建与应用

沈冰+沈磊+倪晓芬

摘要： 目的 探讨构建并应用自回归求和移动平均（autoregressive integrated moving average， ARIMA）模型预测原静安区成人流感样病例（influenza-like illness， ILI）就诊百分比的可行性。

方法 基于2011—2014年上海市原静安区的逐月成人ILI就诊百分比，模型参数确定采用非条件最小二乘法，模型结构依据简洁与残差不相关原则确定，拟合优度以许瓦兹贝叶斯准则与赤池信息准则评估，构建成人ILI就诊百分比预测的最优ARIMA模型。以模型预测原静安区2015年1—10月成人ILI就诊百分比，计算实际值与预测值的相对误差；并预测原静安区2016年的成人ILI就诊百分比。

结果

模型ARIMA（0，2，1）（1，1，0）12（无常数项）对成人ILI就诊百分比时间序列拟合良好，移动平均参数（MA1=0.944）与季节自回归参数（SAR1=-0.542）有统计学意义（P<0.001），残差达到白噪声（P>0.05），模型表达式为（1+0.542B）（1-B）2 （1-B12）Zt=（1-0.944B）μt。2015年1—10月的成人ILI就诊百分比的預测值符合实际值的变动趋势，相对误差最小仅为4.45%。

结论 ARIMA模型可以较好地拟合原静安区成人ILI就诊百分比的时间变动趋势，能对成人ILI就诊百分比进行预测，短期预测有较高的精度。

关键词： ARIMA模型； 成人流感样病例； 就诊百分比； 预测中图分类号： R 183.3 文献标志码： A

Abstract： Objective To explore the feasibility of constructing and applying the autoregressive integrated moving average（ARIMA）model for predicting the hospital-visiting percentage of adult influenza-like illness （ILI） in Jing-an District， Shanghai.

Methods An optimal ARIMA model for predicting the hospital-visiting percentage of adult ILI was established based on the monthly hospital-visiting percentage of adult ILI in Jing-an District of Shanghai from 2011 to 2014. The parameters of the model were determined through non-conditional least square method， the structure thereof was determined according to the concision principle and residual non-relevance principle， and the goodness of fit thereof was determined in accordance with Schwarz Bayesian Criterion（BSC） and Akaike Information Criterion （AIC）. This model was applied to predict the monthly hospital-visiting percentage of adult ILI in Jing-an District from

January to October of 2015 and to calculate the relative error between the actual value and the predicted one； it was also used to predict the monthly hospital-visiting percentage of adult ILI in Jing-an District in 2016.

Results

The ARIMA model （0，2，1）（1，1，0）12 （without constants） could well fit the time series of the hospital-visiting percentage of adult ILI while both the moving average coefficient （MA1=0.944） and the seasonal autoregressive coefficient （SAR1=-0.542） had statistical significance（P<0.001） and the residual error reached white noise（P>0.05）. The mathematic expression of the model was （1+0.542B） （1-B）2 （1-B12）Zt=（1-0.944B）μt. The predicted value for the hospital-visiting percentage of adult ILI from Jan.， 2015 to Oct.， 2015 was in conformity with the change trend of the actual value and the minimal relative error was only 4.45%.

Conclusion The ARIMA model can well fit the time-change trend of the hospital-visiting percentage of adult ILI of Jing-an District and can be used to forecast the hospital-visiting percentage of adult ILI while ensuring relatively high accuracy of short-term forecasts.

Keywords： ARIMA model； adult influenza-like illness； hospital-visiting percentage； forecast

流感样病例（influenza-like illness， ILI）是指体温高于38℃，同时伴有咽痛或咳嗽，而其他实验室诊断结果缺乏者。原静安区是上海市的中心城区，人口密度大，ILI是辖区内常见的一种急性呼吸道传染病。自回归求和移动平均（autoregressive integrated moving average， ARIMA）模型属于时间序列分析的一种，随着传染病防治研究的深入，越来越多的研究将其应用到传染病预测[1-3]。本文采用ARIMA模型对上海市原静安区哨点医院门诊每月成人ILI就诊百分比数据构建预测模型，并对2016年原静安区成人ILI就诊百分比開展外部预测，以评价该模型应用于成人ILI就诊百分比的短期预测价值，为科学开展流行性感冒的预防控制提供可借鉴的依据。

1 资料与方法

1.1 资料来源

开展预测成人ILI就诊百分比的监测资料，来自2011年1月—2014年12月上海市原静安区哨点医院发热门诊的每周ILI就诊数和门急诊就诊病例总数，将每周的数据进行整理，以每月的ILI就诊百分比为单位进行模型拟合与预测。

1.2 研究方法

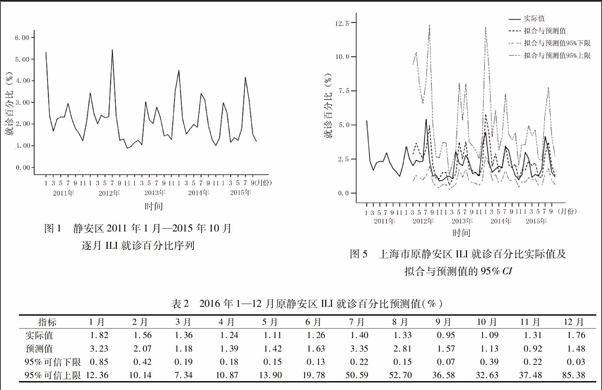
本研究对ILI就诊百分比数据使用时间序列分析中的ARIMA模型进行拟合与预测。通过平稳序列、模型识别、参数确定和模型诊断、预测4个步骤进行建模。模型结构为ARIMA（p，d，q）×（P，D，Q）S，其中自回归及移动平均的阶数分别设为p、q，差分次数为d，季节性自回归及移动平均的阶数分别设为P、Q，季节性差分次数为D，季节周期设为s。模型拟合的数据来自2011年1月—2014年12月的监测点ILI就诊百分比，模型的预测效果以2015年1—10月的逐月ILI就诊百分比进行回代评价，预测精度以ILI就诊百分比实际值与预测值的相对误差评价，最后以2011年1月—2015年10月的每月ILI就诊百分比建模预测2016年1—12月的ILI就诊百分比。

1.3 统计学分析

采用SPSS 22.0软件构建逐月ILI就诊百分比原始数据库，采用Time Series预测模块开展模型拟合与数据处理。

2 结果

2.1 平稳序列

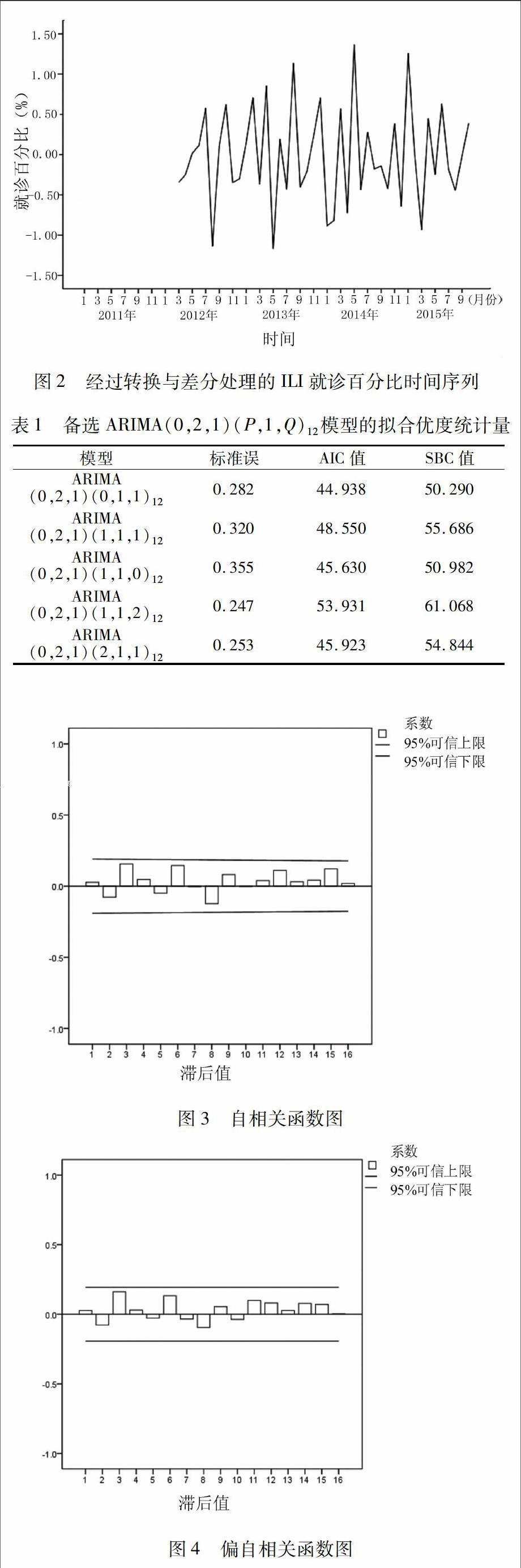
将2011年1月—2015年10月的每月ILI就诊百分比制成时间序列图（图1），从序列图中发现ILI就诊百分比序列在2013年以前数据变异较大，序列的前后差别较明显，季节周期性变化也较明显，每年有冬季和夏季2个高峰。采用自然对数变换将原始数据转变为方差平稳的序列，为避免趋势及季节的影响，再进行2次一般差分及1次季节差分，最终原始数据转换为1个较平稳的随机序列（图2），满足了ARIMA模型平稳性的前提。

2.2 模型识别

根据上述处理步骤，明确了本模型应为复合季节模型ARIMA（p，2，q）（P，1，Q）12，结合了季节性模型与连续性模型的特征，且模型周期为12个月。p、q值依据自相关及偏自相关函数分别定为0、1，即ARIMA（0，2，1）（P，1，Q）12。P、Q值则应分别取0、1、2进行拟合以获得最佳结构模型。

2.3 模型参数确定和模型诊断

参数确定依据非条件最小二乘法，以10为模型计算时的最大迭代次数。表1显示了相关备选模型的拟合优度统计量。对模型进行诊断时包括检验拟合优度、参数有无统计学意义、检验参数独立性和残差检验4方面。较优模型评价的准则为贝叶斯SBC值及赤池AIC值都较小，以此为判断标准，同时考虑模型参数的统计学意义，获得较优模型ARIMA（0，2，1）（1，1，0）12。由于该模型常数项没有统计学意义（P=0.362），不符合模型对简洁性的要求。因此，将常数项去除，再次拟合模型ARIMA（0，2，1）（1，1，0）12，所得模型的MA1与SAR1参数值分别为0.944和-0.542，均有统计学意义（P<0.001），模型拟合优度高于早先的较优模型ARIMA（0，2，1）（1，1，0）12，标准误为0.362，SBC与AIC值分别为44.598和48.167。经检验参数独立性，ARIMA（0，2，1）（1，1，0）12（非常数项）的各项参数间无显著相关性，相关系数rMA1，SAR1低至0.07。同时，模型残差序列的自相关与偏自相关函数均未超越可信限（图3、图4），提示模型为随机残差。经检验，Box-Ljung统计量均无统计学意义（最小Box-Ljung为0.006，P=0.939），提示残差为白噪声，残差的独立性好。

通过对模型的诊断，得到最优模型为ARIMA（0，2，1）（1，1，0）12（非常数项），以后移算子表示为：（1-Φ1B）212Zt=（1-θ1B）μt，将参数代入方程，得模型方程为：（1+0.542B） （1-B）2 （1-B12）Zt=（1-0.944B）μt ， Zt为每月ILI就诊百分比的自然对数。

2.4 回代模型及外推预测

以最优模型ARIMA（0，2，1）（1，1，0）12（非常数项）对2011年1月—2014年12月的逐月成人ILI就诊百分比进行拟合，并预测2015年1—10月的ILI就诊百分比（图5）。图5展现了模型拟合2011年1月—2014年12月的结果，以及预测2015年1—10月的结果，可见模型对实际ILI就诊百分比的拟合及预测结果良好，拟合值与预测值的动态趋势大致符合实际值。各月预测值与实际就诊百分比的差距很小，2015年1—10月期間，ILI就诊百分比的预测值与实际值的相对误差最小，仅为4.45%，最大为43.11%。之后以2011年1月—2015年10月的数据重新拟合模型ARIMA（0，2，1）（1，1，0）12（非常数项），并外推预测2016年1—12月的ILI就诊百分比。预测结果见表2，每月的ILI就诊百分比波动在0.92%～3.35%之间，冬季和夏季各有1个高峰，分别为1月的3.23%和7月的3.35%，与目前的实际情况相符。

3 讨论

ARIMA模型是时间序列分析中的一种常用模型，近年来，该模型在传染病预测、预警领域应用较为广泛，特别适合于预测具有不典型特征，且判别困难的时间序列资料[4]。模型有综合评估时序数据的随机干扰、趋势性与周期性的优点，并以模型参数对其进行定量。当实际工作中，对监测数据的变化趋势的主要影响因素很难判断，也无法找到有关的数据时，ARIMA模型就特别具有其使用的优越性[5]。该模型的短期预测精确度相当高。ILI就诊百分比是间接反映流感流行强度的一个症状监测指标，该指标具有一定的季节周期性，但时间序列的特征并不典型。对成人ILI就诊百分比的预测具有前瞻性意义的研究，通过将常规监测与模型预测有机结合，有利于及时发现异常的变化情况。不同模型的预测效果与其应用条件相关联， ARIMA模型可以不考虑影响ILI就诊相关因素各自的效应，而是将其统一纳入时间变量中进行综合分析，相对于其他预测模型具有更高的短期外推预测精度。

原静安区成人ILI就诊百分比的时间序列图显示变异较大，且有较明显的季节性周期变化，呈非平稳的时间序列。因此，建模前应先进行序列平稳化，以满足模型拟合的前提。原始数据经过自然对数变换以平稳方差化后，再通过2次一般差分与1次季节差分，从而获得了接近平稳的1个随机序列。然后，依次通过模型识别与诊断，确定了最优模型ARIMA（0，2，1）（1，1，0）12（非常数项）。模型较好地拟合了成人ILI就诊百分比的各项实际值，获得的2015年1—10月ILI就诊百分比回代预测值与实际值具有较好的一致性，说明采用ARIMA模型预测成人ILI就诊百分比重复性优、可靠性好。最后将2011年1月—2015年10月的数据建模并外推预测2016年的ILI就诊百分比，模型拟合效果的验证理论上严谨，应用上可行。影响成人ILI就诊的因素比较多，并且互相之间影响，本研究获得的预测值是以数学模型为基础的理想值，有可能与实际值呈一定的差异，但不失为ILI预警的一项科学依据，并能进一步为流感的防控提供指导方向。

参考文献

[1]LIU Q，LIU X，JIANG B，et al.Forecasting incidence of hemorrhagic fever with renal syndrome in China using ARIMA model[J].BMC Infect Dis，2011，11： 218.

[2]EARNEST A，CHEN MI，NG D，et al.Using autoregressive integrated moving average （ARIMA） models to predict and monitor the number of beds occupied during a SARS outbreak in a tertiary hospital in Singapore[J].BMC Health Serv Res，2005，5：36.

[3]QUENEL P，DAB W. Influenza A and B epidemic criteria based on time series analysis of health services surveillance data[J].Eur J Epidemiol，1998，14（3）：275-285.

[4]ALLARD R. Use of time-series analysis in infectious disease surveillance[J].Bull World Health Organ，1998，76（4）：327-333.

[5]谭莘，田考聪. 数学模型在人群疾病预测研究中的应用[J].中国医院统计，2005，12（1）：83-85.

（收稿日期：2016-12-19）