直角坐标系中两条直线的特殊位置关系的特点及其应用

湖北省孝感市大悟县四姑镇中学 吴胜祥

直角坐标系中，有两条直线，设y1=ax+ m, y2=bx+n ，有时，a=b；y1⊥y2时，ab=-1。反之有：a=b时，y1Py2；ab=-1时，y1⊥y2。下面利用这些性质解题。

一、利用一次函数一次项系数相等证明两直线平行

例题：已知直线为y=2x+3与双曲线的图像交于A、B两点，A在第一象限，过A作AE⊥y轴于E，过B作BF⊥x轴于F，连接EF。（1）求证：AB//EF。（2）求△ABE的面积。

解：（1）由得

∴A（1,5）

又AE⊥y轴于E，∴E（0,5）。BF⊥x轴于F，∴F0）。

设yEF=k x+b，∴b=5

∴k+b=0 ∴k=2

∴yEF=2 x+5

又2=2 ∴yEF∥yAB，

即AB||EF。若E在x轴上，F在y轴上，同理AB||EF。

（2）

二、利用两个一次函数的一次项的系数互为倒数证明两直线垂直

例题：（2015年湖南衡阳）如图，顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点，且A在x轴上，点B的横坐标为2，连接AM、BM。

（1）求抛物线的函数关系式.

（2）判断△ABM的形状，并说明理由。

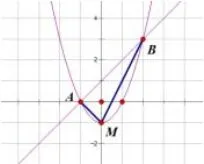
解：（1）∵A在x轴上且在直线y=x+1上

∴A（-1,0） 又B在直线y=x+1上且横坐标为2，则B（2,3），又抛物线顶点M在y轴上，设y=ax2+k 有

∴抛物线y=x2-1

（2）有y=x2-1知顶点M的坐标为（0，-1），设yAM=k x+b过点M，∴b=-1，又过A（-1,0）∴-k-1=0 k=-1。∴直线yAM=-x-1。又1×（-1）=-1，∴AM⊥AB ∴△ABM是直角三角形。

三、利用两直线垂直的特点求坐标系中矩形折叠问题的点的坐标

例题：（2015，北海）如图在矩形OABC中，OA=8，OC=4.沿对角线OB折叠后，点A与点D重合，OD与BC交于点E。求点D的坐标

解：∵四边形OABC是矩形，OA=8，OC=4.

∴B（8,4） A（8,0）∴,又A与D关于OB对称。

∴A D⊥O B。设yAD=-2x+b过 A（8,0），

∴0=-2×8+b ∴b=16

∴yAD=-2x+16。

又由折叠性质知B E=O E，设CE=x，则OE=BE=8-x。又∠OCE=900O C=4，∴(8-x)2=x2+42∴x=3∴E（3,4）。∴令-2x+16，得。又时，∴D点坐标为。

四、利用两条直线垂直的特点求直线与抛物线交点的坐标

例题：如图，直线y=x+2与抛物线y=ax2+bx+6（a≠0）相交于和B( 4,m)，点P是线段AB上异于A、B的动点，过P点做PC⊥x轴于点D，交抛物线于点C。（1）抛物线的解析式。

（2）求△PAC以A为直角顶点时点P的坐标。

解：（1）∵B（4，m）在直线y=x+2上，∴B（4,6）

又且A、B在抛物线y=ax2+bx+6上，

则有：

得

∴抛物线y=2x2-8 x+6。

（2）∵P在AB上，PC||y轴交抛物线于C

∴△P A C是以A点为顶点的直角三角形时，A B⊥A C。又yAB=x+2，设yAC=-x+b ，过∴∴b=3 ∴yAC=-x+3.令2 x2-8 x+6=-x+3得（舍去）.x2=3又x=3时，y=x+2=5，所以△PAC以A点为直角顶点时P点的坐标为P（3，5）。

五、利用坐标系中两直线平行的特点求直线与抛物线交点坐标

例题：（2016，十堰）已知抛物线y=ax2+bx+c 与x轴交于点A（-1,0）、B两点（点A在点B的左边），其顶点为M（1,4）。MA交y轴于N，连接OM。

（1）求此抛物线的函数表达式。

（2）若P为（1）中抛物线上一点，当SDOAM=SDPAM时，求P点坐标。

（3）将（1）中的抛物线沿y轴折叠，使A落在点D处，连接MD，Q为（1）中抛物线上一点，直线NQ与x轴交于点G。当Q点在抛物线上运动时，是否存在点Q，使得一A、N、G为顶点的三角形与△ADM相似？若存在，求出符合条件的Q的坐标，若不存在，说明理由。

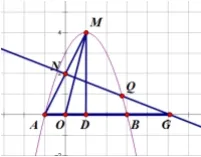
解：（1）∵抛物线的顶点M（1,4） ∴0=a (-1- 1)2+4得a=-1

∴抛物线的解析式为y=-x2+2 x+3

（2）∵A（-1,0） M（1,4） ∴易求过O点作OE||AM，则∴

∴当时，当时，此时点P的坐标为或又直线AM与y轴交点N的坐标为（0,2）∴直线yOE=2x关于直线AM对称的直线解析式为y=2x-4.令-x2+2 x+3=2 x+4，此时无解。∴当时，P点的坐标为

（3）∵点A关于y轴对称点D的坐标为（1,0），又M（1,4）∴MD⊥x轴。∴△ADM是以D为直角顶点的直角三角形。

当∠AGN=∠ADM=900△ANG∽△ADM，此时点G与点O重合，则Q点坐标为（0,3）

当∠A N G=∠A D M=9 00时，△ANG∽△ADM，此时QG⊥AM。设，过点N（0，2） ∴2×0+b∴b＝2∴令x+2=-x2+2 x+3∴∴当时，当时，。∴当△ANG∽△ADM时，Q点坐标为，

教师教书的过程也是教师对教学不断自我总结的过程，利用两条直线的特殊位置关系解题，可以少作辅助线，使得图形的计算简化，公式化，通过两条直线平行或垂直的特点可以很容易地求出另一条直线的解析式，然后利用直线与直线，直线与抛物线建立方程或方程组，从而很直观地求出图像中有关交点的坐标。同时，也可以利用两个一次函数的一次项系数的特点证明两直线平行或垂直。