非十进位值制
2017-06-23张新春
文︳张新春
非十进位值制
文︳张新春

选择十进制,显然与人类长有10个手指头有关。这一点亚里士多德早就注意到了。在《问题集》XV卷里,亚里士多德给出了人类采用十进制的各种可能的解释。其中有的与毕达哥拉斯有关,毕氏学派认为10是一个完美的数,并给它披上神秘的外衣。首先,10是最小的4种类型的数之和:1+2+3+4=10,其中1非素数也非合数,2是偶素数,3是奇素数,4是合数。另一种解释是1代表点,2代表线(两点确定一条直线),3代表面,4代表体……。最后,亚里士多德指出:是否因为每个人都有10个手指?事实上,前面几种解释都难以站住脚。
其实,在位值制记数法中,以哪个数为基并不是本质问题。因此,除了十进位值制记数法外,还有非十进位值制记数法。
以下一段摘自丹齐克的《数,科学的语言》(上海教育出版社)。
设想:要是人类没有屈伸自如的手指,而只有两只“不分关节”的秃拳,整个文化史会成个什么样子?这是一个有趣的问题。在这种情形之下,假如最终也发展出某种记数法的话,它很可能是二进制的。
人类采用十进制即是一种生理上的凑巧。如果相信从一切事物里都可以看出上帝的匠心,就不得不承认上帝是一位蹩脚的数学家。因为十进制的基底除了生理上的优点外,本身没有多少可以称道之处。几乎一切其他的基底,除了9以外,都和它一样高明,也许还强一些。
老实说,如果让一群专家来选择基底的话,我们也许会看到实用家和数学家之间的争论。实用家坚持要用有最多因数的数,如12为基底;而数学家则要用质数,如7或11为基底。事实上,18世纪后期的大博物学家布封曾经提议举世公用十二进制。他指出:12有4个除数,而10只有2个。他坚持说,正是由于我们的十进制,世世代代以来,人们都感到极为不便,所以虽然10是举世公用的基底,而在大多数的度量衡中,都有以12为基底的辅助单位。
另一方面,大数学家拉格朗日宣称:用质数作基底有绝对的好处。他指出:用了质数基底,每个整分数就都不能化简,因此表示该数的方法就只有一种。在我们现在的命位记数法中,譬如0.36,代表着许许多多个分数:这种暧昧不明之处就大大减少了。
不管我们委托选择基底的贤人们决定采用质数还是合数作基底,我们敢肯定,10甚至是根本不会被考虑的,因为它既非质数,又不含足够多的因数。
在非十进位值制中,最有特点的应该是二进制。相对于十进制需要用10个数码来说,二进制需要的数码少得多,只需0和1两个。比如,十进制的6用二进制表示就是1102,其中的下标2即表明这个数是二进制,从而区别于十进制的110。最高位上的1表示为1个22,即1个4(若按十进制的说法,应该把这个数位叫“四位”)。而右起第二位(应该叫“二位”)上的1表示为1个21。右起第一位(还叫“个位”)的记数单位为20。一般地,任意一个大于0的自然数N都可以表示为:
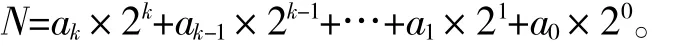
其中,a0,a1,a2,…,ak∈{0,1}且ak≠0并简记为下标2表示为二进制。
除了使用符号少外,二进制的计算法则也非常简单。二进制的加法,就是“0+0=0,0+1=1,1+0=1,1+1=10”这四条规则。我们可以把这几条规则列成一个表:
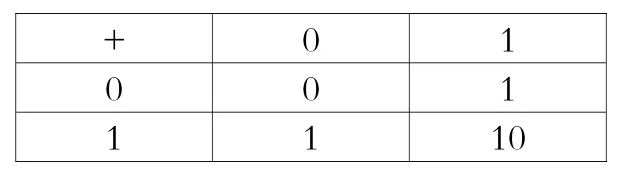
+ 0 1 0 0 1 1 1 10
在此,我们不妨考虑一下,对于十进制的加法而言,类似的表应该是什么样的。这四条规则还可以简化为“0与任何数相加得这个数本身”和“1+1=10”。相对于十进制的九九表,二进制乘法表可以说是一一表,因为只有一句“一一得一”。有了这一条,再加上“0与任何数相乘得0”以及我们熟悉的乘法运算律,就可以进行任意两数的乘法运算了。比如,计算5×6,用二进制计算的过程如右图所示。
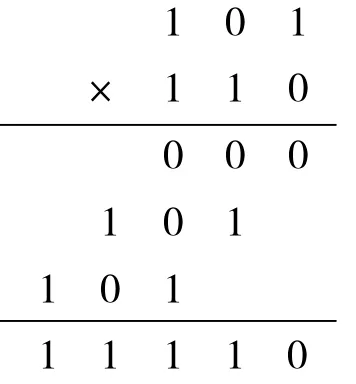
这里确实只用了“一一得一”这一句口诀。
正因为使用符号少,运算规则简单,二进制记数法在计算机中普遍使用。使用二进制必须付出的一个代价是:一个数写出来很长!比如,一千零九十三,用十进制记为1093,而用二进制则要记成10001000101。人类愿意在小时候多学几个符号,多记几句口诀,也不愿意把数写得这么长。而计算机则恰好相反:一个符号就需要用一种物理状态表示,找到10种稳定的物理状态毕竟太难,而有两种稳定状态的东西就多了,比如开关的断开与闭合、电位的高与低、晶体管的导通与截止等,都可分别用0与1表示。简单的计算规则对计算机来说也是非常重要的。而计算机恰恰不在乎多用几个位置记录一个数,于是数被记成很长对它来说影响不大。

从而有:105=11010012。
二进制数与伟大的莱布尼茨密切相关。莱布尼茨是与牛顿分享微积分发明权的数学家。与牛顿不同的是,他是一位“样样皆通的大师”,“可以说莱布尼茨不止活了一生,而是活了好几世。他作为一个外交官、历史学家、哲学家和数学家,在每一个领域中都完成了足够普通人干一辈子的事情”。([美]E·T·贝尔,数学大师,上海科技教育出版社,2004)用拉普拉斯的话来说,“莱布尼茨在他的二进位算术中看到了宇宙创始的形象。他想象1代表上帝,而0代表虚无,上帝从虚无中创造出所有的实物,恰如在他的数学系统中用1和0表示了所有的数”。
数学教育的真功夫是对数学与数学教育的把握,唯此才能成就好的数学课堂。湖南数学教师的老朋友,《湖南教育》的申建春老师开通了微信公众号“与数学老师谈心”,请关注。

