数字化独立单元驱动精梳机机架系统结构的优化设计

王 磊, 蔡 军, 袁 涛, 王生泽

(东华大学 a.机械工程学院; b.纺织装备教育部工程研究中心, 上海 201620)

数字化独立单元驱动精梳机机架系统结构的优化设计

王 磊a, b, 蔡 军a, 袁 涛a, 王生泽a, b

(东华大学 a.机械工程学院; b.纺织装备教育部工程研究中心, 上海 201620)

基于数字化独立单元驱动精梳机机架的低阶固有频率及结构质量对其设计参数灵敏度分析的结果, 选取其中较高灵敏度设计参数为优化设计变量, 以机架结构质量最轻为目标, 同时考虑满足前几阶低阶固有频率避开周期激励基频与倍频的性能要求, 建立机架的ANSYS APDL参数化有限元模型, 对机架系统结构进行优化设计, 得以在轻量化下使机架系统具有较高的动态承载能力.该优化设计方法可有效减少机架系统有限元模型优化设计的规模, 提高优化分析计算的效率, 进而对推进较大型复杂结构有限元模型的动态性能优化设计具有借鉴作用.

参数化有限元模型; 低阶固有频率; 灵敏度分析; 设计参数; 优化设计

数字化独立单元驱动精梳机是一种新型的精梳机, 其锡林轴、钳板轴、分离罗拉、引出罗拉等分别为独立电机驱动, 使得精梳机的传动机构大大简化, 不仅方便设计和维修, 更重要的是各个工作部件的工艺运动参数可以独立调节, 可极大地提高精梳机的适纺性能, 并有利于精梳棉条质量的提高[1].

数字化独立单元驱动精梳机机架系统承受着来自于钳板机构、锡林机构和分离罗拉机构等的(支承动反力)动态载荷作用, 其动态承载能力的提高及轻量化的优化设计具有重要工程价值.

传统精梳机一般具有八眼, 因此, 数字化独立驱动单元精梳机按眼数可分为单眼驱动单元(8个)、双眼驱动单元(4个)、四眼驱动单元(2个)或八眼驱动单元(1个)等.本文以单眼独立单元驱动精梳机机架为研究对象, 在ANSYS软件环境下建立机架系统的有限元模型, 基于其低阶固有频率、结构质量对设计参数的灵敏度分析(sensitivity analysis, 简称SA)结果, 选取机架系统灵敏度较高的主要设计参数作为结构优化的设计变量, 可有效减少机架系统有限元模型优化设计规模、提高优化计算效率、改善机架结构的动态承载性能.

1 机架系统的有限元模型

本文采用ANSYS软件建立单眼独立单元驱动精梳机机架系统有限元模型, 并对其进行优化分析.在建模过程中对机架系统做了一定的简化: 忽略对结构影响不大的螺栓孔、小孔; 略去半径小于5 mm的倒角.通过选择合适的有限元单元, 对简化后建立的有限元模型结构进行网格划分, 单元数为650 237个.墙板结构材料为铸铁, 其材料属性: 弹性模量为66 178 MPa, 泊松比为0.27, 质量密度为7 200 kg/m3.连接板AB、连接板C、连接轴、锡林轴、钳板轴、分离罗拉轴、喂转罗拉轴和台面压辊轴材料为普通碳钢, 其材料属性: 弹性模量为210 000 MPa, 泊松比为0.28, 质量密度为7 800 kg/m3.单眼独立驱动机架结构如图1所示, 相关结构参数及名称如表1所示.

图1 单眼独立单元驱动机架结构示意图Fig.1 Independent-unit driven structural diagram of a group frame

表1 机架结构参数名称及说明

2 机架结构低阶固有频率灵敏度分析

2.1 固有频率对设计参数的灵敏度分析

设{ui}为特征值λi对应的正则振型, 则结构有限元动力分析的特征方程为

([K]-λi[M]){ui}=0

(1)

将式(1)对设计参数xj求偏导可得

([K]-λi[M]){ui, j}′=0

(2)

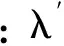
用{ui}T左乘式(2), 并由特征方程(1)两边转置且注意质量与刚度矩阵的对称性可知{ui}T([K]-λi[M])=0, 则有

由于{ui}为正则振型, 即

可得特征值对设计参数xj的灵敏度式[2-5]为

(2)

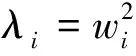
(3)

考虑到在实际计算中, 结构的质量矩阵和刚度矩阵很难表示为设计参数的显函数, 因此, 通常将设计参数通过摄动Δxj, 得到质量矩阵和刚度矩阵的变化[ΔjM]和[ΔjK], 由此可得结构固有频率对设计参数xj的灵敏度的数值计算式为

(4)

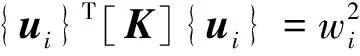
(5)

式中: [M, j]、[K, j]为单一设计参数xj摄动后的结构系统质量矩阵和刚度矩阵.

2.2 低阶固有频率对机架结构参数的灵敏度分析

考虑到本文所研究精梳机的工作速度最高为500钳次/min, 即相当于机架支承系统承受的周期激励的基频(f0=ω0/2π)为8.33 Hz, 并且由精梳机周期激励力的幅频特性可知, 激励的前二倍频起主导作用, 即可取它2倍频作为所关注的外部激励频率参考.工程上, 常以不大于所关注外部激励频率5～10倍数值作为截取所分析机架结构前几阶低阶模态的依据.由此, 本文取所关注外部激励频率5倍(即10倍外部激励基频频率)来分析, 从而确定本文机架结构的主要动态特性可仅考虑取其前三阶低阶固有频率(21.893, 58.301, 84.278 Hz,fi=ωi/2π,i=1, 2, 3)来衡量.

选取机架结构相关设计参数如表1所示, 进行前三阶低阶固有频率对结构参数的灵敏度分析(结构设计参数摄动量取1%).采用ANSYS软件对机架结构模型进行灵敏度分析, 结构前三阶低阶固有频率灵敏度经Min-Max标准化后的低阶固有频率灵敏度标准化数值与参量的关系如图2所示.

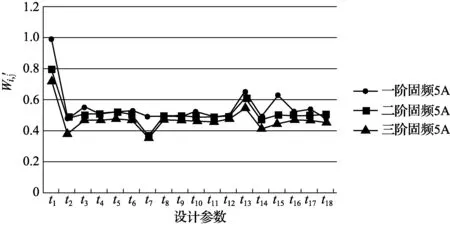
图2 低阶固有频率对设计参数的灵敏度Fig.2 Sensitivity of low-order natural frequency to design parameter

由图2可知, 参数t1、t13、t15变化对前三阶固有频率影响相对更显著.

3 机架结构质量对结构参数灵敏度 分析

机架结构质量对结构参数灵敏度是指结构质量对设计参数的改变的变化率(结构设计参数摄动量取1%).利用一阶差商灵敏度计算式求解, 结果如图3所示.

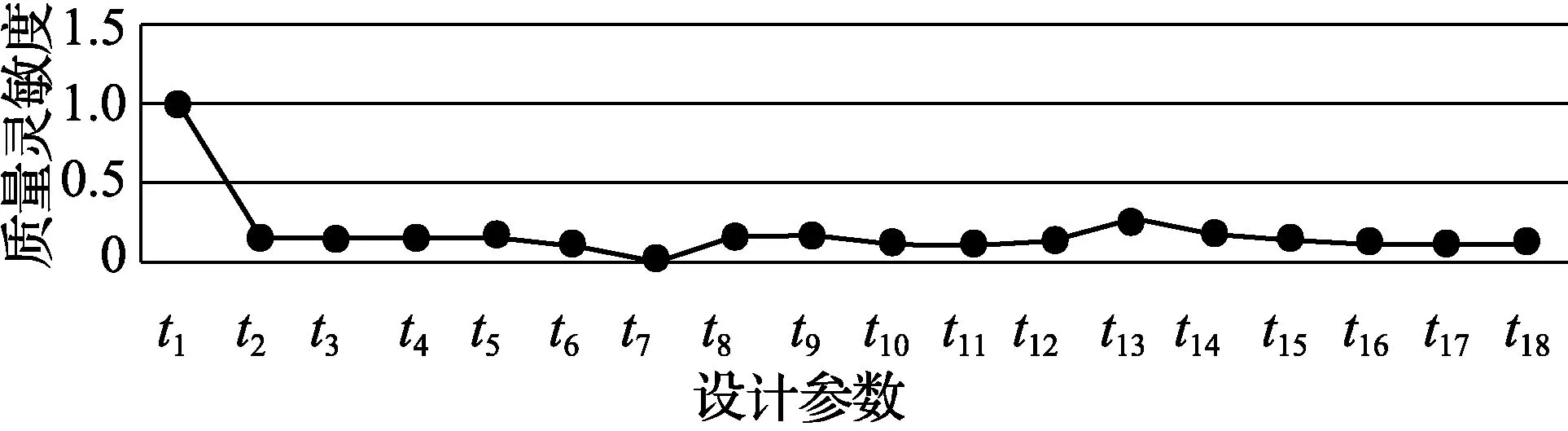
图3 结构质量对设计参数灵敏度Fig.3 Sensitivity of frame mass to design parameter

由图3可知, 机架结构质量对结构参数灵敏度较大的参数是t1和t13.这表明相较于其他参数, 当结构参数t1和t13变化时引起的精梳机机架质量变化更加显著.

4 基于灵敏度分析的机架系统结 构优化设计

通过以上灵敏度分析, 综合考虑对机架结构前三阶低阶固有频率和结构质量影响较大的结构参数, 选取t1、t13和t15作为机架结构优化的设计变量.针对这些优化设计变量, 利用ANSYS软件提供的ADPL参数化语言建立结构的参数优化模型.优化数学模型目标函数如下

f(t1,t13,t15)=min(m)其中:m为机架系统结构的质量.

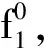
通过优化计算, 设计变量值(圆整)t1=46 mm,t13=105 mm,t15=52 mm. 相应参量优化前后结果对比如表2所示.

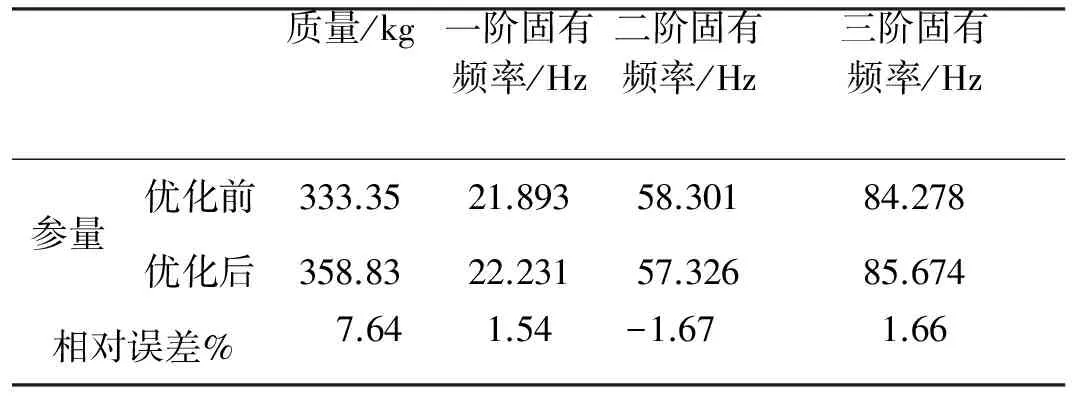
表2 优化前后结果对比

由表2可知, 经过优化求解后机架系统的第一、三阶低阶固有频率均增大, 第二阶固有频率略减小.优化前机架结构a1=0.63,a2=0.99,a3=0.11, 其二、三阶固有频率与外周期激励载荷的相关倍频频率较接近, 容易引起机架结构大的振动; 优化后机架结构a1=0.67,a2=0.87,a3=0.28, 其前三阶低阶固有频率都较好地避开了外周期激励载荷的倍频频率, 改善了机架系统动态承载性能, 并且机架系统结构的质量仅略有增加, 这对于动态承载性能改善的程度而言是可接受的.

5 结 论

(1) 通过参数的低阶固有频率灵敏度和质量灵敏度分析, 选取对低阶固有频率和结构质量影响较大的结构参数作为优化设计变量, 可有效减少优化设计规模、提高机架系统有限元模型的优化效率.该优化设计变量的选取方法可为结构优化设计的高效性提供参考.

(2) 考虑多阶低阶动态性能约束条件, 建立机架的ANSYS APDL参数化有限元模型, 对机架系统进行优化设计.相较于原始设计, 优化后的机架结构多阶低阶固有频率均有效地避开了激励载荷主要倍频频率, 改善了机架系统的动态承载性能.

[1] 王生泽, 顾洪波, 何勇, 等.数字化独立单元驱动精梳机: 200810208037.8[P]. 2011-04-27.

[2] 林家浩.结构动力优化中的灵敏度分析[J].振动与冲击.1985, 4(1): 1-6.

[3] 钱袁萍, 唐勰, 何国平, 等.基于ANSYS的PYQ202C平压压痕切线机机座的动态灵敏度分析[J].机械设计与研究, 2003, 19(6): 70-72.

[4] 李志祥, 王军杰, 吴德宏.边梁式车架的结构灵敏度分析及设计优化[J].机械设计与制造, 2010, 3(3): 48-50.

[5] 杨英, 赵广耀, 孟凡亮.某轿车白车身结构灵敏度分析及优化设计[J].东北大学学报(自然科学版), 2008, 29(8): 1159-1162.

[6] 何力.船舶板架结构动力优化设计方法研究[D].武汉: 华中科技大学船舶与海洋工程学院, 2011.

[7] 王从晶.全船结构动力特性的优化设计研究[D].上海: 上海交通大学船舶海洋与建筑工程学院, 2011.

[8] 林家浩.有频率禁区的结构优化设计[J].大连工学院学报, 1981, 20(1): 27-37.

(责任编辑：刘园园)

Optimization Design of the Frame Structure for Digital Independent-Unit Driven Comber

WANGLeia, b,CAIJuna,YUANTaoa,WANGShengzea, b

(a. College of Mechanical Engineering; b. Engineering Research Center of Advanced Textile Machinery,Ministry of Education, Donghua University, Shanghai 201620, China)

The design parameters with higher sensitivity relatively were choosen as the design variables of optimization based on the analytic results of sensitivity of the low-order natural frequency and structural mass of digital independent-unit driven to design parameters, and the goal to minimize the weight of the frame was set. Then, in order to sustain a higher dynamical load-bearing properties with a lightweight frame, the ANSYS ADPL parameterized finite element model was established to optimize and design the frame structure. The optimal model meets the requirement that the first few orders of natural frequencies do not coincide with the periodic and multiplier excitation fundamental frequency. The optimization design method has the advantages of reducing the scale of optimal design of the finite model of frame system and improving the efficiency of optimal analysis. It also provides a referential approach for the optimal design of the dynamic performance of large-scale complex frame system.

parametric finite element model; low-order natural frequency; sensitivity analysis; design parameter; optimization design

1671-0444 (2017)02-0251-04

2016-01-15

王 磊(1988—)，男，湖南常德人，硕士研究生，研究方向为现代设计理论方法及应用. E-mail: m18317132163@163.com 王生泽(联系人)，男，教授，E-mail: wasz@dhu.edu.cn

TH 122; TS 122.2

A