基于分形理论的混联机器人构型设计方法

2017-06-19葛姝翌1b2a2b丁泽华朱景原

东华大学学报（自然科学版） 2017年2期

葛姝翌, 曹毅, 1b, 2a, 2b, 丁泽华, 周睿, 朱景原

( 1. 江南大学a. 机械工程学院; b. 江苏省食品先进制造装备技术重点实验室, 江苏无锡 214122; 2. 上海交通大学a. 机械系统与振动国家重点实验室; b.系统控制与信息处理教育部重点实验室, 上海 200240)

基于分形理论的混联机器人构型设计方法

葛姝翌1a, 曹毅1a, 1b, 2a, 2b, 丁泽华1a, 周睿1a, 朱景原1a

为综合得到混联机器人构型, 基于分形理论提出了一种新的混联机器人机构构型设计方法, 其能够有效地解决多路径横向非典型混联机构构型的设计问题.首先, 阐述了机构拓扑图和分形理论的概念; 其次，建立了运动副及其空间方位关系的二进制码, 规定了为求解机构拓扑图的路径法则和用以推导运动副的输出位移子集的串并联计算法则; 然后，根据分形理论推导出分形后的机构拓扑图, 并适配运动副从而获得混联机器人机构的整体构型; 最后，根据该构型设计方法, 实现了2T1R三自由度混联机构的构型设计, 并对综合后的混联机器人机构进行分析, 验证了该构型设计方法的可行性.

混联机器人构型; 机构拓扑图; 分形理论; 路径法则; 二进制代码

混联机器人概念的提出, 引发了机器人构型的新潮流, 并得到了国内外研究者的广泛关注.文献[1]提出了基于自由度公式的欧氏运动平台混联机构的综合.文献[2]根据Assur杆组的组合形式, 对其进行构型的分割与组合, 从而得到不同形式的基于链群的混联机构.文献[3-4]的研究将两个Stewart并联机构进行串联, 得到串并混联的机构.文献[5]则将多个并联机构单元进行串联组合, 得到具有柔顺灵巧运动的混联结构.文献[6]将两个并联机构进行串联, 并将两级动平台输出的双末端操作器进行分析后得到相对运动的输出.在国内, 文献[7]提出了基于李群理论得到三自由度RPR等价并联机构构型综合, 文献[8-9]提出了基于方位特征集和自由度分配的混联机构构型设计方法.文献[10]基于李群理论得到混联支链在不同构型下运动的群论表达式.相关的混联机构构型综合还包括其他不同的串并联组合形式[11-15].现如今, 混联机构的发展不仅仅停留在理论知识的延伸上, 制造业已实现了混联机器人的生产及应用.例如瑞典Neos Robotic公司生产的5自由度Tricept系列机器人、德国DS-Technology公司生产的5自由度Exechon机器人、Adept Technology公司生产的Adept Quattro机器人、天津大学黄田发明的TriVariant系列机器[16-20].

综上所述, 不难发现上述混联机器人机构可划分为3种形式[21]: (1)并联机构通过其他机构串联而成; (2)并联机构直接串联在一起; (3)在并联机构的支链中采用不同的结构.混联机器人机构的型综合主要关注于支链的设计方法, 其支链的布局较为单一.故上述理论一般不适用于具有多路径横向非典型性的混联机构的构型设计.机构拓扑创新是机械发明最具挑战性的核心内容, 因此混联机器人机构尤其是具有多路径横向非典型性的混联机器人机构构型设计方法的研究, 不仅具有重要的理论意义, 还具有广泛的应用前景.

为有效地解决多路径横向非典型混联机器人机构的构型设计问题, 本文提出基于分形理论的混联机器人机构构型设计方法.首先对机构拓扑图和分形理论的概念进行阐述, 同时建立运动副及其空间方位关系的二进制代码结构, 并规定了应用于分析计算的路径法则和串并联计算法则, 之后对分形理论推导出的机构拓扑图适配运动副, 最终获得混联机构的整体构型.

1 分形理论和机构拓扑图

1.1 分形理论的基本概念

自B.Mandelbrot提出分形几何理论[22]至今, 该理论已经成为了一门独立的学科, 并逐渐渗透到自然科学、社会科学及工程技术中, 机械工程领域也不例外.

分形集合一般具有如下特征[23]: (1)自相似性; (2)精细的结构, 即包含有任意小比例的细节; (3)极不规则, 它的整体和局部不能用传统的几何语言来描述; (4)由迭代得到; (5)大多数情况下, 以某种方式定义的分形集合的分形维数大于它的拓扑维数.

分形理论的一个特点就是要利用分形维度的视角和数学方法描述客观事物, 与一维、二维、三维甚至四维空间的描述相比, 它的真实性和直观性都更为优秀.分形理论的这一特点特别适合应用在机械工程领域, 其不但可以直观地展现机械特性, 还可以降低工程难度和提高工程效率.

1.2 机构拓扑图

机构拓扑图由静平台、动平台和支链构成.其中, 静平台是机架, 动平台是机构末端输出平台.支链的具体定义为由连接末端动平台、静平台和中间过渡平台的支链按照一定方式组合而成, 并通过一定的连接关系形成路径.路径的位置关系是始于静平台, 终于动平台, 其只与静平台和动平台有关系.

图1 机构拓扑图分形方式Fig.1 Fractal form of the topological graph

机构的拓扑设计是混联机构构型设计的理论基础, 其主要思想是将混联机构抽象为连杆机构, 首先研究机构的拓扑结构, 其次对支链和路径进行结构设计, 从而得到混联机器人机构的构型.为快速有效地生成不同机构拓扑图, 将分形理论运用到机构拓扑图中, 其能够产生3种分形方式: 链分形、平台分形、链台分形[24-26], 如图1所示.

1.3 分形方式的具体分析

1.3.1 链分形的定义

通过运动副连接两个平台, 则称该运动副的组合为支链.一级支链, 即只连接两相邻平台, 无任何跨越平台行为的支链.二级支链, 连接的两平台中间需相隔一过渡平台.多级支链以此类推.

链分形是对一级支链进行的分形(如图1中Ⅰ所示), 其可以细分为纵向链分形和横向链分形, 其中横向链分形需要的条件较为苛刻, 需要存在至少4个平台(包括动、静平台), 且含有2个过渡平台为横向平行关系.

1.3.2 平台分形的定义

平台分形即把已存在的支链打开, 加入新的过渡平台, 再连接新平台两端的支链(如图1中Ⅱ所示), 值得注意的是，拓扑机构只能在已有支链的位置进行平台分形.

1.3.3 链台分形的定义

链台分形是指在任意平台上分形出一个支链和一个平台分形方式, 且新生成的平台为独立输出, 不与机构的输出动平台有任何联动关系, 即得到多输出动平台的拓扑机构(如图1中Ⅲ所示).

必须指出的是: 链分形和平台分形输出的拓扑结构为闭环拓扑结构, 即输出平台有且仅有一个; 而链台分形输出的是开环拓扑结构, 即输出动平台不止一个, 适用于多点工作平台环境.本文主要考虑内容为闭环拓扑结构, 故链台分形在本文未予考虑.

由于分形总次数不受限制, 因此有必要建立分形与支链的关系模型, 具体如式(1)所示.

(1)

式中:Fdof为机构自由度数;Ri为第i个路径上的驱动运动副数(i=1, 2, … ,n);N为分形次数;b为被动支链数;m为主动支链数;L为链分形次数;P为平台分形次数;Pmin为最短支链的平台分形次数.

1.4 分形与机构拓扑图的关系

支链作为机构拓扑图的重要组成部分, 也是分形过程中最重要的组成环节.支链和分形存在密不可分的关系, 如图2所示.

图2 分形与支链的关系Fig.2 Relationship between fractal and branches

链分形需按照其分类各自进行分析, 即纵向链分形和横向链分形, 其中横向链分形的情况比较特殊, 其主体是横向支链, 指用于横向连接两平行的中间过渡动平台之间的支链.经过横向链分形的拓扑机构图就能够生成多路径横向非典型的混联机构.链分形对支链和路径的影响关系如图3所示.

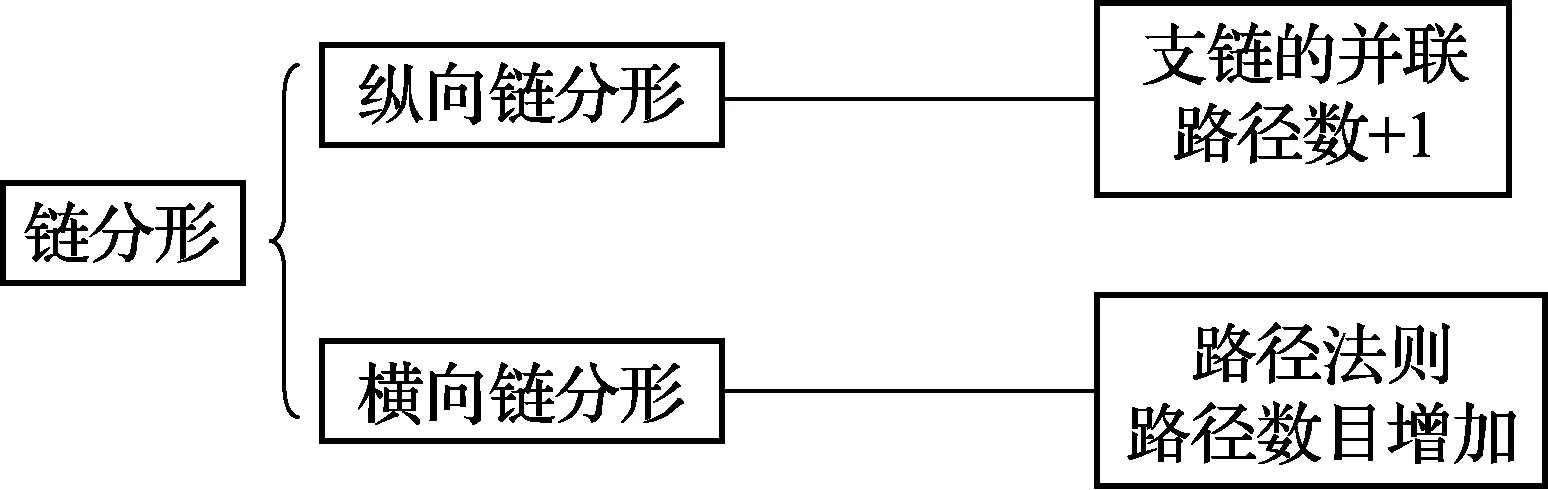
图3 链分形与支链的关系Fig.3 Relationship between branch fractal and branches

2 运动副的表达及运算法则

2.1 运动副的描述

从机构拓扑图到混联机构构型的转变, 需要经历机构拓扑图生成拓扑路径, 由拓扑路径定义机构支链, 再由支链适配具有给定末端输出特征的运动副.因此, 运动副的描述是混联机构设计的重要基石, 其可划分为两方面: 一是运动副的表达方式, 二是运动副轴线间方位关系的表达方式.

为使运动副的表达更加简洁明了, 本文提出了8位二进制代码的表达方式, 其能清楚地阐述运动副的种类、运动副与基坐标轴的位置关系、相邻运动副轴线的方位关系及平台和支链间的连接关系.值得指出的是, 二进制代码的表达方式还有利于后续的数字化设计.

2.1.1 单一运动副的表达形式

单一运动副可由5位二进制码表示, 具体如表1所示.

表1 单一运动副二进制表示方法

单一运动副可细分为6种情况, 如图4所示.

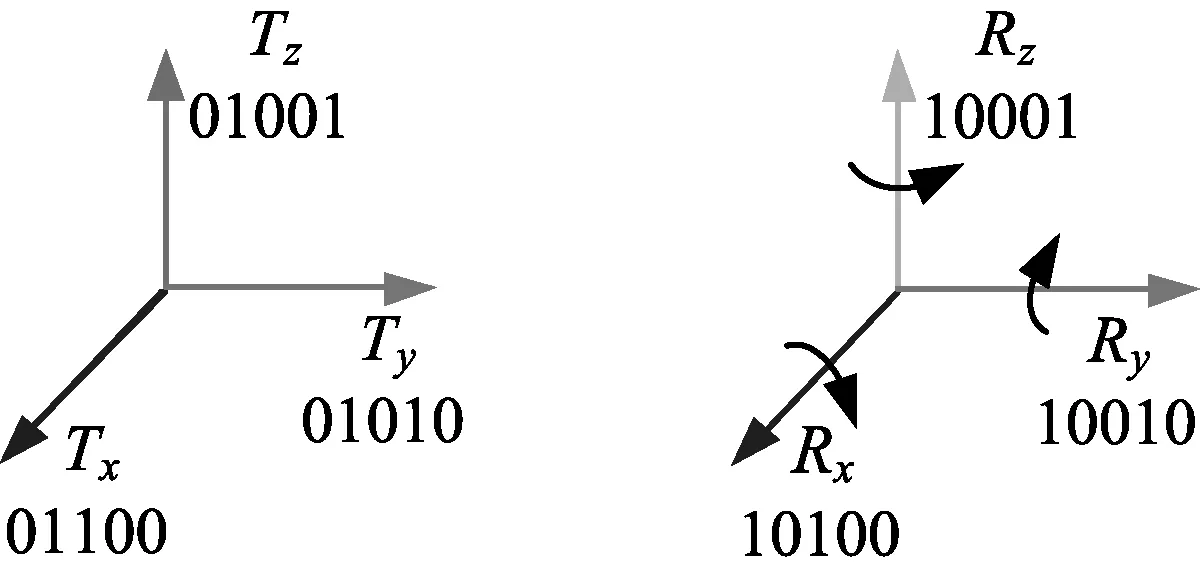
图4 运动副的描述

表1可划分为前后两部分, 表征不同的含义:

(1) P0.4和P0.3为运动副类别位R、T.若P0.3=1, 则表示运动副为移动副; 若P0.4=1, 则表示运动副为转动副.P0.3和P0.4不能同时为1.

(2) P0.2、P0.1和P0.0为运动副轴线方向位x、y、z, 此方向位的矢量方向与基坐标轴方向一致.若P0.0=1, 则表示运动副的轴线与基坐标轴的z轴平行; 若P0.1=1, 则表示运动副的轴线与基坐标轴的y轴平行; 若P0.2=1, 则表示运动副的轴线与基坐标轴的x轴平行.方向位x、y、z最多只能有一位为1.

方向位同时还可以表示与邻近运动副的关系.当两邻近运动副的某一方向位均为1时, 则表示两运动副的轴线平行或者同轴; 若两邻近运动副的不同方向位均为1, 则表示两运动副的轴线垂直.

2.1.2 相邻运动副间轴线的方位关系

由于单一运动副中的方向位只能表示相邻运动副间轴线的同轴、平行和垂直3种方位关系, 且不能区别同轴和平行.为全面表征各运动副之间的方位关系, 需补充3位二进制码进一步描述相邻运动副间的方位关系, 如表2所示.

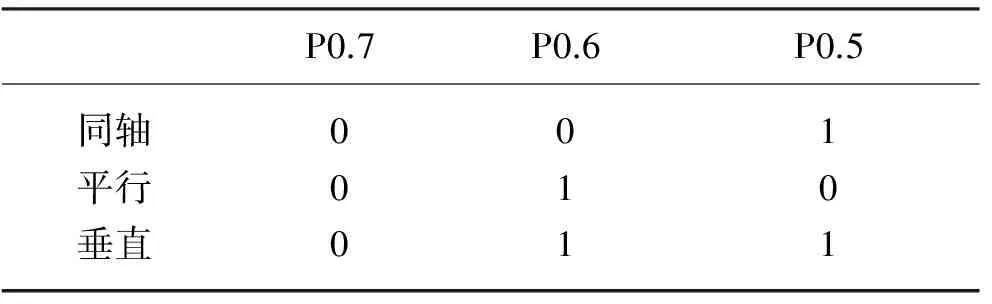
表2 相邻运动副方位关系的表达方法

(续表)

其中, 若相邻运动副轴线的方位关系是轴线成角度, 那么两运动副轴线必相交于一点.

值得指出的是，大多数方位关系都具有传递性, 例如平行、同轴等.具有传递性的方位关系为正则方位关系, 其余为非正则关系[27].

2.2 运算法则

2.2.1 串并联计算法则

适配运动副的过程就是已知支链输出位移子集对运动副进行定义和二进制码求交、求并运算的过程.运动副的串联就是不同的二进制数组进行求并集的过程; 支链的并联就是不同的二进制数组进行求交集的过程.

故而, 定义串联运算符号为#, 并联运算符号为&.由于运动副方位关系中存在非正则关系, 故在计算中不再引入方位关系, 只保留xyz的方位表达.

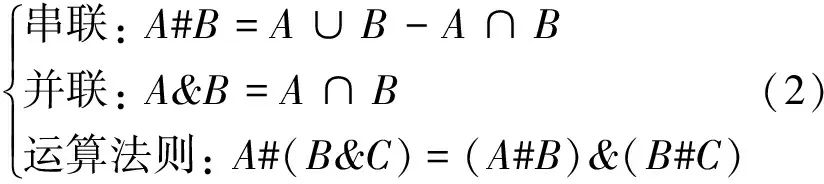
式中: A和B为输出位移子集; ∪为求并运算符; ∩为求交运算符.

举例说明, 当一个轴线平行于x轴的圆柱副和一个轴线平行于x轴的平面副串联, 由式(2)可求末端输出的位移子集为

C(x)#G(x)=[R(N, x)·T(N, x)]#[R(N1, x)·T(z)·T(y)]=

式中:C(x)为圆柱副, 其具有沿x轴的移动和绕x轴的转动;G(x)为平面副, 其具有在yz平面内具有沿y轴和z轴的移动以及绕x轴的转动.

2.2.2 路径法则

路径法则是基于机构拓扑图, 对于给定的机构动平台末端输出位移子集, 找出所有满足条件的路径及其支链配置.其中, 每条路径所含支链间的关系定义为串联关系, 各路径之间定义为并联关系.通过此定义即可将动平台的输出位移子集转化为各支链交集和并集的计算结果, 如式(3)所示.

(3)

式中:Bij为第j条路径的第i个支链末端输出位移子集;Rj表示路径输出位移子集;P为机构末端动平台输出位移子集;I为第j条路径的支链总数;J为路径总数.当存在横向支链时, 不同路径会存在共用同一支链的现象.

举例说明路径法则, 如图5所示.

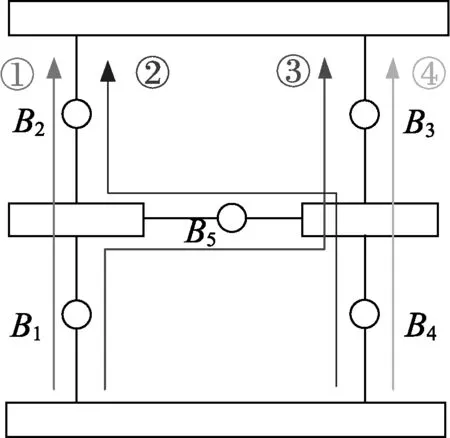
图5 路径法则示意Fig.5 An example of a route rule

由图5可知, 从静平台到动平台一共有4条路径, 分别是B1B2、B1B5B3、B3B4、B4B5B2, 由式(3)可推导出其运动输出为

P=(B1#B2)&(B1#B3#B5)&(B3#B4)&(B4#B5#B2)

3 混联构型设计方案

3.1 混联构型设计依据

混联机器人的构型设计是基于与机构拓扑结构适配相应的运动副, 并判定适配运动副的布局是否符合设计过程.基于分形类别, 混联机器人机构被分成两类: 第一类机构拓扑图具有横向支链, 且可能后续分形得到三维分形混联机构(如图6(a)所示); 第二类机构拓扑图不具备横向支链的特征, 即不存在横向链分形的可能(如图6(b)所示).

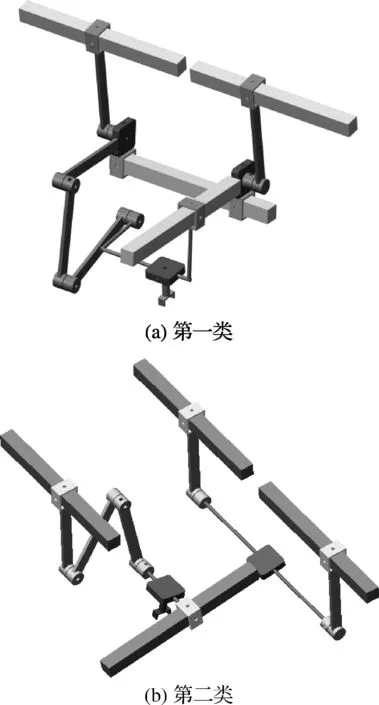
图6 混联机器人机构Fig.6 Hybrid robot mechanisms

3.2 混联构型设计原则

基于2.2节研究表明, 对于给定的末端动平台输出位移子集P, 由式(3)可分别推导出路径输出位移子集Rj和支链末端输出位移子集Bij, 从而实现给定末端输出位移子集的混联机器人构型设计.为简化有多路径横向非典型性的混联机器人机构构型设计, 本文选定最短路径, 即混联机器人的末端动平台输出位移子集与所选最短支链的输出位移子集一致, 因此, 最短路径上的每个元素皆为驱动运动副, 其余的运动副可为被动运动副.

基于最短路径, 混联机器人机构的构型设计原则可以表示为:

(1) 若仅进行链分形, 则所得的机构拓扑图为多支链并联机构, 若要实现混联机器人机构构型设计, 其适配的运动副需存在串联运动副的形式, 或者选择串联构型替代并联支链;

(2) 若仅进行平台分形, 则所得机构拓扑图为多平台串联机构, 若要实现混联机器人机构构型设计, 其适配的运动副需存在并联运动副的形式, 或者选择并联构型替代串联支链;

(3) 对于含有横向支链的机构拓扑图, 与最短路径中的支链处于对称或者平行位置的支链, 其输出位移子集必须是对应最短路径中的支链输出位移子集的父集或者其本身.

3.3 混联构型的设计方法

根据上述设计原则及理论依据, 混联机器人构型设计步骤如下:

(1) 绘制最简机构拓扑图.基于最简机构拓扑图, 依据混联构型设计原则生成构型拓扑图; 对于给定的构型拓扑图, 依据式(3)路径法则推导其拓扑路径.

(2) 基于步骤(1)中的路径, 采用Matlab编程的方式获得满足条件的支链, 选取支链并适配运动副, 完成设计过程.

(3) 依照式(2)计算各个支链B1-Bm(m为支链总数)的输出位移子集, 再将结果代入到步骤(1)中的各路径计算式中, 获得各路径输出位移子集.

(4) 已知路径间为并联关系, 可推导出末端动平台输出位移子集, 并与预期的末端输出位移子集比较, 若一致, 则表明结果已核实, 完成证明过程.

为了更加清楚地表达具体设计步骤, 用流程图来反映设计流程, 如图7所示.

图7 混联机器人设计流程图Fig.7 A design flowchart of hybrid robot

4 2T1R三自由度混联机器人型综合

4.1 混联构型综合

为验证上述混联机器人机构构型设计方法的有效性, 根据该方法的设计步骤, 设计一种末端动平台输出为2T1R的混联机器人.

首先对最简机构拓扑图进行分形, 可分为两种情况: 平台分形和链分形, 如图8所示.以图8中平台分形为例, 经多次分形后获得多种机构拓扑图, 如图9所示.

图8 机构拓扑图初次分形Fig.8 First fractal of topological graph

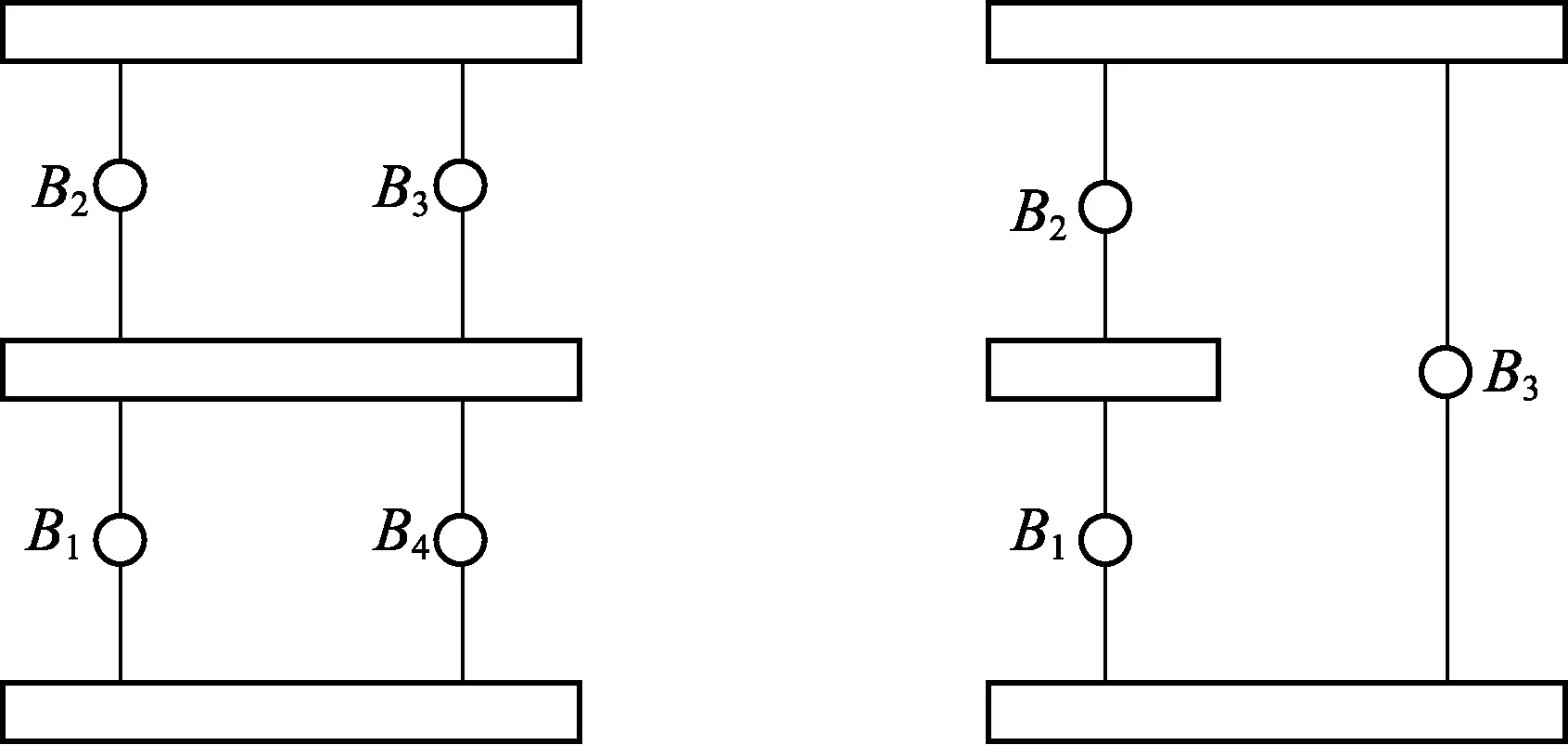
(a) P-L1-L2 (b) P-L0

基于式(3), 图9所示机构拓扑图对应的动平台末端输出位移子集为:

(1) (B1#B2)& (B1#B3)&(B2#B4)& (B4#B3);

(2) (B1#B2)&B3;

(3) (B1#B2)& (B3#B4);

(4) (B1#B2)& (B1#B3#B5)& (B3#B4)& (B4#B5#B2).

不失一般性, 进一步以图9(d)所示的机构拓扑图为例, 假设B1B2为最短路径2T1R, 为保证给定的机构动平台末端输出特征, 因此, 其余各路径的最终输出位移子集必为2T1R的父集或其本身, 且符合设计原则.

为实现基于图9(d)所示的机构拓扑图的构型设计, 必须确定: (1)除最短路径外其余路径的输出位移子集; (2)符合路径输出位移子集的各支链的输出位移子集.其中, (1)的Matlab求解程序伪代码如下:

1 由父集可得路径各自由度:

2 a={2T1R 2T2R 2T3R 3T1R 3T2R 3T3R}

3 for E=a1: a6

4 for F=a1: a6

5 for G=a1: a6

6 output E, F, G

7 end

8 end

9 end

对于求解后的剩余路径输出位移子集, 设B1B2合成路径为a,B3B4合成路径为E,B1B5B3合成路径为F,B4B5B2合成路径为G, 则要求各支链满足式(4).

(4)

式中:B1B2的位移子集分别为T(U)R(U)和T(V), {E}、{F}、{G}分别为路径E、F、G的输出位移子集.对于给定的输出位移子集{E}、{F}、{G}, 其支链的末端输出位移子集的Matlab求解程序伪代码如下:

1 E=[TXTYTZRXRYRZ];

2 F=[ TXTYTZRXRY];

3 G=[ TXTYTZRXRY];

4 [m, n]=size(intersect(E, G));

5 A1=intersect(E, G);

6 a=length(A1);

7 for i=1: a

8 S=nchoosek(A1, i);

9 [m1, n1]=size(S);

10 for j=1: m1

11 A=S(j, : )

12 B1=setdiff(E, A);

13 u=exp(0.6931*length(A))-1;

14 if u<=1

15 B=B1

16 C1=union(setdiff(G, A), setdiff(F, B));

17 C=C1

18 C=union(A, C)

19 B=[A B1]

20 C1=union(setdiff(G, A), setdiff(F, B));

21 C=C1

22 C=union(A, C)

23 end

24 if u>1

25 B=B1

26 C1=union(setdiff(G, A), setdiff(F, B));

27 C=C1

28 C=union(A, C)

29 for k=1: u

30 T1=nchoosek(A, k);

31 [m2, n2]=size(T1);

32 for l=1: m2

33 T=T1(l, : );

34 B=[B1 T]

35 C1=union(setdiff(G, A), setdiff(F, B));

36 v=exp(0.6931*length(B))-1;

37 if v<=3

38 C=C1

39 C=union(A, C)

40 end

41 if v>3

42 C=C1

43 for p=1: length(A)

44 W1=nchoosek(A, p);

45 [m3, n3]=size(W1);

46 for q=1: m3

47 C2=W1(q, : );

48 C=C1;

49 C=union(C, C2)

50 end

51 end

52 此处为节省空间省略若干end

53 end

其中的一组支链运动副如表3所示, 此处采用李群理论[28-29]对适配运动副进行分析.以B1为例进行说明, T(U)代表移动副T, 沿单位矢量x方向移动; R(U)代表转动副R, 其轴线绕单位矢量x转动.其中U、V、W分别代表单位矢量x、y、z.

根据选择的机构拓扑图和适配的运动副绘制混联机器人构型, 如图10所示.

表3 支链适配运动副

注：U、V、W分别代表单位矢量x、y、z.

图10 2T1R混联机构构型三维图Fig.10 3D model of 2T1R hybrid mechanisms

值得指出的是, 上述求解过程同样适用于图9中(a)、(b)、(c)所示的机构拓扑图的构型综合, 限于篇幅这里不做进一步的阐述.

同时, 需要指出的是, 本文所论述的基于分形理论的混联机构设计方法, 不仅可以用于只包含纵向支链的混联机构的设计, 且还能完成具有横向支链的混联机构的设计, 如图11所示.其中的横向支链设计弥补了其他混联机构设计理论只能纵向延伸的缺点, 拓宽混联机构设计思路, 使得混联机构设计全方位发展.

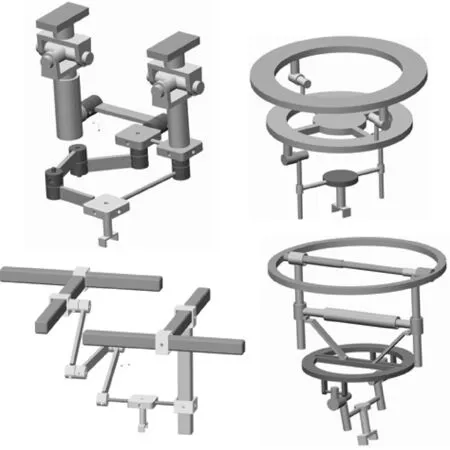
图11 混联机构构型图Fig.11 Configuration of hybrid mechanisms

4.2 运动特征分析

为验证上述构型设计方法的正确性, 以图10所示的混联机构为例进行机构的末端运动特征分析如下.

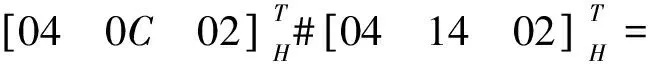
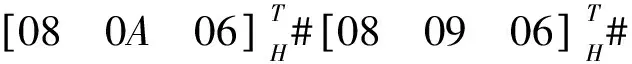
由图9 (d)可知, 从静平台到动平台的路径共有4条, 分别是B1B2,B1B5B3,B4B3,B4B5B2.基于式(2), 可计算各路径的输出位移子集如下:

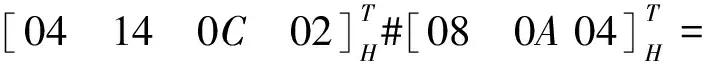
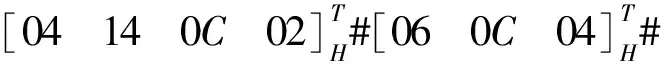
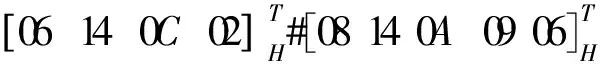
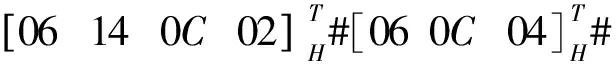
可得最终动平台的输出为

由此表明, 机构动平台末端输出位移子集确实为期望的运动输出位移子集, 核实无误, 从而验证了上述混联机构型设计方法的正确性.

5 结语

本文基于分形理论提出了一种混联机器人构型设计方法, 其能够有效地解决多路径横向非典型混联机构构型的设计问题, 并得到以下结论:

(1) 根据分形理论建立了对拓扑结构图的有序分形, 并通过对运动副的分配及输出位移子集的排列组合, 实现了混联机器人机构构型的多样化;

(2) 所提出的路径法则可用于求解复杂机构拓扑图的多路径输出, 与此同时规定了运动副输出位移子集的串并联计算法则, 并揭示了串并联计算法则与分析方式之间的内在联系;

(3) 实现了2T1R混联机器人机构的构型设计，并验证了本文所提出的混联机构设计方法的正确性.

[1] ALIZADE R, CAN F C, GEZGIN E. Structural synthesis of Euclidean platform robot manipulators with variable general constraints[J]. Mechanism & Machine Theory, 2008, 43(11): 1431-1449.

[2] CAMPOS A, BUDDE C, HESSELBACH J. A type synthesis method for hybrid robot structures[J]. Mechanism & Machine Theory, 2008, 43(8): 984-995.

[3] ROMDHANE L. Design and analysis of a hybrid serial-parallel manipulator[J]. Mechanism & Machine Theory, 1999, 34(7): 1037-1055.

[4] TANEV K T. Kinematics of a hybrid(parallel-serial)robot manipulator[J]. Mechanism & Machine Theory, 2000, 35(9): 1183-1196.

[5] TSAI L W, JOSHI S. Kinematic analysis of 3-DoF position mechanisms for use in hybrid kinematic machines[J]. Journal of Mechanical Design, 2002, 124(2): 245-253.

[6] RAMADAN A, INOUE K, ARAI T, et al. New design of a compact parallel micro-nano two-fingered manipulator hand [C]//IEEE International Conference on Nano/Micro Engineered and Molecular Systems. 2007: 515-519.

[7] LI Q, HERVE J-M. Type synthesis of 3-DOF RPR-equivalent parallel mechanisms[J]. Robotics IEEE Transactions on, 2014, 30(6): 1333-1343.

[8] SHEN H, YANG T, MA L. Synthesis and structure analysis of kinematic structures of 6-DoF parallel robotic mechanisms [J]. Mechanism & Machine Theory, 2005, 40(10): 1164-1180.

[9] 沈惠平, 赵海彬, 邓嘉鸣, 等. 基于自由度分配和方位特征集的混联机器人机型设计方法及应用[J]. 机械工程学报, 2011, 47(23): 56-64.

[10] 叶伟, 方跃法, 郭盛, 等. 基于运动限定机构的可重构并联机构设计[J]. 机械工程学报, 2015, 51(13): 137-143.

[11] JUNG H K, CRANE C D, ROBERTS R G. Stiffness mapping of compliant parallel mechanisms in a serial arrangement[J]. Mechanism & Machine Theory, 2008, 43(3): 271-284.

[12] LIU H, HUANG T, MEI J. Kinematic design of a 5-DoF hybrid robot with large workspace/limb-stroke ratio[J]. Journal of Mechanical Design, 2007, 129(5): 530-537.

[13] 李秦川, 柴馨雪, 陈巧红, 等. 2-UPR-SPR并联机构转轴分析[J]. 机械工程学报, 2013, 21(21): 62-69.

[14] BANDDYPADHYAY S, GHOSAL A. Analytical determination of principal twists in serial, parallel and hybrid manipulators using dual vectors and matrices[J]. Mechanism & Machine Theory, 2004, 39(12): 1289-1305.

[15] 曾达幸, 胡志涛, 侯雨雷, 等. 基于螺旋理论的两转一移解耦并联机构型综合[J]. 燕山大学学报, 2014, 38(1): 22-28

[16] 张曙, HEISEL U. 并联运动机床[M]. 北京: 机械工业出版社, 2003.

[17] 吴振勇, 王玉茹, 黄田. Tricept机器人的尺度综合方法研究[J]. 机械工程学报, 2003, 39(6): 22-25.

[18] 李彬, 黄田, 刘海涛, 等．Exechon混联机器人三自由度并联机构模块位置分析[J]. 中国机械工程, 2010, 21(23): 2785-2789.

[19] OZGUR E, DANMOUCHE R, ANDREFF N, et al. A vision-based generic dynamic model of PKMs and its experimental validation on the Quattro parallel robot[C]//Advanced Intelligent Mechatronics (AIM), 2014 IEEE/ASME International Conference on. 2014: 937-942.

[20] 吴孟丽, 黄田, 张大卫, 等. 一种新型可重构装备TriVariant的概念设计[J]. 机械设计, 2004, 21(增刊1): 28-30.

[21] 杨喜飞. 混联机器人的类型及其分析[J]. 科技创新与应用, 2015(21): 33.

[22] MANDELBORT B. How long is the coast of Britain? Statistical self-similarity and fractional dimension[J]. Science, 1967, 155(3775): 636-638.

[23] 文志英. 分形几何的数学基础[M].上海: 上海科技教育出版社, 2000.

[24] 曾强. 具有串并混联形式与变自由度特性的空间多环机构的拓扑设计方法[D]. 北京: 北京交通大学机械与电子控制工程学院, 2012.

[25] ZENG Q, FANG Y. Structural synthesis of serial-parallel hybrid mechanisms based on representation and operation of logical matrix[J]. Journal of Mechanisms & Robotics, 2009, 1(4): 469-484.

[26] ZENG Q, FANG Y. Structural synthesis of serial-parallel hybrid mechanisms via group theory and representation of logical matrix[C]//International Conference on Information and Automation. IEEE, 2009: 1392-1397.

[27] 廖明, 刘安心, 沈惠平, 等. 面向计算机辅助分析的并联机构符号描述方法[J]. 农业机械学报, 2015, 46(7): 310-317.

[28] HERVé J M. The Lie group of rigid body displacements, a fundamental tool for mechanism design[J]. Mechanism & Machine Theory, 1999, 34(5): 719-730.

[29] LI Q, HUANG Z, HERVÉJ M. Type synthesis of 3R2T 5-DoF parallel mechanisms using the Lie group of displacements[J]. IEEE Transactions on Robotics & Automation, 2004, 20(2): 173-180.

(责任编辑: 徐惠华)

A Methodology for Type Design of Hybrid Robot Mechanism Based on Fractal Theory

GEShuyi1a,CAOYi1a, 1b, 2a, 2b,DINGZehua1a,ZHOURui1a,ZHUJingyuan1a

(a. School of Mechanical Engineering; b. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, 1. Jiangnan University, Wuxi 214122, China; a. State Key Laboratory of Mechanical System and Vibration; b. Key Laboratory of System Control and Information Processing, Ministry of Education, 2. Shanghai Jiao Tong University,Shanghai 200240, China)

In order to obtain the configuration of the hybrid robot, a novel structural design methodology is proposed based on the fractal theory which also could apply to solve the design problems of multipath atypical hybrid mechanism with horizontal branches. Firstly, the basic concept of the topological graph and the fractal theory are expounded. Secondly, the binary code that represents the kinematic pair and their position relationship is established. Then the route rule for dealing with the topological graph and the calculation rule of union-intersection-preserving for deriving the kinematic pair are defined. According to the fractal theory the topological graph after fractal process is equipped with applicable kinematic pairs, so that the holistic hybrid mechanism can be acquired. Finally, the structure of the hybrid mechanism with two-translation and one-rotation is achieved that demonstrates the validity of the methodology.

hybrid robot mechanism; topological graph; fractal theory; route rule; binary code

1671-0444 (2017)02-0242-09

2016-03-15

国家自然科学基金资助项目(50905075, 51505190)；江苏省"六大人才高峰"资助项目(ZBZZ-012)；系统控制与信息处理教育部重点实验室开放课题资助项目(scip201506)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)；江苏省食品先进制造装备技术重点实验室开放课题资助项目(FM-201402)

葛姝翌(1992—)，女，河北秦皇岛人，硕士研究生，研究方向为混联机构学理论及机器人技术.E-mail: geshuyi0105@foxmail.com 曹毅(联系人)，男，副教授，E-mail: caoyi@jiangnan.edu.cn

TH 112