隔震结构碰撞分析的改进Hertz-damp模型
2017-06-19赵大海李宏男
赵大海, 刘 勇, 李宏男,钱 辉, 刘 莎
(1. 燕山大学 建筑工程与力学学院, 秦皇岛 066004; 2. 大连理工大学 土木工程学院, 大连 116024;3. 郑州大学 土木工程学院, 郑州 450001)
隔震结构碰撞分析的改进Hertz-damp模型
赵大海1, 刘 勇1, 李宏男2,钱 辉3, 刘 莎1
(1. 燕山大学 建筑工程与力学学院, 秦皇岛 066004; 2. 大连理工大学 土木工程学院, 大连 116024;3. 郑州大学 土木工程学院, 郑州 450001)
碰撞是一复杂的非线性问题,为了研究碰撞作用下结构的响应,合理的碰撞模型是非常必要的。针对隔震结构的碰撞现象,结合改进的Kelvin模型和Hertz-damp模型构造了一个新的阻尼函数,提出了改进的Hertz-damp碰撞模型,并对新碰撞模型的可靠性进行了数值验证。通过现有的碰撞试验和其他碰撞模型对比,表明改进后的Hertz-damp碰撞模型较其他碰撞模型具有较高的精度,能更精确地模拟结构的碰撞响应。
数值分析;Hertz-damp模型;结构碰撞;地震
现代城市人口密集,但土地非常有限,建筑之间的距离越来越近。由于建筑形态和功能的需要,或是结构抗震的要求,相邻建筑物之间的间距相对较小。因此,在强烈地震作用下,相邻结构间往往会发生碰撞,并造成重大的人员伤亡和财产损失。比如,1985年的墨西哥地震,建筑物发生了严重破坏或倒塌,其中40%是由于发生了碰撞导致的。另外,1994年北岭地震,1995年神户地震,1999年集集大地震和2008年汶川地震中,都有观察到碰撞现象的发生[1]。研究表明,结构碰撞对结构的地震反应和抗震性能有着重要的影响,随着建筑密度的增加,建筑结构的碰撞问题已成为防震减灾工程的重要研究课题[2]。
碰撞是一种复杂的非线性问题,为了有效地研究结构在碰撞作用下的响应,合理的碰撞分析模型是非常重要的。国内外学者对碰撞模型进行了一系列的研究。比如,Ye等[3]改进了Kelvin碰撞模型中阻尼系数的表达式。为了更好的模拟碰撞过程中力和位移的关系,一些学者采用Hertz理论模型来研究结构的碰撞响应。比如,Jankowski[4]提出了一种基于Hertz接触模型的非线性黏弹性模型,推导出了非线性黏弹性碰撞模型中阻尼常数的表达式,其中阻尼常数与恢复系数有关,并通过数值仿真进行了验证。但是,Hertz模型没有考虑碰撞过程中的能量损失,Muthukumar等[5]用Hertz-damp模型对结构的碰撞影响进行分析,并与其它碰撞模型进行了比较。
本文对已有的碰撞模型进行了回顾,并基于改进的Kelvin模型和Hertz-damp模型构建了一种新的阻尼函数,提出了改进的Hertz-damp模型,采用MATLAB/ Simulink对现有的碰撞试验进行数值模拟,并将改进碰撞模型的结果同其它碰撞模型的模拟结果进行了比较和分析。
1 已有的碰撞模型
目前,经典动力法和接触单元法是研究结构碰撞的主要方法。经典动力法进行数值分析时不方便,一般很少使用;接触单元法通过建立碰撞力对结构碰撞分析的数学模型,在碰撞部位加设接触单元,利用等效弹簧单元和等效阻尼单元来模拟结构碰撞过程中的相互作用和能量耗散,并在碰撞发生时接触、结束时脱离,所以被广泛使用。


图1 结构碰撞分析模型Fig.1 Analysis model for structural pounding
1.1 线弹性模型
线弹性模型是最简单的碰撞分析模型,其碰撞力的数学表达式为
(1)
式中:kl是线弹性模型的碰撞刚度;δ是两碰撞体的相对位移。该模型没有考虑碰撞过程中的能量损失,碰撞力与相对位移成线性关系。
1.2 Kelvin模型
Kelvin模型的应用最为广泛,加入线性黏性阻尼是考虑了碰撞过程中的能量损失,碰撞力表示为
(2)

(3)
式中:m1和m2分别是碰撞物体的质量;ξ是对应的阻尼常数,它与恢复系数e有关,其表达式为
(4)
线弹性碰撞模型的缺点是,黏性阻尼系数在整个碰撞过程中保持不变,这就导致在碰撞开始反弹的过程中能量损失的变化是均匀的。同时,Kelvin模型会造成碰撞力在开始阶段出现拉力,在反弹阶段的出现飞跃,这些现象都是与实际碰撞事实不相符的。
1.3 改进的Kelvin模型
基于Kelvin模型存在的不足之处,Ye等修正了Kelvin模型中的阻尼常数,提出了改进的Kelvin模型,并对其进行了验证。碰撞力的表达式与式(2)相同,修正后ξ的阻尼常数的表达式如下
(5)
式中:v1和v2分别是两碰撞体初始时刻的速度;kK是Kelvin模型的碰撞刚度。
1.4 Hertz模型
碰撞过程中,碰撞力的增加是非线性的。为了更准确地模拟结构碰撞的过程,一些学者对Hertz理论进行了研究。基于Hertz理论的碰撞力可以表示为
(6)
式中:δ是两碰撞物体的相对位移;kH是Hertz模型的碰撞刚度,该模型没有考虑碰撞过程中的能量损失。
1.5 Hertz-damp模型
Hertz-damp模型中增加了非线性阻尼项,从而弥补了Hertz模型没有考虑能量损失的不足,碰撞力可以表示为
(7)

cH=ξδ3/2
(8)
阻尼常数ξ、非线性刚度kH、恢复系数e和结构碰撞的相对初始速度δ之间的关系表示为
(9)
在非线性黏弹性模型中,当ξ=0时表示碰撞为完全弹性碰撞;ξ=∞当时表示碰撞为完全塑性碰撞[6]。从式(9)可以看出,当e=1且ξ=0时符合完全弹性碰撞;当e=0且ξ≠∞时却不符合完全塑性碰撞。因此,Hertz-damp模型在碰撞模拟中存在一定的误差。
2 改进的Hertz-damp模型
在已有碰撞模型理论的基础上,根据改进后的Kelvin模型和Hertz-damp模型,构造了一个新的碰撞阻尼函数,提出了一种改进的Hertz-damp模型。
对于改进后的Kelvin模型的阻尼系数,可以如式(8)一样表示为
cK=ξδ
(10)
将式(5)和式(10)代入式(2),得到下列表达式
(11)
式(11)可以改写成
(12)
从式(12)可以看出
(13)
通过式(13)可以得出
(14)
将式(14)代入式(7)中,得到改进的Hertz-damp模型的表达式为:
(15)
通过式(15)可以看出,改进Hertz-damp模型的阻尼系数是与碰撞刚度、接触初始时刻的相对速度、恢复系数和碰撞变形相关的函数。同时也可以看出,改进的Hertz-damp模型与Jankowski提出的非线性黏弹性模型理论相符合。
3 数值验证
本文采用改进的Hertz-damp模型对碰撞试验进行了模拟,并将试验结果和其它碰撞模型的结果进行了比较,验证了改进Hertz-damp模型的正确性和准确性。试验结果通过标准误差计算比较,误差公式[7]如下
(16)
式中:E是数值模拟的相对误差;F是试验中得到的响应时程;F′是数值分析得到的响应时程;‖F-F′‖是(F-F′)的欧氏范数,当把它看作一个离散值时,可以通过以下形式得到

(17)
式中:i是记录时程数值时间间隔的序号;n是时程数值的总个数。
3.1 钢球碰撞试验的模拟及数值分析
本节分别采用线弹性模型、Kelvin模型、Hertz模型、Hertz-damp模型和改进的Hertz-damp模型来模拟Goland等做过的碰撞试验,实验模型如图2所示。将不同直径的钢球从不同水平高度自由释放,下端放有刚性杆支撑的半球型刚体,同时刚性杆的下端与弹簧相连接以消除应力波的影响,用于数值计算的分析模型如图3所示。

图2 试验模型 图3 数值模型Fig.2 Experimental model Fig.3 Numerical model
通过分析得出了碰撞模型中钢球的动力平衡方程,其形式如下
(18)

δ(t)=y(t)-h
(19)
式中:y(t)是其竖向位移;h是钢球下落的高度。
采用不同的碰撞模型,对不同直径的钢球从不同高度进行了碰撞分析。本文选用一组数据进行数值模拟,选取的钢球直径为0.397 cm,跌落高度为5.08 cm,测试的最大冲击力为80.7 N。通过MATLAB/Simulink编写程序求解式(18),通过试算,当恢复系数为0.9时,采用Kelvin模型、Hertz-damp模型和改进的Hertz-damp模型得到的碰撞力时程误差都比较小。
图4比较了恢复系数为0.9时,不同碰撞模型的碰撞力时程,接触力-位移关系如图5所示。从图4可以看出,Kelvin模型误差较大的原因是碰撞力在接触初始阶段有跳跃,而且在回弹阶段出现拉力,这显然与碰撞的物理事实不符。从图5可以看出,Kelvin模型、Hertz-damp模型和改进的Hertz-damp模型的接触力-位移关系曲线有明显的滞回环,这是因为这三种碰撞模型都考虑了碰撞过程中的能量损耗,滞回环的面积表示碰撞过程中的能量耗散。线性弹性模型和Hertz模型的接触力-位移关系曲线是直线,表明它们在碰撞过程中没有考虑能量耗散。

图4 不同碰撞模型的碰撞力时程比较Fig.4 Comparisons on pounding force time histories for various impact models

图5 不同碰撞模型的撞击力-碰撞变形关系Fig.5 Contact force-displacement relationships for various impact models
表1给出了各种碰撞模型的参数和碰撞力时程误差。从表中可以看出,Hertz模型的碰撞力时程误差比较小,其原因为:钢球与半球之间的碰撞试验中弹性碰撞占据主导地位,碰撞过程中的能量损失较小。改进后的Hertz-damp模型在碰撞接触阶段与试验数据之间的差异较小,但在回弹阶段的差异呈增加趋势,其误差为27.05%,稍大于没有考虑能量耗散的Hertz模型的结果。同时,忽略碰撞过程中的能量耗散会高估结构碰撞的破坏程度。如果不考虑能量耗散,线弹性模型模拟得到的最大碰撞变形将大于Kelvin模型的结果,Hertz模型模拟得到的最大碰撞变形将大于Hertz-damp模型和改进Hertz-damp模型的结果。
3.2 隔震结构模型与运动方程
隔震结构的碰撞模型如图6所示,假定结构的质量集中在楼板处[8],则地震作用下结构碰撞的运动方程表示为[9]
(20)

隔震层的运动方程为
(21)
式中:mb和Fb分别表示隔震层的质量和恢复力;k1和c1分别为第一层的层间刚度和阻尼。

表1 各碰撞模型的参数及撞击力时程误差Tab.1 Parameters and errors of pounding force time history for various impact models
隔离层与限位装置发生碰撞时的方程为
(22)

LRB隔震支座的刚度和阻尼可以通过下面两个参数来求得[11],即隔震周期Tb和阻尼比ξb分别为
(24)
(25)

3.3 数值算例及分析
本节以五层隔震结构为例分析[12],隔震结构上部各层的质量为5×105kg,刚度为1×109N/m,采用瑞利阻尼,阻尼比为0.05。隔震层采用LRB支座,其质量为5.5×105kg,屈服位移为0.01 m,屈服强度为1.93×106kN,屈服后刚度为1.93×106N/m。经计算,非隔震结构的基本周期为Ts=0.494 s,隔震结构的基本周期为Tb=2.5 s。以Loma Prieta地震波作为输入,其时程曲线如图7所示。
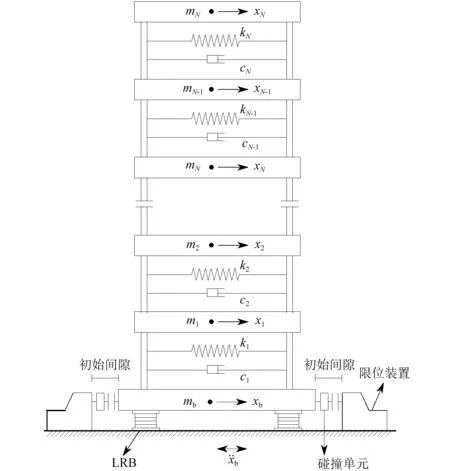
(a) 基础隔震结构模型

(b) 碰撞单元图6 基础隔震结构模型及碰撞单元Fig.6 Model of base-isolated structure and impact element

图7 Loma Prieta地震波时程Fig.7 Time history of Loma Prieta earthquake
图8分别给出了Loma Prieta地震波作用下,隔震结构顶层的加速度时程、碰撞力和基底剪力时程。从图中可以看出,与非隔震结构相比,考虑碰撞时,结构顶层的加速度峰值明显增大,尤其是在发生碰撞的隔震层处,加速度的增大更加显著。

(a) 顶层加速度时程

(b) 初始间隙为10 cm时的碰撞力时程

(c) 初始间隙为10 cm时的基底剪力时程图8 Loma Prieta地震作用下的结构响应时程Fig.8 Time history responses under Loma Prieta earthquake
表2给出了不同碰撞模型下基础隔震结构的峰值响应,其中初始预留间隙为10 cm。从表中可以看出,不同碰撞模型下基础隔震结构峰值之间的差异非常小,都在10%以内。但是,随着碰撞能量的增加,碰撞模拟的误差也随之增大,因此有必要考虑碰撞过程中的能量耗散。
图9给出了非隔震结构、不考虑碰撞的隔震结构以及考虑碰撞的隔震结构(初始预留间隙分别为5 cm和10 cm)下结构层间位移和绝对加速度的峰值。从图中可以看出,与不考虑碰撞的隔震结构相比,考虑碰撞时隔震结构的最大加速度和层间位移均有所增加,并且隔震层的加速度增大更为显著,隔震结构下部受到的影响比上部更为明显。从图中还可以看出,尽管改进的Hertz-damp模型和Hertz-damp模型数值模拟的结果差别不大,但是改进的Hertz-damp模型理论上克服了Hertz-damp模型的不足,与实际情况更为接近。

表2 不同碰撞模型的峰值响应对比Tab.2 Comparisons on peak responses for different impact models

(a) 最大层间位移

(b) 最大绝对加速度图9 Loma Prieta地震作用下结构的峰值响应Fig.9 Peak responses of structure under Loma Prieta earthquake
4 结 论
本文基于改进的Kelvin模型和Hertz-damp模型构建一个新的阻尼函数,提出了改进的Hertz-damp模型,并对新碰撞模型的可靠性进行了数值验证,主要结论如下:
(1)本文提出的改进Hertz-damp模型,克服了现有碰撞模型的缺点,对结构碰撞模拟具有较高的精度,能更准确地模拟结构的碰撞响应。
(2)当碰撞过程中能量耗散较大时,可以采用改进的Hertz-damp模型和Hertz-damp模型用来模拟碰撞,而线弹性模型、Hertz模型和Kelvin模型不适用于较大的能耗碰撞模拟。
(3)改进的Hertz-damp模型克服了Hertz-damp模型的不足,与不考虑碰撞的隔震结构相比,考虑碰撞时隔震结构的最大加速度和层间位移均有所增加,并且隔震层的加速度增大更为显著。
[1] NAEIM F, LEW M, HUANG S C, et al. The performance of tall buildings during the 21 September 1999 Chi-Chi earthquake, Taiwan [J]. The Structure Design of Tall Building, 2000, 9(2): 137-160.
[2] WANG Zifa. A preliminary report on the Great Wenchuan Earthquake [J]. Earthquake Engineering and Engineering Vibration, 2008, 7(2): 225-234.
[3] YE Kun, LI Li, ZHU Hongping. A modified Kelvin model for pounding simulation of base-isolated structures with adjacent structures under near-fault ground motions [J]. Earthquake Engineering and Engineering Vibration, 2009, 8(3): 433-446.
[4] JANKOWSKI R. Non-linear viscoelastic modeling of earthquake-induced structural pounding [J]. Earthquake Engineering and Structural Dynamics, 2005, 34(6): 595-611.
[5] MUTHUKUMAR S, DESROCHES R. A Hertz contact model with non-linear damping for pounding simulation [J]. Earthquake Engineering and Structural Dynamics, 2006, 35(7): 811-828.
[6] JANKOWSKI R. Analytical expression between the impact damping ratio and the coefficient of restitution in the non-linear viscoelastic model of structural pounding [J]. Earthquake Engineering and Structural Dynamics, 2006, 35(4): 517-524.
[7] 许祥, 刘伟庆, 徐秀丽. 结构地震碰撞分析的线性黏弹性碰撞模型[J]. 工程力学, 2013, 30(2): 278-284.
XU Xiang, LIU Weiqing, XU Xiuli. Linear viscoelastic model of earthquake-induced structural pounding [J]. Engineering Mechanics, 2013, 30(2): 278-284.
[8] 黄潇, 朱宏平. 近断层地震作用下相邻隔震结构的碰撞研究[J]. 土木工程与管理学报, 2011, 28(3):249-253.
HUANG Xiao, ZHU Hongping. Study on impact of adjacent base-isolated structures under near-fault earthquake [J]. Journal of Civil Engineering and Management, 2011, 28(3): 249-253.
[9] 邹立华, 郭润, 黄凯, 等. 带预应力橡胶支座相邻隔震结构碰撞分析[J]. 振动与冲击, 2014, 33(9): 131-136.
ZOU Lihua, GUO Run, HUANG Kai, et al. Pounding of adjacent isolated-structures with prestressed rubber bearings [J]. Journal of Vibration and Shock, 2014, 33(9): 131-136.
[10] 赵建伟, 邹立华, 方雷庆. 考虑相邻建筑物碰撞的基础隔震结构的地震反应分析[J]. 振动与冲击,2010, 29(5): 215-219.
ZHAO Jianwei, ZOU Lihua, FANG Leiqing. Seismic response analysis of base-isolated structures considering pounding of adjacent building [J]. Journal of Vibration and Shock, 2010, 29(5): 215-219.
[11] MATSAGAR V A, JANGID R S. Seismic response of base-isolated structures during impact with adjacent structures [J]. Engineering Structures, 2003, 25(12): 1311-1323.
[12] KOMODROMOS P, POLYCARPOU P C, PAPALOIZOU L, et al. Response of seismically isolated buildings considering poundings [J]. Earthquake Engineering and Structural Dynamics, 2007, 36(12): 1605-1622.
Modified Hertz-damp model for base-isolated structural pounding
ZHAO Dahai1, LIU Yong1, LI Hongnan2, QIAN Hui3, LIU Sha1
(1. School of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao 066004, China;2. School of Civil Engineering, Dalian University of Technology, Dalian 116024, China;3. School of Civil Engineering, Zhengzhou University, Zhengzhou 450001, China)
Pounding is a complicated nonlinear problem. In order to investigate the structural responses under the impact of collision, a proper collision model was very necessary. For the impact of base-isolated structure, a new damping function was constructed by combining the modified Kelvin model and the Hertz-damp model. The modified Hertz-damp model was proposed, and the reliability of the new impact model was verified by numerical simulation. Comparing with other impact models according to the existing pounding tests, it can be shown that the modified Hertz-damp model is more accurate than the other impact models, and can accurately simulate the pounding responses of the structure.
numerical analysis; Hertz-damp model; structural pounding; earthquake
国家自然科学基金资助项目(51308487; 41402261);河北省自然科学基金资助项目(E2014203055);河北省高等学校科学技术研究项目(YQ2013015);河北省大学生创新创业训练计划项目(201610216025)
2016-03-21 修改稿收到日期: 2016-09-03
赵大海 男,博士,副教授,1980年生
刘勇 男,硕士生,1990年生
TU352.1
A
10.13465/j.cnki.jvs.2017.12.038
