驱动链高速轴断裂所致FAST索牵引并联机器人的冲击振动仿真分析

李 辉， 潘高峰

(1. 中国科学院 国家天文台，北京 100012； 2. 中国科学院 射电天文重点实验室，北京 100012)

驱动链高速轴断裂所致FAST索牵引并联机器人的冲击振动仿真分析

李 辉1,2， 潘高峰1,2

(1. 中国科学院 国家天文台，北京 100012； 2. 中国科学院 射电天文重点实验室，北京 100012)

介绍了FAST望远镜的巨型柔索牵引并联机器人的构型和工作方式。对FAST柔索牵引并联机器人的塔-索-舱柔性悬挂系统在某一套索驱动单元的电机高速轴发生断裂，卷筒上的低速轴安全制动器随即启动的极端工况所引发的卷筒溜索量和柔性悬挂系统的冲击振动力进行了有限元仿真分析；总的仿真分析可分为三步进行，即柔性悬挂系统的静力学找形分析、卷筒溜索量分析和基于溜索量-时程曲线的系统动力学仿真分析；与此同时，仿真中采用了模拟塔柔性的质量-弹簧振子模型、简化的安全制动器制动力时程曲线和模拟索驱动设备的绳索-质量滑块系统等简化模型。计算结果表明，因高速轴断裂引发的冲击造成了柔性悬挂系统的大幅震荡，需要在系统详细设计中认真考虑。

FAST望远镜；索牵引并联机器人；高速轴断裂；冲击振动；动力学仿真

正在中国贵州省建造的500 m口径球面射电望远镜FAST(Five-hundred-meter Aperture Spherical radio Telescope)是国际现有和正在计划建造的最大单口径射电天文望远镜，其独特的馈源舱柔索支撑系统是FAST望远镜的主要创新和关键技术之一，也是典型的柔索牵引并联机器人，如图1所示。FAST柔索牵引并联机器人由6条柔性钢索并联牵引直径约13 m、质量约30 t的馈源舱悬浮于空中，每条钢索依赖一座100 m高塔作为支撑架，其跨度达300 m。FAST柔索牵引并联机器人尺度巨大，柔索垂度明显，作为终端控制平台的馈源舱运动缓慢，但其位姿定位精度要求较高，且与柔索牵引并联机器人的动力学性能关系密切。

图1 FAST望远镜效果图Fig.1 Effect picture of FAST telescope

对柔索的动力学建模是研究索牵引并联机器人动力学性能的关键。文献[1]对悬索动力学领域的研究进展进行了较为详细的总结，包括动力学建模、动力学分析、动力学实验等，但这些研究都以单根柔索为分析对象，并不完全适合于索牵引并联机器人所具有的多索并联悬挂系统。关于索牵引并联机器人动力学建模与分析的专门文献目前并不多见，早期的研究工作[2-3]因研究对象的尺度和工作空间较小，将柔索简化为仅承受拉力的直线单元，不考虑悬索垂度和自身振动，与FAST柔索牵引并联机器人的实际相差较大。一些文献针对FAST索牵引并联机器人的动力学特性进行了专门研究，例如关于舱-索系统动力学建模及在风扰下的振动分析[4-5]；从数值模型和理论推导方面探讨悬索系统刚度、频率与悬索张力及位形的关系[6-10]；分析支撑塔的柔性对舱-索系统振动的影响, 建议支撑塔的刚度和频率应大于一定的临界值，以防止塔振动造成舱-索系统的共振[11]；从振动控制的方面探讨馈源舱定位控制算法和舱-索系统控制的稳定性[12-14]；提出了一种柔索长度慢速变化时的索牵引并联机器人动力学模型[15-16]等。

上述研究工作主要集中于分析FAST柔索牵引并联机器人在正常工况下的动力学性能及其对终端平台-馈源舱的位姿定位控制的影响，此时柔索及舱偏离其平衡位置进行小幅振动，索张力和系统加速度等物理量较小。在极端工况下，FAST柔索牵引并联机器人可能在短时间内承受巨大冲击作用。例如，某一钢索因驱动机构高速轴突然断裂在短时间内失去驱动力和制动力而快速坠落，然后被安全制动器制动抱闸，导致系统在短时间内因失去平衡而产生大幅震荡。在此工况下，无论柔索、馈源舱和柔索驱动链均将承受极大的冲击载荷和加速度场，对机构元件的极限承载能力和附属设备的极限生存能力均是严峻的考验，而关于此类情况下的柔索牵引并联机器人动力学建模和分析却尚未见刊载。文献[17]基于能量守恒原理初步计算了FAST柔索牵引并联机器人在上述极端工况下所需的制动摩擦力，但该方法没有建立系统的动力学模型，多数物理量根据经验估计或试算得到，如制动距离的取值，缺乏有说服力的依据。

本文通过有限元仿真分析在极端工况下FAST索牵引并联机器人中舱-索-塔系统的大幅震荡，计算在给定的最大制动力作用下的制动距离和制动作用时间，同时计算由此引起的6根钢索的动态冲击索力和其它一些需要关注的物理量，如馈源舱最大振幅、加速度等，为钢索及舱内设备等的抗冲击设计提供足够的计算依据。

1 高速轴断裂工况的基本过程分析

FAST柔索牵引并联机器人包含6套并联的柔索驱动机构。其单套驱动机构包括电机、联轴器(高速轴)、减速机和卷筒(低速轴)，通过塔底滑轮和塔顶滑轮的二次导向，使钢索能够支撑并驱动馈源舱在空间运动，如图2所示。馈源舱的运动轨迹集合为一球冠状轨迹面，其在焦面范围运动时的6条索张力和索长变化范围是进行索驱动机构和钢索选型设计的重要依据参数。李辉等[18]按照索力均衡分配的优化原则计算了6条索索张力和索长的变化范围，在正常运行时钢索所承受的张力约为130～300 kN，当驱动馈源舱在轨迹焦面运动时，钢索长度变化变化范围为220～420 m。

(a)

(b)图2 FAST柔索牵引并联机构单套索驱动链Fig.2 A set of chain drive of FAST CDPR

由于FAST馈源舱由6套钢索驱动机构并联支撑和驱动，任何一套驱动机构出现故障，均对馈源舱的运行产生巨大的影响。高速轴断裂时，由相关传感器发出故障代码，索牵引并联机器人控制系统检测到故障后立即启动该套索驱动机构的低速轴安全制动器，使得卷筒制动，同时启动其余5套索驱动机构的高速轴制动器，使得馈源舱在空中悬停。具体过程如下：

(1) 从高速轴突然断裂到低速轴安全制动器开始启动并对卷筒施加制动扭矩需要一段时间，通常设定约为0.5 s。在此时间段内，电机的输出扭矩被切断，所对应的钢索瞬间失去动力牵引，馈源舱失去静力平衡。在卷筒出绳端钢索承受的索力仅为卷筒等机构被动放绳的惯性力，钢索在其余5条索和馈源舱的反拽力、滑车重量及自身重力作用下加速下坠，引发馈源舱加速下坠；

(2) 高速轴断裂0.5 s后，低速轴安全制动器启动，制动力作用到卷筒制动盘，然后转化到钢丝绳上的反拽索力，其值假设为恒定150 kN，如图3所示。其它5台工作正常的卷扬机也同时实现高速轴紧急制动抱闸，停止收/放绳。

(3) 高速轴断裂所对应的钢索在低速轴安全制动器的制动力作用下下坠速度减缓，乃至最后停止下坠，卷筒停止溜索，其溜索量及卷筒被制动停止的时间需要由仿真计算确定。

(4) 索牵引并联机器人系统形成新的静力平衡点，但馈源舱在惯性力及下坠速度驱使下继续反复穿越该平衡点，形成大幅震荡，引发舱内设备的加速度场和速度场，并引发6条索索力的震荡，形成脉动冲击索力。在系统自身的阻尼作用下，震荡在经历数十个周期后逐步减弱并消失，系统重新静止于新的静力平衡点位置。

图3 低速轴安全制动器的制动力-时程曲线Fig.3 Force-time curve of safety brake on low speed shaft

2 塔-索-舱柔性悬挂系统的有限元建模及其仿真过程分析

在FAST索牵引并联机器人系统中，由塔、并联6条索和舱所构成的柔性悬挂系统是影响机器人系统动力学性能的主要因素，因此对FAST索牵引并联机器人系统的动力学仿真主要围绕塔-索-舱柔性悬挂系统进行，仿真分析采用有限单元法实现，同时对驱动机构进行必要的简化建模。塔-索-舱柔性悬挂系统有限元模型，如图4所示。柔索被简化为质量均匀分布的单向受拉杆单元，单元长度足够小，较多数量的串联受拉杆单元可以较好地模拟悬索曲线。相对于悬索，馈源舱可看成6自由度刚体，仅保留主体承重框架结构，含馈源舱的总质量；支撑塔柔性简化为水平弹簧-等效质量振子模型。水平弹簧有两个自由度，且刚度相等，振子固有频率为1 Hz，等于塔一阶固有频率。此外，考虑到其他因素的影响，作者进一步采用了如下的假设：

1) 忽略塔-索-舱悬挂系统的缓慢运动。高速轴断裂之前，塔-索-舱悬挂系统处于静止状态且满足静力平衡条件；

2) 因高速轴断裂前后塔-索-舱系统处于静止状态，其余5条钢索卷扬机同时抱闸对塔-索-舱系统不产生影响；

3) 高速轴断裂后低速轴安全制动器启动时的制动力-时程曲线，如图3所示；

4) 卷扬机抱闸后，塔顶滑轮以下部分钢索及驱动机构对柔性悬挂系统影响不大，除高速轴断裂所对应的钢索外，其余5条柔索的仿真模型截止到塔顶滑轮出索点；

5) 高速轴断裂所对应的钢索及索驱动设备的仿真模型简化为绳索-质量滑块系统，如图5(b)所示，须换算滑块的等效质量；

6) 因高速轴断裂引发的卷筒溜索量占单根钢索总长度的比率很小，忽略因溜索引起的塔-索-舱系统和绳索-质量滑块系统的质量变化。

图4 塔-索-舱柔性悬挂系统的有限元仿真模型Fig.4 Finite element model of the tower-cable-cabin flexible suspension system

考虑到悬索的柔性和垂度，塔-索-舱柔性悬挂系统为几何非线性力学系统，重力场和悬索位形对系统刚度有很大的影响，其动力学分析须考虑几何非线性因素。为保障系统特别是悬索振动计算的收敛，对于在振动中可能处于虚牵状态的索4，在其跨中的4个索节点处增加了8个人工黏性阻尼单元，其方向垂直于索曲线的切线方向。黏性阻尼单元的阻尼与索节点的速度成正比关系，其阻尼系数通过试算后取上限2 000 N/(m/s)，防止中间过程的钢索动位移计算值过高而导致计算结果发散，同时保证引入的人工黏性不至于对柔性悬挂系统的计算结果造成大的影响。表1所示为仿真模型所采用的模型计算参数。所采用右手螺旋直角坐标系以焦面最低点为原点，竖直向上为Z轴正向，塔1和塔6所成夹角平分线为X轴正向。

(a) 卷筒-钢索-滑轮系统

(b) 简化的绳索-质量滑块模型图5 高速轴断裂所对应的钢索及索驱动设备的仿真模型Fig.5 Models of cable and chain drive for the simulation of high-speed shaft rupture表1 仿真模型计算参数Tab.1 Computational parameters of the simulation model

位置点X/mY/mZ/m馈源舱WP1000WP281.0964.9937.82WP342.5994.7937.82支撑塔塔1258.21149.07133.24塔27.99298.15133.24塔3-258.21149.08133.24塔4-258.21-149.07133.24塔5-2.40-298.15133.24塔6258.21-149.08133.24塔顶滑轮转动惯量J3/(kg·m2)298馈源舱总质量/kg30062地滑轮转动惯量J2/(kg·m2)298钢索线密度/(kg·m)9.9卷筒转动惯量J1/(kg·m2)15580钢索弹性模量/GPa108塔顶等效质量/kg153990钢索等效截面面积/mm21150.9塔-索-舱系统的固有阻尼比[18]0.22%塔顶与轨迹面中心点(WP1)高差/m110塔顶与轨迹面边缘点(WP2、WP3)高差/m110塔顶与轨迹面中心点(WP1)水平距离/m300轨迹面曲率半径/m161.67轨迹面口径/m206塔高/m100馈源舱重心位置(相对于舱-索铰接平面)/m-0.2

根据经验，6条索中张力最大的钢索所对应的高速轴容易发生突然断裂，此时对柔性悬挂系统的冲击也最大，因此作者选择在轨迹面边缘处的两点WP2和WP3作为柔性悬挂系统所对应的馈源舱位置，如图6所示。由此建立塔-索-舱柔性悬挂系统的动力学模型并进行仿真分析。此两点分别对应于索1张力达到最大值、索1和索2的张力同时达到最大值两种情况，均假设索1的高速轴发生突然断裂。

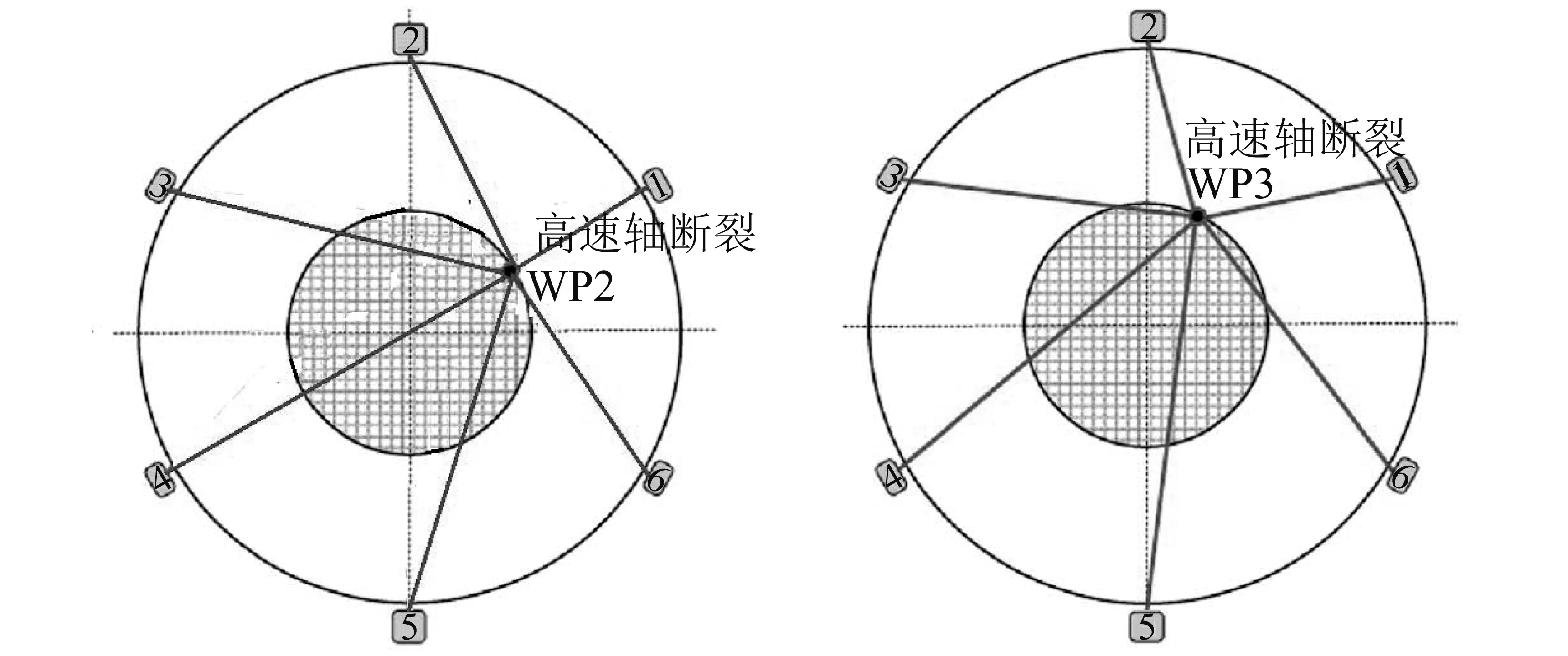
图6 仿真选取的馈源舱典型位置点Fig.6 Typical cabin positions selected for dynamic simulation

对于柔性悬挂系统的动力学仿真一般分为两个阶段。首先通过静力学分析寻找柔性悬挂系统处于平衡位置的位形，其次在平衡位形的基础上再进行系统的动力学分析。总体仿真工作可分为三步进行：

1) 先进行索-舱柔性悬挂系统的找形分析，即系统静力学分析，找到柔性悬挂系统的平衡状态及位置。文献[19]提供了馈源舱分别在轨迹面边缘点WP2和WP3并处于平衡优化状态的舱姿态及6索张力，参考表1中塔6塔顶和边缘点的坐标关系以及索悬链线模型，作者可推算索曲线方程，建立6条悬索的实体模型并在此基础上实现柔索单元的网格划分。由于索6的曲线是建立在索-舱系统静力平衡分析的基础上，由此得到的限元模型可最大限度逼近处于平衡状态的柔性悬挂系统，平衡后馈源舱位置与要求位置(WP2/WP3)的偏差<30 mm，姿态偏差<0.1°。

2) 分析从高速轴断裂发生后卷筒开始溜索到卷筒被完全制动这一阶段的柔性悬挂系统的响应，重点计算柔索下坠的总长度(溜索长度)和所需时间，这也是“3)”仿真计算的输入参数。

具体做法是在高速轴断裂所对应索1的索端节点增加集中质量单元，取图5(b)所示简化模型的等效质量，由此模拟溜索时卷筒、滑轮和塔下钢索的惯性对柔索下坠的拖拽作用；同时对该节点沿悬索弦线方向施加如图3所示的制动力时程曲线，模拟制动力对柔索下坠的阻尼作用；取消索1的索端节点沿悬索弦线方向的位移约束，通过塔顶索端节点沿悬索弦线方向的位移响应来模拟卷筒的溜索量，如图7所示。

3) 首先删除索1的索端节点沿悬索弦线方向的制动力。然后将第二步仿真计算得到的溜索量-时程曲线(上升段)作为索1的索端节点沿悬索弦线方向的动态输入位移。最后重新进行柔性悬挂系统的动力学分析。上述“1)”和“2)”的仿真均仅为“3)”仿真作准备和提供输入参数，“3)”的仿真才是模拟塔-索-舱柔性悬挂系统大幅震荡全程仿真，故仿真时间尽量长些，本文采用了23 s，其子步时间步长取0.01～0.05 s。

3 仿真结果分析

3.1 溜索量时程曲线

如图7所示，从高速轴断裂后0～0.5 s时刻，馈源舱连同钢索加速下坠，塔顶滑轮加速放绳，引发塔-索-舱系统的震荡，从图7中可以看出0～0.5 s的上升段曲线比较陡。0.5 s后低速轴安全制动器制动启动，然后钢索下坠减速，但塔顶滑轮放绳量继续增加，直到该过程终点时刻卷筒被制动刹停，塔顶滑轮停止放绳，钢索停止下坠，溜索量达到最大值，但塔-索-舱系统继续震荡。图7中的曲线上升段即为所求的溜索量时程曲线，也即为高速轴断裂后的卷筒转动量-时程曲线，对应时刻即为卷筒刹停的时间点。根据不同馈源舱位置点WP2和WP3的仿真结果，卷筒刹停的时刻均在高速轴断裂后约3 s，即低速轴安全制动器启动后其滑动制动时间持续约2.5 s，但滑动制动距离因不同舱位置而有所变化，其中在WP2位置时，制动距离达到最大值，约4.89 m。

卷筒刹停后，安全制动器的静摩擦力继续起作用，累计溜索量保持不变，但因仿真模型中在塔顶滑轮处仅施加了基于滑动摩擦力的恒定制动力，无法模拟静摩擦力，故仿真结果在卷筒刹停时刻以后继续给出了图7中的曲线下降段(虚线)。该段曲线并无实际物理含义。

图7 溜索量时程曲线Fig.7 Length-time curve of cable failing

3.2 塔-索-舱柔性悬挂系统大幅震荡的仿真

如上文所述，对仿真结果按WP2和WP3两个典型极端位置共2种组合进行了分组列表，对塔-索-舱系统振荡过程中的极端物理量值进行了统计，详见表2。经过比较，在WP2位置下，多数物理量的极端值最大，证实了最大静态索力位置决定了高速轴断裂这种极端工况发生后索驱动机构所须承受的最不利荷载。

在高速轴断裂所引发的冲击下，最大索张力发生在与断裂高速轴所对应钢索相邻的两条钢索中，在其舱索锚头处其索力峰值分别为471.7kN(WP2)和513.2kN(WP3)，其时程曲线，如图12所示。与此同时，舱的振荡位移、姿态角、速度、加速度等均达到了相当可观的峰值，如图8～图11所示。应当在馈源舱的详细设计中予以认真考虑，特别是设备在极端工况下的防冲击存活能力。

从表3可知，当振荡平息后，塔-索-舱系统在新的平衡位置所具有的舱姿态和索张力均将大大超出正常的设计值，如馈源舱俯仰角最大接近于22°，舱索铰接点处索力接近400kN，正常状态下两值分别为约15°和300kN。该异常状态不宜长期保持，建议索牵引并联机器人在承受最初的冲击并存活下来后，应尽快脱离此异常状态，启动极端工况下的5索控制使得舱姿态及索力保持在安全值以内。然后应继续启动5索控制使得馈源舱能够在故障工况下顺利下降至地面的停靠检修平台，对钢索、舱结构及舱内设备进行检修维护。这将是下一步需要深入研究的工作。

表2 系统震荡瞬时物理量最大值统计Tab.2 Statistics of maximal transient physical parameters during vibration

(a) WP2

(b) WP3图8 馈源舱中心点相对于原平衡位置的位移时程曲线Fig.8 Displacement-time curve of the cabin center relative to its original balanced position

图9 馈源舱振荡的姿态角时程曲线Fig.9 Orientation-time curve of the cabin

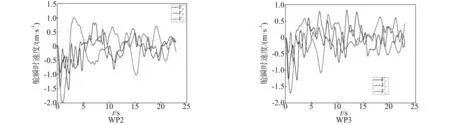
图10 馈源舱中心点震荡的速度时程曲线Fig.10 Speed-time curve of the cabin center

图11 馈源舱中心点震荡的加速度时程曲线Fig.11 Acceleration-time curve of the cabin center

图12 六索张力时程曲线Fig.12 Force-time curve of 6 steel cables表3 索1高速轴断裂前后的系统在各自平衡状态下的舱姿态和6索张力比较Tab.3 Cabin orientation and 6 cable tensions as the suspension system is under the respective equilibrium before/after high-speed shaft rupture

馈源舱位置馈源舱俯仰角/(°)馈源舱方位角/(°)馈源舱自旋角/(°)索张力(舱索铰接点处)/kN索1索2索3索4索5索6WP2断裂后21.59193.2310.38153.2359.2137.494.7109.2364.4断裂前15.22143.93-1.15295.3225.8161.8131.514.18215.6WP3断裂后17.41211.898.19162.8372.7153.4109.8126.9283.8断裂前15.49118.290.12269.1275.0186.1131.5130.8182.3

4 结 论

详细介绍了FAST柔索牵引并联机器人在某一驱动钢索所对应的高速轴发生突然断裂的极端工况，并分析了在该工况下从高速轴突然断裂、卷筒开始溜索、低速轴安全制动器随即启动、卷筒溜索被制动阻止、直至柔性悬挂系统大幅震荡的基本演变过程。

首次对FAST柔索牵引并联机器人的塔-索-舱柔性悬挂系统在极端工况下的冲击振动力学性能进行了有限元仿真分析。总体仿真分析分为三步进行，即柔性悬挂系统的静力学找形分析、卷筒溜索量分析和基于溜索量-时程曲线的系统动力学仿真分析。与此同时，仿真中采用了模拟塔柔性的质量-弹簧振子模型、简化的安全制动器制动力时程曲线和模拟索驱动设备的绳索-质量滑块系统等简化模型。计算结果证明分步骤进行的仿真策略和简化模型是可行的。

在仿真工作中选取了索张力最大的两个典型馈源舱位置进行了对比分析。仿真结果表明，在安全制动器启动后约2.5 s左右卷筒停止溜索，此时卷筒的最大溜索量约4.89 m，发生在WP2位置。高速轴断裂引发的最大冲击索力约为471.7 kN，发生在WP3位置。在两个典型馈源舱位置处，因高速轴断裂带来的冲击均造成了塔-索-舱柔性悬挂系统的大幅震荡和各项设计指标的大幅提高，需要在系统详细设计中认真考虑。

[1] 金栋平，文浩，胡海岩. 绳索系统的建模、动力学和控制[J]. 力学进展，2004，34(3): 304-313. JIN Dongping, WEN Hao, HU Haiyan. Modeling, dynamics and control of cable systems [J]. Advances in Mechanics, 2004, 34 (3): 304-313.

[2] OH S R, AGRAWAL S K. A reference governor based controller for a cable robot under input constraints [J]. IEEE Transactions on Control System Technology, 2005, 13(4): 639-645.

[3] FANG S, FRANITZA D, TORLO M, et al. Motion control of a tension-based parallel manipulator using optimal tension distribution [J]. IEEE/ASME Transactions on Mechatronics, 2004, 9(3):561-567.

[4] 虞黎明, 索双富, 季林红, 等. FAST一次支撑系统的实验研究 [J]. 空间科学学报, 2003, 23(1): 68-73. YU Liming, SUO Shuangfu, JI Linhong, et al. Experimental research of first feed-support system of FAST [J]. Chinese Journal of Space Science, 2003, 23(1):68-73.

[5] 魏强,仇原鹰,段宝岩. LT50m缩比模型悬索舱体系统的风振分析[J]. 应用力学学报, 2003, 20(1): 59-63. WEI Qiang, QIU Yuanying, DUAN Baoyan. Wind-induced vibration analysis of the cable-cabin suspension system of LT50m model [J]. Chinese Journal of Applied Mechanics, 2003, 20(1): 59-63.

[6] 杜敬利, 仇原鹰, 段宝岩. LT50m模型二级运动调整系统的动力学分析 [J]. 应用力学学报, 2006, 23(3): 453-458. DU Jingli, QIU Yuanying, DUAN Baoyan. Dynamic analysis to two-level kinetic tuning system of LT50m model[J]. Chinese Journal of Applied Mechanics, 2006, 23(3): 453-458.

[7] ZI Bin, DUAN Baoyan, DU Jingli, et al. Dynamic modeling and active control of a cable-suspended parallel robot [J]. Mechatronics, 2008, 18: 1-12.

[8] 訾斌, 段宝岩, 杜敬利. 柔索驱动并联机器人动力学建模与数值仿真[J]. 机械工程学报, 2007, 43(11): 82-88. ZI Bin, DUAN Baoyan, DU Jingli. Dynamic modeling and numerical simulation of cable-driven parallel manipulator [J]. Chinese Journal of Mechanical Engineering, 2007, 43(11): 82-88.

[9] 汤奥菲, 仇原鹰, 段宝岩. 大柔性Stewart平台的刚度研究[J]. 应用力学学报, 2006, 23(4): 678-681. TANG Aofei, QIU Yuanying, DUAN Baoyan. Stiffness study of a large flexible Stewart platform [J]. Chinese Journal of Applied Mechanics, 2006, 23(4): 678-681.

[10] 保宏, 杜敬利, 段宝岩. 大型射电望远镜悬索馈源支撑系统静刚度分析[J]. 机械工程学报, 2006, 42(7): 119-125. BAO Hong, DU Jingli, DUAN Baoyan. Analysis of stiffness of suspended feed system for large radio telescope [J]. Chinese Journal of Mechanical Engineering, 2006, 42(7): 119-125.

[11] 刘玉标, 申仲翰, 李世海. 悬索馈源系统的静动力分析与舞动评估. 创新工程重大项目KJX1-Y-01, 大射电望远镜FAST预研究总结报告, 附件九[R]. 北京: 中国科学院国家天文台大射电望远镜实验室, 2001.

[12] 清华大学FAST研究组. 大射电望远镜FAST移动小车-馈源稳定系统耦合研究[D]. 北京: 清华大学, 2003.

[13] 唐晓强. 完整的FAST馈源支撑机构缩尺模型验收报告[R]. 北京：清华大学，2010.

[14] 刘小光. FAST工程空间六索驱动馈源舱位姿控制系统整体控制策略[D]. 吉林：吉林大学，2015.

[15] 杜敬利，保宏，宗亚雳，等. 索牵引并联机器人中变长度柔索的动力学分析[J]. 振动与冲击，2011,30(8):19-23. DU Jingli, BAO Hong, ZONG Yali, et al. Dynamic analysis of cables with varying-length in cable-driven parallel robots [J]. Journal of Vibration and Shock, 2011, 30(8):19-23.

[16] 杜敬利，崔传贞，段清娟，等. 考虑柔索振动影响时索牵引并联机器人的动力学分析与控制[J]. 振动与冲击，2012,31(24):88-93. DU Jingli, CUI Chuanzhen, DUAN Qingjuan, et al. Dynamic analysis and control of a cable-driven parallel manipulator considering cable vibration effects[J]. Journal of Vibration and Shock, 2012,3(24)：88-93.

[17] 韩进城，徐宏伟，刘雪霞，等. FAST索驱动高速轴传动链故障保护方案[J]. 机械工程师,2014(2):49-51. HAN Jincheng, XU Hongwei, LIU Xuexia, et al. Protection scheme for the failure of high-speed shaft in cable drive system of FAST project [J].Mechanical Engineer, 2014(2): 49-51.

[18] 李辉，朱文白，潘高峰. 基于索力优化的FAST柔索牵引并联机构的静力学分析[J]. 工程力学， 2011，28(4):185-193. LI Hui, ZHU Wenbai, PAN Gaofeng. Equilibrium analysis of FAST rope-drive parallel manipulator based on rope force optimization [J]. Engineering Mechanics, 2011, 28(4):185-193.

[19] LI Hui, SUN Jinghai. Experimental study on the damping of FAST cabin suspension system[C] ∥Proc of SPIE. Amsterdam, 2012.

Simulation on high-speed-shaft-rupture-induced shock vibration of a cable-driven parallel robot of FAST

LI Hui1,2, PAN Gaofeng1,2

(1. National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012, China;2. Key Laboratory of Radio Astronomy, Chinese Academy of Sciences, Beijing 100012, China)

The configuration and working style of a huge scale cable-driven parallel robot (CDPR) of FAST telescope was introduced in the paper. Dynamic finite element analysis was specially done to simulate the complicate response of its flexible tower-cable-cabin suspension system under a kind of catastrophic accident that was caused by sudden rupture of the high-speed shaft of the motor within one certain cable-driven machine of the robot. As a result, the overbalanced steel cable began to fall and it in turn triggered the safety brake to function on the low-speed shaft of the cable drum and finally to stop the falling of the cable. The whole process was accompanied by the cable falling of the cable drum and then the following shock vibration of the flexible suspension system. The simulation was carried on three stages: first finding the equilibrium shape of the suspension system, then computing the cable falling on the drum, finally analyzing the shock vibration of the flexible suspension system with the input of time curve of the cable falling. Meanwhile a few simplified models were applied in the simulation, such as the model of mass-spring vibrator for the tower structure, the simplified force-time curve of the safety brake, the model of the rope-block sliding system, and so on. The simulation result shows that the overbalance shock by high-speed shaft rupture induces large scale vibration of the flexible suspension system, which should be considered seriously in the future design.

FAST telescope; cable-driven parallel robot; rupture of high-speed shaft; shock vibration; dynamic simulation

国家自然科学基金面上项目(11573044)

2015-10-27 修改稿收到日期： 2016-03-28

李辉 男，博士，副研究员，1973年生

E-mail：Lihui@nao.cas.cn

O322;TH113.1

A

10.13465/j.cnki.jvs.2017.12.013