冲击荷载作用下泄爆板破坏冲量计算与模拟

由泽伟，王 源，张清华，章征林，黄肖迪

(解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007)

冲击荷载作用下泄爆板破坏冲量计算与模拟

由泽伟，王 源，张清华，章征林，黄肖迪

(解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007)

针对工业厂房中的泄爆板在爆炸荷载作用时的破坏问题，根据双向板塑性铰线破坏理论，对其破坏机理进行理论分析。提出了泄爆板的冲量破坏准则，并推导破坏冲量的计算公式；运用ANSYS/LS-DYNA进行数值模拟，与理论结果进行对比，两者吻合较好，证明可以用冲量衡量泄爆板的破坏。分析了影响泄爆板泄爆能力的因素：抗折强度与板的厚度是主要影响因素，而弹性模量及泊松比对破坏冲量的影响相对较小，提出了工业生产中提升泄爆板泄爆能力的方法。

泄爆板；破坏冲量；冲击荷载；塑性铰线；泄爆能力

泄爆板被广泛应用于具有爆炸危险的工业厂房中,在发生爆炸时，泄爆板在较小冲击荷载作用下发生破裂，达到泄压的效果，且破片无棱角，对人的危害较小，因此通常用泄爆板代替厂房中的砖砌墙。与其它泄爆手段相比，泄爆板成本非常低，适合工业上大规模生产。研究泄爆板的破坏机理，探究影响泄爆能力的因素，对工业生产上具有重要指导意义。

对燃气爆炸过程中冲击荷载的作用机理，国内外进行了很多的实验和理论研究，包含建筑物内部超压的产生[1-2]、经验公式的推导和验证[3-4]，泄爆能力的影响因素等[5-6]。高康华等[7]研究了泄压口安装泄爆板时，泄爆板开启或破坏对泄爆能力的影响，建立了各类泄爆板运动方程。针对塑性板的破坏，何建等[8]采用能量守恒原理,将短时间内冲击波对板的作用按冲量来考虑，得到四边固支的矩形钢板在空爆载荷作用下的挠曲线方程。韩永利等[9]根据普通双向板的塑性铰线理论对四边固支墙体进行抗爆计算。Suhubak等[10-12]采用不同方法计算了双向加筋板的动响应。吴桂英等[13-14]用数值模拟的方式分析弹塑性方板在冲击载荷作用下动力响应的反直观行为。前人的研究缺少对板破坏荷载的定量计算，无法对泄爆板的泄爆能力的判定提供理论支持。

以双向板塑性铰线破坏理论为基础，认为由于作用时间很短，在冲击荷载作用下使板破坏的冲量等于极限静荷载使板破坏的冲量，得到泄爆板破坏冲量的计算公式，并通过数值模拟进行验证。

1 理论计算

1.1 硅酸钙泄爆板主要特性

工业上常用泄爆板主要一般采用120 mm×60 mm×6 mm的双层硅酸钙板，两块泄爆板按照安装要求，以铆钉固定在龙骨框架上，龙骨框架棱宽5 mm，高10 mm，如图1所示。

图1 泄爆板示意图Fig.1 Schematic of the vent panel

生产工艺对硅酸钙板的性质有较大影响，主要参数如表1。

表1 硅酸钙板特性Tab.1 The features of calcium silicate board

工业上将材料受弯曲负荷作用而破坏时的极限应力称为抗折强度。

1.2 模型建立

在冲击荷载作用在泄爆板上时，冲击波传播速度远大于板破裂时产生破片的速度，可以认为冲击荷载是使两层板破裂的因素，第一层板破裂对另一层板无影响，即仅考虑单层板的情况。

根据塑性铰线破坏理论建立计算模型，如图2所示。板四边固支，长为a，宽为b，厚度为h，在冲击荷载作用下，沿图1示塑形铰线破坏，x为图示铰点至板短边边界的距离，板的极限应力为σ，板的极限弯矩为Ms，密度为ρ。

图2 板破坏示意图Fig.2 Schematic of the destroy

模型的建立基于以下假设：

(1) 通过铆钉固定四边，板在边界无法发生位移或转动，即可以认为板的四边角位移与线位移都为0，为完全固支条件；

(2) 由于理想刚塑性模型与理想弹塑性模型的极限荷载相同，所以在分析中为简化计算，采用理想刚塑性模型；

(3) 在冲击荷载作用下，板发生小变形,即垂直于板中面方向的线应变忽略不计。

1.3 理论分析

针对应用于工业厂房的泄爆板，主要是求解板在冲击荷载作用下，发生破坏时对应的时间及超压峰值。板的破坏可以看作力在时间上的积累作用，即冲量的作用。静力加载过程中，未达到极限荷载时，板正常工作。而在荷载达到极限荷载的瞬间板发生破坏，相当于作用一个等效的破坏冲量。由于破坏瞬间的作用时间很短，可以认为在冲击荷载作用下使板破坏的冲量I静等于极限静荷载使板破坏的冲量I冲击

I冲击=I静

(1)

在冲击荷载作用下

(2)

式中，S为板的面积。

1.4 破坏冲量的计算

对于矩形薄板，极限弯矩

(3a)

在爆炸荷载作用下，材料的性能有明显的变化，主要表现为强度的提高，而变形性能(包括弹性模量、塑性等)基本不变[15]，取平均强度提高系数ξ=1.2，即在计算过程中，将抗拉极限提高20%，则

(3b)

假设板到达极限状态，变为几何可变机构时，中间塑形铰线挠度为1，根据内力功等于外力功的原理，即使板沿塑性铰线变形的能量等于外力做功，可求出极限荷载的上限解。

We=Ms∑θili

(4)

式中：We为外力做功；θi为第i条塑性铰线处的相对转角；l为第i条塑性铰线的长度。

外力功为板破坏时形成的棱锥体积乘以均布荷载，即

(5)

式中，q为均布荷载。

塑形铰线上极限弯矩做功为

(6)

由式(4)、式(5)、式(6)联立解得

(7)

(8)

在静荷载作用时，可以认为板达到极限静荷载的一瞬间板发生破坏，由于破坏的时间很短，I静作用在板上产生初始动能，最终导致破坏，得到

(9)

式中：m为板的质量；v0为板破坏瞬间的初速度。

由此得

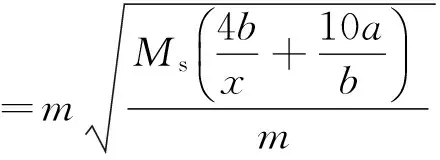
(10)

得到破坏冲量与板各参量之间的关系

(11)

2 数值模拟

运用ANSYS/LS-DYNA有限元程序进行模拟，根据硅酸钙泄爆板各项参数建立有限元模型，在四边龙骨固定处为固支条件。板长1.2 m，宽0.6 m，厚0.006 m，矩形四边0.05 m范围内固支。泄爆板模型采用MAT_PLASTIC_KINEMATIC理想弹塑性材料模型。文献[8]中利用该种材料模型进行板在爆炸荷载作用下的数值模拟，并与实验结果进行对比，取得了较好的效果，说明该模型能较好的模拟板的破坏过程。为表现出泄爆板的破坏过程，采用MAT_ADD_EROSION定义板的失效准则。为提高计算精度，单元类型选用SOLID164号单元，采用映射划分的方式，将板划分12 mm×6 mm×3 mm的立方体单元。材料参数按表1选定。

结构内爆炸产生的荷载可以视为均布荷载，燃气爆炸过程产生的冲击荷载q(t)为时间t的函数，时程曲线，如图3所示。

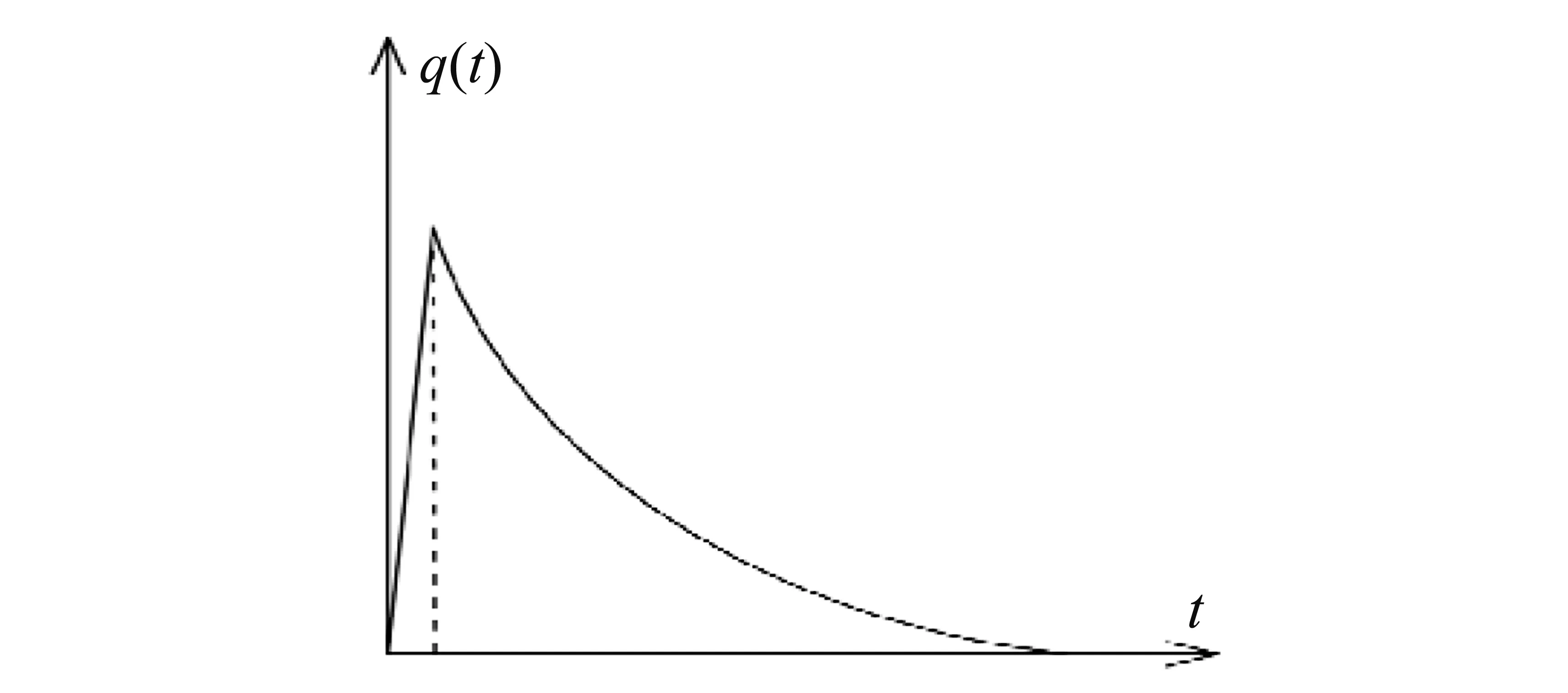
图3 爆炸荷载随时间变化Fig.3 The blast load changing with time

爆炸过程仅考虑升压过程，可将冲击荷载简化为均布线性荷载，q(t)与时间成正比，即

q(t)=kt

(12)

分别取不同升压速度(不同k值)的均布荷载作用在板上，以塑形铰线完全形成为板破坏的标志，确定板破坏时的作用时间及破坏冲量。

3 模拟结果与分析

3.1 破坏冲量模拟结果

模拟破坏过程与假定基本相同，在板中线处最先出现材料失效，然后迅速沿塑性铰线发生破坏，如图4所示。

(a)

(b)

(c)图4 破坏过程效果图Fig.4 Schematic of the destroy process

对于不同k值，得到不同的破坏冲量，如表2所示。

表2 模拟结果Tab.2 Results of simulation

模拟结果比计算结果偏大，原因是在计算过程中，将板简化为刚塑性材料，忽略板的变形，而模拟过程中采用更为贴近实际的理想弹塑性材料，板产生的变形不能忽略，在变形过程中需要更大的冲量,计算结果偏小。但相对误差在10%以内，在工程应用的允许范围内，说明计算结果与实际情况吻合较好，可以用破坏冲量衡量板的泄爆能力。另一方面，计算结果偏小，对结构设计而言偏安全。

3.2 板泄爆能力影响因素分析

当升压速度一定时，由式(11)可知，对泄爆板的泄爆能力起决定性作用的因素是板的厚度h与抗折强度σ，破坏冲量随着h，σ的增加而增加，模拟与计算结果，如图5、图6所示。

图5 破坏冲量随抗折强度变化关系Fig.5 The impulse of damage changing with the strength of extension

图6 破坏冲量随板厚度变化关系Fig.6 The impulse of damage changing with the strength of plate thickness

从图6可知，随着板厚度的增加，破坏冲量与计算结果的误差逐渐增大，主要是因为对抗弯极限的计算是基于板厚度可以忽略的情况，随着厚度增加，由式(3)计算得到的极限弯矩偏小，导致模拟结果比计算结果偏小。

通过式(11)可知材料本身弹性模量与泊松比对泄爆能力的影响不大，破坏冲量与弹性模量与泊松比的变化关系，如图7、图8所示。

从图7可知，泊松比对破坏冲量基本没有影响。从图8可知，弹性模量对破坏冲量有一定影响，但随着弹性模量的增大，误差减小。原因是计算基于小变形的基本假定，当弹性模量较小时，板产生较大的挠度，在变形过程中需要更大的能量，导致计算误差偏大。本文中的理论计算对于大变形与非线性的情况并不适用。在实际生产中，泄爆板的弹性模量一般都大于5 MPa，因此针对泄爆板而言，可以认为弹性模量对泄爆能力影响较小，可忽略大变形与非线性的情况。

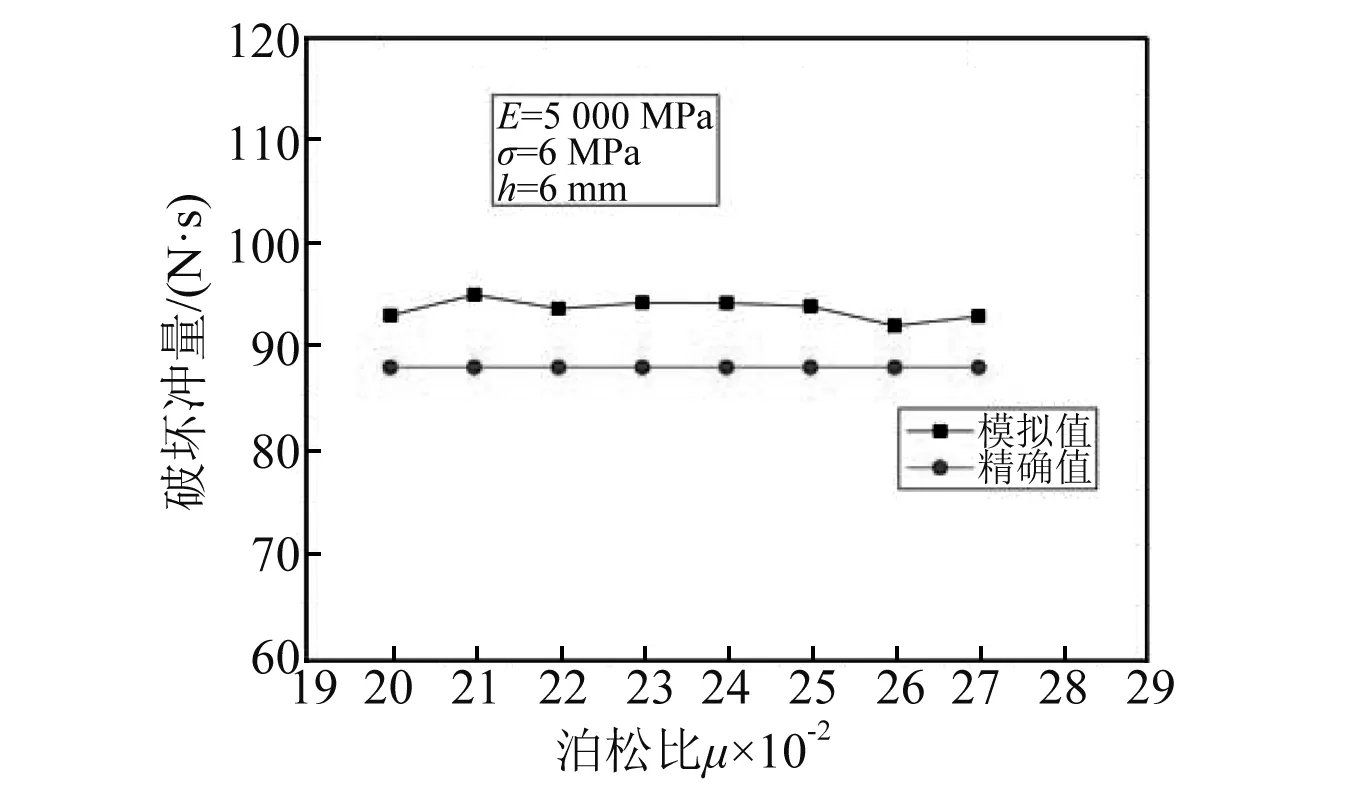
图7 破坏冲量泊松比变化关系Fig.7 The impulse of damage changing with the poisson’s ratio

图8 破坏冲量随弹性模量变化关系Fig.8 The impulse of damage changing with the strength of elasticity modulus

4 结 论

(1)提出了针对工业泄爆板的冲量破坏准则，并推导了破坏冲量的计算公式，计算结果与ANSYS/LS-DYNA模拟结果基本吻合，表明用此方法分析泄爆板的破坏是比较合理的，并能满足工程要求。

(2)破坏冲量的计算基于小变形假设，当弹性模量较小时，产生的计算误差偏大。但针对工业泄爆板而言，弹性模量一般满足使板发生小变形的要求，因此不需要考虑大变形及非线性的情况。

(3)泊松比对板的破坏影响不大,而弹性模量对板的破坏冲量有一定影响，随着弹性模量的增大，这种影响可以逐渐忽略。抗折强度与厚度是影响板破坏的主要因素，在不影响板的构造要求时，通过降低板的抗折强度及减小板厚度，能够有效提高泄爆板的泄爆能力。

[1] COOPER M G, FAIRWEATHER M, TITE J P. On the mechanisms of pressure generation in vented explosions.[J].Combustionand Flame, 1986,65:1-14.

[2] PONIZY B, LEYER J C. Flame dynamics in a vented vessel connected to a duct:1.Mechanism of vessel-duct interaction [J].Combustion and Flame,1999,116:259-271.

[3] 师喜林,蒋军成,王志荣,等．甲烷-空气预混气体泄爆过程的实验研究[J].中国安全科学学报,2007,17(12):107-110. SHI Xilin, JIANG Juncheng, WANG Zhirong, et al. Experimental study on the venting process of methane-air mixture explosion[J]. China Safety Science Journal,2007,17(2):107-110.

[4] 王博,陈思维.密闭受限空间可燃气体爆炸特性数值模拟研究[J].工业安全与环保,2008,34(2):28-29. WANG Bo，CHEN Siwei．Numerical simulation of explosive characteristics of flammable gas in closed restricted space[J].Industrial Safety and Environmental Protection，2008,34(2):28-29.

[5] 丁云,丁大玉,汤明钧．非理想爆源爆炸波的数值计算.[J].爆炸与冲击,1995,15(4):289-299. DING Yun, DING Dayu, TANG Mingjun．Numerical calculation of blast waves from non-ideal explosion sources[J].Explosion and Shock Waves,1995,15(4):289-299.

[6] 胡俊,浦以康,万士昕,等.柱形容器开口泄爆过程中压力发展特性的实验研究[J].爆炸与冲击,2001,21(1):48-52. HU Jun, PU Yikang, WAN Shixin,et al. Experimental investigations of pressure development during explosion vent from cylindrical vessels[J].Explosion and Shock Waves,2001,21(1):48-52.

[7] 高康华,王明洋,程志军,等.泄爆板开启规律及对室内爆燃压力的影响[J].深圳大学学报(理工版),2011,28(6):529-533. GAO Kanghua，WANG Mingyang，CHENG Zhijun,et al.Opening rules of vent panels and its effect on interior deflagration pressure[J]. Journal of Shenzhen University (Science and Engineering), 2011,28(6):529-533.

[8] 何建,肖玉凤,陈振勇,等.空爆载荷作用下固支矩形钢板的塑性极限变形[J].爆炸与冲击,2001,21(1):48-52. HE Jian, XIAO Yufeng, CHEN Zhenyong, et al. Plastic limited deformation analysis of the clamped rectangular steel plate subjected to air non-contact explosion[J].Explosion and Shock Waves,2001,21(1):48-52.

[9] 韩永利,陈龙珠.利用塑性铰线理论求解墙体抗爆能力[J]工程抗震与加固改造,2009,31(6):108-112. HAN Yongli, CHEN Longzhu. Solution method for anti-blast ability of the wall based on yield line theory[J]. Earthquake Resistant Engineering and Retrofitting,2009,31(6):108-112.

[10] SCHUBAK R B, OLSON M D, ANDERSON D L, Rigid-plastic modeling of blast-loaded stiffened plate-part I:one way stiffened plate[J]. Int J Mech Sci,1993,35:289-306.

[11] SCHUBAK R B, OLSON M D, ANDERSON D L. Rigid-plastic modeling of blast-loaded stiffened plate-part Ⅱ:patial and fixity,rate effects and two way stiffened plate[J]. Int J Mech Sci, 1993,35:307-324.

[12] 张涛,刘土光,周晶晶,等，低速冲击载荷下加筋板弹塑动力响应分析[J].应用力学学报,2004,21(4):28-33. ZHANG Tao, LIU Tuguang, ZHOU Jingjing, et al. Elasto-plastic dynamic response of stiffened plates under low velocity impact load[J]. Chinese Journal of Applied Mechanics,2004,21(4):28-33.

[13] 吴桂英,秦冬祺,杨桂通.冲击载荷作用下弹塑性板的反常动力响应研究[J].爆炸与冲击,2003,23(5):420-424. WU Guiying, QIN Dongqi, YANG Guitong. A study on anomalous response of elasto-plastic plates under impulsive loading[J]. Explosion and Shock Waves,2003,23(5):420-424.

[14] HOULSTON R. Finite strip analysis of plates and stiffened plates subjected to air-blast load[J]. Comput and Struct,1989,32:99-106.

[15] 中华人民共和国建设部.人民防空地下室设计规范：GB 50038—2005[S].国家人民防空办公室，2006.

Simulation and calculation for the destroy impulse of vent panels with impact effect

YOU Zewei, WANG Yuan, ZHANG Qinghua, ZHANG Zhenglin，HUANG Xiaodi

(State Key Laboratory of Disaster Prevention and Mitigation of Explosion and Impact，PLA University of Science and Technology，Nanjing 210007, China)

This work aims to solve the problem of the vent panel’s destroy with blast load. Based on the yield line theory of the two-way four edges fixed panel, the failure mechanism was analyzed. The criteria of impulse failure was pretended and the formula of destroy impulse was derived. Simulation was carried out by ANSYS/LS-DYNA. The results agree to theoretical analysis, which confirm venting capacity of vent panels can be measured by impulse. The factors affecting destroy impulse were analyzed. The strength of extension and thickness is the most important factors; however, the elasticity modulus and Poisson’s ratio have a little effect. The ways of improving venting capacity was offered.

vent panel; destroy impulse; blast load; yield line theory;venting capacity; steel fiber

国家重点基础研究发展计划(973)项目(2010CB732003；2013CB036005)

2016-04-01 修改稿收到日期： 2016-05-09

由泽伟 男，硕士生，1993年生

王源 男，教授，1970年生

TU312+.3

A

10.13465/j.cnki.jvs.2017.12.014