基于P系统优化算法的管内瞬变压力优化研究

高 阳， 冯辅周， 张丽霞， 张红星

(1.装甲兵工程学院 机械工程系，北京 100072； 2.武警警官学院 管理科学与工程系，成都 610213；3.太原卫星发射基地，太原 036304)

基于P系统优化算法的管内瞬变压力优化研究

高 阳1，2， 冯辅周1， 张丽霞1， 张红星3

(1.装甲兵工程学院 机械工程系，北京 100072； 2.武警警官学院 管理科学与工程系，成都 610213；3.太原卫星发射基地，太原 036304)

针对复杂管网系统管内瞬变流计算耗时长，且计算结果占用存储空间严重，导致基于遗传算法的管内瞬变压力优化计算寻优效率极低的问题，对遗传算法进行了自适应改进和基于P系统计算模型的改造，以降低算法在寻优过程中调用瞬变流计算模型的次数。案例计算过程表明，算法改进后得到的P系统优化算法在保证寻优效果的基础上，显著提高了瞬变压力优化计算的寻优效率，使搜索时间相对原遗传算法降低了约80%，因而特别适用于复杂管网系统管内瞬变压力优化计算。

瞬变压力优化；管网系统；遗传算法；P系统优化算法

瞬变流又称为水力过渡过程，是指流体从一种稳定流动状态转变为另一种稳定流动状态过程中的中间过渡非稳定流态[1]，在有压管道中当上述过渡流态表现为流量或压力等流动量的剧烈波动时称之为水锤或水击，严重威胁管系的完全运行[2]。对瞬变流数学模型的求解，目前只能借助数值方法[3]，常用的有特征线法及谱方法等[4-8]，其中尤以特征线法应用最广。对于简单管系结构的瞬变流分析，可以根据选定的数值方法直接编程对瞬变过程进行计算，但是对于如加注系统[9]等复杂的管网系统，通常只能借助瞬变流计算软件[10]。对管内瞬变压力的优化，主要用于削弱管内瞬变强度，实现对管内瞬变流的主动控制[11]，保证管系的安全运行。鉴于瞬变流计算的数值计算特点，瞬变压力优化宜选用群智能优化算法。由于管内压力波速极快，导致瞬变流计算中的时间步长往往取的很小，这就使得对复杂管网的瞬变流计算变得非常耗时，且计算结果也将占用大量的存储空间。相应的优化计算中大部分计算资源和时间都将消耗在对个体好坏的评估上，有时甚至因瞬变流计算软件存储空间受限(如Flowmaster)使优化计算无法继续进行。针对以上问题，本文选用理论和应用均比较成熟的遗传算法进行瞬变压力优化计算，并先后对遗传算法进行自适应改进和基于P系统计算模型的改造，从而形成寻优能力更强、效率更高的适用于复杂管网管内瞬变压力优化的P系统优化算法。

1 优化算法及其改进

1.1 自适应遗传算法

基本遗传算法的原理、方法及参数设置等可参见文献[12]。为了提高遗传算法在管内瞬变压力优化中的寻优效率，在保证寻优效果的基础上，应尽量降低对个体适应度的评估次数。而要降低个体适应度的评估次数，主要可以通过降低种群的规模和新个体产生的概率实现。种群规模的确定通常是半经验性的，而产生新个体的概率主要受算法交叉变异算子的影响。较大的交叉变异概率将使每代中产生更多的新个体，使算法搜索过程更趋随机。基本遗传算法在搜索过程中交叉变异概率是恒定的，然而在算法搜索的不同阶段，对算法交叉变异概率的要求是不同的，在此对交叉变异概率采用以下自适应设置[13]：

(1)

(2)

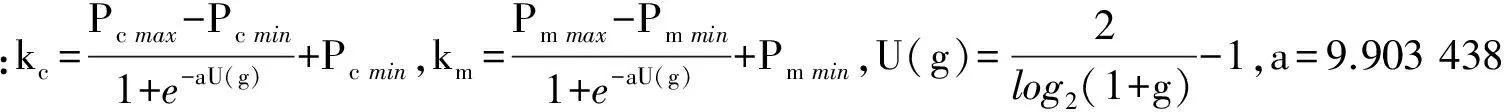
其中:Pc max、Pc min为交叉概率Pc的变化范围；Pm max、Pm min为变异概率Pm的变化范围；fitmax、fitavg为本代最大适应度和平均适应度；g为种群代数。

显然，上述对交叉变异概率的自适应过程，在保证寻优效果的基础上，可以使产生新个体的概率随着种群进化代数的增加而降低，从而减少调用瞬变流计算程序对新个体适应度进行评估的次数，进而提高寻优的效率。

此外，随着搜索过程的进行，算法对个体的选择概率也具有不同要求，同时考虑在进化过程中保留最优个体不被破坏，将排序选择与精英选择方法结合作为个体选择概率的确定方式，其中，各个体的选择概率Ps按如下方式确定：

(3)

式中:k为个体在种群中根据适应度由小到大排序的序号；Ps min为种群中分配的最小选择概率；n为种群规模。

1.2 基于P系统计算的算法改进

上述对遗传算法的自适应改进，可以提高算法在管内瞬变压力优化中的寻优效率，但是对于大型复杂管网，算法的寻优效率仍有待进一步提高。在此，引入细胞型P系统计算模型[14-15]对上述自适应遗传算法做进一步改进。细胞型P系统计算模型利用类膜结构将计算域分割成不同的区域，在不同的区域使用各自的计算规则，而且这些规则离开相应的计算区域将不再起作用，同时，膜的内外侧可以按照一定的规则进行数据对象的交换。由于引入P系统计算模型是为改进自适应遗传算法，因而细胞型P系统计算模型的各区域对象的进化过程仍与自适应遗传算法一致。在此，需要对膜两侧区域对象的传递规则进行说明。

传递规则也称交流规则，是内层膜区域将其中部分对象传递到直接包含该膜的外层区域中，用以替换外层区域较差对象。该规则可表示为

(4)

式中：a为膜i中选定的对象；f为被传递对象需满足的条件，通常被选中对象为膜i区域中的最优对象集。若膜i为表层膜，则直接将膜i区域中的最优对象传递至膜外环境和基本膜区域；否则，需要被传递的对象数量取膜i区域中对象总数的30%左右[16]。以3层膜为例，上述传递过程如图1。

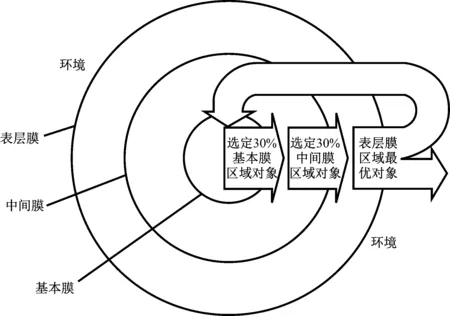
图1 对象传递过程

此外，在优化算法中，为避免在搜索早期算法过早陷入局部最优，增大算法早期区域对象的多样性，让较差对象也有一定机会被传递到外层区域，参与外层区域的进化，因而被传递对象应满足的条件[16]：

(5)

Pi=1-exp((fiti-fitlast max)/g)

式中:fiti为区域i中某对象的适应度；fitlast max为区域i中上次进化的最优对象的适应度；g为进化代数；n为区域中的对象数。

将经P系统计算模型改进后的自适应遗传算法称为P系统优化算法，其算法流程如图2。

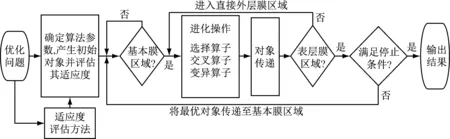
图2 算法流程图

2 瞬变流计算模型

选用文献[17]中案例进行管内瞬变流计算，在长L=600 m、直径D=0.5 m的水平管上游设置液位恒定为Hr=150 m的水源，下游设置阀门与大气连接，如图3所示。其管道波速a=1 200 m/s，管道摩擦因数f=0.018。阀门最初完全打开，其(CdAv)0=0.009 m2，阀门特性参数n=1.5，管内瞬变流由阀门在t0=2.1 s内关闭实现，阀门的关闭规律指数为m。将图3案例在Flowmaster软件中进行瞬态建模，取计算时间步长为0.1 s。现取m=1，在Flowmaster中计算的阀前压力波动情况如图4，考虑单位换算，该计算结果与文献[17]中对应模型设置的计算结果一致。

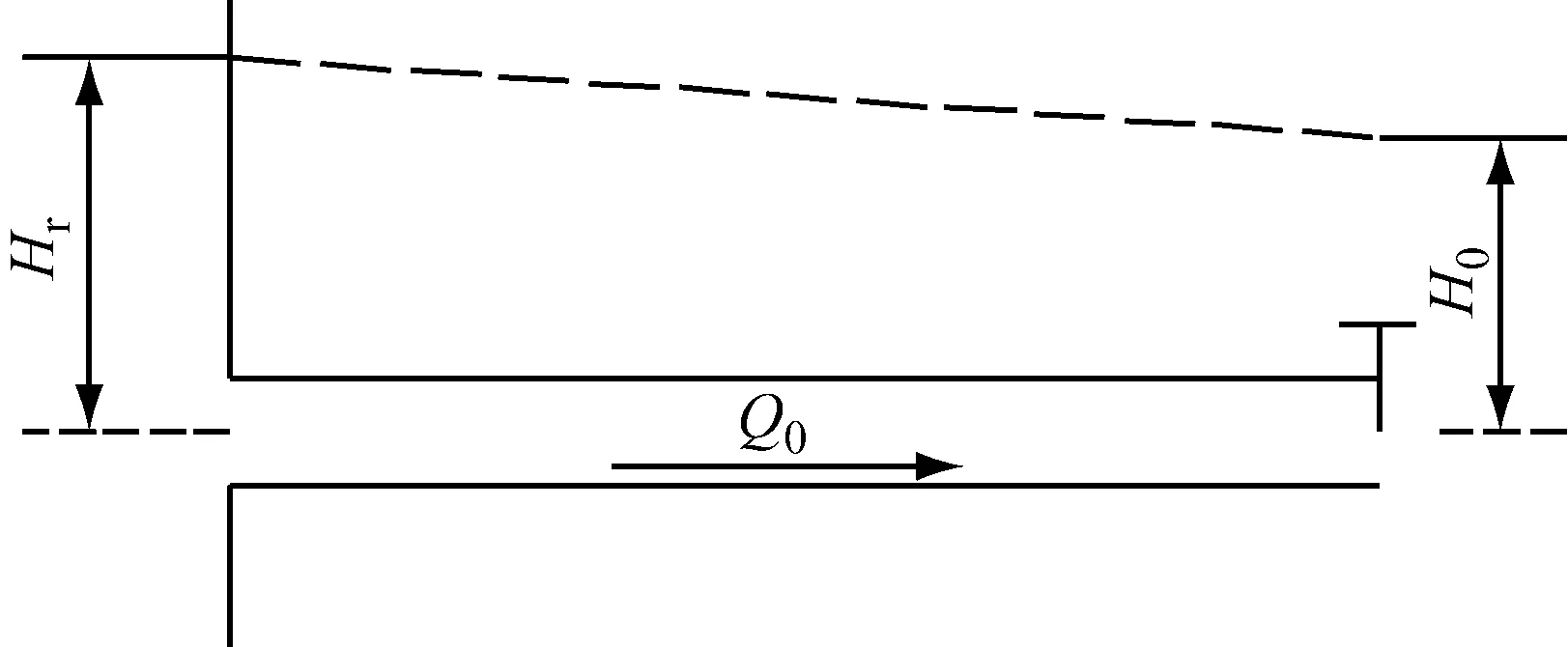
图3 简单管物理模型

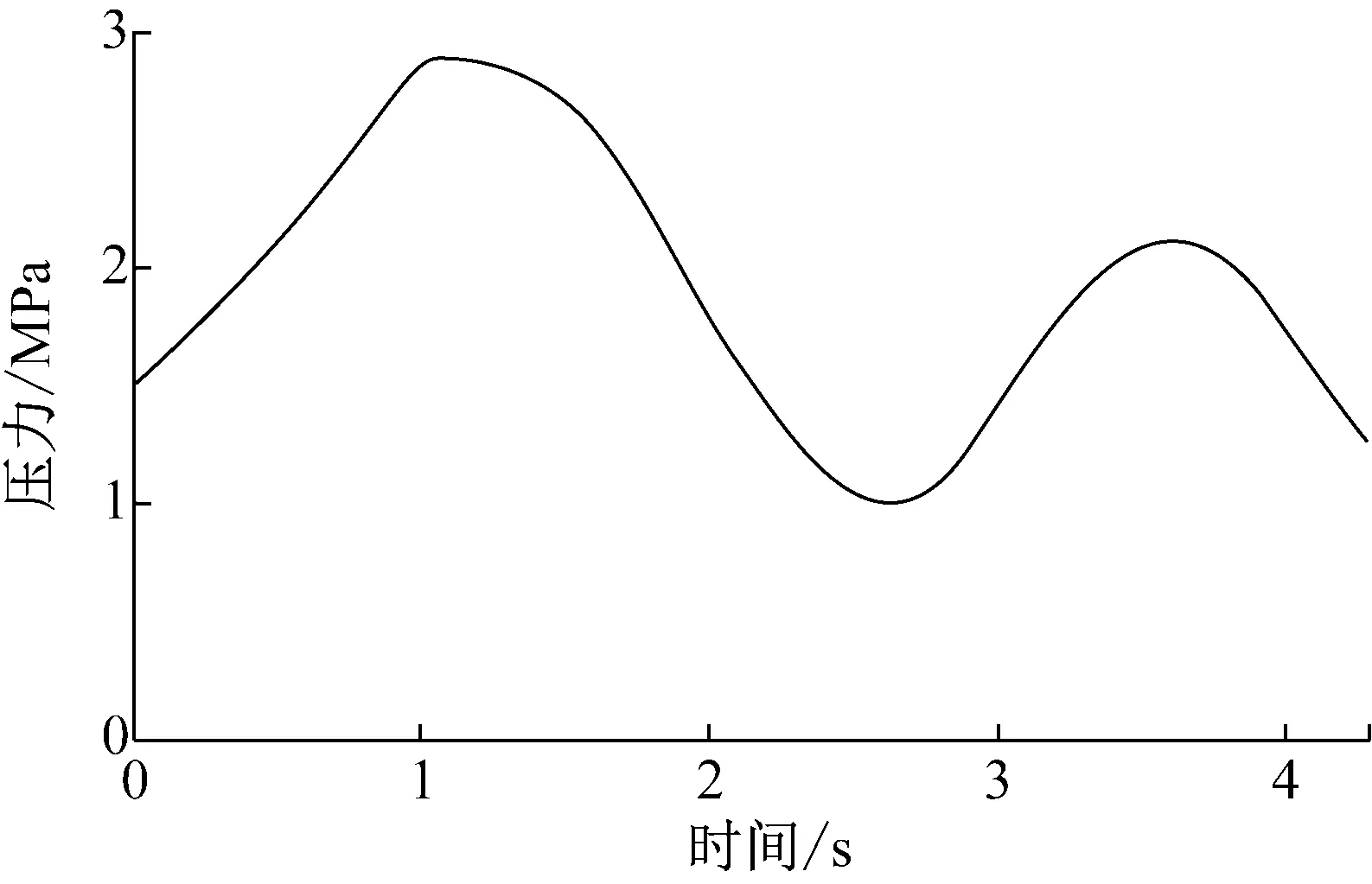
图4 阀前压力波动情况

3 计算结果分析

对于上节的瞬变流计算模型，要做的优化问题为：在(0,10)中对m取合适的值，使阀前压力峰值最低。在此，利用节1中的优化算法解决上述优化问题，以检验算法改进后对瞬变压力优化的优化效率。选用C#进行优化算法的编制，在寻优过程中，算法将调用Flowmaster中的瞬变流计算模型对个体的适应度进行评估，同时将寻优的过程和结果利用Matlab的绘图模块进行绘制，软件间的耦合关系如图5。所有算法均采用实数编码，种群规模均为30，均进化50代，且个体的适应度由阀前压力峰值的倒数进行评估。

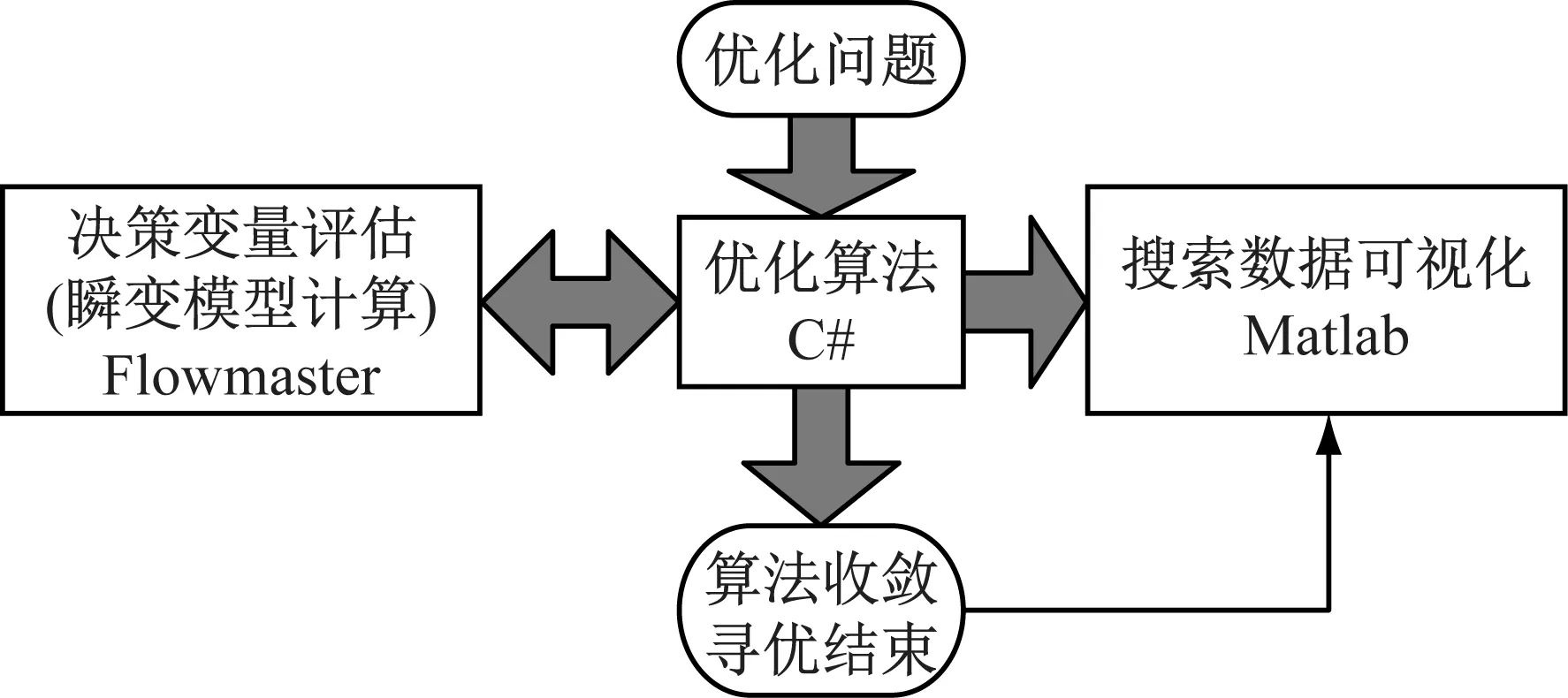
图5 各软件的耦合关系

3.1 自适应遗传算法的计算结果

分别利用基本遗传算法和自适应遗传算法进行管内瞬变压力优化，算法参数设置如表1，优化过程如图6和图7。对比两图可见，经过自适应改进后的遗传算法具有更好的寻优效果和更高的寻优效率。对比图6(c)和图7(c)可知，后者随着种群的进化，每代计算的耗时总体上均有所降低，而且进化50代后的总计算耗时不到前者的1/3，极大地节约了计算资源和时间。根据1.1节可知，自适应遗传算法寻优效率的提高得益于算法交叉变异概率随着种群进化过程的自适应调整。

表1 算法参数设置情况

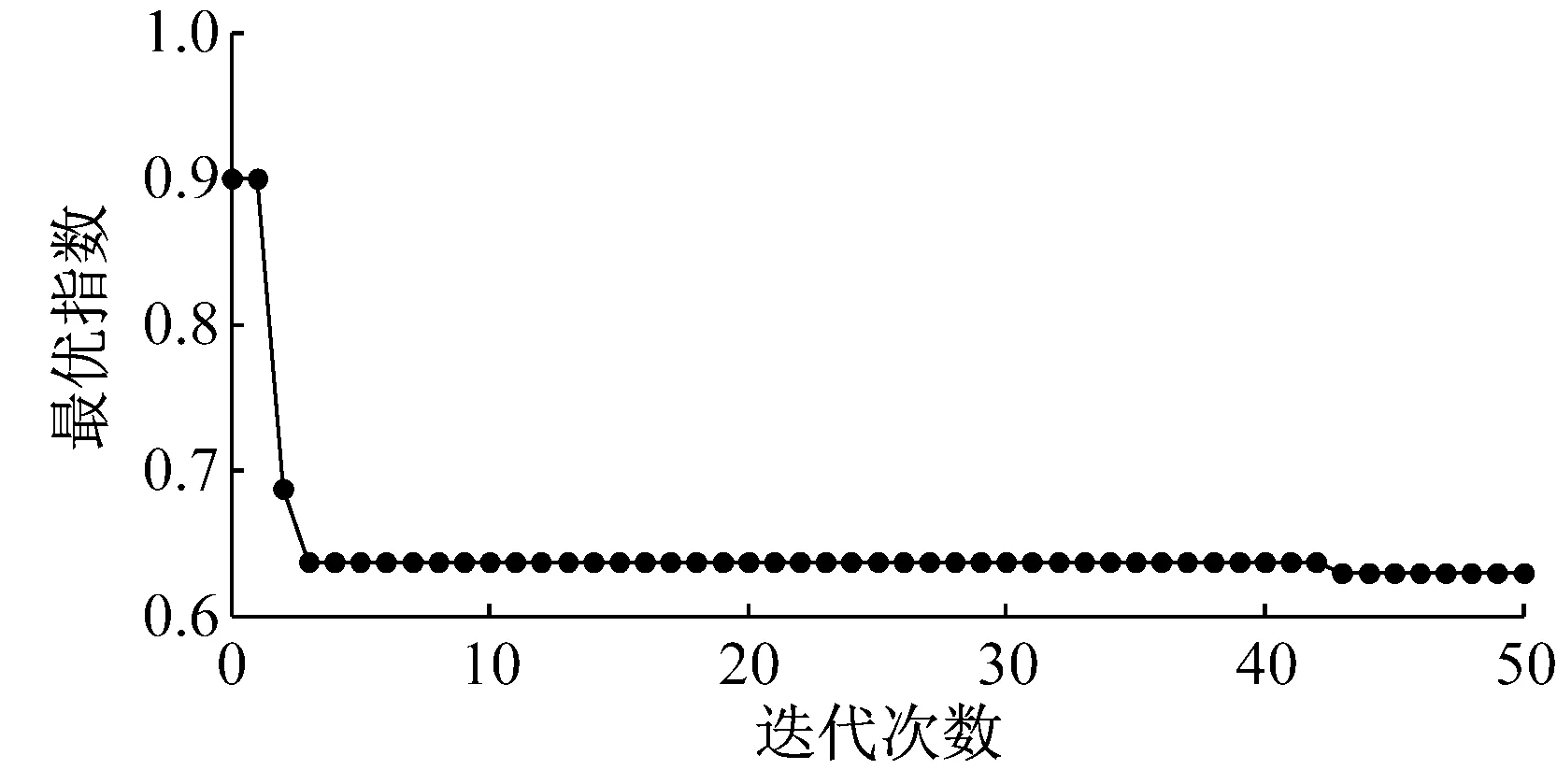
(a) 最优关闭规律指数搜索过程

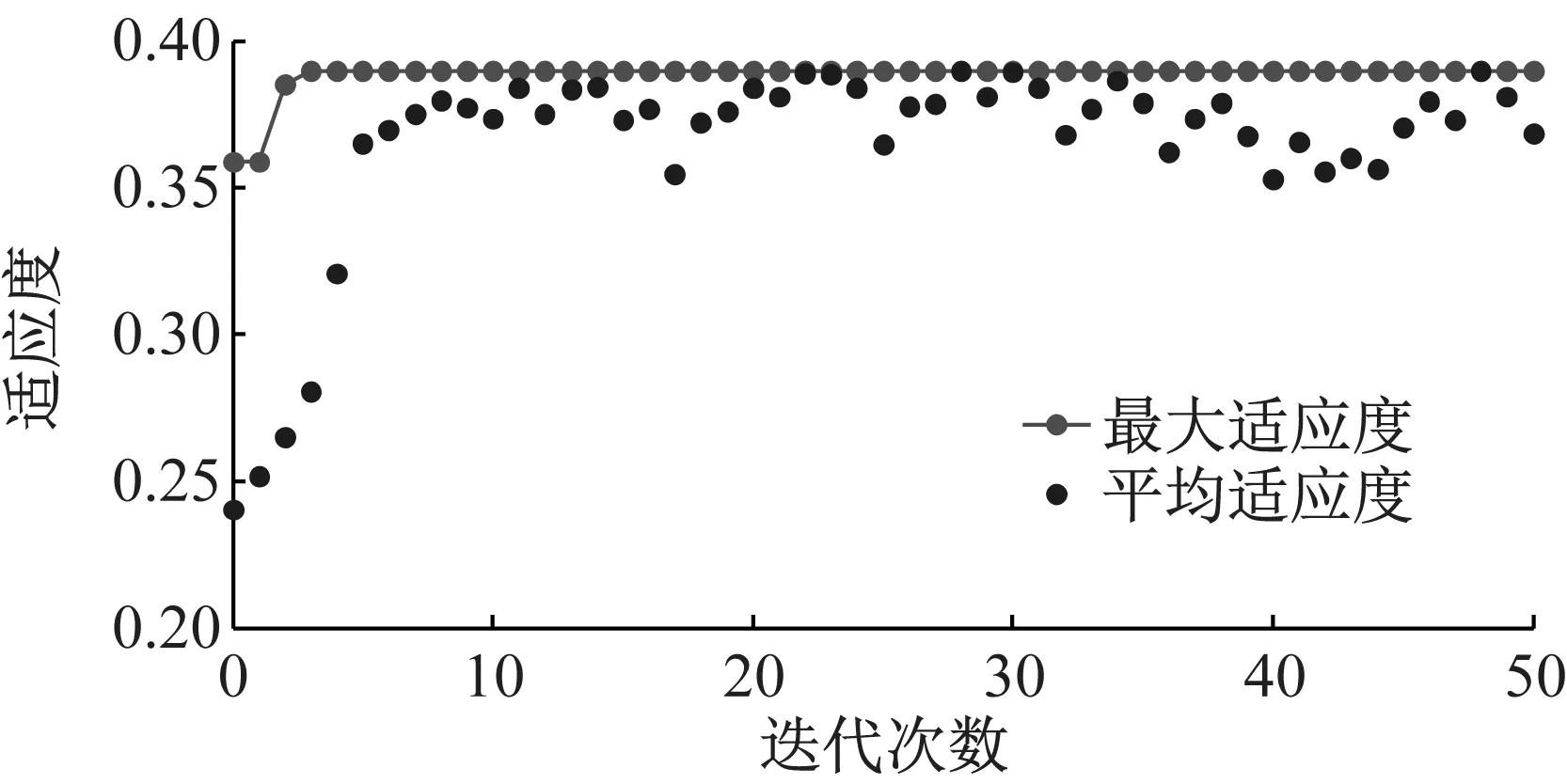
(b) 种群最大适应度和平均适应度情况

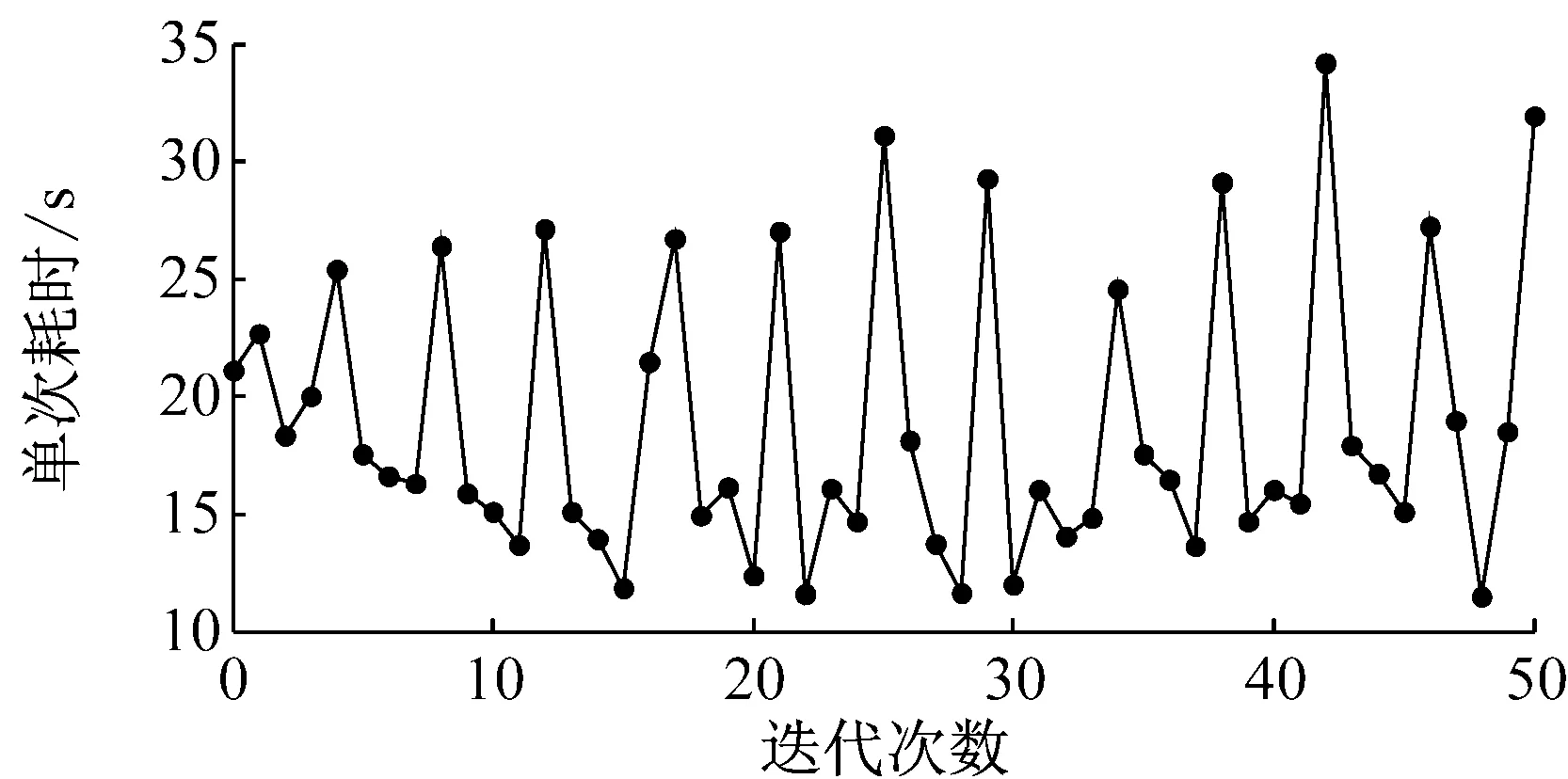
(c) 算法耗时情况

3.2 P系统优化算法的计算结果

利用P系统优化算法进行管内瞬变压力优化，采用图1的3层膜结构，其中表层膜区域、中间膜区域及基本膜区域分配的个体数量分别为16个、9个及5个，优化过程如图8，将其与图7对比可见，P系统优化算法可以进一步提高算法的寻优效果和效率，且随着种群的进化，每代的计算时间逐渐稳定在较低的水平，而其进化50代所耗时间相对自适应遗传算法又降低了约1/3，从而进一步地节约了计算资源和时间。对比图8(c)和图6(c)发现，前者计算总耗时相对后者减少了约80%。

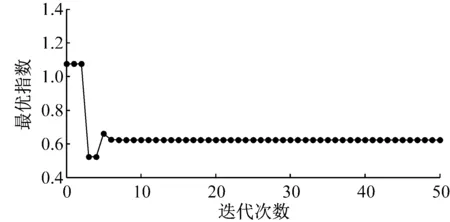
(a) 最优关闭规律指数搜索过程

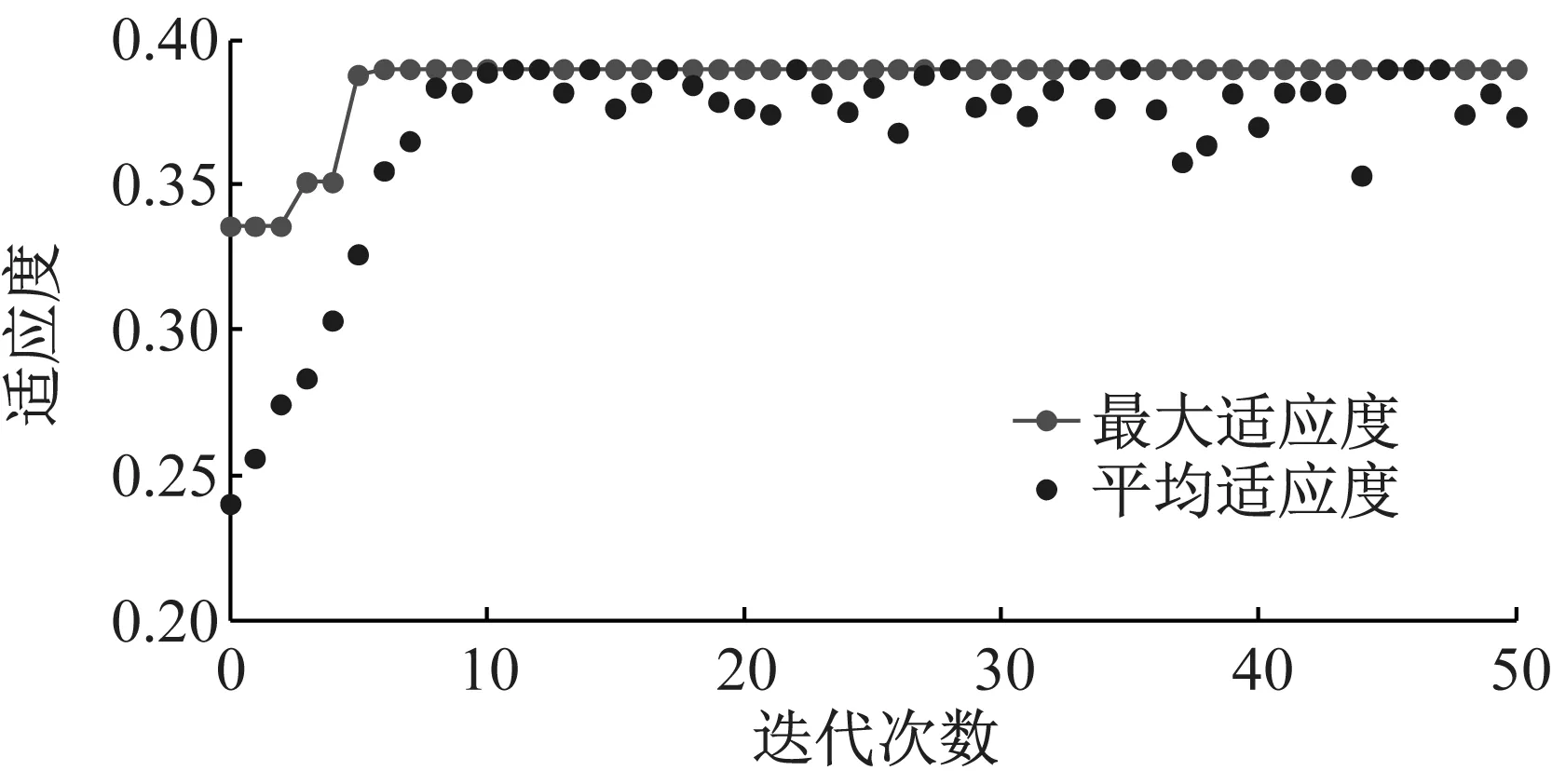
(b) 种群最大适应度和平均适应度情况

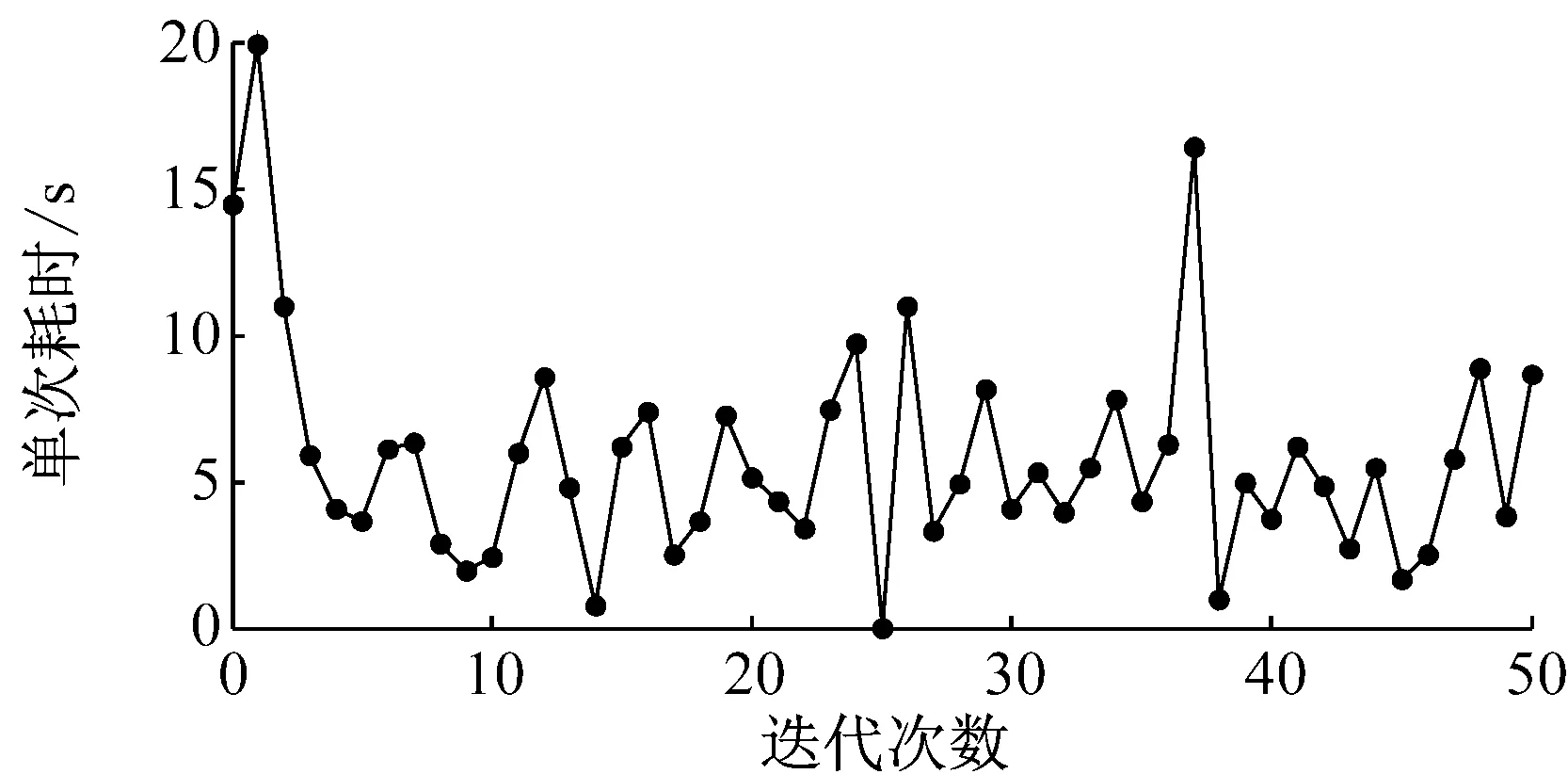
(c) 算法耗时情况

分析造成上述现象的原因可知，P系统计算模型将自适应遗传算法的种群数量分配给不同的膜区域，通常由基本膜区域向表层膜区域逐渐递增，且相同个体可以在不同区域中同时出现。种群每进化一代，P系统优化算法从内层膜向外层膜实施一次由粗至精的搜索过程，内层膜个体数量较少，因而实现的是对最优解的粗略搜索，而外层膜个体数量较多，且包含其直接包含的内层膜的较优个体，因而实现的是较精细的搜索。因此，P系统优化算法每进化一代，相当于自适应遗传算法进化三代。值得特别注意的是，由于种群数量被分配给不同的区域，各区域的进化算子只能在自己的区域中实施，而不能跨区操作，这将进一步减少遗传算法核心操作交叉算子的实施频率，因而可以减少对个体适应度的评估次数，从而达到进一步降低算法的计算时间和占用资源的目的。寻优前后的阀门关闭规律及相应的阀前压力波动情况如图 9，从中可见，经P系统优化算法找到的最优关阀规律较显著地降低了阀前压力峰值。

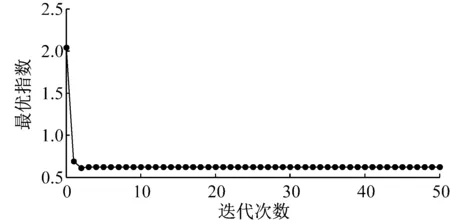
(a) 最优关闭规律指数搜索过程

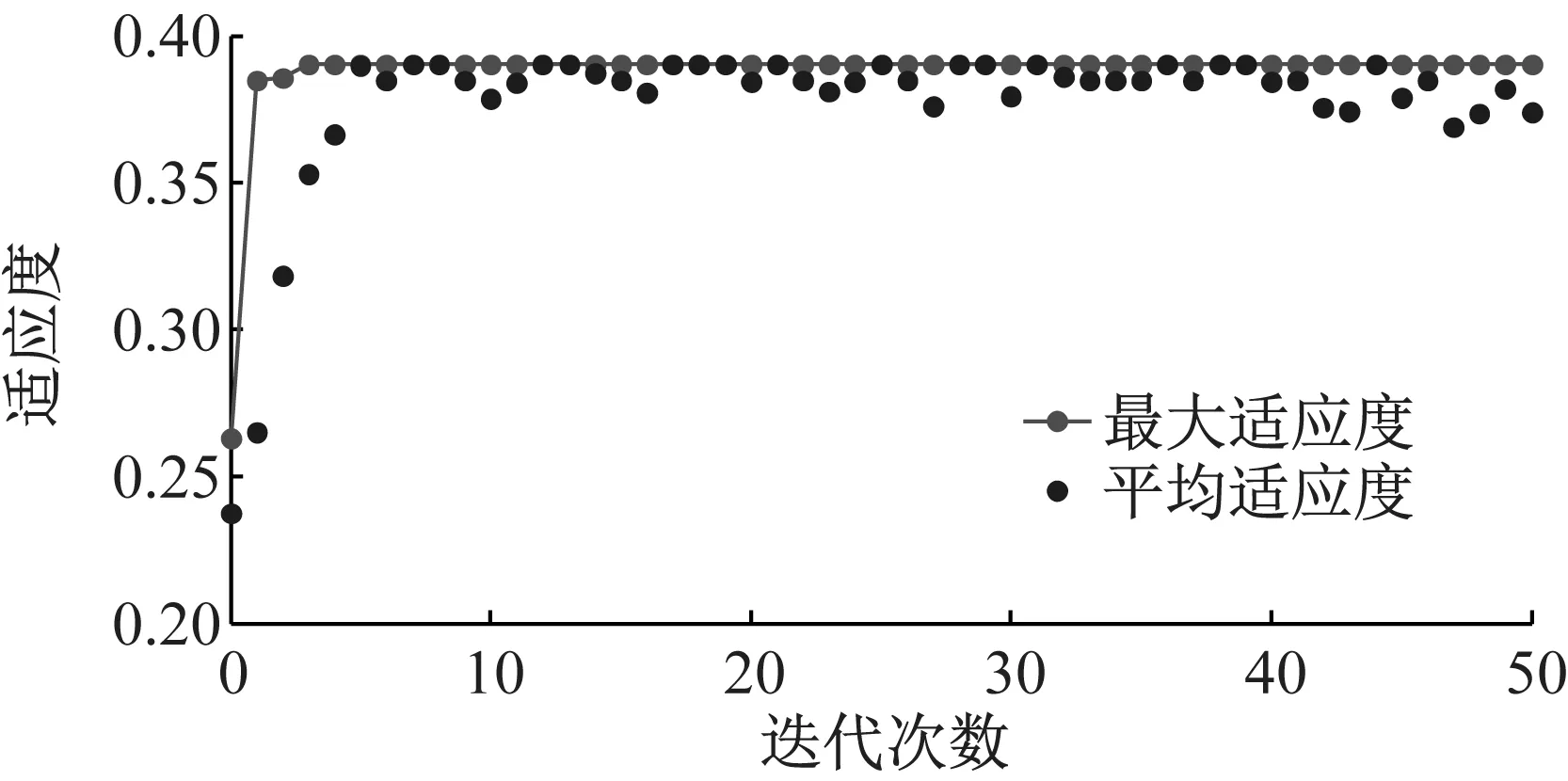
(b) 种群最大适应度和平均适应度情况

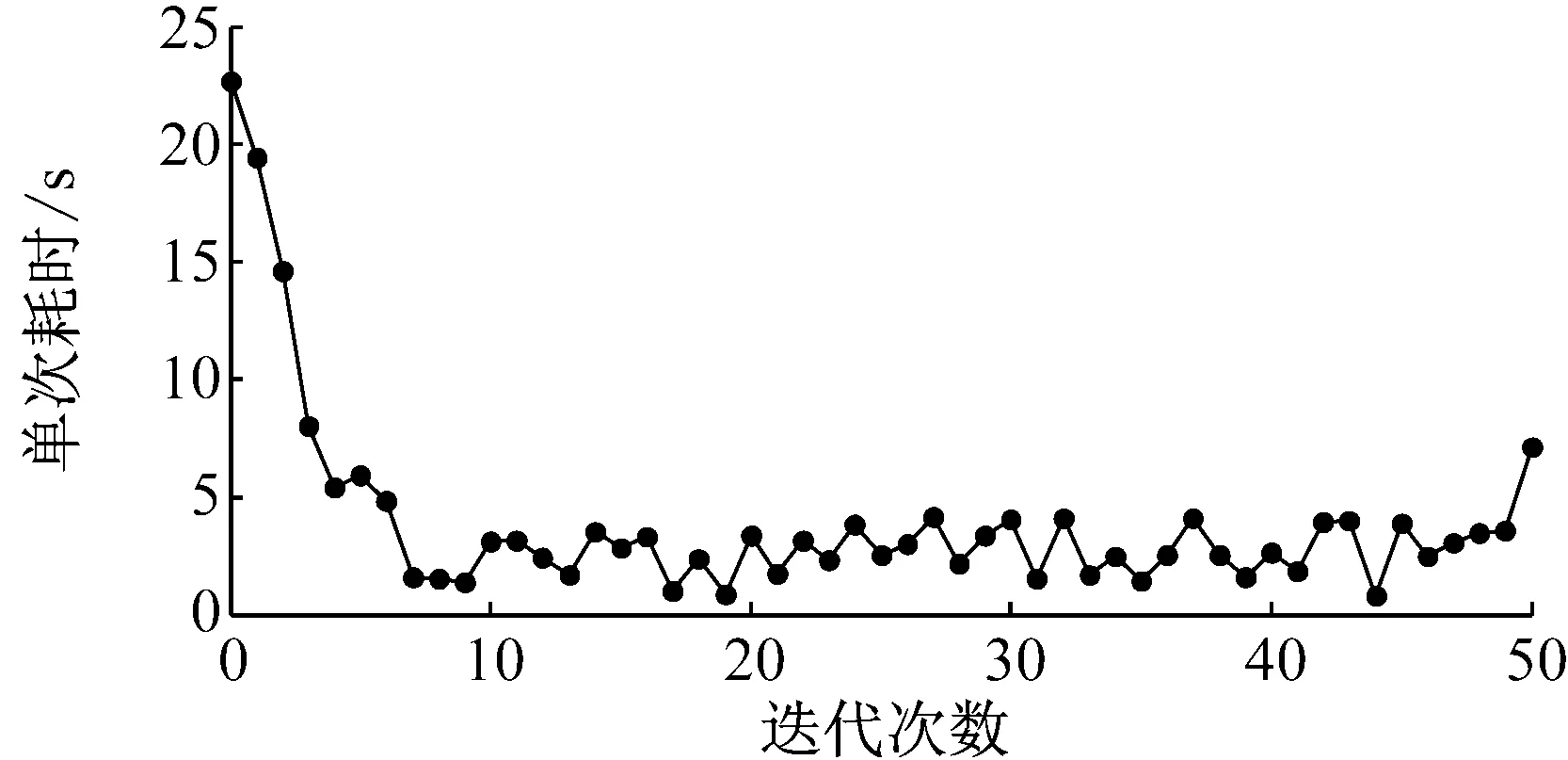
(c) 算法耗时情况

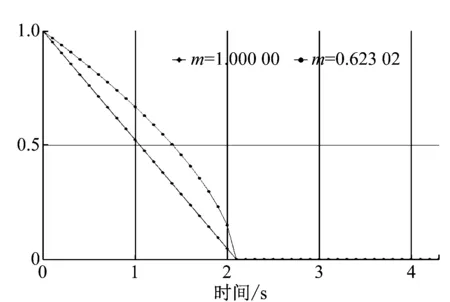
(a) 优化前后阀门关闭规律

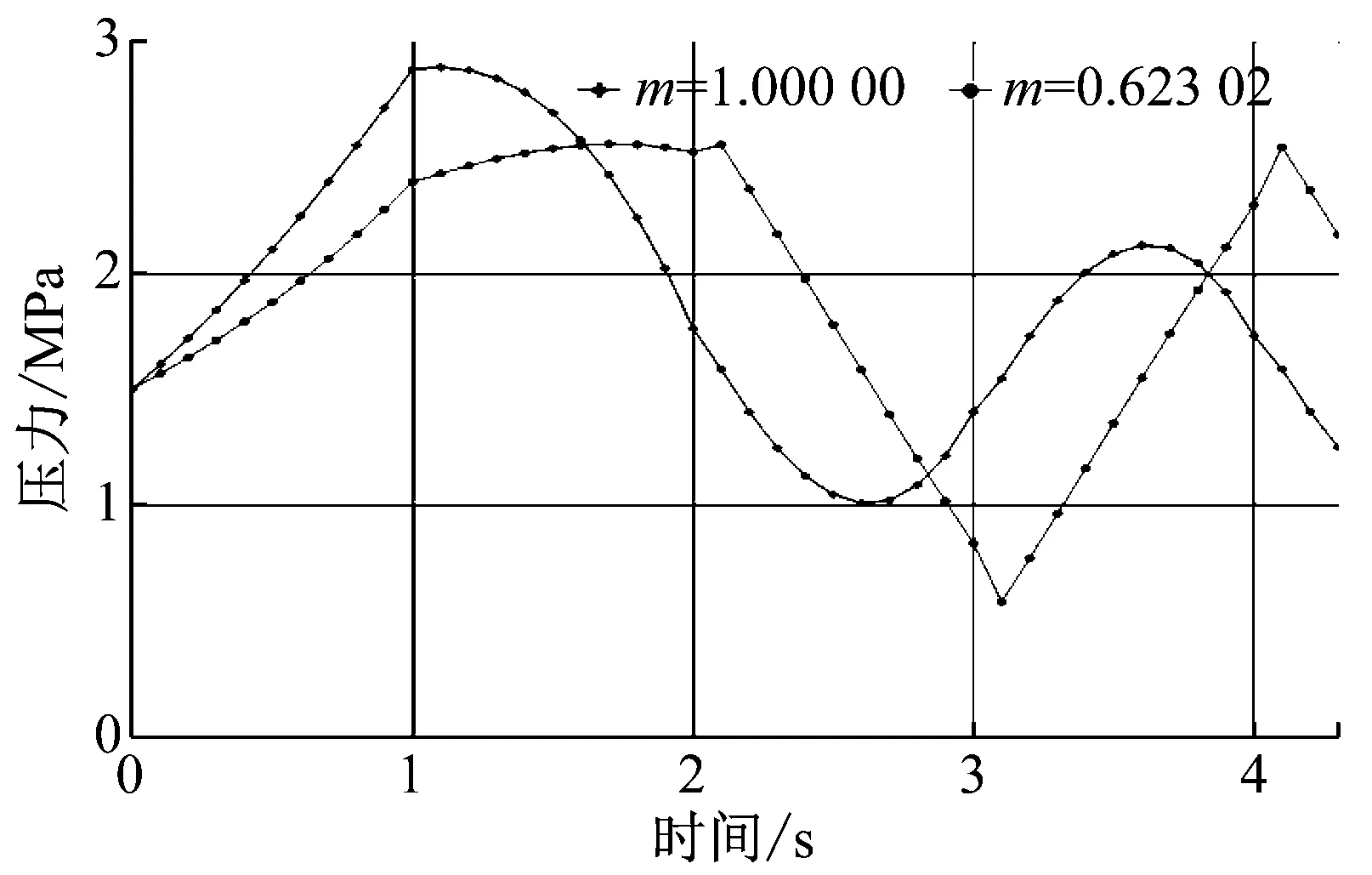
(b) 优化前后阀前压力波动情况

4 总 结

鉴于管内瞬变流计算，特别是复杂管网系统的管内瞬变流计算十分耗时，且计算结果严重占用存储空间，导致基于遗传算法的管内瞬变压力优化计算的大部分时间和资源都消耗在了对个体好坏的评估上，甚至造成寻优工作无法进行，严重制约了算法的寻优效率和寻优效果。针对以上问题，本文先后对遗传算法进行自适应改进和基于P系统计算模型的改造，形成P系统优化算法，并利用该算法调用Flowmaster建立的管内瞬变流计算模型进行管内瞬变压力优化计算，结果表明，P系统优化算法在保证寻优效果的基础上具有更高的寻优效率，因而特别适合复杂管网系统的管内瞬变压力优化计算。

[1] 陈家远. 水力过渡过程的数学模拟及控制[M]. 成都: 四川大学出版社, 2008.

[2] 巴鹏, 邹长星, 陈卫丹. 截止阀启闭时流动特征的动态数值模拟[J]. 振动与冲击, 2010, 29(10): 157-161.

BA Peng, ZOU Changxing, CHEN Weidan. Dynamic numerical simulation of flow features during stop-valve’s opening or closing[J]. Journal of Vibration and Shock, 2010, 29(10): 157-161.

[3] CHAUDHRY M H. Applied hydraulic transients[M]. New York: Springer, 2014.

[4] 耿艳芬, 王志力, 金生. 基于有限体积水锤方程的Godunov格式离散[J]. 计算力学学报, 2007, 24(4): 513-518.

GENG Yanfen, WANG Zhili, JIN Sheng. A godunov method for water hammer problem based on finite volume method[J]. Chinese Journal of Computational Mechanics, 2007, 24(4): 513-518.

[5] 法特. 基于高阶有限差分法的管道瞬态特性研究[D]. 武汉: 华中科技大学, 2011.

[6] 陈宏玉, 刘红军, 陈建华,等. Chebyshev超谱粘性法在推进剂供应管路非定常流动分析中的应用[J]. 推进技术, 2012, 33(5): 804-808.

CHEN Hongyu, LIU Hongjun, CHEN Jianhua, et al. Numerical simulation of fluid transients by Chebyshev super spectral viscosity method for propellant lines[J]. Journal of Propulsion Technology, 2012, 33(5): 804-808.

[7] 曲世琳, 赵洪宾, 伍悦滨. 玻尔兹曼网格方程在长输管道瞬变流中的应用[J]. 南京理工大学学报, 2004, 28(6): 663-667.

QU Shilin, ZHAO Hongbin, WU Yuebin. Lattice boltzmann equation for transient flow of long-distance water supply pipeline[J]. Journal of Nanjing University of Science and Technology, 2004, 28(6): 663-667.

[8] ZECCHIN A C, LAMBERT M F, SIMPSON A R. Inverse laplace transform for transient-state fluid line network simulation[J]. Journal of Engineering Mechanics, 2012(138): 101-115.

[9] 高阳, 冯辅周, 张红星,等. 发射场加注系统瞬变过程及其影响因素研究[J]. 装备学院学报, 2015, 26(4): 89-95.

GAO Yang, FENG Fuzhou, ZHANG Hongxing, et al. Factors on transients and contributory of launch site propellant fueling system[J]. Journal of Equipment Academy, 2015, 26(4): 89-95.

[10] GHIDAOUI M S, ZHAO M, ACINNIS D A, et al. A review of waterhammer theory and practice[J]. Applied Mechanics Reviews, 2005, 58: 49-76.

[11] 宋生奎, 才建. 管道瞬变流动主动控制策略研究综述[J]. 管道技术与设备, 2006(4): 1-4.

SONG Shengkui, CAI Jian. Review on active control strategy of transient flow in pipeline[J]. Pipeline Technique and Equipment, 2006(4): 1-4.

[12] HOLLAND J H. Adaptation in natural and artificial system[M]. Newyork: A Bradford Book, 1992.

[13] 王玉冰, 王锦江, 王颖龙. 一种基于种群熵的自适应遗传算法[J]. 微计算机信息, 2010, 26(1): 32-34.

WANG Yubing, WANG Jinjiang, WANG Yinglong. An colony entropy-based adaptive genetic algorithm[J]. Control & Automation, 2010, 26(1): 32-34.

[14] PAUN G. Membrane computing_an introduction[M]. Berlin Heidelberg: Springer-Verlag, 2002.

[15] 杨世品. P系统优化算法及应用研究[D]. 杭州: 浙江大学, 2012.

[16] 黄亮. 膜计算优化方法研究[D]. 杭州: 浙江大学, 2007.

[17] 高阳, 冯辅周, 张红星. 靶场加注系统中阀门特性对管内瞬变过程的影响[J]. 装甲兵工程学院学报, 2015, 29(2): 81-84.

GAO Yang, FENG Fuzhou, ZHANG Hongxing. Influence of Characteristics of valve in loading system of launch site on hydraulic transients in loading pipes[J]. Journal of Academy of Armored Force Engineering, 2015, 29(2): 81-84.

Hydraulic transient pressure optimization in pipelines based on P-system optimization algorithm

GAO Yang1,2, FENG Fuzhou1, ZHANG Lixia1, ZHANG Hongxing3

(1. Dept. of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China;2． Dept. of Management Science and Engineering, Police Officer College of CAPF, Chengdu 610213, China；3. Taiyuan Launching Base of Satellites, Taiyuan 036304, China)

Aiming at much lower efficiency of hydraulic transient pressure optimization in pipelines based on genetic algorithm(GA) due to serious time-consuming and storage space-occupying for complicated pipe networks’ hydraulic transient flow computation, GA was improved self-adaptively and then modified with the P-system computing model to decease the call number of the hydraulic transient flow computing model in the optimal process of GA. Case study computation process showed that the new algorithm modified with P-system optimization algorithm can significantly improve the optimizing efficiency of hydraulic transient pressure computation in pipes, the searching time is reduced by 80% compared with that of the original GA, so it is specially suitable for complicated pipe networks’ hydraulic transient pressure optimization.

hydraulic transient pressure optimization; pipe network; GA; P-system optimization algorithm

军队科研计划项目(2013WX05)；国家自然科学基金(51205407)

2016-02-19 修改稿收到日期：2016-04-08

高阳 男，博士生，讲师，生于1986年10月

冯辅周 男，博士，教授，生于1971年7月

TV134.1；TH113.1

A

10.13465/j.cnki.jvs.2017.11.029