细编穿刺C/C复合材料热导率数值模拟*

梁 珩，童明波，王玉青，朱书华

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016)

细编穿刺C/C复合材料热导率数值模拟*

梁 珩，童明波，王玉青，朱书华

(南京航空航天大学 飞行器先进设计技术国防重点学科实验室，南京 210016)

根据细编穿刺复合材料的细观和微观结构，分别建立了纤维束和细编穿刺单胞有限元模型。采用周期性非绝热温度边界条件，计算了纤维束和材料整体的等效热导率。计算结果与经验公式比较，具有高度的一致性。在此基础上，进一步研究了纤维体积分数、基体和纤维热导率对材料热导率的影响。结果表明，随着纤维含量的增加，材料两个方向热导率均有不同程度的下降，且差异逐渐减小，且基体对热导率影响作用较大。文中采用的模型和周期性边界条件与理论预期符合较好，为材料热学和热力耦合问题的分析提供了有用参考。

细编穿刺C/C复合材料；有限元；单胞；周期性边界条件；热导率

0 引言

随着现代工业水平、国防技术的快速发展，C/C复合材料因其优异的比刚度、比强度和耐高温性能，而广泛用于航空航天等领域。C/C复合材料也从最初的两向发展为三向、四向等多向编织C/C复合材料，从单一功能材料发展成为多功能材料[1]。复合材料性能的研究也逐渐得到了人们的重视。目前，针对C/C复合材料刚度和强度方面的相关研究较多，对热物理性能的研究则鲜有报道。由于C/C复合材料结构复杂，工作环境温度较高，通过试验获得材料热物理性能费用较高，难度较大。因此，通过有限元分析，对材料的热物理性能进行充分研究，能更好地完成复合材料结构设计工作。

对C/C复合材料的热物理性能，国外已进行了大量的研究[2-4]。Rolfes R和Hammershmidt U[5]对纤维加强复合材料的横向热导率进行了深入研究，提出了多种经验公式，并与试验结果进行了详细比对。Klett J W等[6]建立了一套有限元模型，对影响C/C复合材料的多种因素进行了分析，并准确预测了材料的横向和纵向热导率。Grujicic M等[7]针对不同基体和纤维的三维编织C/C复合材料建立了有限元模型，对其热导率进行了对比分析。结果表明，纤维和基体对材料的热导率都有重要的影响，纤维基体中的孔隙和裂纹会显著下降材料热导率。Hongzhou Li等[8]将周期性边界条件与单胞模型相结合，建立了微观和细观两级单胞模型，对平纹机织复合材料的热导率进行了研究。Jian-Jun Gou等[9]针对三维四向编织复合材料，建立了一套有限元分析方法，对其热导率进行了研究，并与试验结果进行对比分析。

国内关于复合材料热导率的研究资料则相对较少。程伟等[10]采用实验和有限元法，研究了三维四向编织复合材料的等效热物理性能，为后续的理论分析和数值模拟提供了实验参考。Liu[11]和李典森等[12]分别对三维四向和五向编织复合材料的热传导性能进行了研究。然而，上述文献中，对平行于热传导方向的侧面均采用绝热边界条件，限制了胞体之间的热量交换，与实际的情况不太相符。夏彪和卢子兴[13]采用周期性的非绝热温度边界条件和位移边界条件，计算了三维四向和五向编织复合材料的整体等效热传导系数和热膨胀系数，计算结果同已有文献相比，与实验值符合得更好。目前，关于C/C复合材料热导率的研究，已经取得了一定的成果，但仍需深入的对合理的模拟方法进行研究，对指导材料结构与工艺设计，为工程选择复合材料细观结构提供依据，具有非常重要的意义。

本文针对细编穿刺C/C复合材料，分别建立了微观和细观有限元单胞模型，结合周期性边界条件在单胞周围施加非绝热的温度边界条件，对材料的热导率进行了预测。并进一步分析了纤维体积分数、基体和纤维热导率对材料热导率的影响规律。

1 分析方法

1.1 周期性边界条件

在非均质材料的细观有限元分析中，单胞模型被广泛用来计算材料的等效参数[14]。为获得较准确的结果，边界条件选取的合理性至关重要。对于机织复合材料，假设纤维在基体中是均匀且按一定规则分布，则其细观结构具有明显的周期性，宏观结构即可视为相同的单胞结构按照一定的周期性排列而成。本文研究的细编穿刺材料为三向细编穿刺结构，织物的X-Y向为缎布炭纤维叠层，Z向为穿刺的炭纤维束。材料具有明显的平移对称性，选取最小平移对称单位作为该材料的代表性体积单元进行研究，如图1所示。

在平移对称变换下，模型的温度分布也应满足平移对称条件。假设满足平移对称条件的单胞为六面体，如图2所示，0≤x≤a，0≤y≤b，0≤z≤h。周期性温度边界条件的推导过程如下所示：

根据模型的平移对称性，单胞中任意一点P′(x′，y′，z)都可通过其他单胞上的对应点P(x，y，z)在x、y、z方向上经过若干次平移变换得到，即

(1)

其中，i，j，k=0，±1，±2，…表示点P沿着x、y、z轴平移到P′的距离。

对于点P′(x′，y′，z)和P(x，y，z)处的温度场，存在如下关系：

(2)

将式(1)代入式(2)中，得

(3)

根据平移对称性，六面体的三对平行面都可看作是前一个单胞的面沿垂直于该面的坐标轴，通过一次平移变换到后一个单胞中。因此，可得到六面体三队平行面之间的温度约束条件：

(4)

其中，下标x=a和x=0等代表对应面上的普通节点，并不包括单胞边上的点和顶点。

由于单胞的边同时属于两个相邻的平面，则每个边上的点应同时满足两个面的位移约束方程。因此，需重新推导边界条件。给六面体单胞的所有边和顶点进行编号，如图2所示。

为得到单胞各边之间的约束条件，可将单胞的12条边分成3组：平行于x轴的边Ⅸ、Ⅹ、Ⅺ和Ⅻ；平行于y轴的边Ⅴ、Ⅵ、Ⅶ和Ⅷ，以及平行于z轴的边Ⅰ、Ⅱ、Ⅲ和Ⅳ。可看出，不同组的边是相互独立的，每一组内的任意一条边都可由组内其他边通过平移变换转化得到。以边Ⅰ为例，边Ⅱ、Ⅲ、Ⅳ相对于边Ⅰ的变换方式分别为(i=1，j=0，k=0)，(i=1，j=1，k=0)和(i=0，j=1，k=0)。其他两组边具有相似的变换方式。因此，可推导出各组之间的温度约束条件：

(5)

(6)

(7)

以上推导的边同样不包含单胞的顶点，因为任意一个单胞的顶点都同属于3条正相交的边，且任意一个顶点都可由其他顶点通过平移变换得到。例如，顶点7就可通过顶点1通过变换方式(i=1，j=0，k=1)得到，由此可推导出各个顶点之间的温度约束关系：

(8)

1.2 宏观本构关系与等效参数的求解

本文所采用的单胞稳态热传导分析控制方程为

(9)

式中T为温度；λx、λy、λz、λxy等分别为各个方向的热导率。

由控制方程(9)和单胞表面的边界条件，即可求解出单胞的温度分布，x、y、z方向上的热通量与温度梯度的关系，由式(10)给出：

(10)

在边界条件中，引入宏观热通量作为系统的一个独立自由度，则可用参考点上的集中热流来表示宏观热通量，这个宏观热通量与集中热流之间的关系可通过能量公式等效得到。例如，将x方向上的集中热流Qx加载在单胞的相应参考点上，其他的自由度都不约束，则在单位时间内，这个热流产生的能量为

QxΔt=ρcVTx

(11)

式中ρ为材料密度；c为材料比热容；V为单胞体积；Tx为x方向上温度变量。

公式两边同时关于t求导，可得

(12)

又因为

(13)

所以

(14)

(15)

将式(15)代入式(14)中，可得：

(16)

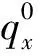
所以，可推出：

(17)

基于上述公式，用Python语言编写了温度周期性边界条件，以显示约束方式施加到模型对应的节点上。在纤维束单胞模型中，施加不同方向的集中热流，计算得到纤维束不同方向的热导率λ1、λ2、λ3。再将这些结果作为细编穿刺单胞模型的材料参数进行输入，计算得到细编穿刺材料各个方向的热导率λx、λy、λz。

2 有限元模型

2.1 纤维束单胞几何模型

在纤维束理论分析中，假设纤维束为纤维在基体中均匀规则分布的单向纤维增强复合材料，纤维体积分数即为其堆积密度。假设纤维在基体中的分布为正六边形分布，如图3所示。据此假设，可建立正六棱柱单胞模型。然而，正六棱柱单胞模型复杂的外形，使得施加边界条件相对困难。所以，将正六棱柱模型拓展为图3中矩形区域作为纤维束单胞，建立厚度方向为单位长度的矩形纤维束单胞模型，并施加周期性温度边界条件。由于不同的纤维体积含量会导致纤维束热传导率的不同，本文分别选取10%～85%纤维体积含量的纤维束进行研究。

(18)

材料采用T300炭纤维，单丝半径r=3.8 μm ，带入式(18)中求得a=16.18 μm，b=9.34 μm。

2.2 细编穿刺单胞几何模型

细编穿刺织物是机织碳布和正交非织造三向织物的组合形式，如图5所示。材料的成型工艺是将炭纤维经整经、穿综、卷纬等工序在织布机上织X-Y向互相交织的平面碳布，再根据织物Z向间距和尺寸，确定Z向钢针矩阵，碳布逐层穿刺，通过加压控制保证碳布层密度和Z向垂直度，达到设计高度后，用炭纤维置换Z向钢针形成织物。

由于复合材料平面结构是由一层经纱和一层纬纱相互交织而成，因此在其面内具有严格的周期性。在厚度方向上，由于细编穿刺材料是由多层压制穿刺而来，假设各层在厚度方向上均匀铺设，忽略表层的影响，则材料内部各层在3个方向上均具有周期性。为了方便有限元模拟，假设Z向纤维束的横截面近似圆形，X-Y向纤维束的横截面近似为椭圆形，且都为密实实体，各向纤维束之间的空隙全部由基体填充。假设X-Y向纤维交织方式均按式(19)给定的余弦公式排列。建立的细编穿刺单胞有限元模型如图6所示。

(19)

经电镜扫描(SEM)分析，得到单胞的尺寸a=b=2.60 mm，h=0.44 mm，X-Y向纤维横截面尺寸w=0.61mm，c=0.20 mm，纤维间距u=v=0.69 mm，Z向纤维横截面半径r=0.29mm，长度与单胞厚度尺寸相同。通过计算得出细编穿刺单胞模型中，纤维束体积含量Vy=48.48%。由于纤维是各向异性材料，而纤维束在碳布中呈交织的弯曲状态，因此需在纤维束中定义局部坐标系，使Z轴始终与纤维束方向平行。

3 结果与分析

3.1 纤维束单胞模型计算结果比较

在纤维束中，轴向的热导率λ3可通过混合法则计算得到：

(20)

式中λfa和λm分别为纤维轴向热导率和基体的热导率。

纤维束横向热导率的情况则相对复杂，为简化计算，假设纤维束为横观各向同性材料，即

(21)

同时为方便有限元模拟，以及计算准则的需要，提出如下假设[5]：

(1)纤维的横截面为圆形；

(2)所有的纤维都完全相同；

(3)纤维均匀的分布在基体中；

(4)基体的热导率是各向同性的，纤维的热导率在面内是各向同性的。

基于上述假设，1982年，Rayleigh[5，15]在三角级数理论基础上，提出了一种经验公式用于计算纤维束横向热导率：

(22)

其中

(23)

S4=0.032 350 24

(24)

Hermans[5，16]在保留了Rayleigh理论的第一要素后，提出一种计算准则用于计算纤维束横向热导率。

(25)

式中λft为纤维横向热导率。

式(25)仅针对纤维与基体为同心圆的复合材料，因此也被称为自洽公式，如图7所示。

计算采用的纤维与基体的参数如表1所示。

表1 碳基体和T300纤维的热导率[17]

不同纤维体积含量的纤维束热导率有限元预测结果如表2所示。有限元预测结果与法则计算结果对比如图8所示。可看出，有限元预测纤维束轴向和横向的热导率结果与法则计算结果高度重合。随着纤维含量的增加，纤维束轴向热导率λ3线性升高。这是因为纤维轴向热导率比基体高，纤维束轴向热量传导主要由纤维承担。而纤维束横向热导率λ1=λ2则逐渐降低，主要因为纤维横向热导率相比基体低得多，使得基体在纤维束横向热量传导中占主导地位，随着纤维体积含量的增加，基体含量减少，使得横向热导率相应降低。70%纤维体积含量的纤维束单胞模型热通量分布图如图9所示。

表2 不同纤维含量体积的纤维束热导率

为进一步验证周期性边界条件的可靠性，参照文献[18]建立沥青基C/C复合材料单胞模型，如图10所示。采用周期性边界条件，忽略界面相的影响，对T300纤维束进行了热导率的模拟。模拟结果如表3所示。由于没有考虑纤维与基体界面相的影响，模拟得到的结果比试验值偏大。综合经验公式和试验对比，认为本文所建模型和周期性温度边界条件可较准确地预测纤维束轴向和横向热导率。

参数FEM/[W/(m·K)]试验结果/[W/(m·K)]误差/%λ1=λ288．4374．3018．98λ3289．61253．8614．08

3.2 纤维含量对细编穿刺复合材料热导率的影响

为研究纤维体积含量对细编穿刺复合材料热导率的影响，采用70%纤维体积含量的纤维束，通过改变纤维束经密和纬密改变纤维体积含量，建立如图11所示的一组模型。

不同纤维体积含量的细编穿刺复合材料的热导率如图12所示。随着纤维束体积含量的增加，单胞面内热导率和Z向热导率均有不同程度的下降。这主要是由于C/C 复合材料作为一元复合材料，其热导率与纤维含量和组元热导率有关，满足混合规则。所以，热导率相对较大的基体体积含量越少，材料的热导率就会越小。其次，由于基体热导率小于纤维轴向热导率却远大于纤维横向热导率。使得复合材料主要沿纤维束轴向方向进行热量的传导，纤维束横向方向则对热量的传导起到一定的阻碍作用。因为细编穿刺复合材料Z向纤维束含量远小于X-Y向纤维束含量，X-Y向纤维束对纵向热量的传导阻碍作用较大。所以，Z向热导率要小于面内热导率。从图12还可看出，随着纤维体束积含量的增加，面内热导率与Z向热导率差距逐渐缩小，这为材料的设计提供一种实用方法，当材料需要在2个方向有不同的热导率比例时，可通过调节材料经密纬密来实现。

图11 纤维束体积含量不同的细编穿刺模型

Fig.11 Fine weave pierced C/C composite of different yarn volume fraction

3.3 细编穿刺复合材料热通量分布

以48.48%纤维束体积含量的单胞为例，在X方向施加集中热流 ，热通量分布图如图13所示。可看出，X向纤维束热通量较大，热通量主要集中在经纱和纬纱的交织处，以及周围的基体。纤维中热通量最大值为1 739 W/m2，周围基体的热通量最大值为1 459 W/m2。

图14为在单胞Z向施加集中热流的热通量分布图。热量主要集中在Z向纤维束及周围的基体上，Z向集中热流下纤维束热通量最大值为26.85 W/m2，基体为25.17 W/m2。

由图13和图14可知，细编穿刺复合材料的热载荷主要由相应方向的纤维束承担，同时纤维束周围基体也承担了较多热载荷。

3.4 参数研究

复合材料的热导率是由纤维、基体和机织方式共同决定的。采用不同的纤维和基体，复合材料的热导率也会有一定的差别。因此，需要对复合材料的敏感性进行研究。通过分别改变纤维丝和基体的热导率，对细编穿刺碳碳复合材料单胞模型进行有限元模拟，模拟结果如图15和图16所示。

图15中，纤维丝热导率不变，将基体的热导率变为原来的1/10为7.04 W/(m·K)。可看出，随着碳基体热导率的减小，单胞整体热导率也较大程度下降。当基体热导率小于纤维热导率时，随着纤维含量的增加，单胞面内和纵向热导率增加。由于细编穿刺复合材料增加了Z向的纤维束，所以纵向热导率与面内热导率相差不多。

图16中，基体和纤维横向热导率保持不变，轴向热导率提高到200 W/(m·K)。由图16可知，随着轴向热导率的增加，单胞整体各个方向的热导率均有不同程度的增加，但增加幅度较小。由于纤维横向热导率依然小于基体热导率，单胞面内热导率依然随纤维含量的增加呈下降趋势。Z向热导率则小幅上扬。

4 结论

(1)本文所采用的周期性边界条件保证了在单元胞体之间的热量交换，与实际情况较为相符，预测结果与经验公式吻合程度较高。为后续复合材料的结构性能研究及优化奠定了一定的研究基础。

(2)针对不同机织密度的单胞进行有限元分析，研究表明，随着纤维含量的增加，材料两个方向热导率均有不同程度的下降，且差异逐渐减小，为材料的设计提供一种实用方法。

(3)针对不同纤维含量的单胞的材料分析表明，材料对基体热导率敏感性较高。当基体热导率大于纤维横向热导率时，材料Z向热导率和面内热导率随着纤维含量的增加而下降，其中面内热导率下降趋势较快。反之，热导率随纤维含量增加呈上升趋势。

[1] 石振海,李克智,李贺军,等.航天器热防护材料研究现状与发展趋势[J].材料导报,2007,21(8):15-18.

[2] Zou M Q,Yu B M,Zhang D M,et al.Study on optimization of transverse thermal conductivities of unidirectional composites [J].Journal of Heat Transfer,2003,125(2):980-987.

[3] Goo N S,Woo K.Measurement and prediction of effective thermal conductivities of woven fabric composites[J].International Journal of Modern Physics B,2003,17(8-9):1808-1813.

[4] Woo K,Goo N S.Thermal conductivity of carbon-phenolic 8-harness satin weave composites[J].Composite Structures,2004,66(1-4):521-526.

[5] Rolfes R,Hammerschmidt U.Transverse thermal conductivity of CFRP laminates: a numerical and experimental validation of approximation formulae[J].Composites Science and Technology,1995,54 (1):45-54.

[7] Klett J W,Edie D D.Flexible towpreg for the fabrication of high thermal conductivity carbon/carbon composites[J].Carbon,1995,33(10):1485-1503.

[6] Grujicic M,Zhao C L,Dusel E C,et al.Computational analysis of the thermal conductivity of the carbon-carbon composite materials[J].Journal of Materials Science,2006,41(24):8244-8256.

[8] Li H Z,Li S G,Wang Y C.Prediction of effective thermal conductivities of woven fabric composites using unit cells at multiple length scales[J].Journal of Materials Research,2011,26(3):384-394.

[9] Gou J J,Zhang H,Dai Y J,et al.Numerical prediction of effective thermal conductivities of 3D four-directional braided composites[J].Composite Structures,2015,125:509-519.

[10] 程伟,赵寿根,刘振国,等.三维四向编织复合材料等效热特性数值分析和试验研究[J].航空学报,2002,23(2):102-105.

[11] Liu Z G,Zhang H G,Lu Z X.Investigation on the thermal conductivity of 3-dimensional and 4-directional braided composites[J].Chinese Journal of Aeronautics,2007,20(4):327-331.

[12] 李典森,卢子兴,刘振国,等.三维五向编织复合材料导热性能的有限元分析[J].航空动力学报,2008,23(8):1455-1460.

[13] 夏彪,卢子兴.三维编织复合材料热物理性能的有限元分析[J].航空学报,2011,32(6):1040-1049.

[14] 潘清.细观力学可视参数化建模及一种新型扩展有限元方法研究[D].南京:南京航空航天大学,2012.

[15] Lord Rayleigh.On the influence of obstacles arranged in rectangular order upon the properties of a medium[J].Phil.Mag,1982,34:481-502.

[16] Hermans J J.The elastic properties of fiber reinforced materials when the fibers are aligned[C]//Proc.Konigl.Nederl.A kad.Weteschappen,1967,B70,l.

[17] 张沫.多向编织复合材料热物理性能研究[D].哈尔滨:哈尔滨工业大学,2008.

[18] 支佳运.沥青基碳/碳复合材料热导率的理论研究[D].北京:华北电力大学,2015.

(编辑：薛永利)

Simulation on effective thermal conductivity of fine weave pierced C/C composite

LIANG Heng，TONG Ming-bo，WANG Yu-qing，ZHU Shu-hua

(Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China)

Based on the meso and micro structures of the fine weave pierced C/C composite,finite element models of a single braiding yarn and C/C composites were established, respectively.By using the periodic non-adiabatic temperature boundary condition, the effective thermal conductivity of yarns and composites were calculated.The calculation results were highly consistent with empirical formula.Furthermore, the law of effective thermal conductivity by material parameters(i.e.fiber volume fraction,fiber and matrix thermal conductivity)was studied. With the increase of the fiber fraction,the transverse and longitudinal effective thermal conductivities decrease with reduced discrepancy.The thermal conductivity of the matrix has much more effects on the global effective thermal conductivity.Based on the FE model and boundary conditions proposed in this paper,the calculation results are in good agreement with the theory, which provides a useful reference for the analysis of thermal and thermo-mechanical coupling.

fine weave pierced C/C composites；FEM；unit cell；periodic boundary condition；thermal conductivity

2016-01-08；

2016-02-14。

国家自然科学基金(11302105)；中国航空科学基金(2014ZF52074)。

梁珩(1989—)，男，博士，研究方向为飞行器结构设计。E-mail： leunghengh@sina.com

童明波，男，教授，研究方向为飞行器结构设计。E-mail：tongw@nuaa.edu.cn

V258

A

1006-2793(2017)03-0364-08

10.7673/j.issn.1006-2793.2017.03.017